Automated Formal Verification of Software Randal E Bryant

Automated Formal Verification of Software Randal E. Bryant Carnegie Mellon University http: //www. cs. cmu. edu/~bryant

The Dream … and the Reality Programs Should be Formally Specified and Proved 1960 s: Logical foundations of programs n Floyd, Hoare, Dijkstra, Scott … 1970 s: Attempts to automate proof process n n Based on automated theorem provers Intensive human effort required, even for small programs 1980 s, 90 s: General disillusionment n n – 2– Hard to fully describe what program should do Software is far to complex to verify completely

Changing Software Environment Early IT Systems n Expert users n Understood and expected failures Modern Environment n More demanding users l Nontechnical people less tolerant of errors n Safety critical systems l Computers control everything from pacemakers to stock exchanges n Hostile operating conditions l Systems under constant attack by malicious forces l Software errors make systems vulnerable – 3–

Use of Formal Verification for Hardware Environment n Higher need for first-time success n Simulation speeds limit amount of testing achievable Equivalence Checkers n Prove that low-level implementation matches high-level description l Routinely performed on all designs Component Verification n n Floating-point units, memory arrays, … Common practice for large manufacturers Model Checking n – 4– Automatically check specific properties of system

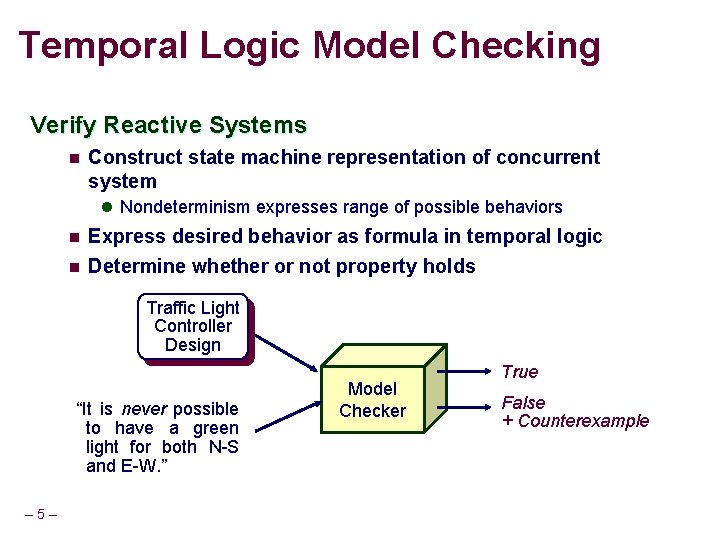
Temporal Logic Model Checking Verify Reactive Systems n Construct state machine representation of concurrent system l Nondeterminism expresses range of possible behaviors n n Express desired behavior as formula in temporal logic Determine whether or not property holds Traffic Light Controller Design “It is never possible to have a green light for both N-S and E-W. ” – 5– Model Checker True False + Counterexample

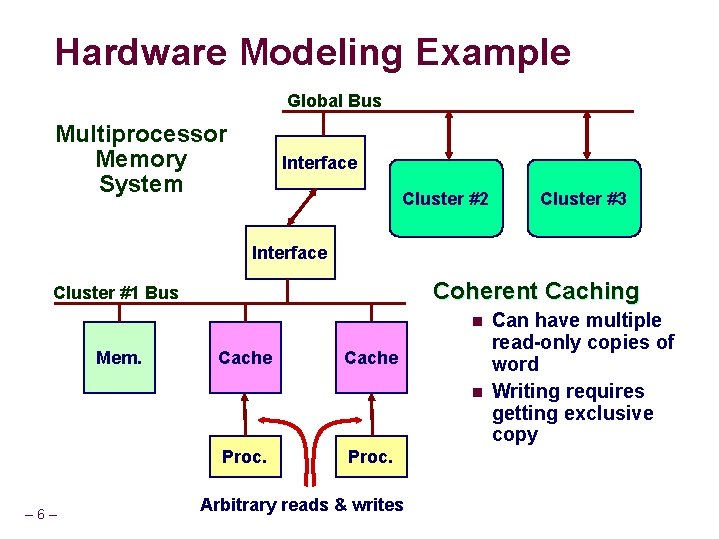
Hardware Modeling Example Global Bus Multiprocessor Memory System Interface Cluster #2 Cluster #3 Interface Coherent Caching Cluster #1 Bus n Mem. Cache n Proc. – 6– Proc. Arbitrary reads & writes Can have multiple read-only copies of word Writing requires getting exclusive copy

Symbolic Model Checking Example n K. Mc. Millan, E. Clarke (CMU) J. Schwalbe (Encore Computer) Encore Gigamax Cache System n n n Distributed memory multiprocessor Cache system to improve access time Complex hardware and synchronization protocol. Verification n n Create “simplified” finite state model of system (109 states!) Verify properties about set of reachable states Bug Detected n n n – 7– Sequence of 13 bus events leading to deadlock With random simulations, would require 2 years to generate failing case. In real system, would yield MTBF < 1 day.

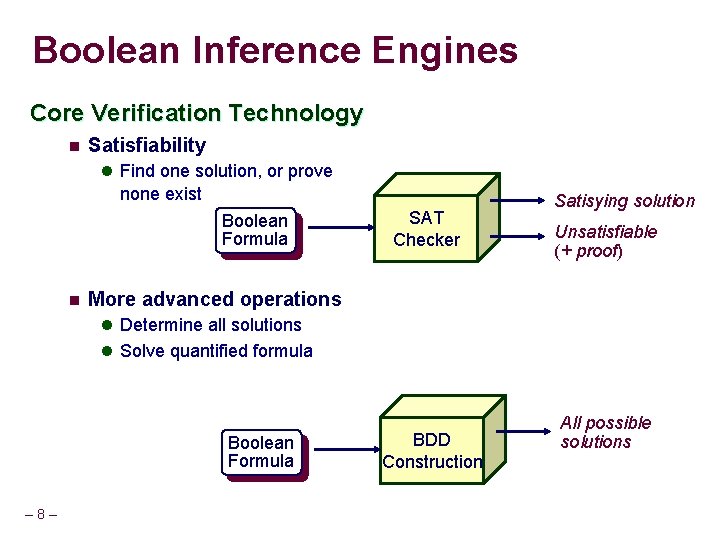
Boolean Inference Engines Core Verification Technology n Satisfiability l Find one solution, or prove none exist Boolean Formula n SAT Checker Satisying solution Unsatisfiable (+ proof) More advanced operations l Determine all solutions l Solve quantified formula Boolean Formula – 8– BDD Construction All possible solutions

Recent Progress in SAT Solving – 9–

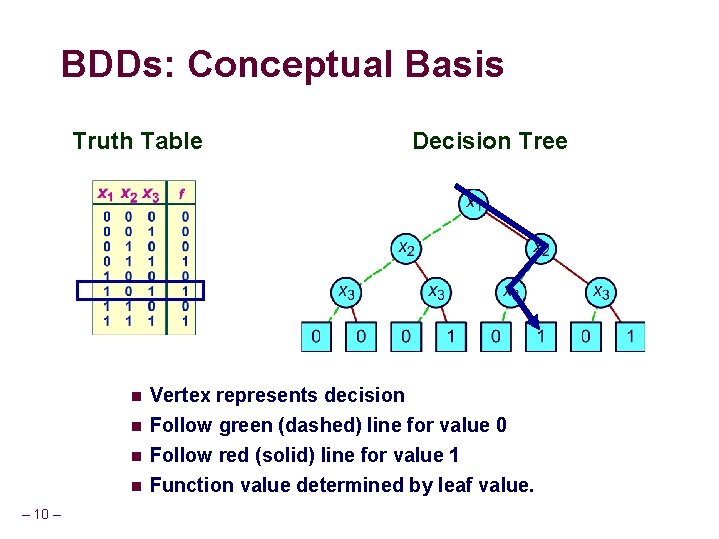
BDDs: Conceptual Basis Truth Table n n – 10 – Decision Tree Vertex represents decision Follow green (dashed) line for value 0 Follow red (solid) line for value 1 Function value determined by leaf value.

Example BDD Initial Graph Reduced Graph (x 1 x 2) x 3 Canonical representation of Boolean function o n For given variable ordering Two functions equivalent if and only if graphs isomorphic l Can be tested in linear time n – 11 – Desirable property: simplest form is canonical.

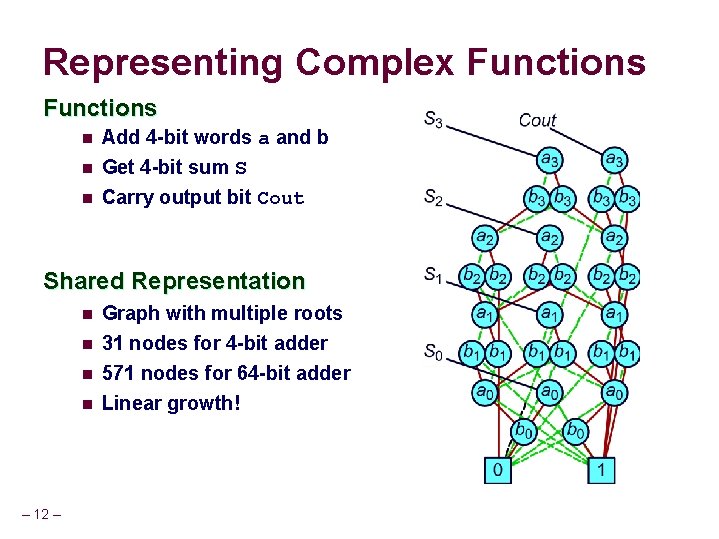
Representing Complex Functions n n n Add 4 -bit words a and b Get 4 -bit sum S Carry output bit Cout Shared Representation n n – 12 – Graph with multiple roots 31 nodes for 4 -bit adder 571 nodes for 64 -bit adder Linear growth!

Model Checking State of Art Symbolic Model Checkers n n Use combinations of SAT checking and BDDs to represent and manipulate sets of possible system states Can verify systems with over 1020 states l Far too large to represent states explicitly Applications n n Standard tool for cache & bus protocol designers Requires sophisticated users l Large companies have own tool and support group l Some commercial versions available – 13 –

Automatic Verification of Software Challenge n Apply techniques devised for verifying hardware to software Strategy n Minimize human effort l Do not expect detailed specifications l Automated inference techniques n Partial verification l Only verify limited properties of system l Example: Program invulnerable to buffer overflow attacks – 14 –

Example: Program Equivalence Checking int abs(int x) { int mask = x>>31; return (x ^ mask) + ~mask + 1; } int test_abs(int x) { return (x < 0) ? -x : x; } Do these functions produce identical results? Strategy n – 15 – Represent and reason about bit-level program behavior

Bit-Level Program Verification x 0 y 0 x 1 y 1 x 2 y 2 x 2 • • abs • • x 31 • • absi • • y 31 x 31 View computer word as 32 separate bit values Each output becomes Boolean function of inputs – 16 – yi

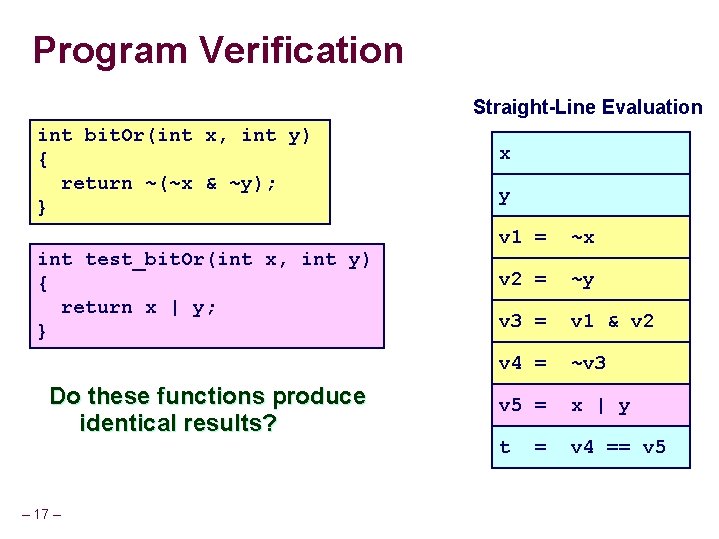
Program Verification Straight-Line Evaluation int bit. Or(int x, int y) { return ~(~x & ~y); } int test_bit. Or(int x, int y) { return x | y; } Do these functions produce identical results? – 17 – x y v 1 = ~x v 2 = ~y v 3 = v 1 & v 2 v 4 = ~v 3 v 5 = x | y t v 4 == v 5 =

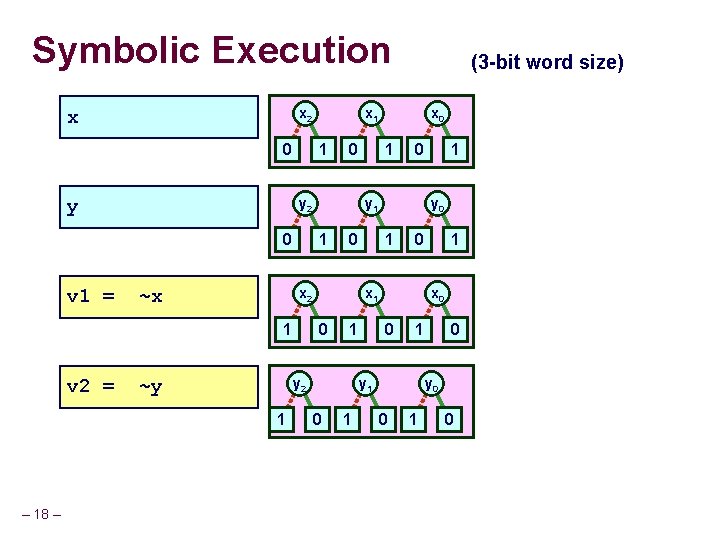
Symbolic Execution x 2 x 0 y v 1 = ~x ~y x 0 1 0 y 1 1 0 x 2 0 1 1 x 0 0 1 y 1 0 1 y 0 x 1 y 2 1 – 18 – 0 y 2 1 v 2 = x 1 1 0 (3 -bit word size) 0 y 0 0 1 0

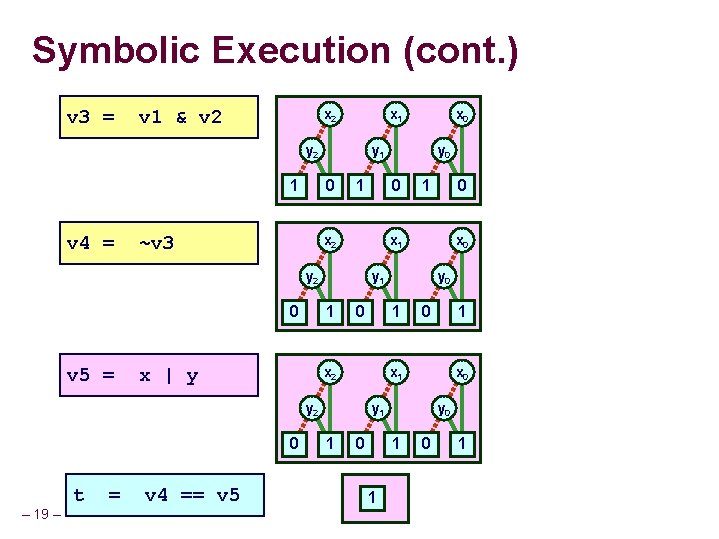
Symbolic Execution (cont. ) v 3 = v 1 & v 2 x 1 y 2 1 v 4 = y 1 0 ~v 3 1 0 – 19 – = v 4 == v 5 0 x 0 y 1 1 1 x 1 y 2 t y 0 1 x 2 0 0 x 0 y 1 1 x | y 1 x 1 y 2 v 5 = y 0 0 x 2 0 x 0 0 y 0 1 1 0 1

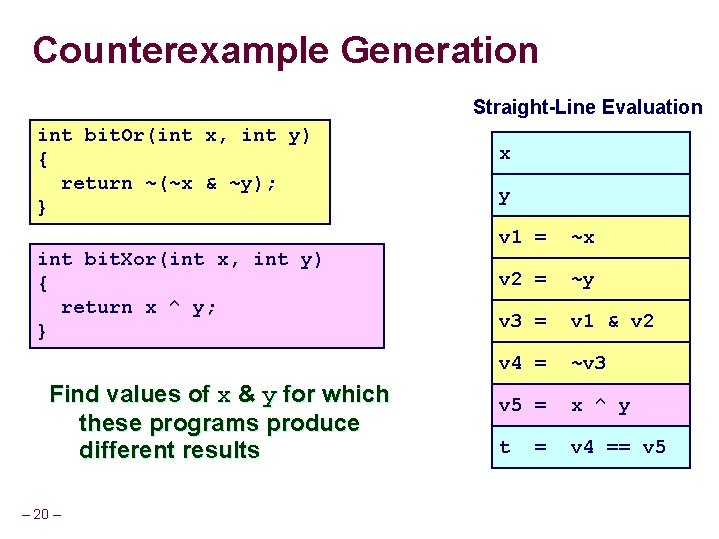
Counterexample Generation Straight-Line Evaluation int bit. Or(int x, int y) { return ~(~x & ~y); } int bit. Xor(int x, int y) { return x ^ y; } Find values of x & y for which these programs produce different results – 20 – x y v 1 = ~x v 2 = ~y v 3 = v 1 & v 2 v 4 = ~v 3 v 5 = x ^ y t v 4 == v 5 =

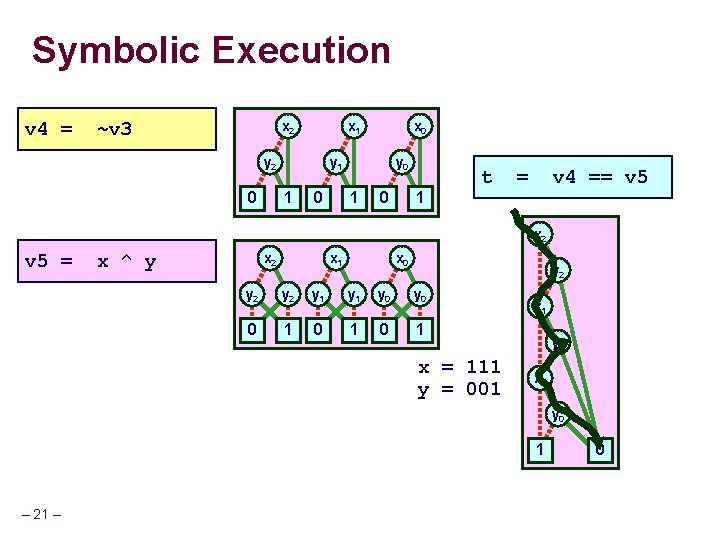
Symbolic Execution v 4 = ~v 3 x 2 x 1 y 2 0 x 0 y 1 1 0 y 0 1 0 t = v 4 == v 5 1 x 2 v 5 = x ^ y x 2 x 1 x 0 y 2 y 2 y 1 y 0 0 1 0 1 x = 111 y = 001 x 1 y 1 x 0 y 0 1 – 21 – 0

Performance: Good int add. XY(int x, int y) { return x+y; } – 22 – int add. YX(int x, int y) { return y+x; }

Performance: Bad int mul. XY(int x, int y) { return x*y; } – 23 – int mul. YX(int x, int y) { return y*x; }

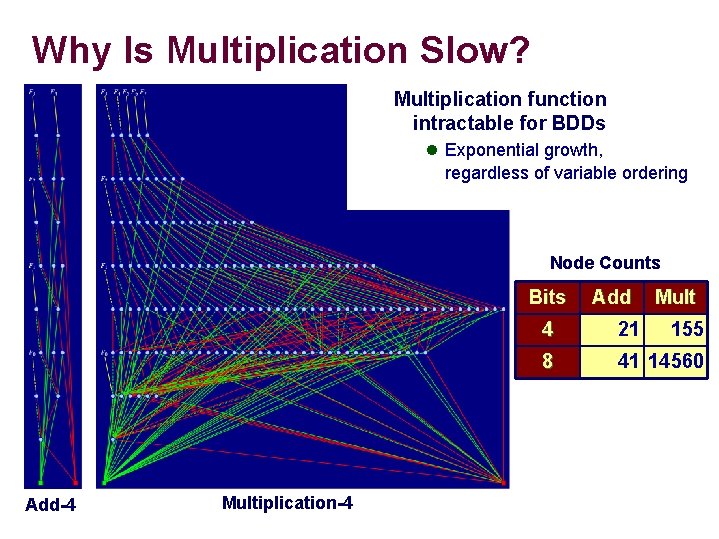
Why Is Multiplication Slow? Multiplication function intractable for BDDs l Exponential growth, regardless of variable ordering Node Counts Bits Add-4 – 24 – Multiplication-4 Add Mult 4 21 155 8 41 14560

What if Multiplication were Easy? int factor. K(int x, int y) { int K = XXXX. . . X; int range. OK = 1 < x && x <= y; int factor. OK = x*y == K; return range. OK && factor. OK; } – 25 – int zero(int x, int y) { return 0; } n Determine case where factor. K(x, y) != zero(x, y) n Would enable us to factor numbers

Evaluation of Bit-Level Checking Application n BDD version used on student programming examples n Similar capabilities provided by CBMC l Clarke, Kroening, Lerda, TACAS ’ 04 l Uses SAT solver Strengths n n Provides 100% guarantee of correctness Performance very good for simple arithmetic functions Weaknesses n n – 26 – Important integer functions have exponential blowup Not practical for programs that build and operate on large data structures

Model Checking Software Program is Hard to Model as Finite-State Machine n Large number of large data words means lots of bits l Although “finite”, bound is very large n Recursion requires stack l Conceptually unbounded Creating Abstraction n n – 27 – Focus on control structure of program Minimal modeling of data representations & operations

Microsoft SLAM Project http: //research. microsoft. com/slam/ Application n n – 28 – Windows device drivers Check adherence to Windows driver guidelines

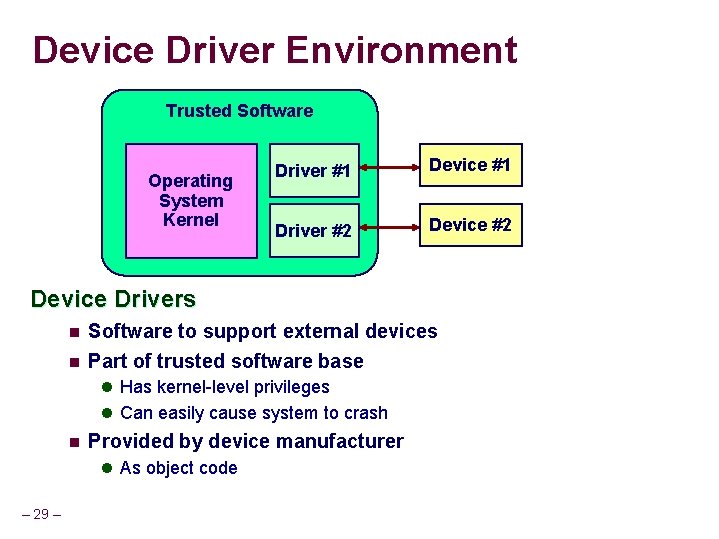
Device Driver Environment Trusted Software Operating System Kernel Driver #1 Device #1 Driver #2 Device Drivers n Software to support external devices n Part of trusted software base l Has kernel-level privileges l Can easily cause system to crash n Provided by device manufacturer l As object code – 29 –

SLAM Operation Abstraction / Refinement n Extract Boolean program from C code l Like C program, except only Boolean data types n n – 30 – Model check to find typical driver bugs Refine model if necessary

Code Verification Example n Adapted by Tom Ball from PCI device driver code do { lock(v); old = new; if (test()) { unlock(v); new++; } } while (new != old); unlock(v); – 31 – Properties to Check n n n Cannot unlock v unless locked Cannot lock v unless unlocked Must exit code with v unlocked

Model as Boolean Programming Model n Retain original control flow n Abstract data to be just Boolean values Initial abstraction n No data. Branches occur arbitrarily do { lock(); if (*) { unlock(); Apparent bug: May call lock twice } } while (*); unlock(); – 32 – Apparent bug: May call unlock twice

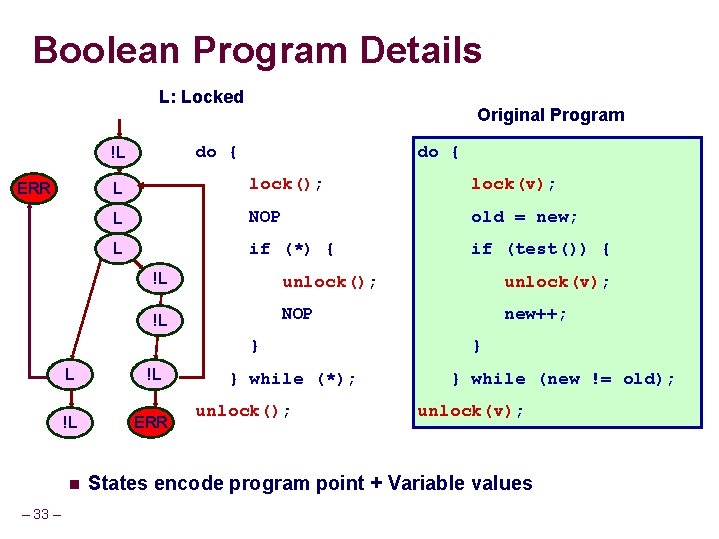
Boolean Program Details L: Locked do { !L ERR Original Program do { L lock(); lock(v); L NOP old = new; L if (*) { if (test()) { !L unlock(); unlock(v); !L NOP new++; } L !L !L ERR n – 33 – } while (*); unlock(); } } while (new != old); unlock(v); States encode program point + Variable values

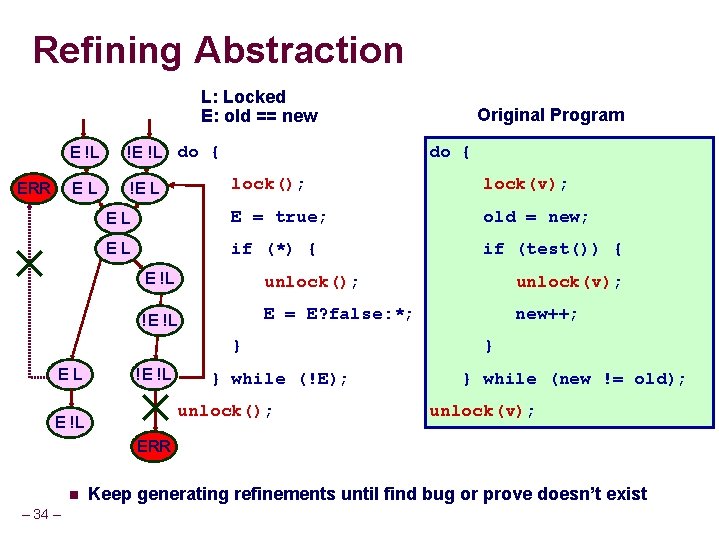
Refining Abstraction L: Locked E: old == new ERR E !L !E !L do { EL !E L do { lock(); lock(v); EL E = true; old = new; EL if (*) { if (test()) { E !L unlock(); unlock(v); !E !L E = E? false: *; new++; } EL Original Program !E !L } while (!E); unlock(); E !L } } while (new != old); unlock(v); ERR n – 34 – Keep generating refinements until find bug or prove doesn’t exist

Windows Success Story “Things like even software verification, this has been the Holy Grail of computer science for many decades but now in some very key areas, for example, driver verification we're building tools that can do actual proof about the software and how it works in order to guarantee the reliability” -- Bill Gates, Win. Hec Conference, 2002 Available in Windows Driver Development Kit n – 35 – Project moved from Microsoft Research into Windows Development Group

Why the Recent Successes in Software Verification? Need for Improved Software Quality n Worldwide network of hackers creates hostile testing environment Improved Technology n Program analysis + hardware verification tools Loss of Ambition n n – 36 – Bug finding rather than complete verification Vs. earlier attitude: must do complete verification of entire program

Some Research Challenges Understanding Memory References n In C, hard to determine whether two pointers refer to same object l Pointer aliasing n Real programs construct and manipulate complex data structures l Current verification techniques do best with control-intensive applications Working with Large Code Base n Runtime libraries l Even simple programs build upon extensive library code » Especially Java – 37 –

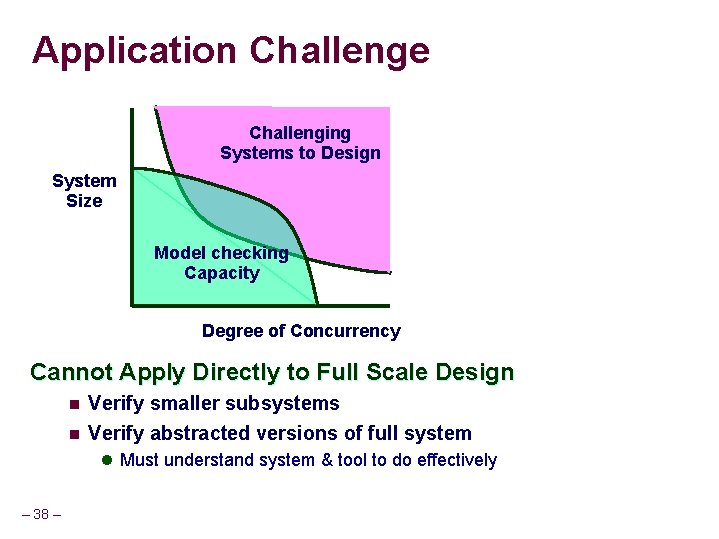
Application Challenge Challenging Systems to Design System Size Model checking Capacity Degree of Concurrency Cannot Apply Directly to Full Scale Design n Verify smaller subsystems n Verify abstracted versions of full system l Must understand system & tool to do effectively – 38 –