Automata theory An openended computer science discipline that

Automata theory • An open-ended computer science discipline that concerns an abstract device called an "automaton, " which performs a specific computational or recognition function.

Automata theory • Automaton - is derived from the Greek word automatos which means “acting of one’s own will” is more often used to describe non-electronic moving machines, especially those that have been made to resemble human or animal actions. - is a mathematical model for a finite state machine (FSM).

Terminologies • Lexical Analysis - is the process of converting a sequence of characters into a sequence of tokens. Programs performing lexical analysis are called lexical analyzers or lexers. A lexer consists of a scanner and a tokenizer. • Token – is a categorized block of text. The block of text corresponding to the token is known as a lexeme.

Terminologies • Set – A group or collection of objects element of a set is anything that belongs to the set. • Symbol - An arbitrary datum which has some meaning to or effect on the machine. Symbols are sometimes just called "letters". • Strings – A finite sequence of symbols chosen from some alphabet. – A finite string formed by the concatenation of a number of symbols. • The Empty Strings – The string with zero occurrences of symbols, denoted by ^.

Terminologies • Length of a String – the number of positions for symbols in the string. • Alphabet - A finite set of symbols. Frequently denoted by Σ, which is the set of letters in an alphabet. • Formal Language – A set of strings all of which are chosen from some *, where is a particular alphabet.

2 Ways of Describing the elements of a Set • Roster Method – Enumerate the elements. • Rule Method – Describe the elements using their common characteristics.

Notations • • • IR – set of real nos. Z – set of integers Z/o – non-pro integers Q – Set of rational nos. IN – Set of natural or counting nos.

Regular Expression • Language defining expression • Ex: 1. ) Let S = { 0, 1} • S* = strings from S • S* = {^, 0, 1, 00, 01, 10, 11, 010, 101, 000, 111, 001, 110, 1 00, 0000, 1111, 0101, 1010, …. . } 2. ) 3. ) 4. ) 5. ) S S = = {01, 1} {1, 01, 10} {00, 011, 010} {01, 10}

Hint to describe a language • Length of the string ( even / odd ) • Start / end • Sequence

Operations on RE • a + b = a or b (union) • a. b = a and b (concatenation) • a* = Loop (Kleene closure)

Given the RE, describe the language • • • 0+1 0 + 01 + 10 (0+1)* 1 (0+1) [ (0+1)1 ]* (0+1) [ (0+1) ]* (0+1) [ 1 (0+1) ]*

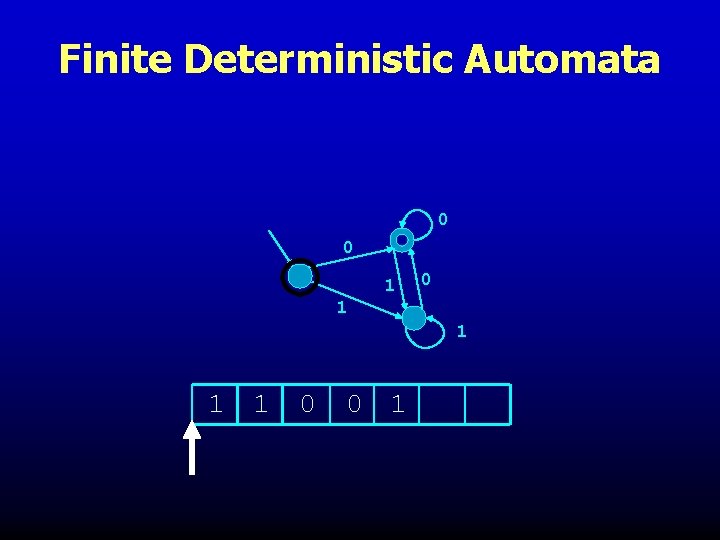
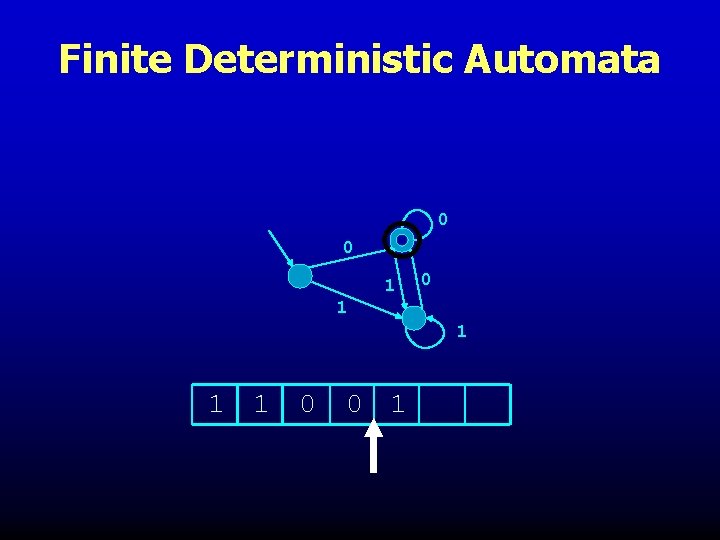
Finite Deterministic Automata More computer-like example: sourceless arrow denotes start input on tape read left to right double circle denotes accept 0 0 1 1 1 1 0 0 1

Finite Deterministic Automata 0 0 1 1 1 1 0 0 1

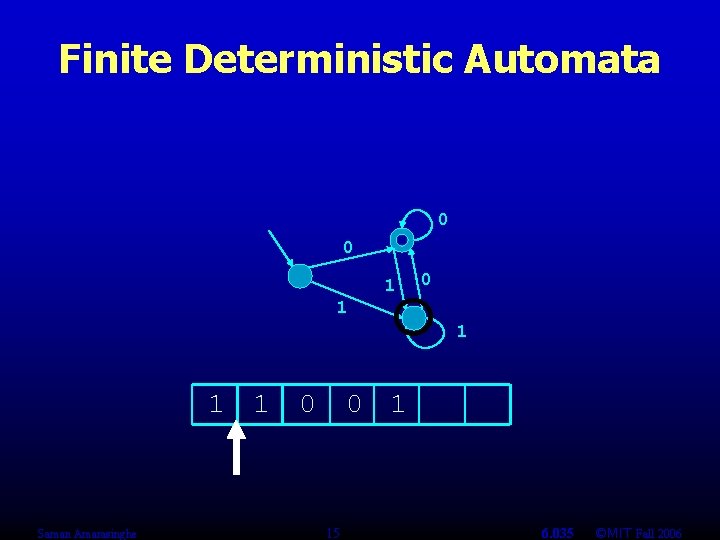
Finite Deterministic Automata 0 0 1 1 1 Saman Amarasinghe 1 0 0 1 15 6. 035 ©MIT Fall 2006

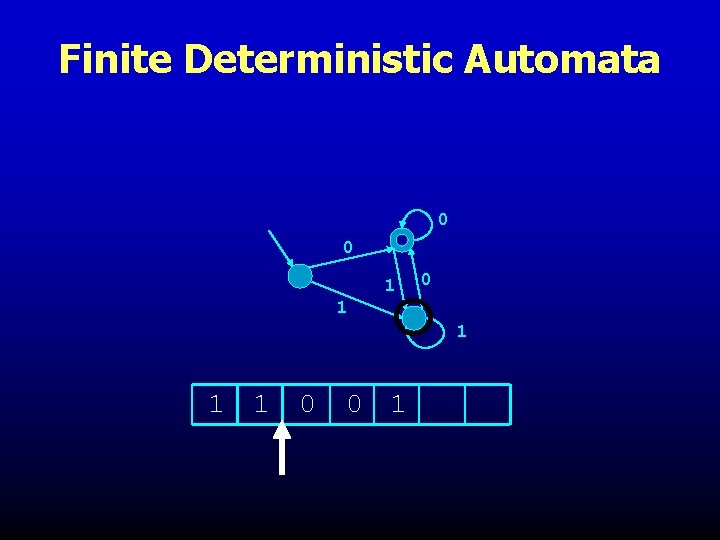
Finite Deterministic Automata 0 0 1 1 1 1 0 0 1

Finite Deterministic Automata 0 0 1 1 1 1 0 0 1

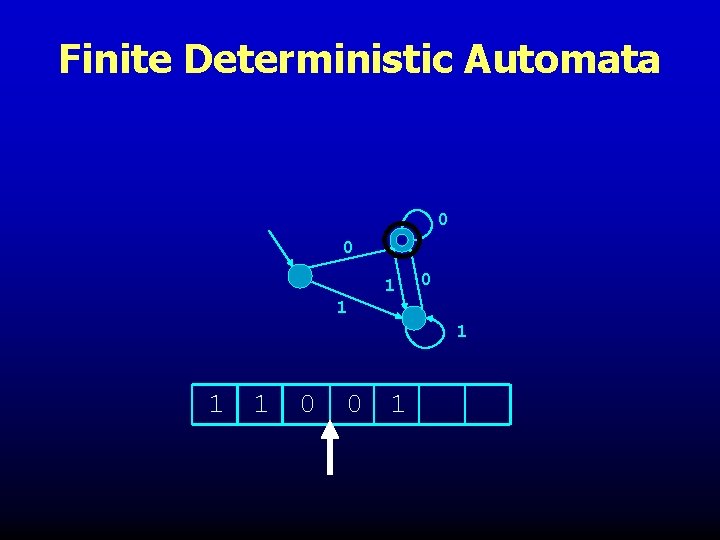
Finite Deterministic Automata 0 0 1 1 1 1 0 0 1

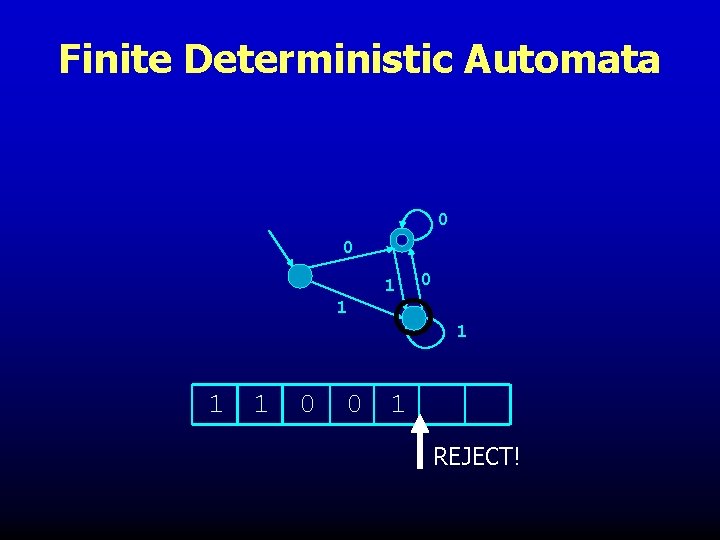
Finite Deterministic Automata 0 0 1 1 1 1 0 0 1 REJECT!

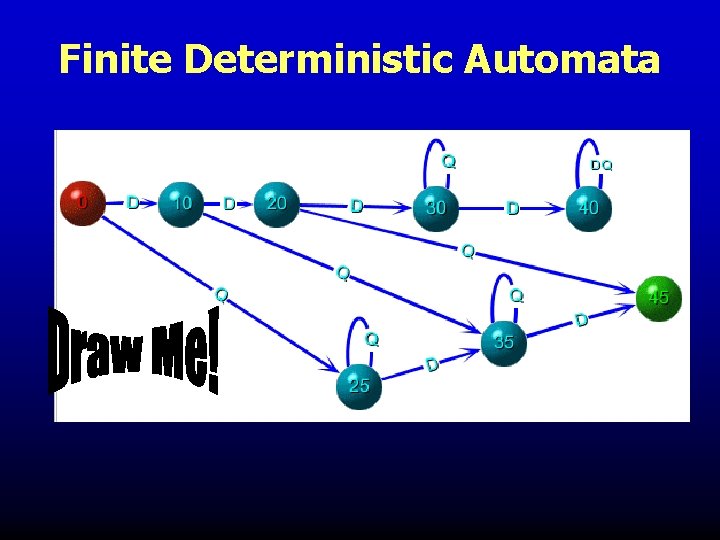
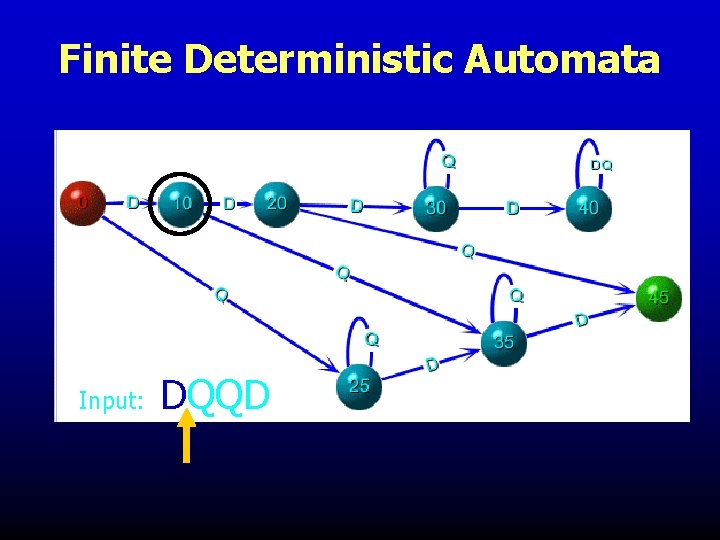
Finite Deterministic Automata

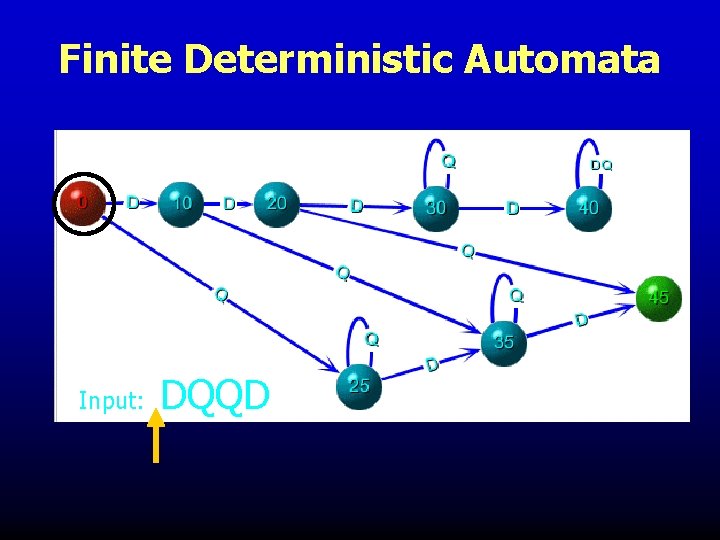
Finite Deterministic Automata Input: DQQD

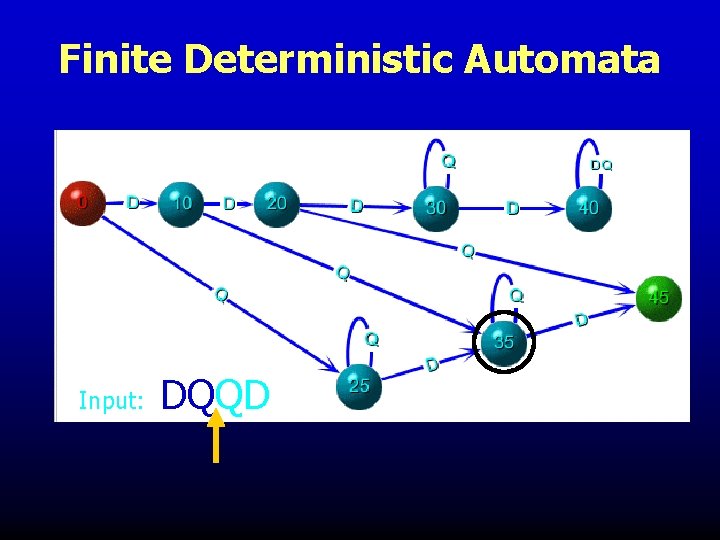
Finite Deterministic Automata Input: DQQD

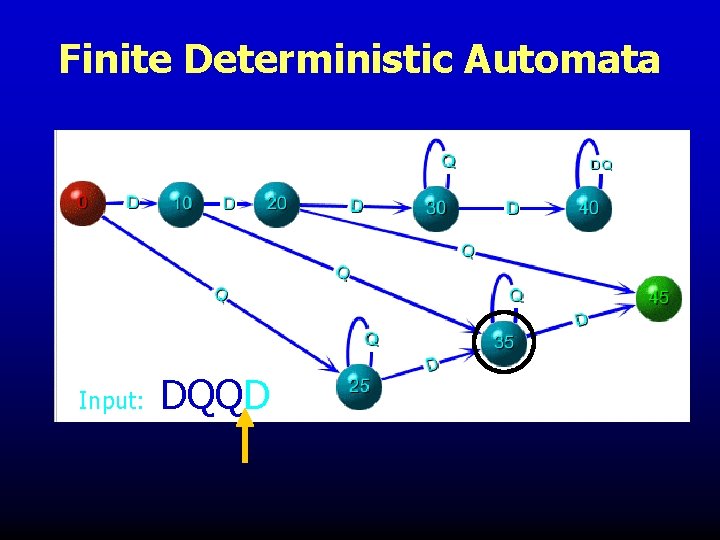
Finite Deterministic Automata Input: DQQD

Finite Deterministic Automata Input: DQQD

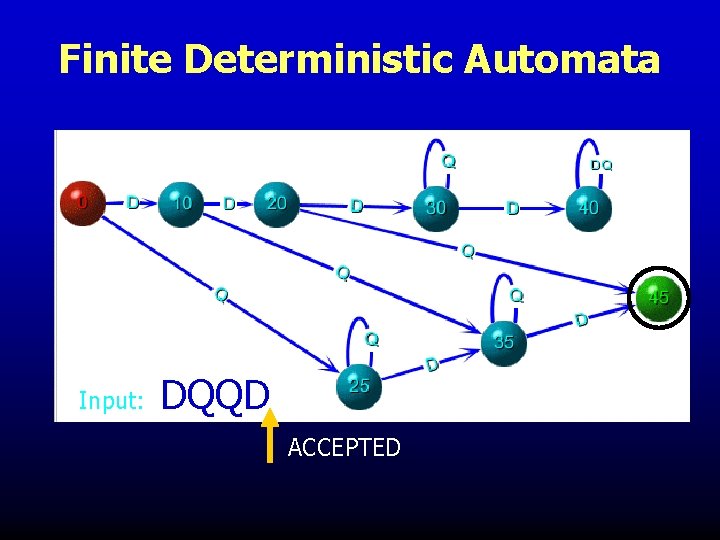
Finite Deterministic Automata Input: DQQD ACCEPTED