Automata and Languages What do these have in

Automata and Languages What do these have in common? Copyright © 2011 -2016 Curt Hill

Regular Expressions • The Finite State Machines that we have seen and regular expressions have equivalent power to express or recognize a language • What sort of languages can they accept? Or not accept? • How complicated may they be? • We now detour through formal languages Copyright © 2011 -2016 Curt Hill

Noam Chomsky • Professor emeritus of linguistics at MIT • Developed a theory of generative grammars • This includes a language hierarchy – AKA Chomsky-Schützenberger Hierarchy – Includes recursively enumerable, context sensitive, context free and regular Copyright © 2011 -2016 Curt Hill

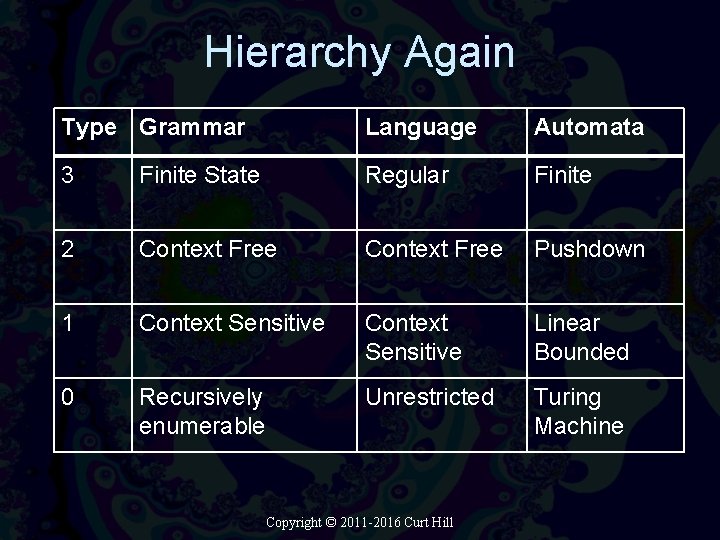
Language Hierarchies Type 3 Regular Type 2 Context Free Type 1 Context Sensitive Type 0 Unrestricted or Recursively enumerable Copyright © 2011 -2016 Curt Hill

Languages and Automata • Each of these languages corresponds to machine that can accept it • The weakest is a regular language, which can be accepted by a regular expression • Later machines correspond to stronger languages • Lets consider languages for a minute Copyright © 2011 -2016 Curt Hill

Formal Grammars • A grammar should be able to enumerate any legal sentence • Each grammar consists of four things • V – a finite set of non-terminals (aka variables) • T – a finite set of terminal symbols – Words made up from an alphabet • S – the start symbol – Must be an element of V • P – a set of productions Copyright © 2011 -2016 Curt Hill

C as an Example • V – set of non-terminals – Statement – Declaration – For-statement • T – set of terminals – Reserved words – Punctuation – Identifiers Copyright © 2011 -2016 Curt Hill

C example again • S – Start symbol – Independently compilable part – Program – Function – Constant • P – set of productions – Rewrite rules – Start at the start symbol – End at terminals – Before we consider productions we must consider notation Copyright © 2011 -2016 Curt Hill

John Backus • Principle designer of FORTRAN • Substantial contributions to ALGOL 60 • Designed Backus Normal Form • Eventually became a functional languages proponent • Turing award winner Copyright © 2003 -2014 by Curt Hill

BNF • John Backus defined FORTRAN with a notation similar to Context Free languages independent of Chomsky in 1959 • Peter Naur extended it slightly in describing ALGOL 60 • Became known as BNF for Backus Normal Form or Backus Naur Form • A meta-language is any language that describes another language Copyright © 2003 -2014 by Curt Hill

Simplest notation • Form of productions: LHS : : = RHS • Where: – LHS is a non-terminal (context free grammars) – RHS is any sequence of terminals and non-terminals, including empty – A common alternative to : : = is • There can be many productions with exactly the same LHS, these are alternatives • If the RHS contains the LHS, the rule is recursive. Copyright © 2003 -2014 by Curt Hill

Notation • There is usually a simple way to distinguish terminals and non-terminals • Rosen and others enclose nonterminals in angle brackets – <if> : : = if ( <condition> ) <statement> else <statement> Copyright © 2003 -2014 by Curt Hill

Simple extensions • Some times there is an alternation symbol that allows us to only need one production with the same LHS, often the vertical bar – <sign> : : = + | - • Some times things enclosed in [ and ] are optional, they may be present zero or one times • Some times things enclosed in { and } may be present 1 or more times – Thus [{x}] allows zero or more x items Copyright © 2003 -2014 by Curt Hill

More • The extensions are often called EBNF • Syntax graphs are equivalent to EBNF • These tend to be more easy to read Copyright © 2003 -2014 by Curt Hill

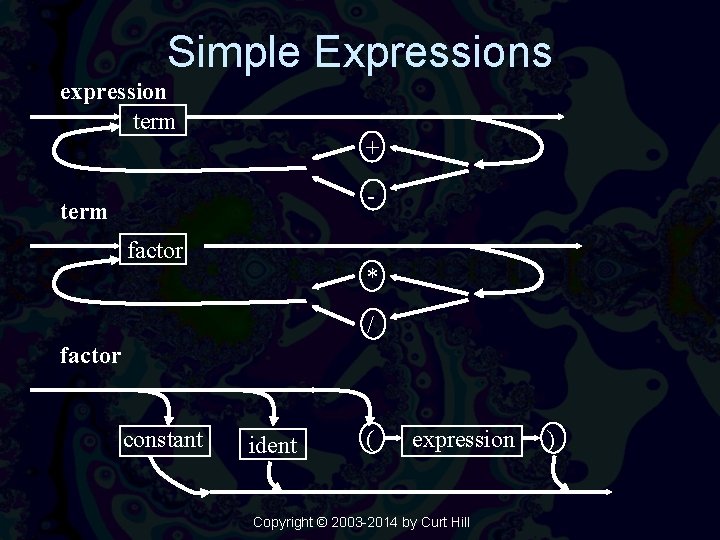
Syntax Graphs • A circle represents a terminal – Reserved word or operator – No further definition • A rectangle represents a non-terminal – For statement or expression – Must be defined else where • An arrow represents the path between one item and another – The arrows may branch indicating alternatives • Recursion is also allowed Copyright © 2003 -2014 by Curt Hill

Simple Expressions expression term + - term factor * / factor constant ident ( expression Copyright © 2003 -2014 by Curt Hill )

Productions • Productions may be represented as BNF, EBNF or syntax graphs • A production is a rewrite rule • We take a construction and find one way to rewrite it • In parsing we go from the distinguished symbol to any real program using application of these rewrite rules Copyright © 2011 -2016 Curt Hill

C For Production • For-statement : : = for ( expression; expression) statement • This contains the terminals: – For ( ; ) • Non-terminals – Expression – Statement Copyright © 2011 -2016 Curt Hill

Productions Again • Each non-terminal should have one or more productions that define it – Every non-terminal must have one or more productions • Multiple productions usually signify alternation • Recursion is allowed Copyright © 2011 -2016 Curt Hill

Recursion • • Productions may be recursive Recall for-statement, here is Statement : : = expression ; Statement : : = for-statement ; Statement : : = if-statement ; Statement : : = while-statement ; Statement : : = compound-statement Etc. Copyright © 2011 -2016 Curt Hill

Hierarchy Again Type Grammar Language Automata 3 Finite State Regular Finite 2 Context Free Pushdown 1 Context Sensitive Linear Bounded 0 Recursively enumerable Unrestricted Turing Machine Copyright © 2011 -2016 Curt Hill

How are these related? • Each of these grammars are related by how productions may be constructed • Regular are most restrictive • Unrestricted is the least restrictive • Lets compare – Upper case represent non-terminals – Lower case represent terminals Copyright © 2011 -2016 Curt Hill

Regular Grammars(3) • A : : = b | A : : = b. C | A : : = Cd • The production must have only one nonterminal on the left • The right-hand side must be: – A terminal followed by a non-terminal – A non-terminal followed by a terminal • May not have a terminal non-terminal on right – Terminal may lead or follow but not both Copyright © 2011 -2016 Curt Hill

Aside on Scanners • The first phase of a compiler is the lexical analyzer – AKA the scanner • It does the following: – Converts the source to a series of tokens – Removes comments and white space • The token stream is then used by the parser Copyright © 2011 -2016 Curt Hill

Scanners again • A token could be: – Any constant, usually typed – Any reserved word – Any punctuation mark – Any identifier • Parser inputs the stream of tokens • The scanner will often be just a finite state machine Copyright © 2011 -2016 Curt Hill

Context Free(2) • A : : = a. Ny • Single non-terminal on left • Any number or arrangement of nonterminals and terminals on the right • Most programming languages are largely context free – The optional else in C is not • These languages may be recognized by a pushdown machine Copyright © 2011 -2016 Curt Hill

Context Sensitive(1) • x A y : : = x a. Ny y • Left hand side may have nonterminal surrounded by optional terminals • If terminals are present on left they must also be on right • Any number or arrangement of nonterminals and terminals on the right in between terminals • Recognized by linear bounded Turing machine Copyright © 2011 -2016 Curt Hill

Unrestricted(0) • Anything on left and right • Terminals and non-terminals may be replaced by combinations of terminals and non-terminals in any combination • May be recognized by Turing machine Copyright © 2011 -2016 Curt Hill

Finally • It may seem strange that langauges and automata are related but they are • We find that most programming languages are context free – Sometimes with small exceptions • There a number of table driven parsers for context free languages Copyright © 2011 -2016 Curt Hill