Autmata finito Determinista Definicin Un AFD es una

Autómata finito Determinista

Definición �Un ◦ ◦ ◦ AFD es una quíntupla A =(Q, , , q 0, F) Q es un conjunto finito de estados es un alfabeto finito (símbolos de entrada) es una función de transición (q, a) p q 0 Q es el símbolo de inicio F Q es el conjunto de estados finales

Autómata finito � Transición s 1 a s 2 (s 1, a) s 2 � Se lee ◦ En el estado s 1 teniendo entrada ¨a¨ moverse al estado s 2

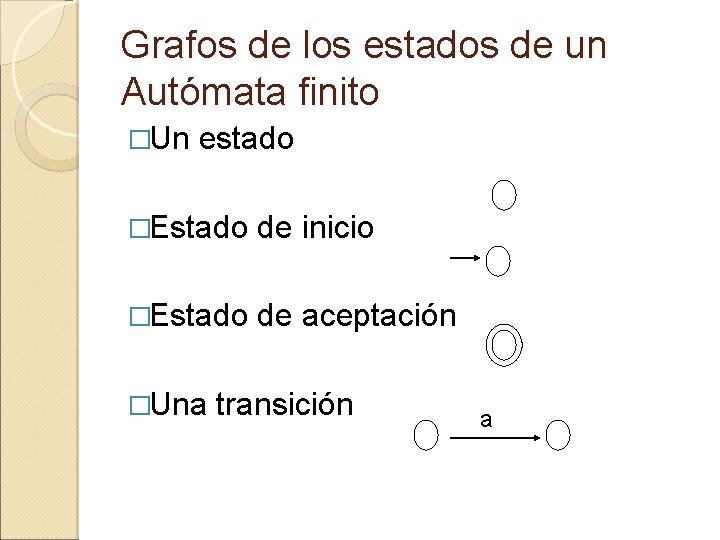
Grafos de los estados de un Autómata finito �Un estado �Estado de inicio �Estado de aceptación �Una transición a

Ejemplo 1 � Si se tiene el alfabeto ∑={0, 1} dibuje un autómata finito que acepte la cadena ¨ 1¨ q 1 r A={{q, r}, {0, 1}, (q, 1)=r, q, {r}} Un autómata finito acepta una cadena w si podemos seguir las etiquetas de los arcos con los caracteres de la cadena w desde el estado de inicio hasta un estado de aceptación

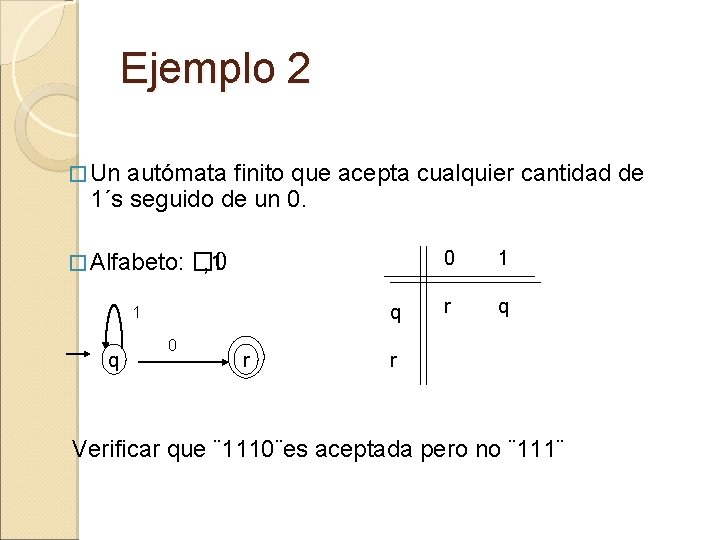
Ejemplo 2 � Un autómata finito que acepta cualquier cantidad de 1´s seguido de un 0. � Alfabeto: � 0 , 1 q 0 r 0 1 r q r Verificar que ¨ 1110¨es aceptada pero no ¨ 111¨

Implementación �Un AFD se puede implementar mediante una tabla de 2 dimensiones T ◦ Una dimensión para los estados ◦ Otra dimensión para los símbolos de entrada ◦ Para cada transición (s 1, a) s 2 definir T[i, a] = k �Ejecución del AFD ◦ Para cada estado si y entrada a, leer T[i, a]=k y saltar al estado k. ◦ Muy eficiente.

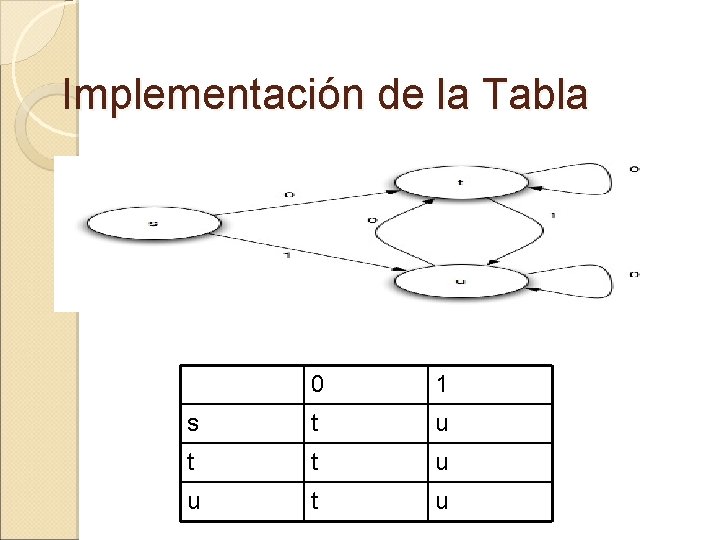
Implementación de la Tabla 0 1 s t u t t u u t u

Ejemplo 3 Un autómata A que ◦ {x 01 y: x, y {0, 1}*} El acepta autómata como un diagrama de transición

Ejemplo El autómata anterior, A=({q 0, q 1, q 2}, {0, 1}, , q 0, {q 1}) tiene tabla de transición:

Aceptación de una cadena por un Autómata Finito (AF) �Un AF acepta una cadena w=a 1 a 2…an si existe un camino en el diagrama de transición tal que: ◦ Comienza en el estado inicial. ◦ Finaliza en un estado de aceptación. ◦ Tiene una secuencia de etiquetas a 1 a 2…an

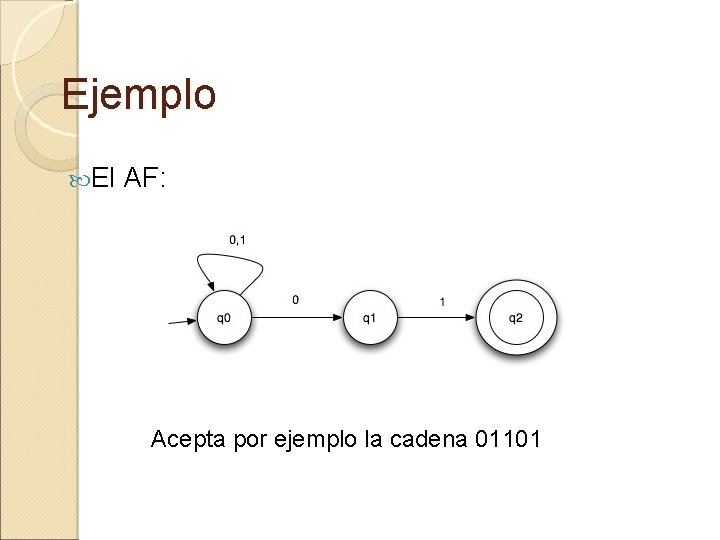
Ejemplo El AF: Acepta por ejemplo la cadena 01101

Extensión de la función de transición se puede extender a que opera en estados y cadenas (a diferencia de que opera en estados y símbolos). �La ◦ Caso base: (q, )=q ◦ Inducción: (q, xa)= ( (q, x), a)

Ejemplo �Empleando al autómata del ejemplo anterior, con la cadena 01101 genera el siguiente resultado: ◦ Realizarlo en clase.

Lenguaje aceptado por un AF �Formalmente el lenguaje aceptado por un AF llamado A es: L(A)= w (q 0, w) F Los lenguajes aceptados por AFs se conocen como regulares.

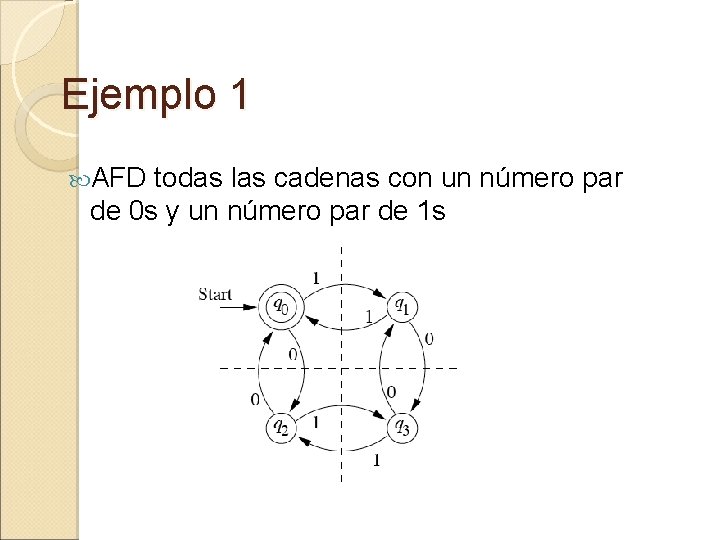
Ejemplo 1 AFD todas las cadenas con un número par de 0 s y un número par de 1 s

Ejemplo 1 (Cont. ) La tabla de transición del autómata es:

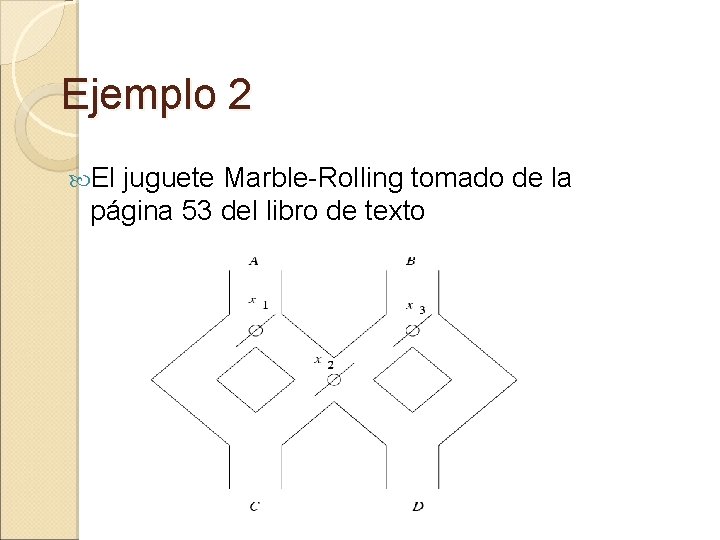
Ejemplo 2 El juguete Marble-Rolling tomado de la página 53 del libro de texto

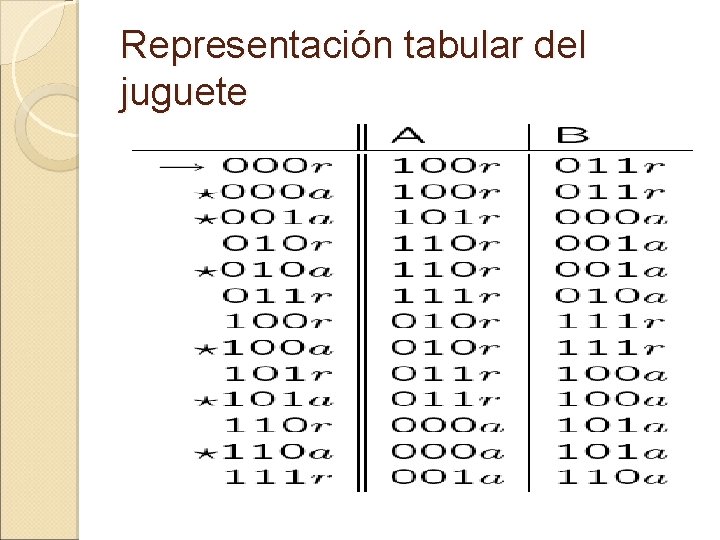
Ejemplo 2 (Cont. ) �Un estado se representa como una secuencia de 3 bits seguidos por r ó a (lo que significa que la entrada anterior fue rechazada o aceptada) �Por ejemplo, 010 a significa, izquierda, derecha, izquierda aceptada.

Representación tabular del juguete