Aula Terica 6 Estabilidade Critrio de Routh Critrio

Aula Teórica 6: Estabilidade – Critério de Routh. Critério de estabilidade de Routh Erro de estado estacionário (Desempenho em Regime Permanente)

Critério de Estabilidade de Routh É um método fácil que permite saber se o sistema é ou não estável Estabilidade absoluta Também permite limitar a fila em que devem estar alguns parâmetros para que o sistema seja estável

Considere a seguinte função de transferência de malha fechada: Primeiro passo Escreva a equação polinomial onde elimina-se qualquer raiz zero Nota: Se algum dos coeficientes é zero ou negativo em presenca de pelo menos um coeficiente positivo há uma raiz ou raízes imaginárias ou que tem partes reais positivas. O sistema não é estável e se interrompe o método aqui

Segundo passo Montar a seguinte tabela: Se todos os coeficientes forem positivos

Terceiro passo Aplicar o critério do Routh que diz “O número de raízes da equação característica com partes reais positivas é igual ao número de mudanças de sinal dos coeficientes da 1 a coluna da tabela”. EXEMPLO: Duas mudanças Duas raízes com parte real positiva Sistema Instável

Casos Especiais a) Primeiro termo de uma linha é nulo: -Substituir o termo nulo por um número positivo muito pequeno e continuar a completar a tabela ou - Multiplicar o polinômio por (s+1) e construir a tabela EXEMPLO: Duas mudanças Duas raízes com parte real positiva Sistema Instável

b) Todos os coeficientes em uma linha são nulos: - O resto da tabela pode ser continuado formando um polinômio auxiliar com os coeficientes da última linha e usando os coeficientes da derivada deste polinômio na linha seguinte. EXEMPLO: derivando Uma mudança Uma raíz com parte real positiva Sistema Instável

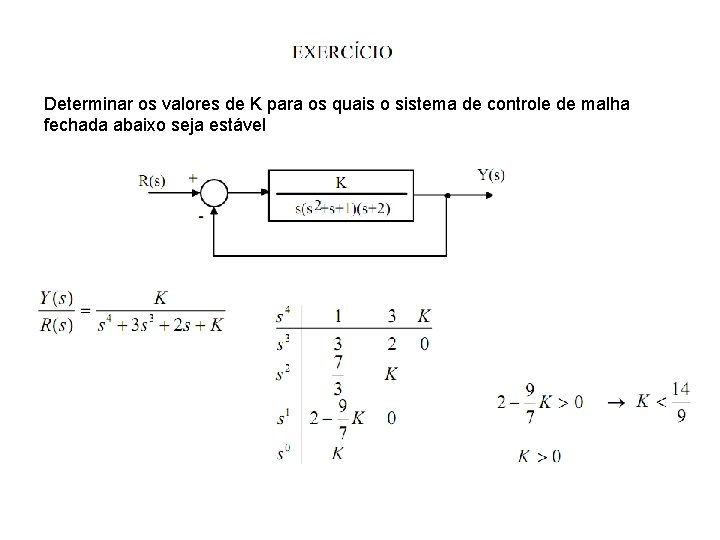
Determinar os valores de K para os quais o sistema de controle de malha fechada abaixo seja estável

Desempenho em Regime Permanente A análise do desempenho em regime permanente de um sistema consiste no estudo do comportamento da resposta do sistema quando o tempo tende a infinito. Este comportamento tem muita relação com uma classificação para os sistemas de controle que até agora vocês não conhecem

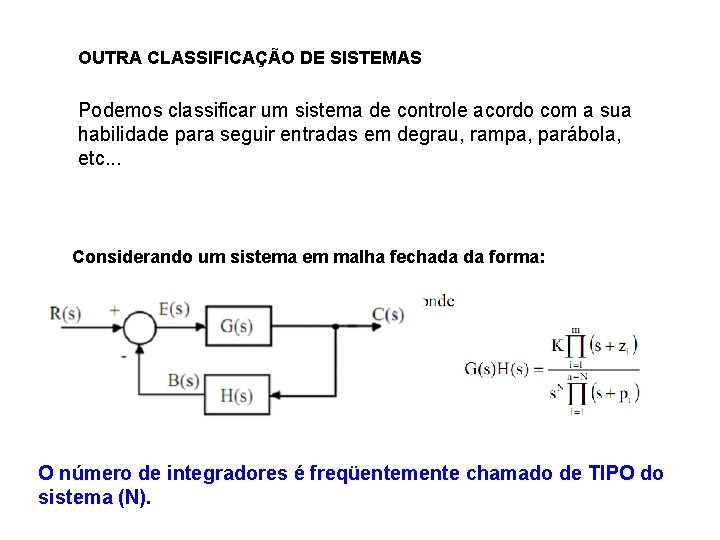
OUTRA CLASSIFICAÇÃO DE SISTEMAS Podemos classificar um sistema de controle acordo com a sua habilidade para seguir entradas em degrau, rampa, parábola, etc. . . Considerando um sistema em malha fechada da forma: O número de integradores é freqüentemente chamado de TIPO do sistema (N).

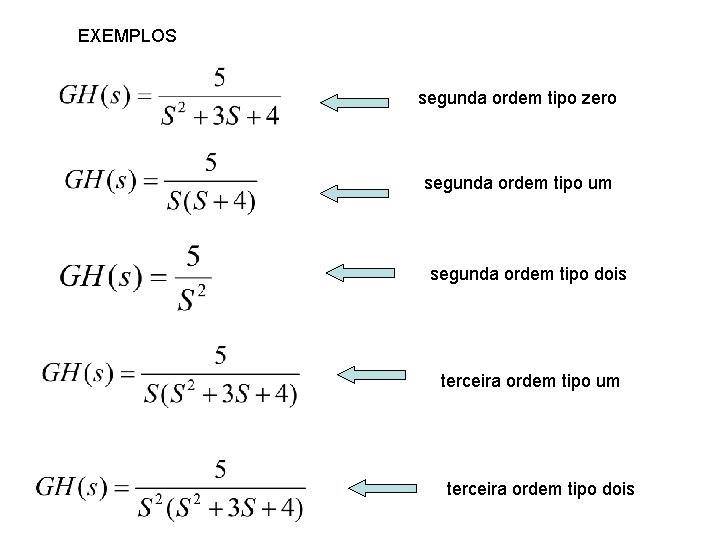
EXEMPLOS segunda ordem tipo zero segunda ordem tipo um segunda ordem tipo dois terceira ordem tipo um terceira ordem tipo dois

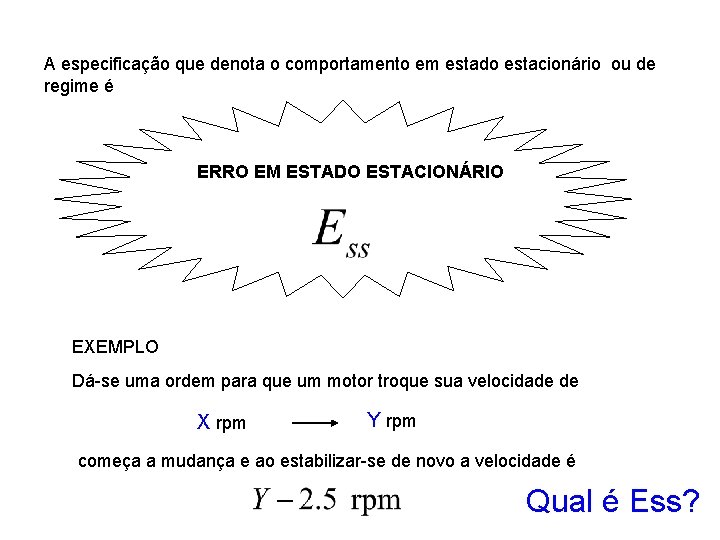
A especificação que denota o comportamento em estado estacionário ou de regime é ERRO EM ESTADO ESTACIONÁRIO EXEMPLO Dá-se uma ordem para que um motor troque sua velocidade de X rpm Y rpm começa a mudança e ao estabilizar-se de novo a velocidade é Qual é Ess?

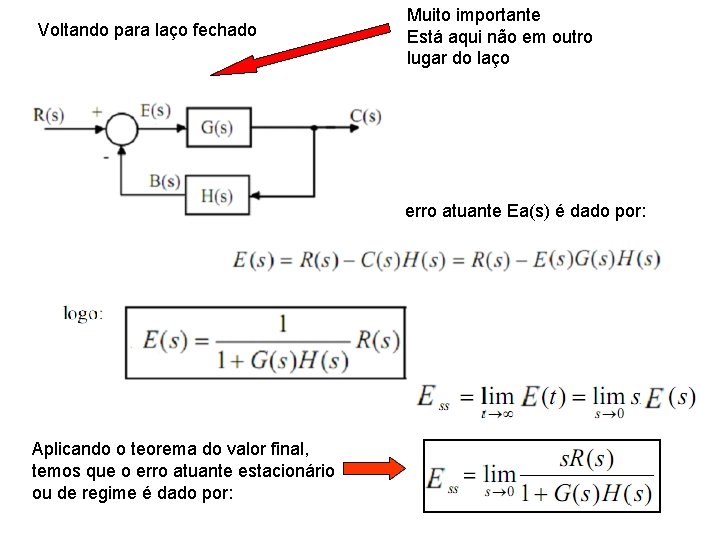
Voltando para laço fechado Muito importante Está aqui não em outro lugar do laço o erro atuante Ea(s) é dado por: Aplicando o teorema do valor final, temos que o erro atuante estacionário ou de regime é dado por:

OBSERVAÇÃO IMPORTANTE A entrada está na expressão do engano por isso este último dependerá entre outras coisas dela 1 ro O erro de regime para uma entrada degrau de magnitude A é:

2 do Entrada Rampa O erro de regime para uma entrada rampa de inclinação A é: Definindo a constante de erro de velocidade estático (Kv) como:

3 ro

Resumindo até aqui Que relação guarda isto com o tipo de sistema?

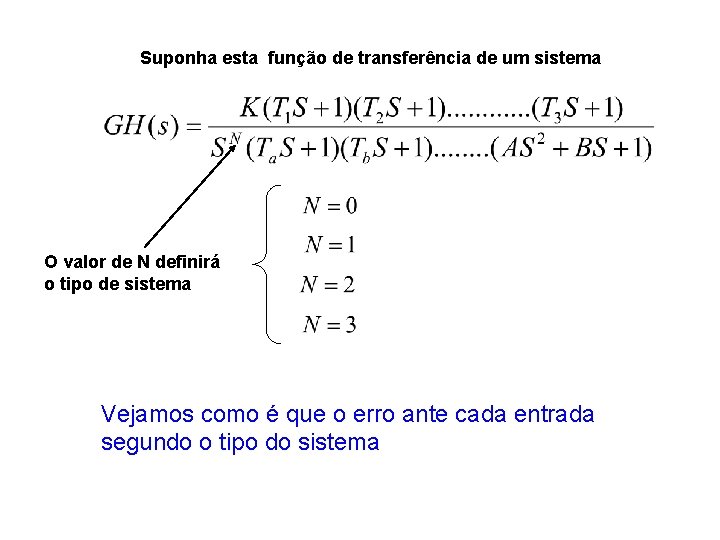
Suponha esta função de transferência de um sistema O valor de N definirá o tipo de sistema Vejamos como é que o erro ante cada entrada segundo o tipo do sistema

Tipo zero Um sistema tipo zero segue a uma entrada degrau com um erro e nunca seguirá a uma rampa ou uma parábola

Tipo um Um sistema tipo um segue com total exatidão a entrada degrau, pode seguir uma entrada rampa com um erro e nunca seguirá uma parábola

Tipo dois Um sistema tipo dois pode seguir com exatidão uma entrada degrau e uma entrada rampa mas a uma parábola a segue com um erro

Resumo