AULA 8 Fernando Luiz Pellegrini Pessoa TPQBq ESCOLA

AULA 8 Fernando Luiz Pellegrini Pessoa TPQBq ESCOLA DE QUÍMICA UNIVERSIDADE FEDERAL DO RIO DE JANEIRO

Equações de Estado • São expressões analíticas que relacionam as propriedades volumétricas de um fluido da seguinte forma:

Equações de Estado · Equação do gás ideal · Equação do virial · Equações cúbicas · Equações não-cúbicas

Equação do Gás Ideal À temperatura constante onde V é o volume molar

Equação do Gás Real onde Z é o fator de compressibilidade

Fator de compressibilidade do isobutano a 380 e 420 K

Observações • A pressões baixas, as moléculas estão muito afastadas umas das outras, e não há forças intermoleculares. O fluido se comporta como um gás ideal (Z=1). • À medida que a pressão aumenta, as moléculas vão se aproximando umas das outras e as forças de atração intermolecular tornam-se dominantes. Logo, o volume diminui mais do que deveria diminuir se não houvesse forças de atração intermolecular e Z<1. • A pressões muito altas, as moléculas ficam muito próximas umas das outras, de tal forma que as forças repulsivas tornam-se dominantes. Como consequência, o volume aumenta mais do que deveria aumentar se não houvesse forças de repulsão intermolecular e Z > 1. • Há um valor de Z=1, para altas pressões, mas que não corresponderá ao comportamento de gás ideal.

Equação do virial • É obtida a partir da expansão de Z como uma série de potências de (1/V), a certa temperatura T, e pressão P 0, da seguinte forma: • Essa equação pode ser escrita em termos de uma expansão em série de potências para a pressão, dada por: • Os 2 o e 3 o. coeficientes viriais dessas 2 equações se relacionam da seguinte forma:

Equação do virial • Na prática, a equação virial é utilizada truncada no 2 o termo. O segundo coeficiente virial pode ser obtido de 2 formas: – A partir de dados PVT experimentais; – A partir de correlações empíricas (predição), na ausência de dados PVT (Ex: correlações de Tsonopoulos, Hayden. O’Connell, etc. )

Cálculo de propriedade de mistura usando a eq. do virial • Nesse caso, é preciso levar em conta a composição da mistura. • Se a equação do virial for truncada após o segundo coeficiente virial, o coeficiente de fugacidade do componente i na mistura pode ser calculado por:

Equações de Estado Cúbicas • Premissa: o desvio da idealidade se deve às forças intermoleculares (repulsivas e atrativas), que exercem papel preponderante no comportamento PVT do fluido. • As forças repulsivas dão uma contribuição positiva à pressão (PR>0) e as forças atrativas dão uma contribuição negativa à pressão (PA<0).
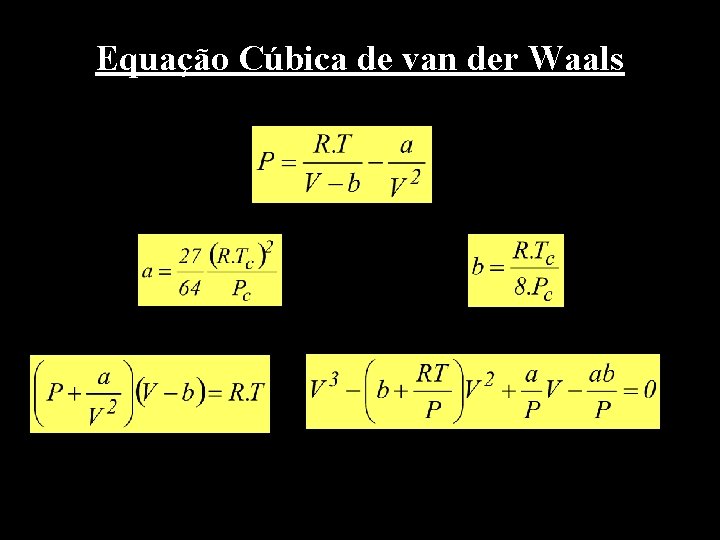
Equação Cúbica de van der Waals

Observação • As EEC devem descrever o comportamento dos fluidos no ponto crítico, satisfazendo as condições matemáticas nesse ponto, dadas pelas seguintes equações: onde P = Pc e V = Vc. • Os parâmetros a e b são determinados a partir dessas equações.
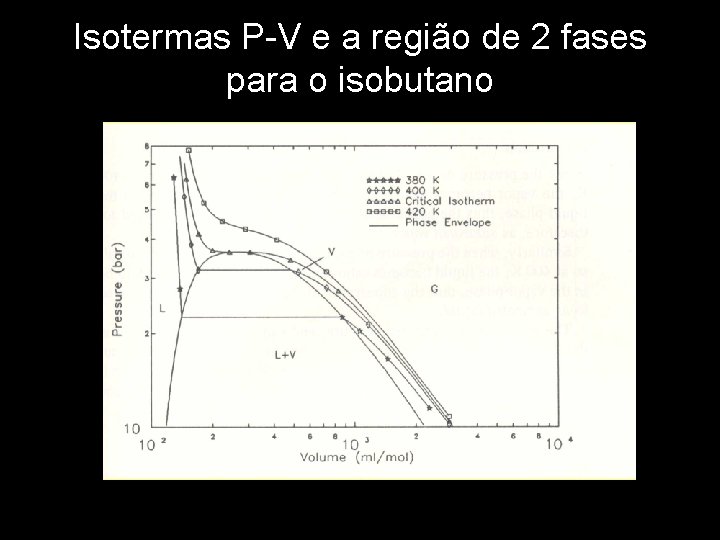
Isotermas P-V e a região de 2 fases para o isobutano

Comportamento PVT calculado pela equação de van der Waals
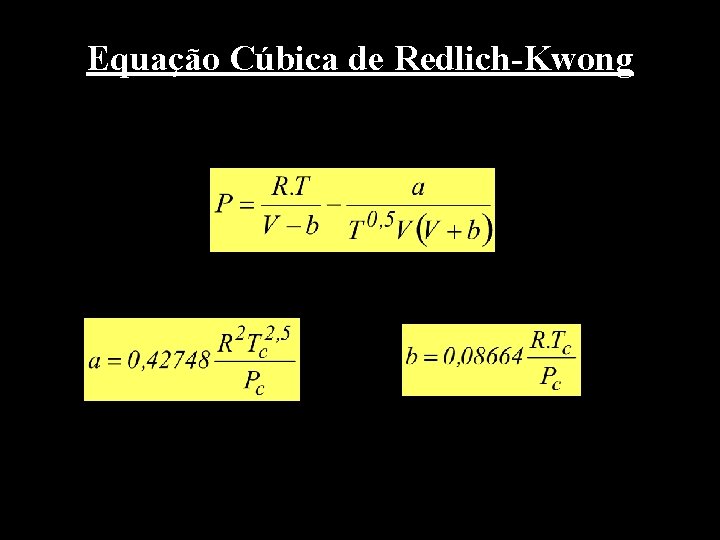
Equação Cúbica de Redlich-Kwong
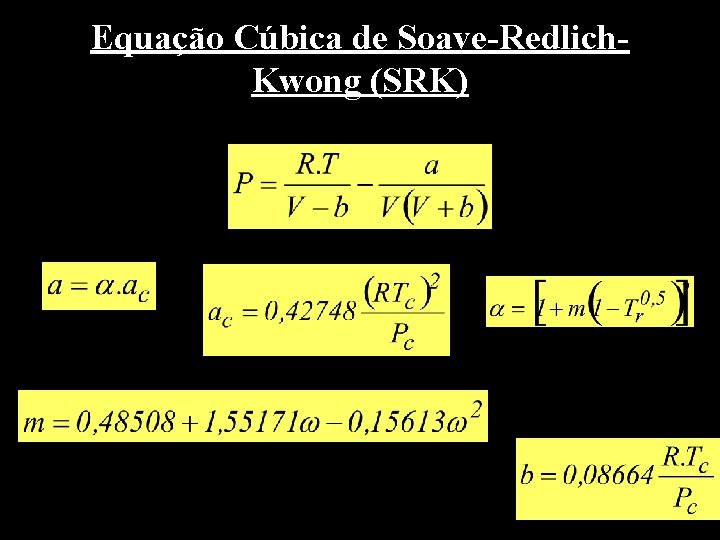
Equação Cúbica de Soave-Redlich. Kwong (SRK)

Equação Cúbica de Peng-Robinson

Forma generalizada das EECs (explícita em P)

Forma generalizada das EECs (explícita em Z)

Observações • A temperaturas supercríticas (T>Tc), todas as EEC, quando resolvidas para o volume, apresentam 1 raiz real e 2 raízes complexas. • A temperaturas subcríticas (T<Tc), as EEC podem ter até 3 raízes reais. Nesse caso, a maior raiz corresponde ao volume do vapor, a menor raiz é o volume da fase líquida e a raiz intermediária não tem significado físico. • As EECs cujo parâmetro a não seja função da temperatura (ex: vd. W e RK) não dão bons resultados para o cálculo da pressão de vapor.

Observações • As EECs cujo parâmetro a é função da temperatura (ex: SRK e PR) dão bons resultados para o cálculo da pressão de vapor de compostos apolares. • As EECs SRK e PR dão bons resultados também para o volume molar do vapor. • Para compostos apolares e Tr<1, os resultados do cálculo de volume do vapor são satisfatórios. Para Tr=1 e Pr>1, os resultados apresentam grandes erros, pois o volume nessa região é muito sensível à pressão.

Cálculo de propriedade de mistura usando EECs • Nesse caso, utilizam-se as seguintes regras de mistura:

Observações • Os valores do parâmetro de interação binária (kij) são obtidos a partir de dados experimentais de equilíbrio da mistura do componente i com o componente j. • Valores típicos de kij estão na faixa de 0 a 0, 2, para sistemas apolares ou fracamente polares, podendo ser bem maiores ou mesmo negativos, para sistemas polares. • Os valores de kij variam de EEC para EEC. Para sistemas com hidrocarbonetos de tamanhos próximos, pode-se utilizar kij=0.

Observações • O mesmo método preditivo utilizado para as substâncias puras pode ser estendido para as misturas. Porém, a qualidade dos resultados vai depender da disponibilidade dos parâmetros de interação binária. • Para o cálculo do comportamento volumétrico misturas gasosas de hidrocarbonetos até pressões moderadas, as EECs dão bons resultados mesmo para kij=0

Modelagem de Misturas Líquidas • Fugacidade de misturas líquidas – Abordagem • Modelos de GE – Modelos empíricos – Modelos de composição local

Fugacidade de Misturas Líquidas • O critério de equilíbrio entre 2 fases e , na mesma temperatura, é dado pela igualdade das fugacidades de cada componente i nessas fases: • Quando uma das fases em equilíbrio é uma mistura líquida, tem-se que pode ser calculada de 2 modos diferentes: – Abordagem

Abordagem • Analogamente ao cálculo de fugacidade de misturas gasosas, a abordagem utiliza a seguinte expressão para o cálculo da fugacidade do componente i numa mistura líquida: • Para o cálculo do coeficiente de fugacidade do componente i na mistura líquida, é preciso utilizar modelos que descrevem o comportamento volumétrico da mistura (equações de estado), já que

Abordagem • Na abordagem , a fugacidade do componente i na mistura líquida é calculada pela expressão: que depende do estado de referência ( ), para se calcular o desvio do comportamento de uma solução ideal • Quando a solução ideal segue a lei de Raoult: e a fugacidade do componente i na solução real é: • Quando a solução ideal segue a lei de Henry: e a fugacidade do componente i na solução real é:

Observação Em muitos sistemas a Lei de Raoult usa como estado de referência o líquido puro saturado, na mesma T e P da mistura. Nesse caso, a fugacidade do componente i na fase líquida é escrita como

Normalização de coeficientes de atividade • Lei de Raoult para soluto e solvente (convenção simétrica) • Lei de Raoult para solvente e lei de Henry para soluto (convenção assimétrica) – para o solvente: – para o soluto:

Relação entre os coeficientes de atividade simétrico e assimétrico • Se então

Observação Pela sua própria definição, a constante de Henry é dada por:

Fugacidade do Soluto dada pelas Leis de Henry e Raoult

Coeficiente de Atividade e Energia Livre de Gibbs em Excesso • A energia livre de Gibbs em excesso e o coeficiente de atividade estão relacionados da seguinte forma:

Modelos de GE Os modelos de GE devem ser capazes de descrever a nãoidealidade de uma mistura líquida. A T e P constantes, o processo de mistura é acompanhado de 3 efeitos: • O efeito energético, decorrente das diferenças de energia intermolecular entre as moléculas • O efeito volumétrico, que provoca a expansão ou contração do volume, devido às diferenças tanto de energia intermolecular quanto de tamanho e forma das moléculas • O efeito entrópico, resultante da perda de aleatoriedade na distribuição das moléculas na mistura, originada pelas diferenças de tamanho e forma das moléculas

Modelos de GE • Para entender a influência desses efeitos no processo de mistura, é conveniente escrever a energia livre de Gibbs em excesso da seguinte forma: • O efeito energético predomina nas misturas em que as diferenças de tamanho entre as moléculas não significativas. Assume-se que SE=0 e VE=0 , ou seja, • Quando há diferenças significativas de tamanho entre as moléculas, o efeito entrópico predomina:

Modelos de GE • Os modelos de GE desenvolvidos para misturas em que o efeito energético predomina dividem-se basicamente em 2 grupos: – Modelos empíricos – Modelos semi-empíricos ou de “composição local” • Para uma mistura binária, para a qual o estado padrão de cada componente da mistura é o líquido puro na mesma T e P da mistura, a energia livre de Gibbs em excesso deve obedecer às seguintes condições limites:

Modelos empíricos para GE A equação de Margules é um caso especial da expansão Redlich-Kister: Eq. de Margules

Modelos empíricos para GE Equação de Margules de 2 sufixos: aplica-se a misturas líquidas de moléculas de tamanho, forma e natureza química parecidas, a baixas e moderadas pressões.

Modelos empíricos para GE Equação de Margules de 3 sufixos:

Modelos empíricos para GE Equação de van Laar: aplica-se a misturas líquidas cujos componentes têm natureza química similar, mas os tamanhos das moléculas são diferentes

Modelos semi-empíricos ou de composição local para GE Conceito de composição local (Wilson, 1964) • Numa solução binária, a composição macroscópica não corresponde à composição microscópica, ou seja, as moléculas dos 2 componentes não se distribuem uniformemente na mistura líquida, ocorrendo duas situações: – A molécula do componente 1 cercada por outras moléculas (tanto de 1 como de 2) – A molécula do componente 2 cercada por outras moléculas (tanto de 1 como de 2);
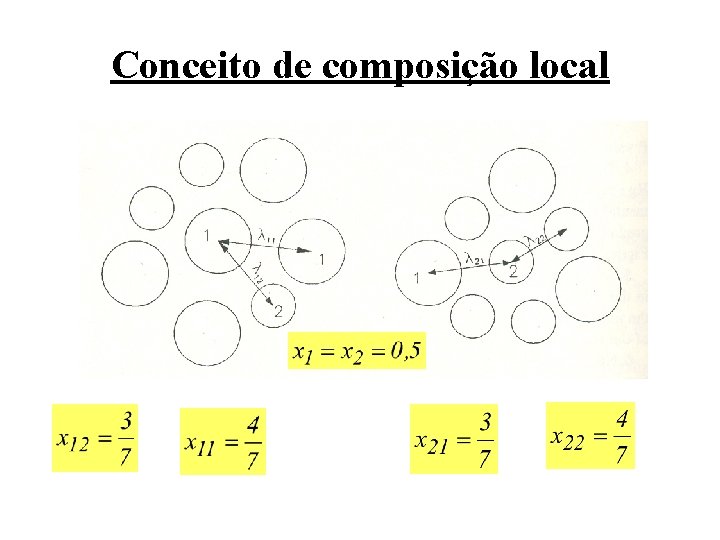
Conceito de composição local

Modelos de Composição Local para GE Equação de Wilson

Modelos de Composição Local para GE Equação NRTL Melhoria da equação de Wilson, introduzindo um terceiro parâmetro ( ), para considerar o fato das misturas líquidas serem não-randômicas (efeito entrópico). Os parâmetros ajustáveis são (=0, 3), e

Modelos de Composição Local para GE Coeficientes de Atividade da Equação NRTL

Modelos de Composição Local para GE Equação NRTL para um Sistema Multicomponente

Modelos de Composição Local para GE Equação UNIQUAC Melhoria das equações anteriores, levando em conta não apenas o conceito de composição local, mas também o efeito das diferenças de tamanho entre as moléculas, contabilizado através de parâmetros estruturais obtidos a partir de dados componentes puros. • A expressão de GE é dada como a soma de 2 contribuições: a combinatorial, que reflete as diferenças de tamanho e forma entre as moléculas da mistura, e a residual, que reflete as diferenças de energia de interação entre as moléculas da mistura.

Modelos de Composição Local para GE Equação UNIQUAC para uma mistura binária

Modelos de Composição Local para GE Coeficiente de Atividade da Equação UNIQUAC para uma mistura binária

Modelos de Composição Local para GE Equação UNIQUAC para um sistema multicomponente

Modelos de Composição Local para GE Modelo UNIFAC Foi desenvolvida a partir do modelo UNIQUAC, introduzindo o conceito de contribuição de grupos. Contribuição de Grupos Esse conceito baseia-se na idéia de que as propriedades de uma mistura podem ser calculadas, aproximadamente, considerando a soma das contribuições individuais dos grupos funcionais existentes nas moléculas presentes nessa mistura.

Modelos de Composição Local para GE Equação UNIFAC • A parte combinatorial deste modelo é igual à do UNIQUAC, só que nesse caso os parâmetros “r” e “q” de cada componente puro são calculados como a soma das respectivas contribuições de volume Rk e de área superficial Qk de cada grupo constituinte da molécula, ou seja,

Modelos de Composição Local para GE Equação UNIFAC • A parte residual do coeficiente de atividade é dada por
- Slides: 55













































































