AULA 5 TOPOGRAFIA AZIMUTES E RUMOS Prof Arildo

AULA 5 TOPOGRAFIA AZIMUTES E RUMOS Prof. Arildo 2013

AZIMUTE Segundo Mc. Cormac (2007), um termo comum utilizado para designar uma direção de uma linha é azimute. O azimute de uma linha é definido pelo ângulo em sentido horário do extremo norte ou sul do meridiano de referência para a linha em questão.

Para levantamentos planos comuns (utilizados em áreas relativamente pequenas onde se considera a Terra como plana), os azimutes são geralmente medidos à partir o lado norte do meridiano. O valor de um azimute pode variar de 0 a 360°.

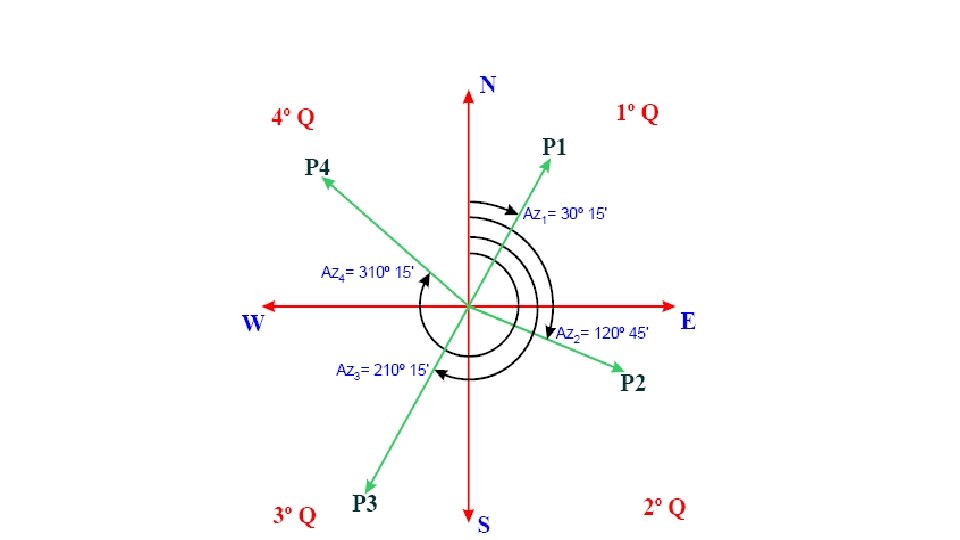
Em topografia e geodésia, os quadrantes do círculo trigonométrico da matemática são contados no sentido horário, da mesma forma, os azimutes também são contados no sentido horário a partir da direção norte que por sua vez coincide com o eixo das ordenadas ou Y de um sistema cartesiano.

Em levantamentos topográficos de terrenos são medidos ângulos e distâncias entre pontos que formam um alinhamento ou lados de uma poligonal os quais devem ter uma orientação segundo a linha norte/sul (azimute ou rumo) A orientação pode ser verdadeira (norte verdadeiro ou meridiano do elipsoide) se georreferenciada ou magnética, considerando a bússola como referência. 5

Para calcular os azimutes dos alinhamentos ou lados de uma poligonal que forma as divisas de um terreno, a partir dos ângulos formados entre esses alinhamentos medidos no campo, é necessário medir também um azimute inicial (primeiro lado ou alinhamento da poligonal.

CÁLCULO DE AZIMUTES Soma-se ao azimute inicial os ângulos à direita formado entre os alinhamentos quetanto podem ser internos ou externos, dependendo do sentido do caminhamento e o resultado, se for maior do que 360º, tira-se os 360º, em seguida verifica se o resultado é maior ou menor do que 180º; se for maior do que 180º, tirar 180º e se for menor do que 180º, soma-se 180º e o resultado é o azimute do alinhamento seguinte: 8

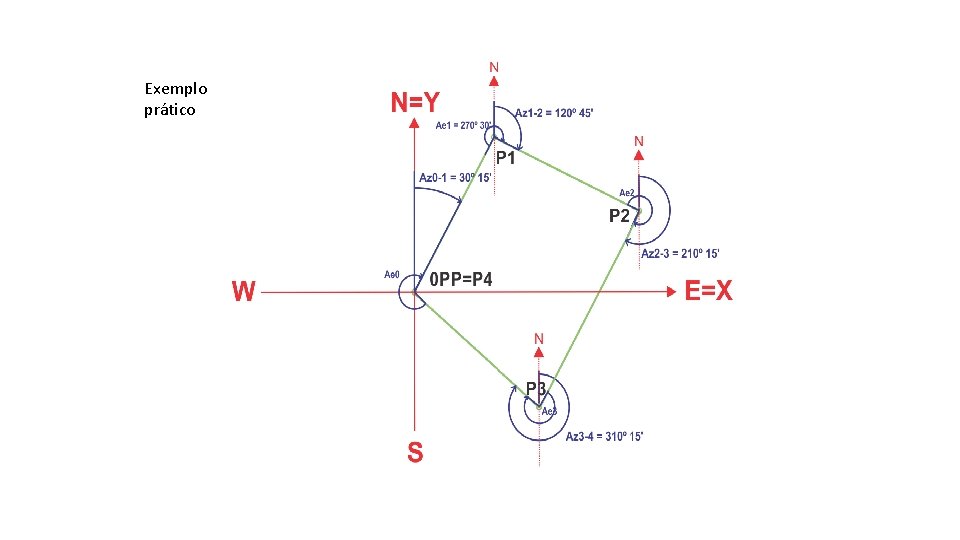
Exemplo prático

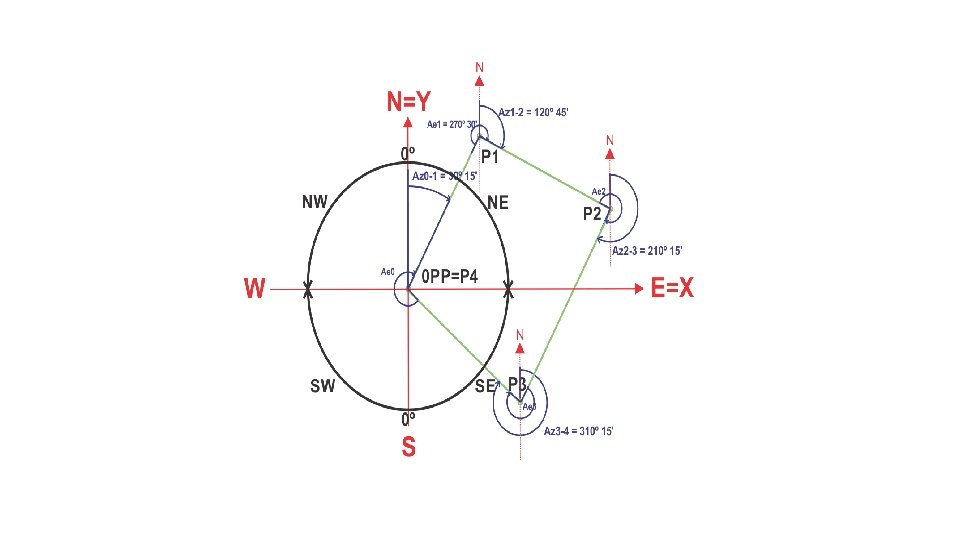
A partir do azimute inicial Az 0 -1 são calculados os azimutes dos alinhamentos subsequentes utilizando o ângulo formado pelo alinhamento anterior e o alinhamento seguinte. Os 3 passos a seguir servem para caso.

1º passo: somar Az 0 -1 com Ae 1 = 30º 15’ + 270º 30’ = 300º 45’; 2º passo: Verificar se a soma passou de 360º, se passar, tirar 360º; 3º passo: Verificar se o resultado da soma é maior ou menor do que 180º: no caso é maior; portanto tiro 180º e o resultado é o azimute do alinhamento Az 0 -1 = 120º 45’. 11

Importante: observar que o primeiro e o terceiro sempre existem, o segundo só existe se a primeira soma passar de 360º. Os demais azimutes na sequência de uma poligonal são calculados sempre seguindo esses três passos que valem para qualquer situação 12

CÁLCULO DE RUMOS São ângulos gerados entre a direção norte ou sul e a direção do alinhamento. Rumos tem por origem a direção norte ou sul. Importante: 0° ≤ R ≤ 90°

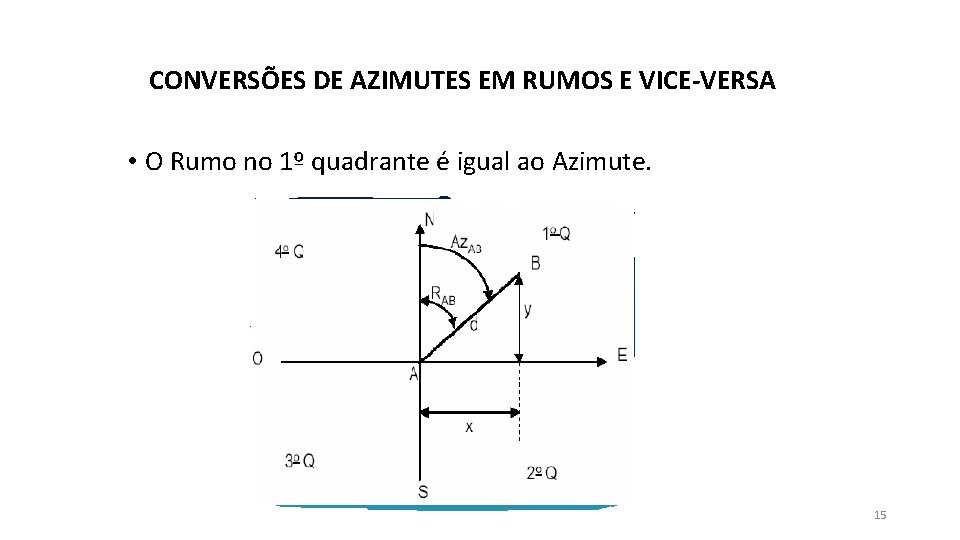
CONVERSÕES DE AZIMUTES EM RUMOS E VICE-VERSA • O Rumo no 1º quadrante é igual ao Azimute. 15

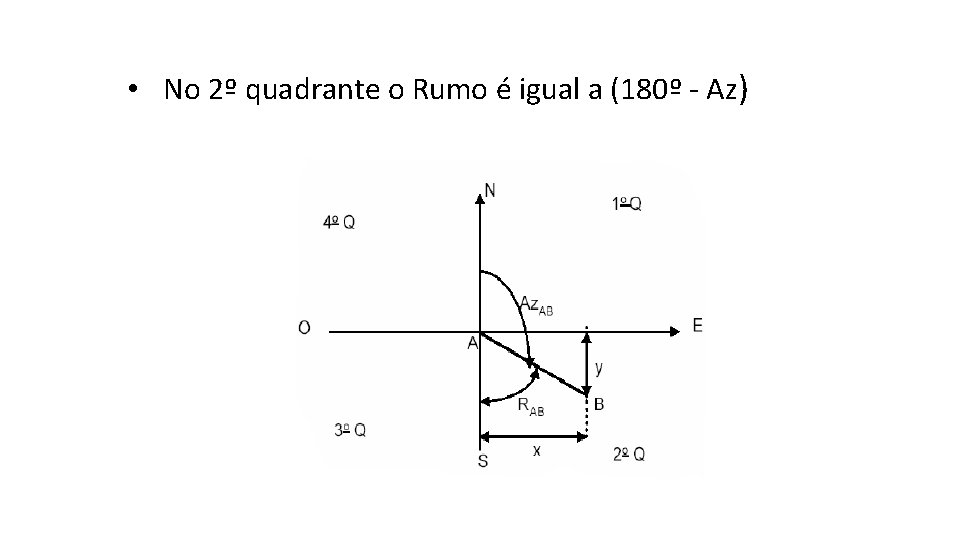
• No 2º quadrante o Rumo é igual a (180º - Az)

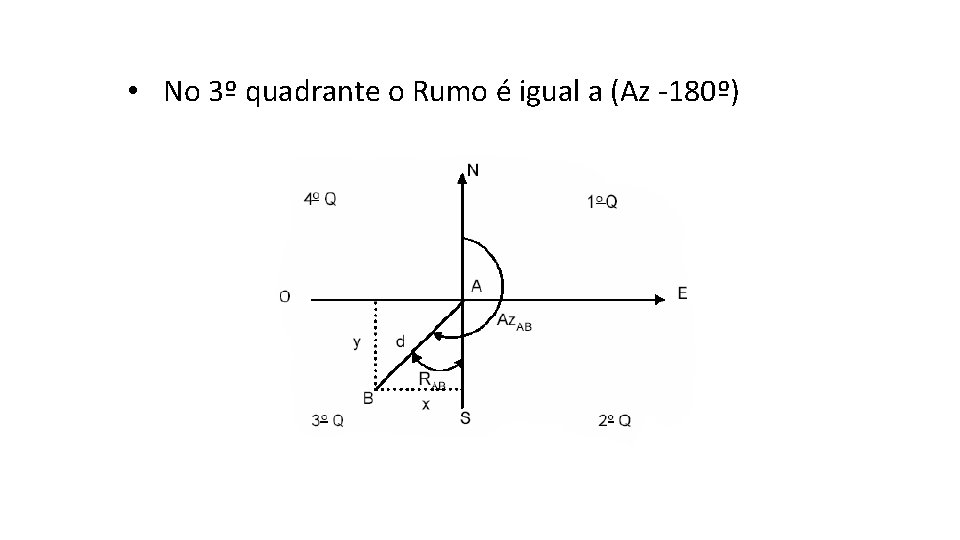
• No 3º quadrante o Rumo é igual a (Az -180º)

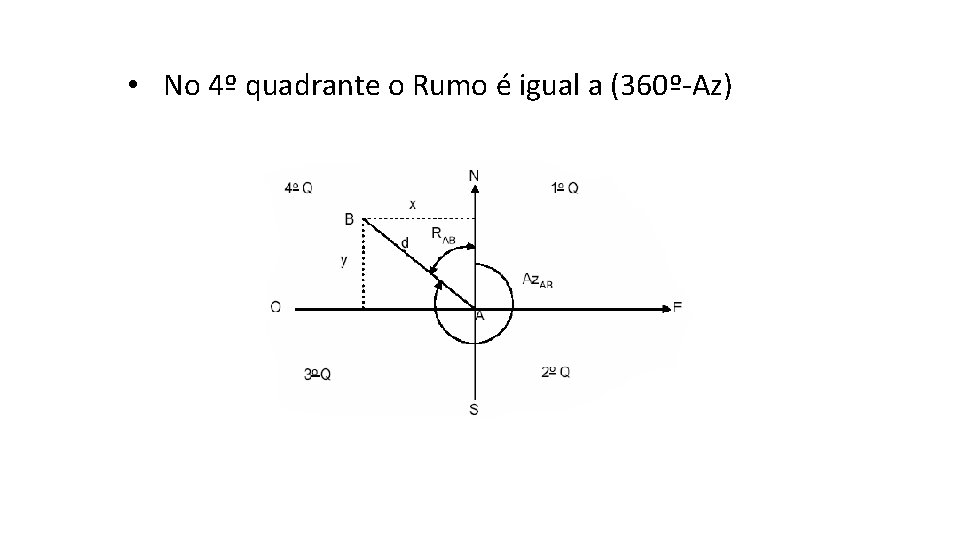
• No 4º quadrante o Rumo é igual a (360º-Az)

TRANSFORMANDO AZIMUTES EM RUMOS • • 1 o Quadrante: Rumo = Azimute 2 o Quadrante: Rumo = 180º – Azimute 3 o Quadrante: Rumo = Azimute – 180º 4 o Quadrante: Rumo = 360º - Azimute

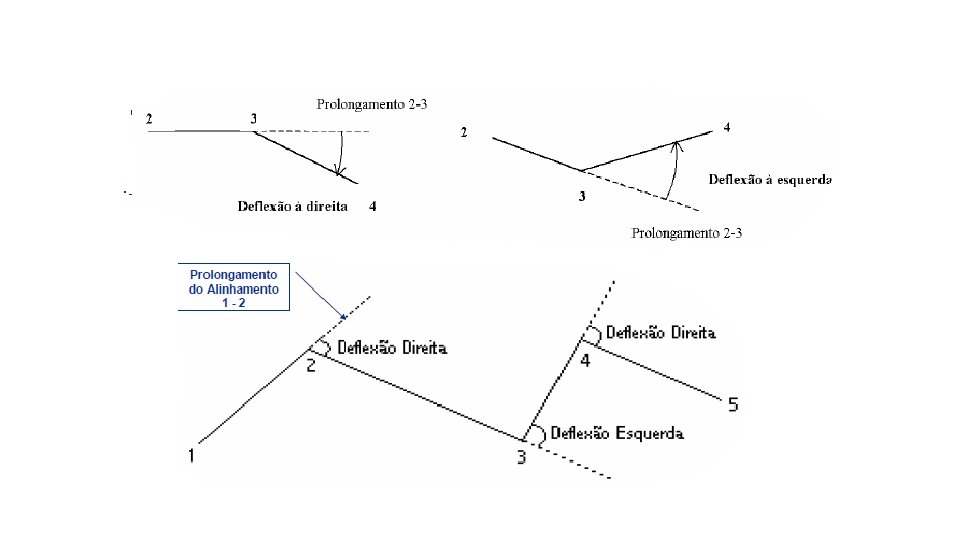
RUMO - ngulo de Deflexão É o ângulo formado pelo prolongamento do alinhamento anterior do caminhamento e o novo alinhamento. Podem ter sentido a direita ou a esquerda, conforme a direção do novo alinhamento e Varia entre 0º e 180º.

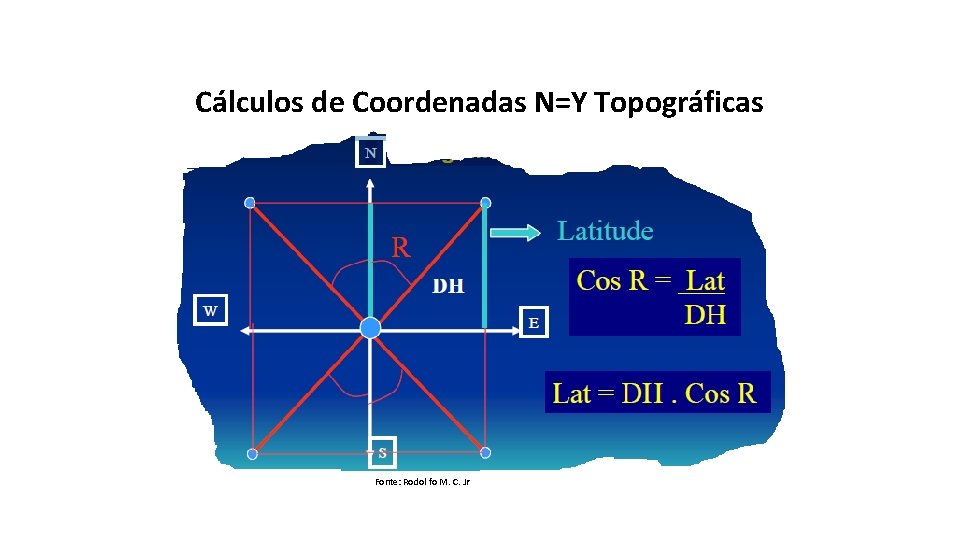
Cálculos de Coordenadas N=Y Topográficas Fonte: Rodol fo M. C. Jr

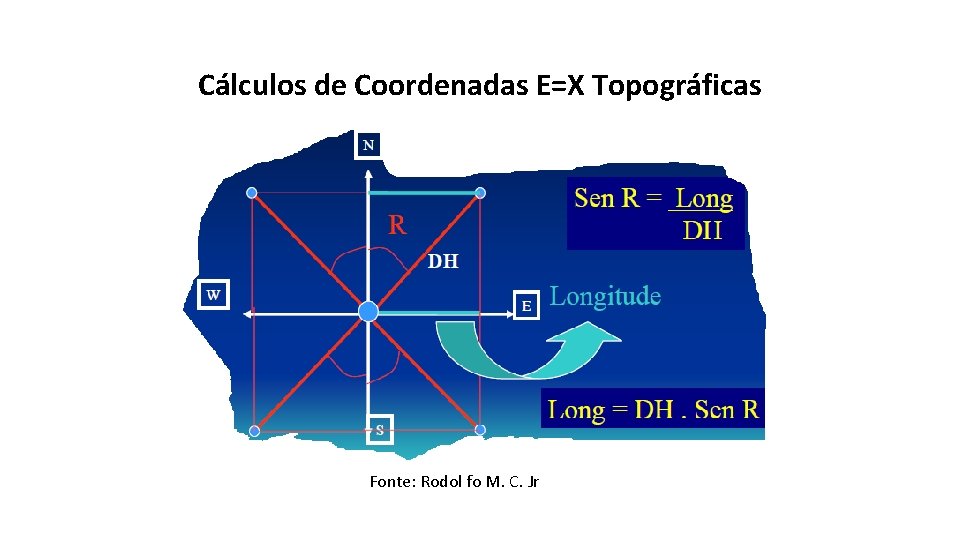
Cálculos de Coordenadas E=X Topográficas Fonte: Rodol fo M. C. Jr