AULA 13 Fernando Luiz Pellegrini Pessoa TPQBq ESCOLA

AULA 13 Fernando Luiz Pellegrini Pessoa TPQBq ESCOLA DE QUÍMICA UNIVERSIDADE FEDERAL DO RIO DE JANEIRO

Teste de Consistência TD Para dados de ELV ter a consistência assegurada, a equação básica deve ser satisfeita pelos dados experimentais. experimental data. Equação Gibbs-Duhem:

Teste Van Ness-Byer-Gibbs Cálculo de coef. de atividades a partir de dados binários ELV Se tem o modelo para o coef. de atividade então se pode calcular ELV (considerando a fase vapor ideal): – Fixar a fração molar da fase líquida. Para uma mistura binária pode-se começar com x 1 = 0 e passo a apssao vai até x 1= 1. – Cálcula a pressão total: – Cálcula a fração molar da fase vapor: Este processo pode ser invertido para calcular os coef. de atividadee G em excesso.

Cálculo do coef. de atividade a partir de 1. Ler dados Pxy em Excel ou Matlab ou outro programa. Então calcule osdados valores dede 1 para cada ponto, ELV 2. Calcule ln 1 e então calcule GE/RT 3. Pode ser útil calcular GE/x 1 x 2 RT para uma mistura binária. Fazer os gráficos de ln 1 , GE/RT, e GE/x 1 x 2 RT versus x 1.

Ajuste de dados ELV para um modelo de coef. atividade. 1. Considere a forma funcional para GE/RT. Por exemplo, usar as equações de Margules,

2. Ajuste de dados experimentais para modelos pode ser feito da seguinte maneira: Ajustar os dados GE/x 1 x 2 RT com o modelo para achar os parâmetros. Em geral, não-linear. Equação de Margules para GE/x 1 x 2 RT é linear em x 1 , regressão linear. 1. Estimativa inicial para parâmetros. 2. Construir função objetivo para ser minimizada da forma:

onde N é o número de pontos e X 1, i é a fração molar de 1 no ponto i. 3. Usar um programa (Excel Solver) para encontrar os valores dos parâmetros.

2. Método de Barker - dados P - T- x
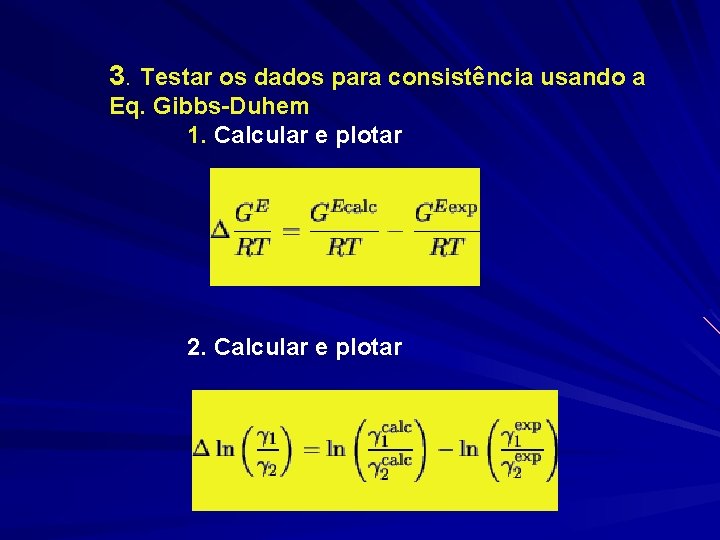
3. Testar os dados para consistência usando a Eq. Gibbs-Duhem 1. Calcular e plotar 2. Calcular e plotar

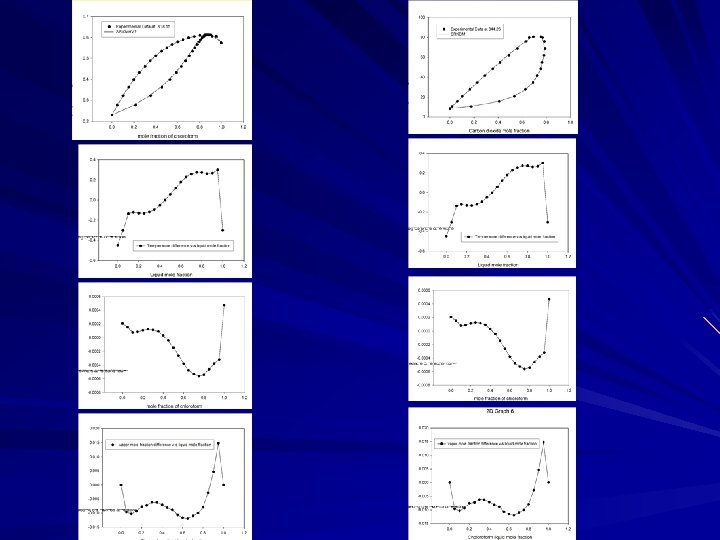
3. Se os valores de GE/RT estão em torno de zero então ln( 1/ 2) é uma medida válida dos desvios da eq. de Gibbs-Duhem. Se os dados não estão distribuídos em torno de zero, isto é, se existe algum erro em ln( 1/ 2) versus x 1 mostra algum desvio sistemático então o modelo não pode ajustar os dados e não se pode dizer alguma coisa sobre a consistência dos dados. 4. Calcular o desvio médio absoluto

Onde N é o número de pontos. Se AAD for menor ou igual a 0. 03 então os dados são altamente consistente. Se AAD 0. 1 os dados são provavelmente consistentes, e se AAD 0. 1 são provavelmente não consistente.

As inconsistências termodinâmicas são devidas às considerações feitas nos cálculos dos coeficientes, aos erros inerentes dos dados experimentais, ou ambos.

Teste Integral (teste da área) Smith (1984): razão Área = 0 -0. 6 dados inaceitáveis = 0. 6 -0. 8 dados marginais = 0. 8 -0. 9 dados regulares = 0. 9 -0. 95 dados bons = 0. 95 -1. 0 dados excelentes

Teste diferencial – Uma forma conceniente para verificar se a eq. é satisfeita – F = 0 TD consistência perfeita

Teste da diluição infinita (Kojima et al. , 1990) – Uma função suave é ajustada para os valores de ln( 1/ 2) e a função é extrapolada para x 1 = 0, e x 2 =1 para obter valores do coef. de atividade a diluição infinita. – Uma função suave é ajustada para os valores de GE/RTx 1 x 2 e a função é extrapolada para x 1 = 0, e x 2 =1 para obter valores do coef. de atividade a diluição infinita. – Os dados são consistentes de os valores extrapolados concordam em 30%

A extensão do modo - desenvolvido para dados a baixas P, para a regressão de dados a altas P é um trabalho dif´cicil, por duas razões principais: 1. Na região supercrítica, o estado padrão da fase líquida é hipotético. 2. Não se pode desprezar o termo em P da eq. Gibbs-Duhem.

A última equação só é válida em baixas P. Mas em moderadas P, o lado esquerdo da primeira Eq. não pode desprezada. Bertucco et al. (1997) propuseram um novo método para testar consistência TD de dados isotérmicos ELV. EEC SRK com regra de mistura HV em P infinita e eq. Margules para calcular os coeficientes de atividades em P infinita.

- Slides: 19



































