August 30 2010 WarmupActivator Complete the Anticipation Guide




















- Slides: 30

August 30, 2010 Warm-up/Activator Complete the Anticipation Guide by making check marks in the after column.

The Fundamental Counting Principle & Tree Diagrams

The Fundamental Counting Principle • If you have 2 events: 1 event can occur m ways and another event can occur n ways, then the number of ways that both can occur is m*n • Event 1 = 4 types of meats • Event 2 = 3 types of bread • How many different types of sandwiches can you make? • 4*3 = 12

3 or more events: • 3 events can occur m, n, & p ways, then the number of ways all three can occur is m*n*p • 4 meats • 3 cheeses • 3 breads • How many different sandwiches can you make? • 4*3*3 = 36 sandwiches

• At a restaurant at Six Flags, you have the choice of 8 different entrees, 2 different salads, 12 different drinks, & 6 different desserts. • How many different dinners (one choice of each) can you choose? • 8*2*12*6= • 1152 different dinners

Fund. Counting Principal with repetition • Georgia license plates have 3 letters followed by 4 #’s. • How many different licenses plates are possible if digits and letters can be repeated? • There are 10 choices for digits and 26 choices for letters. • 26*26*26*10*10= • 175, 760, 000 different plates

Phone numbers • How many different 7 digit phone numbers are possible if the 1 st digit cannot be a 0 or 1? • 8*10*10*10= • 8, 000 different numbers

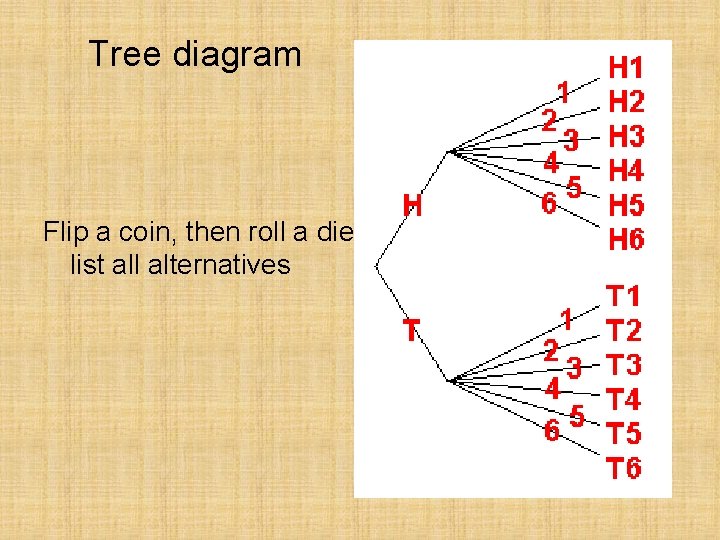
Tree diagram Flip a coin, then roll a die, list all alternatives

Simple Probability

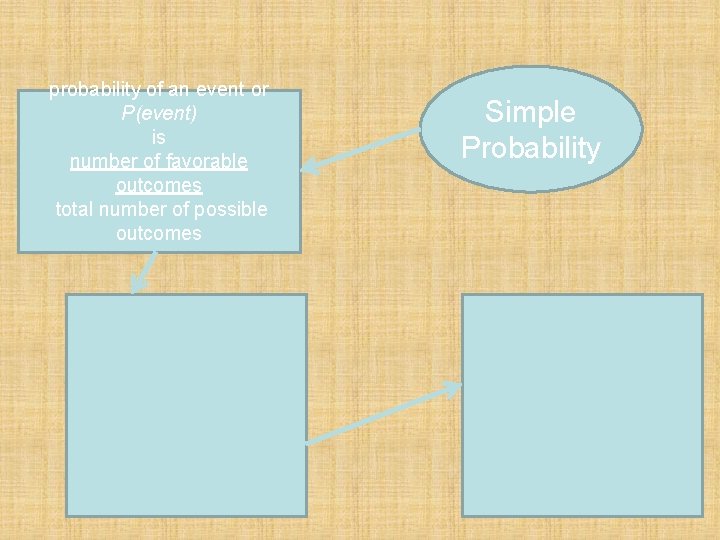
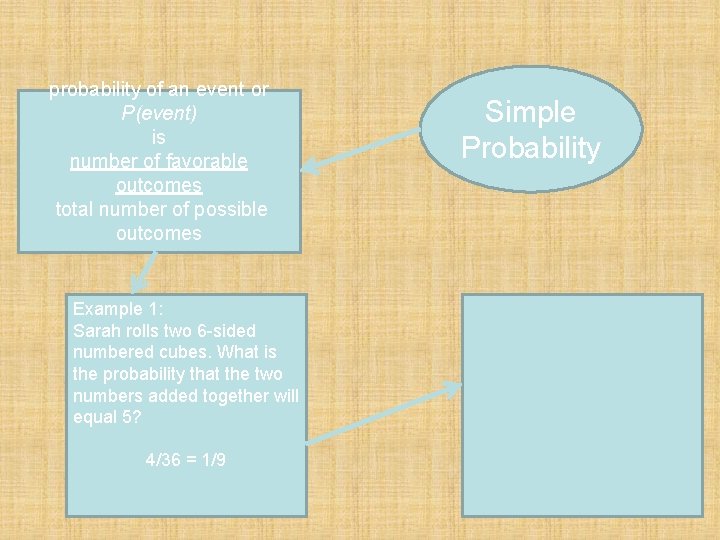
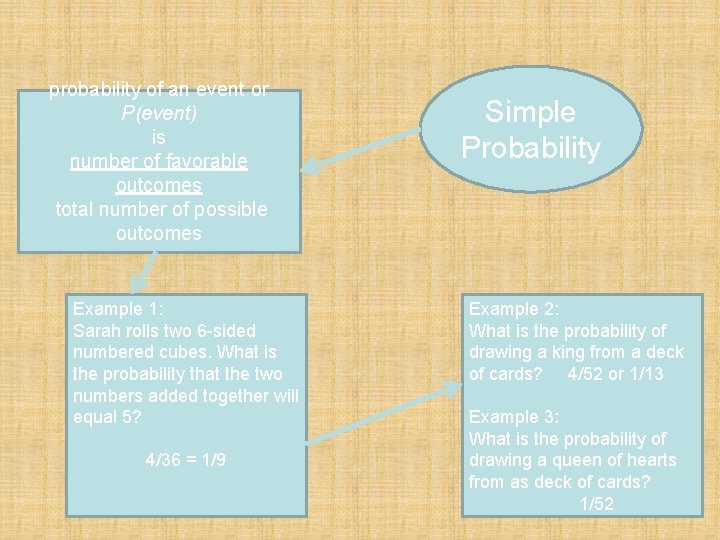
probability of an event or P(event) is number of favorable outcomes total number of possible outcomes Simple Probability

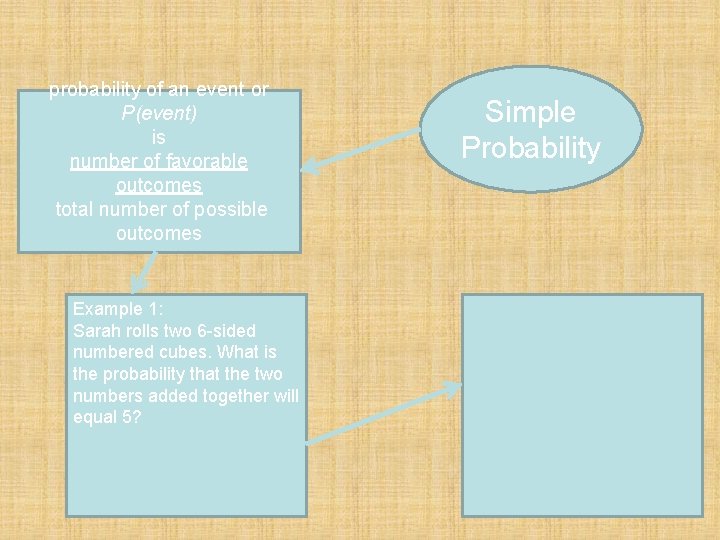
probability of an event or P(event) is number of favorable outcomes total number of possible outcomes Example 1: Sarah rolls two 6 -sided numbered cubes. What is the probability that the two numbers added together will equal 5? Simple Probability

probability of an event or P(event) is number of favorable outcomes total number of possible outcomes Example 1: Sarah rolls two 6 -sided numbered cubes. What is the probability that the two numbers added together will equal 5? 4/36 = 1/9 Simple Probability

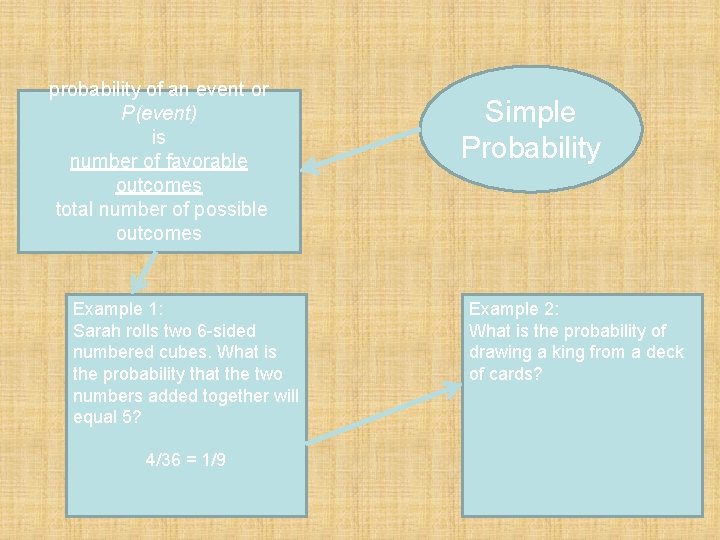
probability of an event or P(event) is number of favorable outcomes total number of possible outcomes Example 1: Sarah rolls two 6 -sided numbered cubes. What is the probability that the two numbers added together will equal 5? 4/36 = 1/9 Simple Probability Example 2: What is the probability of drawing a king from a deck of cards?

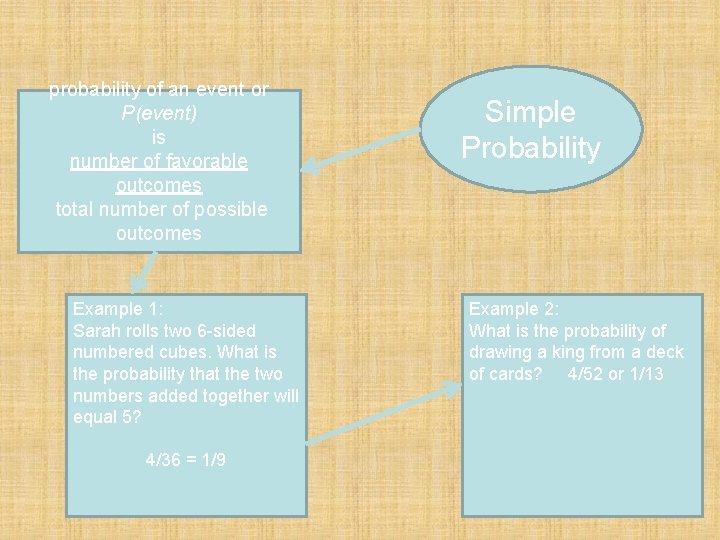
probability of an event or P(event) is number of favorable outcomes total number of possible outcomes Example 1: Sarah rolls two 6 -sided numbered cubes. What is the probability that the two numbers added together will equal 5? 4/36 = 1/9 Simple Probability Example 2: What is the probability of drawing a king from a deck of cards? 4/52 or 1/13

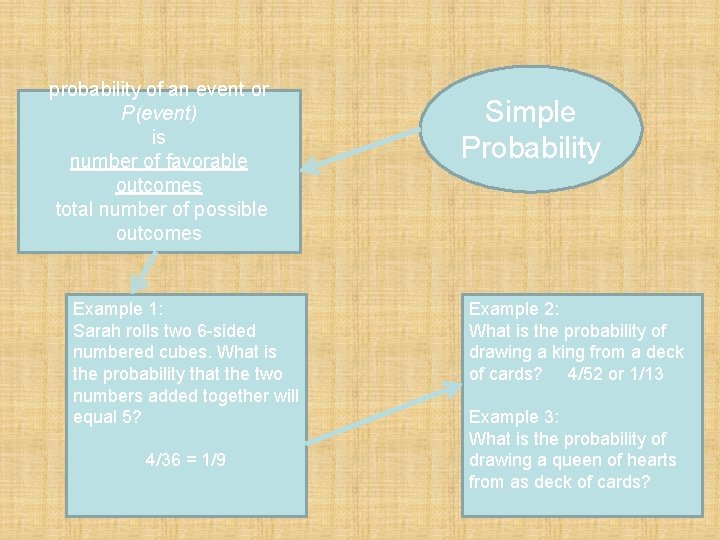
probability of an event or P(event) is number of favorable outcomes total number of possible outcomes Example 1: Sarah rolls two 6 -sided numbered cubes. What is the probability that the two numbers added together will equal 5? 4/36 = 1/9 Simple Probability Example 2: What is the probability of drawing a king from a deck of cards? 4/52 or 1/13 Example 3: What is the probability of drawing a queen of hearts from as deck of cards?

probability of an event or P(event) is number of favorable outcomes total number of possible outcomes Example 1: Sarah rolls two 6 -sided numbered cubes. What is the probability that the two numbers added together will equal 5? 4/36 = 1/9 Simple Probability Example 2: What is the probability of drawing a king from a deck of cards? 4/52 or 1/13 Example 3: What is the probability of drawing a queen of hearts from as deck of cards? 1/52


AUC


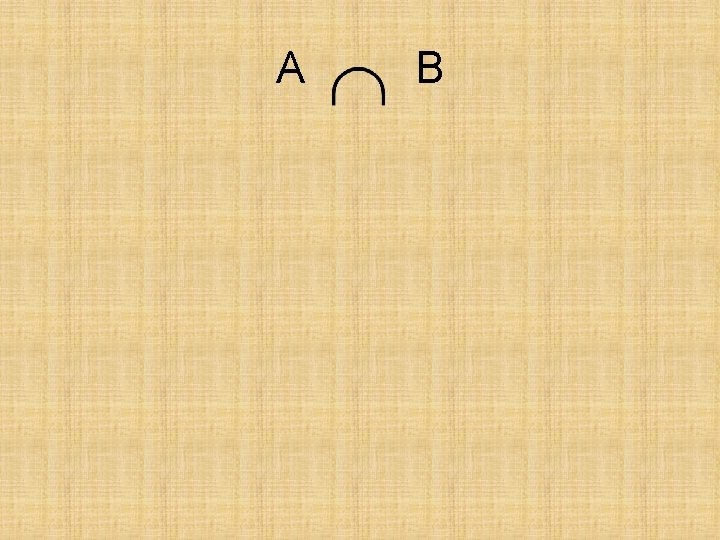
A B


A B C

Complement • The universal set includes the letters of the alphabet. Set A={consonants}. What is A’? Hint: A’ means the complement of Set A. In other words, everything that is not in Set A.

Complement • The universal set includes the letters of the alphabet. Set A={consonants}. What is A’? {vowels}

Union • What is A B if A = {m, a, t, h, e, m, a, t, i, c, s} and B = {t, h, e, o, r, y}? • - the symbol for what the two sets have together.

Union • What is A B if A = {m a t h e m a t i c s} and B = {t h e o r y}? • {t h e o r y m a i c s}

Union • What is A B if A = {p, y, t, h, o, n } and B = {f, a, c, t, o, r}?

Union • What is A B if A = {p, y, t, h, o, n } and B = {f, a, c, t, o, r}? • {p, y, t, h, o, n, f, a, c, r}

Intersection • If set A = {1, 2, 3, 4, 5, 6, 7, 8} and B = {2, 4, 6, 8, 10}, what is A B? • is the symbol for what the two set share, or have in common.

Intersection • If set A = {1, 2, 3, 4, 5, 6, 7, 8} and B = {2, 4, 6, 8, 10}, what is A B? • {2, 4, 6, 8}