Augmenting Definitive Screening Designs for Estimating Quadratic Models
























- Slides: 36

Augmenting Definitive Screening Designs for Estimating Quadratic Models Abigael C. Nachtsheim Research Training Group 2017 SCHOOL OF MATHEMATICAL AND STATISTICAL SCIENCES

Motivating Example: Laser Etching SCHOOL OF MATHEMATICAL AND STATISTICAL SCIENCES Abigael C. Nachtsheim 2

Motivating Example: Laser Etching • Screening experiment • 6 factors, line width, pulse rate, scan speed, laser power, height, color • Response: etch clarity SCHOOL OF MATHEMATICAL AND STATISTICAL SCIENCES Abigael C. Nachtsheim 3

Motivating Example: Laser Etching SCHOOL OF MATHEMATICAL AND STATISTICAL SCIENCES Abigael C. Nachtsheim 4

Motivating Example: Laser Etching • Screening experiment • 6 factors, line width, pulse rate, scan speed, laser power, height, color • Response: etch clarity • The experimenter wants to use a Definitive Screening Design (DSD) SCHOOL OF MATHEMATICAL AND STATISTICAL SCIENCES Abigael C. Nachtsheim 5

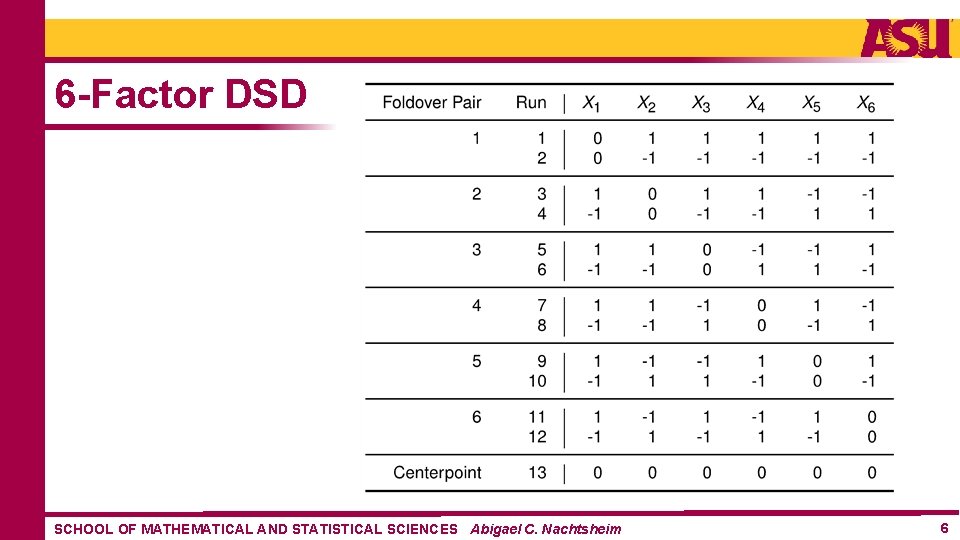
6 -Factor DSD SCHOOL OF MATHEMATICAL AND STATISTICAL SCIENCES Abigael C. Nachtsheim 6

Why a DSD? • Small number of runs required SCHOOL OF MATHEMATICAL AND STATISTICAL SCIENCES Abigael C. Nachtsheim 7

Why a DSD? • Small number of runs required • Orthogonal for main effects SCHOOL OF MATHEMATICAL AND STATISTICAL SCIENCES Abigael C. Nachtsheim 8

Why a DSD? • Small number of runs required • Orthogonal for main effects • Foldover pairs result in statistical independence of main effects and two-factor interactions SCHOOL OF MATHEMATICAL AND STATISTICAL SCIENCES Abigael C. Nachtsheim 9

Why a DSD? • Small number of runs required • Orthogonal for main effects • Foldover pairs result in statistical independence of main effects and two-factor interactions • Second-order effects not completely confounded with other second-order effects SCHOOL OF MATHEMATICAL AND STATISTICAL SCIENCES Abigael C. Nachtsheim 10

Why a DSD? • Small number of runs required • Orthogonal for main effects • Foldover pairs result in statistical independence of main effects and two-factor interactions • Second-order effects not completely confounded with other second-order effects • 3 -level design: all quadratic effects are estimable SCHOOL OF MATHEMATICAL AND STATISTICAL SCIENCES Abigael C. Nachtsheim 11

However… • If the number of active effects is less than n/2, the estimated model form is probably right • If not, the model is probably wrong Need to augment the design to find the right second-order model! *Errore, Jones, Li, and Nachtsheim, Journal of Quality Technology, 2017 SCHOOL OF MATHEMATICAL AND STATISTICAL SCIENCES Abigael C. Nachtsheim 12

Today’s Plan 1) Show to augment DSDs 2) Perform a simulation study to evaluate the augmented designs 3) Conclusions SCHOOL OF MATHEMATICAL AND STATISTICAL SCIENCES Abigael C. Nachtsheim 13

Two Possible Goals 1) Estimation -correctly identify active model terms SCHOOL OF MATHEMATICAL AND STATISTICAL SCIENCES Abigael C. Nachtsheim 14

Two Possible Goals 1) Estimation -correctly identify active model terms 2) Prediction -precise estimation of responses SCHOOL OF MATHEMATICAL AND STATISTICAL SCIENCES Abigael C. Nachtsheim 15

Two Possible Goals 1) Estimation Previous work -correctly identify active model terms 2) Prediction -precise estimation of responses SCHOOL OF MATHEMATICAL AND STATISTICAL SCIENCES Abigael C. Nachtsheim 16

Two Possible Goals 1) Estimation -correctly identify active model terms 2) Prediction Today’s focus -precise estimation of responses SCHOOL OF MATHEMATICAL AND STATISTICAL SCIENCES Abigael C. Nachtsheim 17

Approach 1: Response Surface Design (RSD) • Augment to obtain a (equivalent of) response surface design • Classical design---widely used for prediction • Most expensive approach - 6 -factor central composite response surface design requires 46 runs SCHOOL OF MATHEMATICAL AND STATISTICAL SCIENCES Abigael C. Nachtsheim 18

Approach 2: Saturated Design (SD) • Saturated designs are the smallest designs that allow estimation of all possible effects for the model of interest • For full quadratic model, n = (m+1)(m+2)/2 • For m = 6, n = 28. • Intermediate cost SCHOOL OF MATHEMATICAL AND STATISTICAL SCIENCES Abigael C. Nachtsheim 19

Approach 3: Supersaturated Design • Designs with sample size less than the number of terms in the model of interest: n < p • DSDs are supersaturated designs for the full quadratic model • We will examine small augmentations such that the result is still a supersaturated design SCHOOL OF MATHEMATICAL AND STATISTICAL SCIENCES Abigael C. Nachtsheim 20

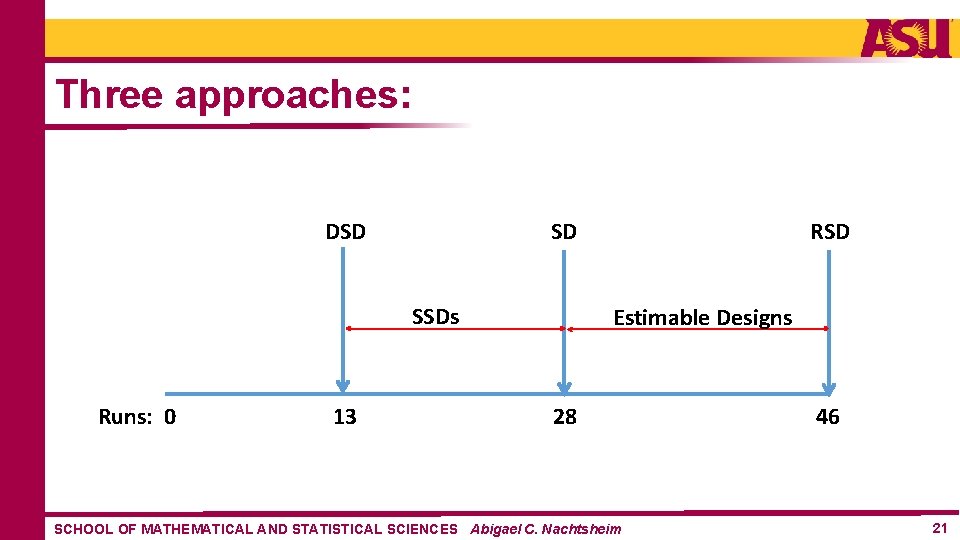
Three approaches: DSD SD SSDs Runs: 0 13 RSD Estimable Designs 28 SCHOOL OF MATHEMATICAL AND STATISTICAL SCIENCES Abigael C. Nachtsheim 46 21

Design Construction and Evaluation 1) Construct a series of augmented designs 2) Perform simulation study to calculate predictive mean square error for each design 3) Determine the number of augmented runs necessary to effectively fit the correct model SCHOOL OF MATHEMATICAL AND STATISTICAL SCIENCES Abigael C. Nachtsheim 22

Background: Design Augmentation • Collect data at naug additional points, having already collected data at n points • Where do we place these points? • Various methods exist - Dykstra (1971), Galil and Kiefer (1980), - We focus on: Bayesian I-optimal and Bayesian Doptimal augmentation Du. Mouchel and Jones (1994) SCHOOL OF MATHEMATICAL AND STATISTICAL SCIENCES Abigael C. Nachtsheim 23

Bayesian I-optimality Criterion: Minimize where M is the moment matrix and where p is the number of terms in the full quadratic model SCHOOL OF MATHEMATICAL AND STATISTICAL SCIENCES Abigael C. Nachtsheim 24

Bayesian D-optimality Criterion: Maximize SCHOOL OF MATHEMATICAL AND STATISTICAL SCIENCES Abigael C. Nachtsheim 25

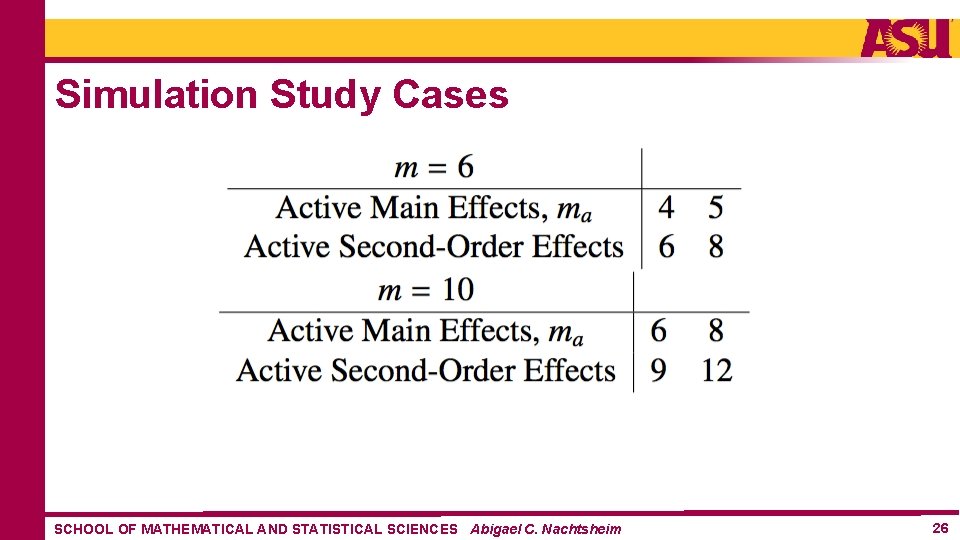
Simulation Study Cases SCHOOL OF MATHEMATICAL AND STATISTICAL SCIENCES Abigael C. Nachtsheim 26

Simulation Study Step 1: Choose active effects at random Step 2: Generate nonzero beta coefficients having signal to noise ratio greater than 3 Step 3: Generate the sign of the coefficient at random Step 4: Compute the response vector Y = Xβ + ε where ε = standard normal errors SCHOOL OF MATHEMATICAL AND STATISTICAL SCIENCES Abigael C. Nachtsheim 27

Simulation Study Analysis For each of 100 response vectors: • Employ forward selection with the AICc criterion to select the model • Compute the MSE SCHOOL OF MATHEMATICAL AND STATISTICAL SCIENCES Abigael C. Nachtsheim 28

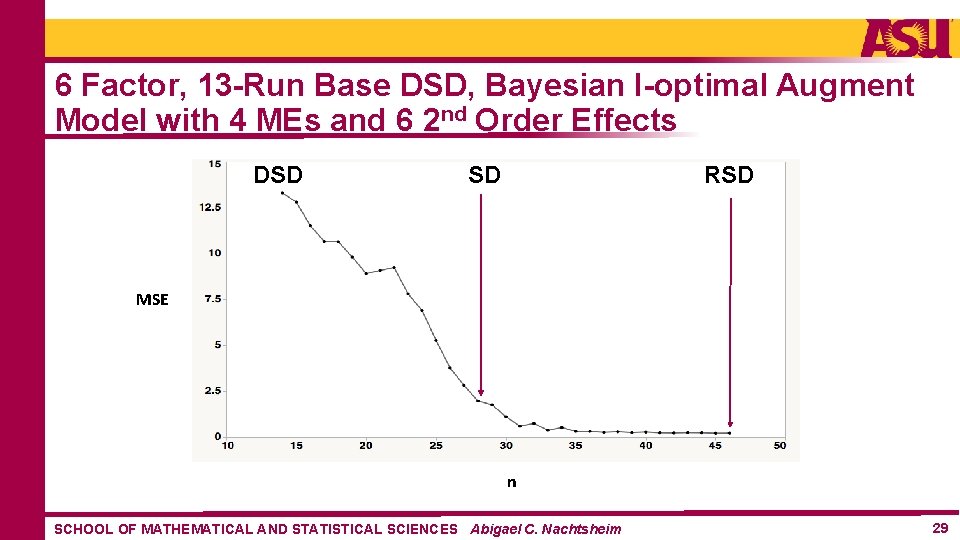
6 Factor, 13 -Run Base DSD, Bayesian I-optimal Augment Model with 4 MEs and 6 2 nd Order Effects DSD RSD SD MSE n SCHOOL OF MATHEMATICAL AND STATISTICAL SCIENCES Abigael C. Nachtsheim 29

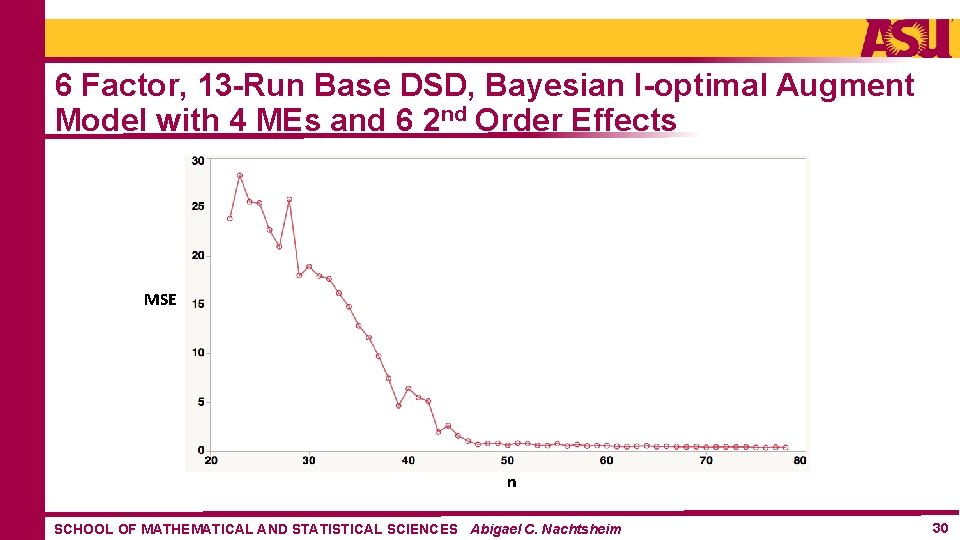
6 Factor, 13 -Run Base DSD, Bayesian I-optimal Augment Model with 4 MEs and 6 2 nd Order Effects MSE n SCHOOL OF MATHEMATICAL AND STATISTICAL SCIENCES Abigael C. Nachtsheim 30

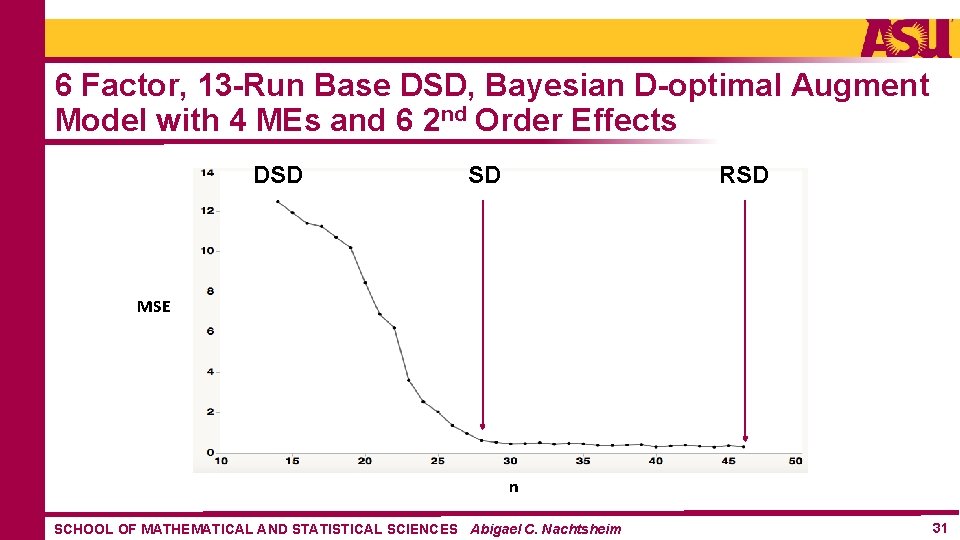
6 Factor, 13 -Run Base DSD, Bayesian D-optimal Augment Model with 4 MEs and 6 2 nd Order Effects DSD RSD SD MSE n SCHOOL OF MATHEMATICAL AND STATISTICAL SCIENCES Abigael C. Nachtsheim 31

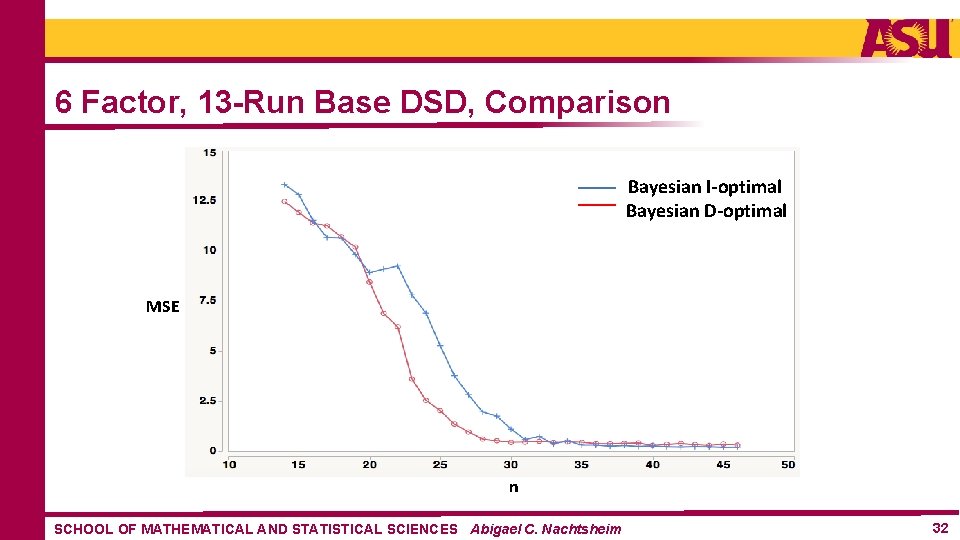
6 Factor, 13 -Run Base DSD, Comparison Bayesian I-optimal Bayesian D-optimal MSE n SCHOOL OF MATHEMATICAL AND STATISTICAL SCIENCES Abigael C. Nachtsheim 32

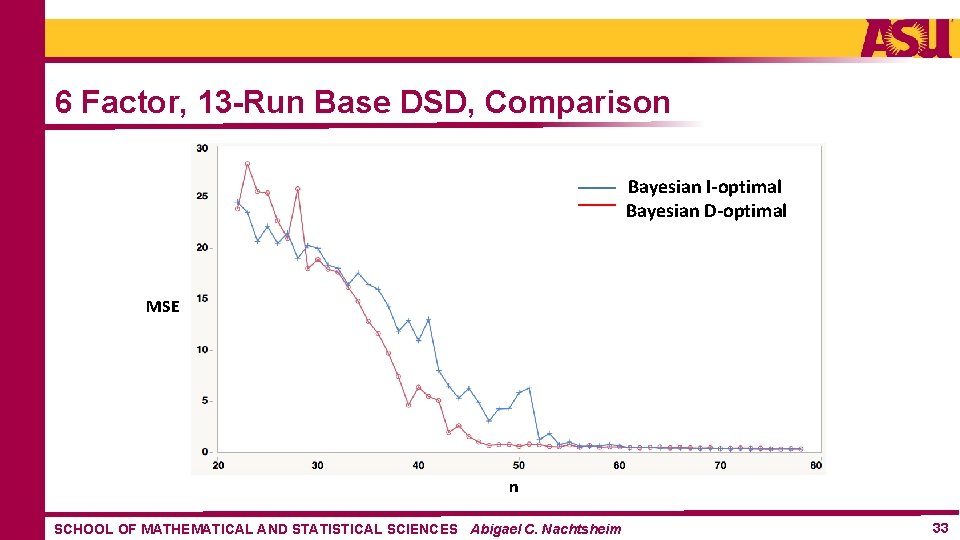
6 Factor, 13 -Run Base DSD, Comparison Bayesian I-optimal Bayesian D-optimal MSE n SCHOOL OF MATHEMATICAL AND STATISTICAL SCIENCES Abigael C. Nachtsheim 33

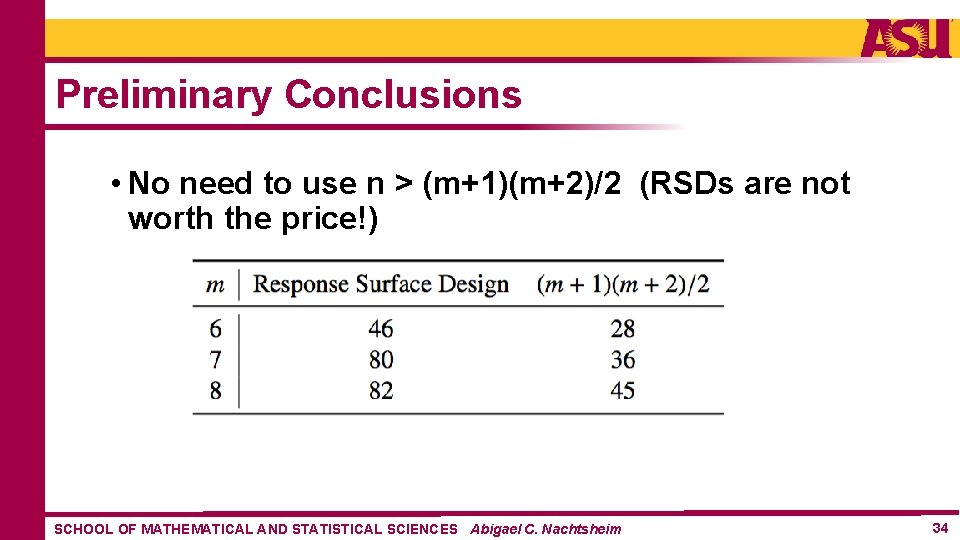
Preliminary Conclusions • No need to use n > (m+1)(m+2)/2 (RSDs are not worth the price!) SCHOOL OF MATHEMATICAL AND STATISTICAL SCIENCES Abigael C. Nachtsheim 34

Preliminary Conclusions • No need to use n > (m+1)(m+2)/2 (RSDs are not worth the price!) • Bayesian D-optimal designs appear to be superior to Bayesian I-optimal designs SCHOOL OF MATHEMATICAL AND STATISTICAL SCIENCES Abigael C. Nachtsheim 35

Future work 1) More extensive simulation study involving - Different numbers of factors - Different model selection approaches (e. g. , Dantzig, Lasso) - Different levels of sparsity (true models) 2) Evaluate the effect of augmentation on MSE for sparse models 3) Incorporate into previous work SCHOOL OF MATHEMATICAL AND STATISTICAL SCIENCES Abigael C. Nachtsheim 36