Attribute Grammars Attribute Grammar is a Framework for

Attribute Grammars Attribute Grammar is a Framework for specifying semantics and enables Modular specification. http: //knoesis. wright. edu/tkprasad/papers/Attribute-Grammars. pdf CS 784 (Prasad) L 167 AG 1
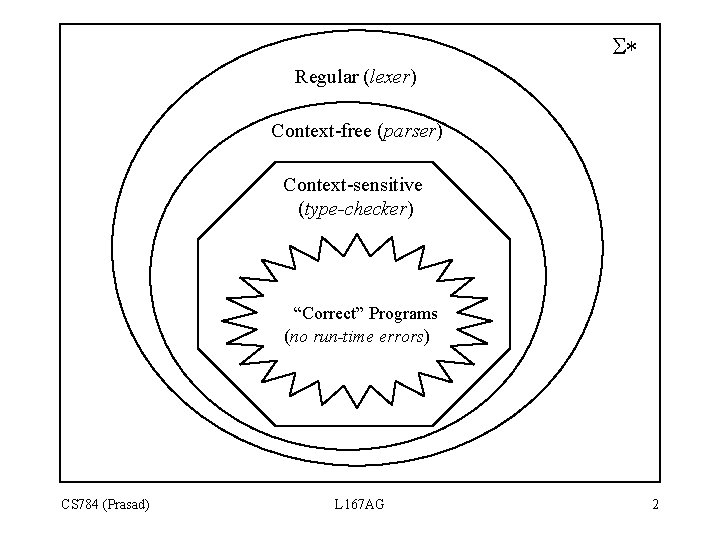
S* Regular (lexer) Context-free (parser) Context-sensitive (type-checker) “Correct” Programs (no run-time errors) CS 784 (Prasad) L 167 AG 2

Semantics of Bit Pattern : 0101110 . • ASCII Character “ ” • Number • Switch positions – 46 (if base 2) – 101110 (if base 10) – ON-OFF-ON-… • Fraction • Binary string “ 0101110” – 23/64 • Unary encoding “ 13” CS 784 (Prasad) L 167 AG 3

Motivation for Precise Specification • Capture subtly different semantics for the same syntax in various languages. § Arrays and strings. § Parameter passing mechanisms. § Scoping rules. § Primitive types vs Composite types. § Type equivalence. CS 784 (Prasad) L 167 AG 4

Attribute Grammars Formalism for specifying semantics based on context-free grammars (BNF) © Static semantics (context-sensitive aspects) • Type checking and type inference • Compatibility between procedure definition and call • Scope rules © Dynamic semantics • Associate attributes with terminals and non-terminals • Associate attribute computation rules with productions CS 784 (Prasad) L 167 AG 5

Synthesized Attributes ª N -> 0 N. val : = 0 ª N -> 1 N. val : = 1 ª N -> N 0 N. val : = 2* N. val ª N -> N 1 N. val : = 2* N. val + 1 CS 784 (Prasad) L 167 AG 6
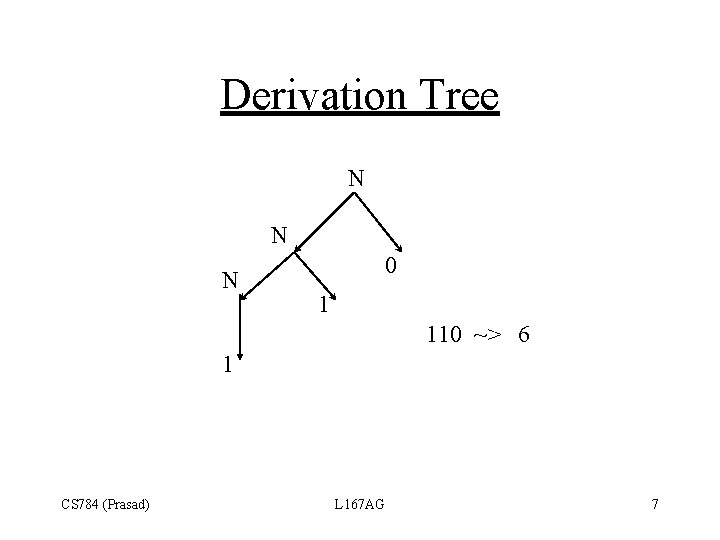
Derivation Tree N N N 0 1 110 ~> 6 1 CS 784 (Prasad) L 167 AG 7

Synthesized Attributes N. val : = 0 N. len : = 1 ª N -> 0 ª N -> 1 N. val : = 1 N. len : = 1 ª N -> 0 N N. val : = N. val N. len : = N. len + 1 ª N -> 1 N CS 784 (Prasad) N. val : = N. val + 2^ N. len : = N. len + 1 L 167 AG 8

Inherited Attributes • Declaration and Use { int i, j, k; i : = i + j; } <assign-stm> -> <var> : = <expr> <var>. env : = <assign-stm>. env <expr>. env : = <assign-stm>. env CS 784 (Prasad) L 167 AG 9

Inherited Attributes • Coercion Code Generation 5. 0 + 2 coerce_int_to_real • Determination of un-initialized variables • Determination of reachable non-terminals • Evaluation of an expression containing variables CS 784 (Prasad) L 167 AG 10

• Attributes – Synthesized – Inherited A(X) S(X) I(X) • Attribute computation rules (Semantic functions) X 0 -> X 1 X 2 … Xn S(X 0) = f( I(X 0), A(X 1), A(X 2), …, A(Xn) ) I(Xj) = Gj( I(X 0), A(X 1), A(X 2), …, A(Xj-1)) for all j in 1. . n P( A(X 0), A(X 1), A(X 2), …, A(Xn) ) CS 784 (Prasad) L 167 AG 11
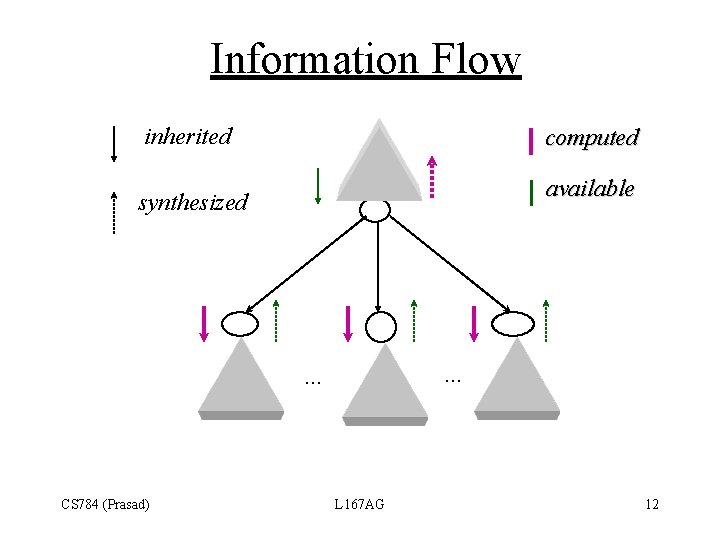
Information Flow inherited computed available synthesized . . . CS 784 (Prasad) L 167 AG 12

• Synthesized Attributes Pass information up the parse tree • Inherited Attributes Pass information down the parse tree or from left siblings to the right siblings • Attribute values assumed to be available from the context. • Attribute values computed using the semantic rules provided. The constraints on the attribute evaluation rules permit top-down left-to-right (one-pass) traversal of the parse tree to compute the meaning. CS 784 (Prasad) L 167 AG 13

Static Semantics E -> n | m E. type : = int E -> x | y E. type : = real E -> E 1 + E 2 E -> E 1 * E 2 CS 784 (Prasad) if E 1. type = E 2. type then E. type : = E 1. type else E. type : = real L 167 AG 14

Executable Specification in Prolog type(i, int). type(x, real). type(+(E, F), T) : - type(E, T), type(F, T). type(+(E, F), real) : - type(E, T 1), type(F, T 2), T 1 = T 2. • Type Checking ? - type(+(i, x), real). • Type Inference ? - type(+(x, x), T). CS 784 (Prasad) L 167 AG 15

Static Semantics E E -> -> n p | | E. type : = int E. type : = bool m q ( E 0. type = bool ) Ù ( E 1. type = E 2. type ) then E. type : = E 1. type else type error if E -> CS 784 (Prasad) if then else E 0 E 1 E 2 L 167 AG 16

Fractions F ->. N F. val : = N. val N. pow : = 1 N -> 0 N -> 1 N. val : = 0 : = (1/2^N. pow) N -> 0 N N. pow N. val : = 1 + N. pow : = N. val N -> 1 N N. pow N. val : = 1 + N. pow : = N. val + (1/2^N. pow) CS 784 (Prasad) L 167 AG 17

Fractions (Alternate solution) F ->. N F. val : = N. val / 2 N -> 0 N -> 1 N. val : = 0 : = 1 N -> 0 N N. val : = N. val / 2 N -> 1 N N. val : = N. val / 2 + 1 CS 784 (Prasad) L 167 AG 18

Applications of Attribute Grammars • Compiler Generation – Top-down Parsers (LL(1)) • FIRST sets, FOLLOW sets, etc – Code Generation Computations • Type, Storage determination, etc • Databases – Optimizing Bottom-up Query Evaluation (Magic Sets) • Programming and Definitions CS 784 (Prasad) L 167 AG 19

An Extended Example • Distinct identifiers in a straight-line program. BNF <exp> : : = <var> | <exp> + <exp> <stm> : : = <var> : = <exp> | <stm> ; <stm> Attributes <var> <exp> <stm> ids num • Semantics specified in terms of sets (of identifiers). CS 784 (Prasad) L 167 AG 20

<exp> : : = <var> <exp>. ids = { <var>. id } <exp> : : = <exp 1> + <exp 2> <exp>. ids = <exp>. ids U <exp>. ids <stm> : : = <var> : = <exp> <stm>. ids ={ <var>. id } U <exp>. ids <stm>. num = | <stm>. ids = : : = <stm 1> ; <stm 2> <stm 1>. ids U <stm 2>. ids <stm>. num = | <stm>. ids | CS 784 (Prasad) L 167 AG 21

Alternate approach : Using lists • Attributes envi : list of vars in preceding context envo : list of vars for following context dnum : number of new variables <exp> : : = <var> <exp>. envo = if member(<var>. id, <exp>. envi) then <exp>. envi else cons(<var>. id, <exp>. envi) CS 784 (Prasad) L 167 AG 22

Attribute Computation Rules <exp> : : = <exp 1> + <exp 2> envi envo dnum <exp 1>. envi <exp 2>. envi <exp>. envo <exp>. dnum CS 784 (Prasad) = = envi envo dnum <exp>. envi <exp 1>. envo <exp 2>. envo length(<exp>. envo) L 167 AG 23
- Slides: 23