Attenuation of Diffracted Multiples Gabriel Alvarez Biondo Biondi

Attenuation of Diffracted Multiples Gabriel Alvarez Biondo Biondi Antoine Guitton Stanford University Alvarez-Biondi-Guitton 1

Goal Introduce a method to attenuate diffracted multiples on 2 D data, based on an apex-shifted Radon transform. The method is applied in image space, in particular to Angle Domain Common Image Gathers (ADCIG). Alvarez-Biondi-Guitton 2

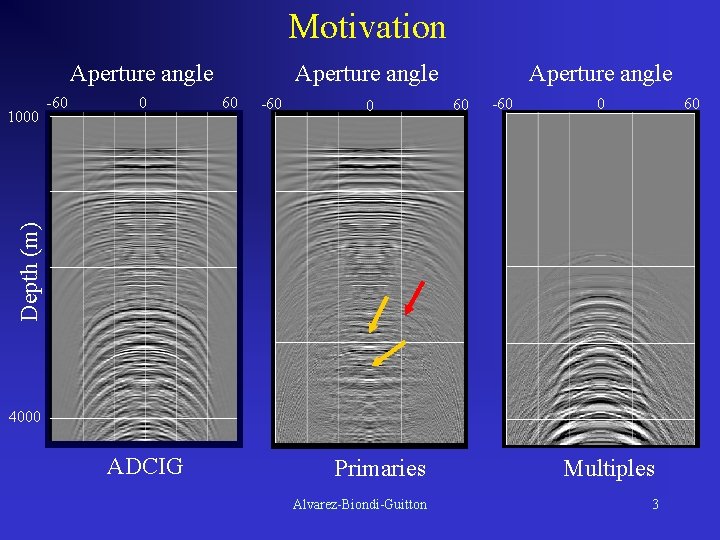
Motivation Aperture angle -60 0 60 -60 0 Aperture angle 60 -60 0 60 Depth (m) 1000 Aperture angle 4000 ADCIG Primaries Multiples Alvarez-Biondi-Guitton 3

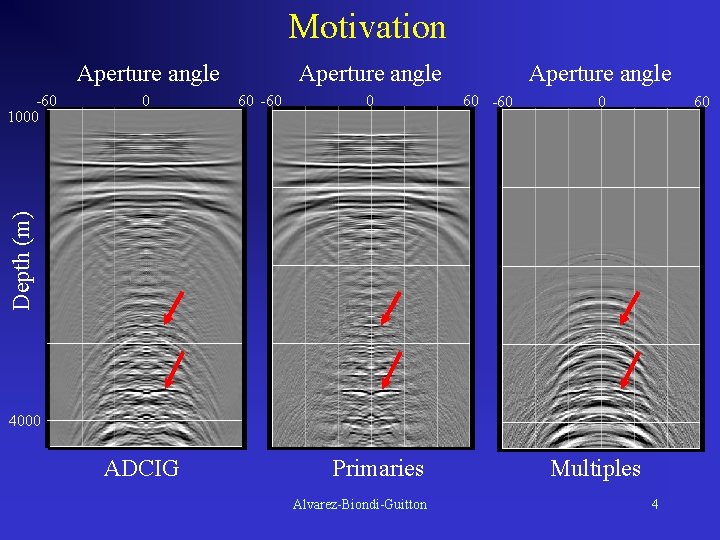
Motivation Aperture angle 0 60 -60 0 Aperture angle 60 -60 0 60 Depth (m) -60 1000 Aperture angle 4000 ADCIG Primaries Alvarez-Biondi-Guitton Multiples 4

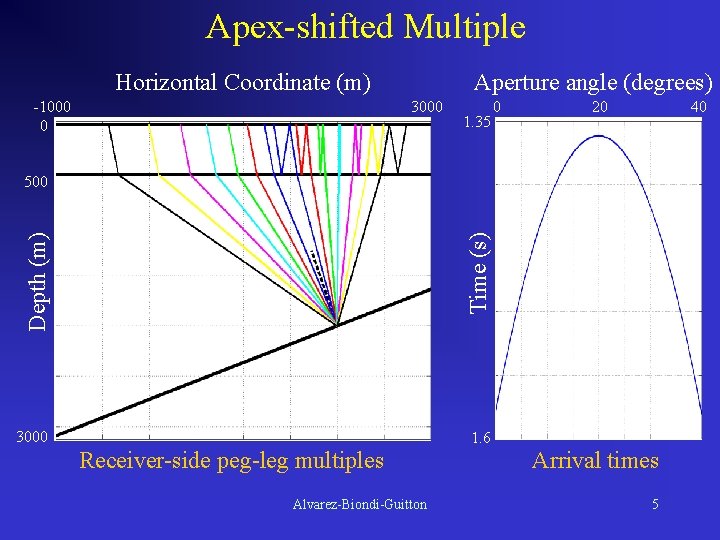
Apex-shifted Multiple Horizontal Coordinate (m) -1000 0 Aperture angle (degrees) 3000 1. 35 0 20 40 Depth (m) Time (s) 500 3000 1. 6 Receiver-side peg-leg multiples Alvarez-Biondi-Guitton Arrival times 5

A Note on Terminology Diffracted multiples: Multiples with apex-shifted residual moveout on ADCIGs migrated with primary velocity. Specularly-reflected multiples: Multiples whose residual moveout have their apex at zero aperture angle on ADCIGs migrated with primary velocity. Alvarez-Biondi-Guitton 6

What about SRME? Can Surface-Related Multiple Elimination (SRME) attenuate the apex-shifted multiples? Yes, but SRME requires dense, regular, largeaperture acquisition which is not generally available with today’s 3 D streamer geometries. An alternative: apex-shifted Radon transform of ADCIGs. Alvarez-Biondi-Guitton 7

Standard Radon Transform Aperture angle (γ) 0 Curvature (q) Primaries Depth Multiple ADCIG Alvarez-Biondi-Guitton 8

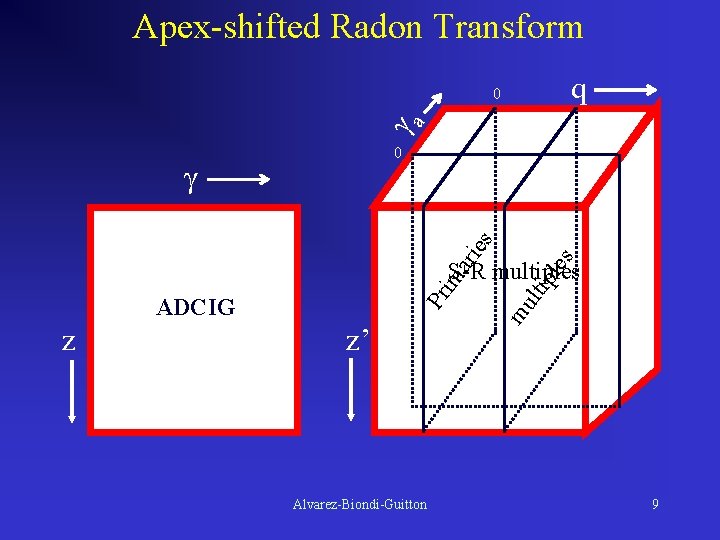
Apex-shifted Radon Transform q γa 0 0 s ari es γ z z’ Alvarez-Biondi-Guitton ple lti Pr ADCIG mu im S-R multiples 9

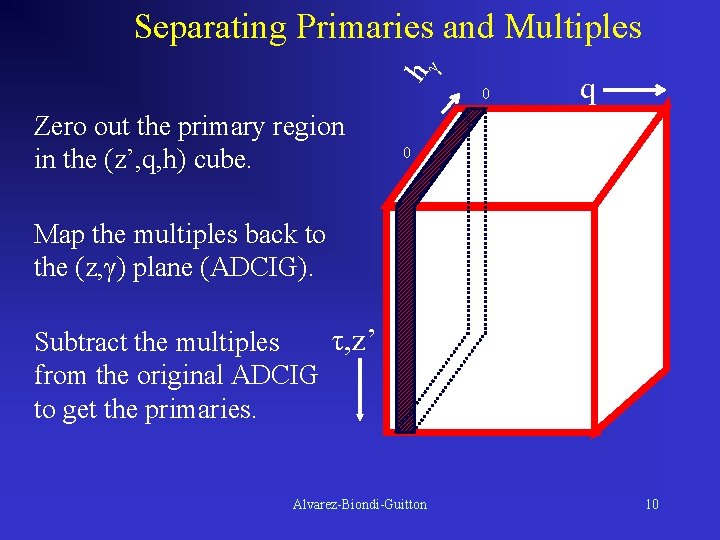
h γ Separating Primaries and Multiples 0 Zero out the primary region in the (z’, q, h) cube. q 0 Map the multiples back to the (z, γ) plane (ADCIG). τ, z’ Subtract the multiples from the original ADCIG to get the primaries. Alvarez-Biondi-Guitton 10

Image space vs. data space In complex geology the primaries are more likely to be horizontal in ADCIGs than in NMO-corrected CMPs. However In data space the multiple moveout is more intuitive (predictable)and easy to visualize. Delaying the multiple removal after imaging may compromise the choice of the migration velocities for the primaries. Alvarez-Biondi-Guitton 11

Apex-shifted Radon Transform From model space to data space (ADCIGs): γ: aperture angle q: moveout curvature γa: apex-shift distance z, z’: depth The transform is implemented as a least-squares inverse with a sparsity constraint. Alvarez-Biondi-Guitton 12

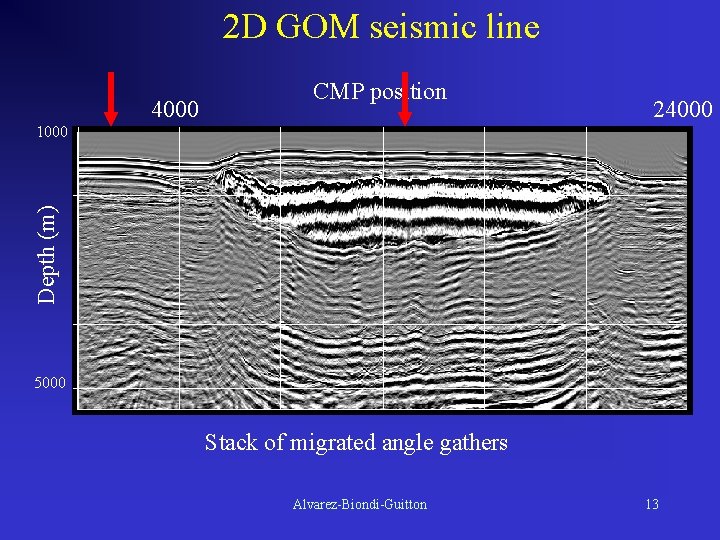
2 D GOM seismic line 4000 CMP position 24000 Depth (m) 1000 5000 Stack of migrated angle gathers Alvarez-Biondi-Guitton 13

ADCIGs Aperture-angle (degrees) 0 60 -60 1000 0 60 Depth (m) -60 1000 Aperture-angle (degrees) 5000 Sediments Below salt Alvarez-Biondi-Guitton 14

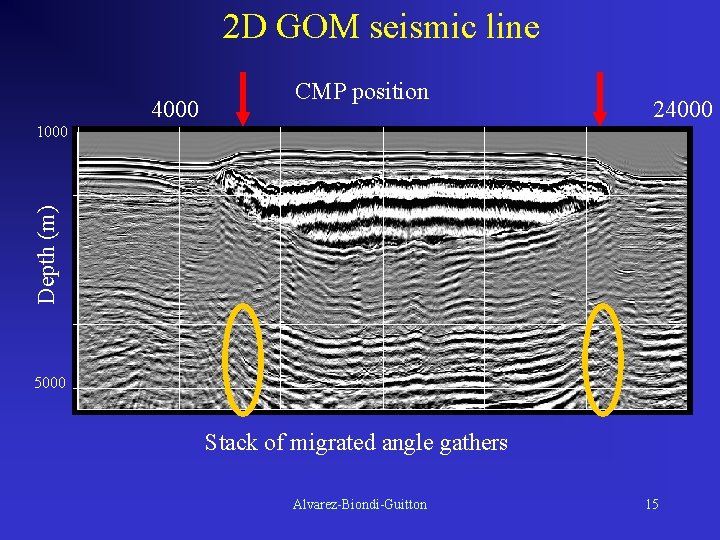
2 D GOM seismic line 4000 CMP position 24000 Depth (m) 1000 5000 Stack of migrated angle gathers Alvarez-Biondi-Guitton 15

Salt-edge ADCIGs Aperture-angle (degrees) 0 60 -60 1000 0 60 Depth (m) -60 1000 Aperture-angle (degrees) 5000 ADCIG 1: Left edge ADCIG 2: Right edge Alvarez-Biondi-Guitton 16

Comparison of Radon Transforms Curvature (m) -400 1000 0 Curvature (m) 2000 -400 1000 0 2000 Depth (m) Primaries 5000 2 D transform γa=0 plane from 3 D transform Alvarez-Biondi-Guitton 17

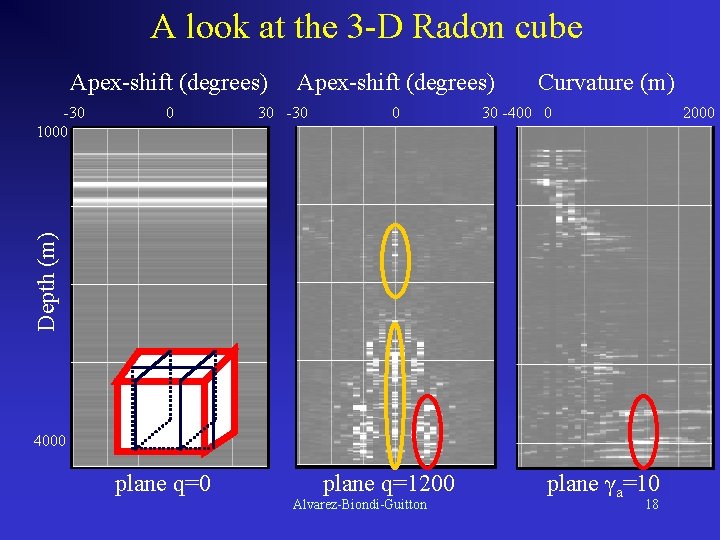
A look at the 3 -D Radon cube Apex-shift (degrees) 0 30 -30 0 Curvature (m) 30 -400 0 2000 Depth (m) -30 1000 Apex-shift (degrees) 4000 plane q=1200 Alvarez-Biondi-Guitton plane γa=10 18

Results of Multiple Attenuation Aperture-angle (degrees) 0 60 -60 1000 0 60 Depth (m) -60 1000 Aperture-angle (degrees) 5000 ADCIG 1: Left edge ADCIG 2: Right edge Alvarez-Biondi-Guitton 19

Primaries ADCIG 1 Aperture-angle (degrees) -40 0 0 40 3200 Depth (m) 3200 40 5200 standard transform apex-shifted transform Alvarez-Biondi-Guitton 20

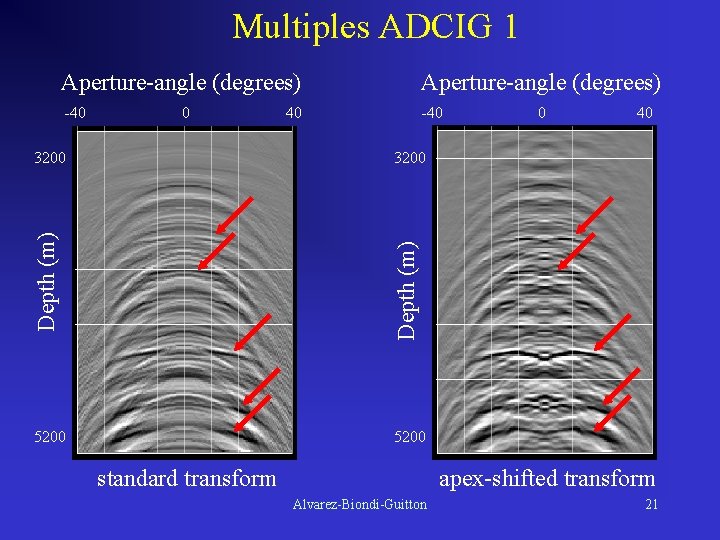
Multiples ADCIG 1 Aperture-angle (degrees) -40 0 0 40 3200 Depth (m) 3200 40 5200 standard transform apex-shifted transform Alvarez-Biondi-Guitton 21

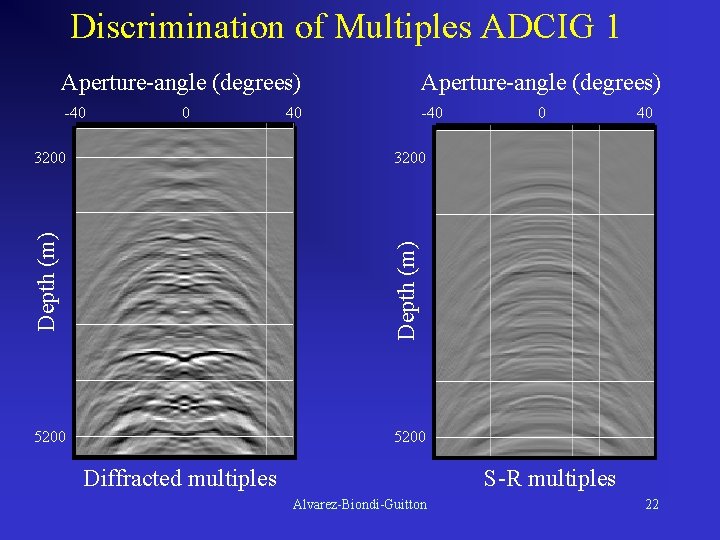
Discrimination of Multiples ADCIG 1 Aperture-angle (degrees) -40 0 0 40 3200 Depth (m) 3200 40 5200 Diffracted multiples S-R multiples Alvarez-Biondi-Guitton 22

Primaries ADCIG 2 Aperture-angle (degrees) -40 0 0 40 3200 Depth (m) 3200 40 5200 Standard transform Apex-shifted transform Alvarez-Biondi-Guitton 23

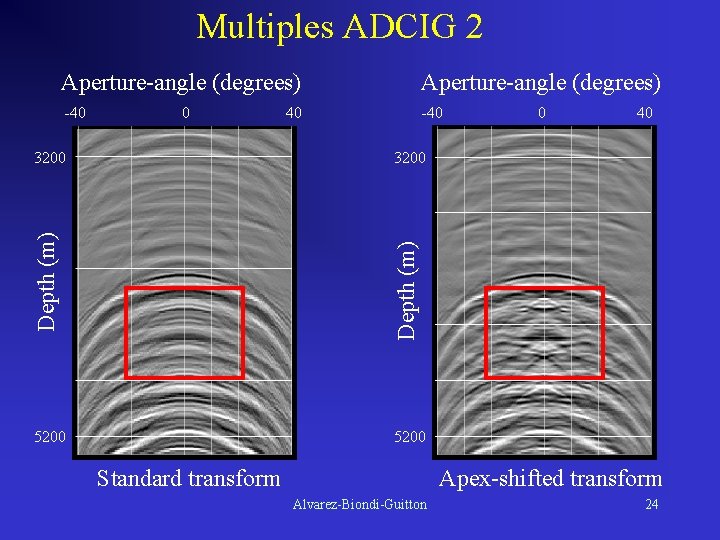
Multiples ADCIG 2 Aperture-angle (degrees) -40 0 0 40 3200 Depth (m) 3200 40 5200 Standard transform Apex-shifted transform Alvarez-Biondi-Guitton 24

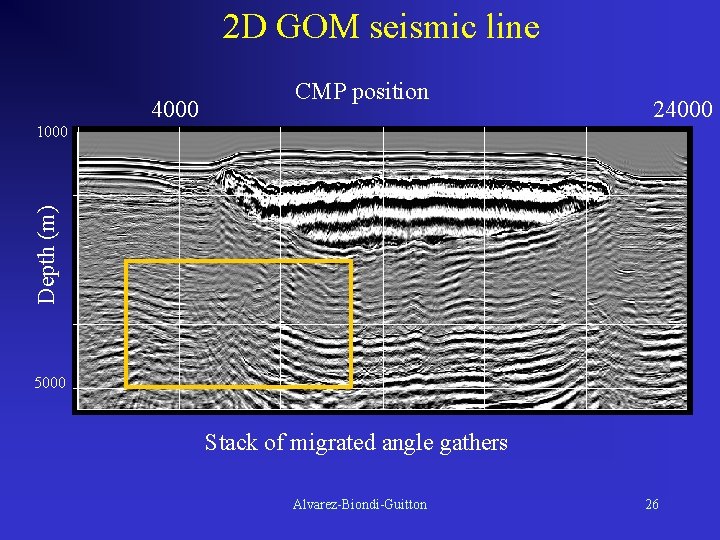
2 D GOM seismic line 4000 CMP position 24000 Depth (m) 1000 5000 Stack of migrated angle gathers Alvarez-Biondi-Guitton 26

Primaries on Angle Stacks Depth (m) 4000 CMP position (m) 10000 3000 2 D-RT 5000 3 D-RT 5000 3000 Diff 5000 Alvarez-Biondi-Guitton 27

Depth (m) Multiples on Angle Stacks 3000 4000 CMP position (m) 10000 2 D-RT 5000 3 D-RT 5000 3000 Diff 5000 Alvarez-Biondi-Guitton 28

Conclusions The apex-shifted Radon transform is an effective way to attenuate diffracted multiples in the image space. The usual trade-off between multiple attenuation and primary preservation remains. Alvarez-Biondi-Guitton 29

Opportunities and challenges In 3 D data, the apex-shift is a function of azimuth as well as aperture angle. We will takeadvantage of the development of 3 D ADCIGs. The challenge is to handle the increased dimensionality of the problem. Alvarez-Biondi-Guitton 30

Thank you for your attention. I will be happy to entertain your questions. Alvarez-Biondi-Guitton 31

Apex-shifted Radon Transform From model space to data space (ADCIGs): From γ: aperture data space angle to model space: q: moveout curvature h: apex-shift distance z, z’: depth γ: aperture angle q: moveout curvature h: apex-shift distance z, z’: depth Alvarez-Biondi-Guitton 33

Constrained LS inversion Apex-shifted Radon transform: Objective Function: Cauchy regularization ε: controls level of sparsity in model space b: controls minimum value below which to zero out model space Alvarez-Biondi-Guitton 34