Atoms the Periodic Table and Ions Dr Stephen

Atoms, the Periodic Table, and Ions Dr. Stephen Crabtree September 5, 2018

Some Basic Chemistry Matter: Any substance which has mass and occupies space. Elements: The unique building blocks of all matter. Atoms: The smallest unit of an element that has the properties of that element Molecules: Groups of bound atoms, the smallest units of a material that have its properties

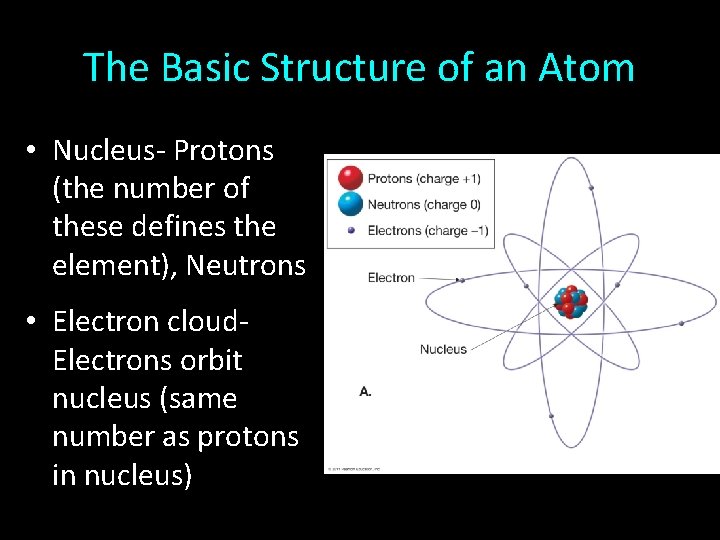
The Basic Structure of an Atom • Nucleus- Protons (the number of these defines the element), Neutrons • Electron cloud. Electrons orbit nucleus (same number as protons in nucleus)

Isotopes • Mass number = sum of neutrons + protons in an atom. • An isotope is an atom that exhibits variation in its mass number. • Unstable isotopes emit particles and energy in a process known as radioactive decay.

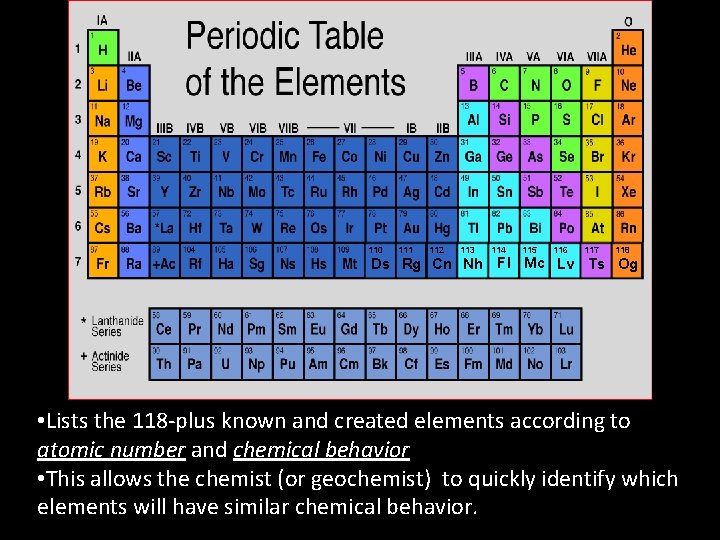
110 111 112 113 114 115 116 117 118 Ds Rg Cn Nh Fl Mc Lv Ts Og • Lists the 118 -plus known and created elements according to atomic number and chemical behavior • This allows the chemist (or geochemist) to quickly identify which elements will have similar chemical behavior.

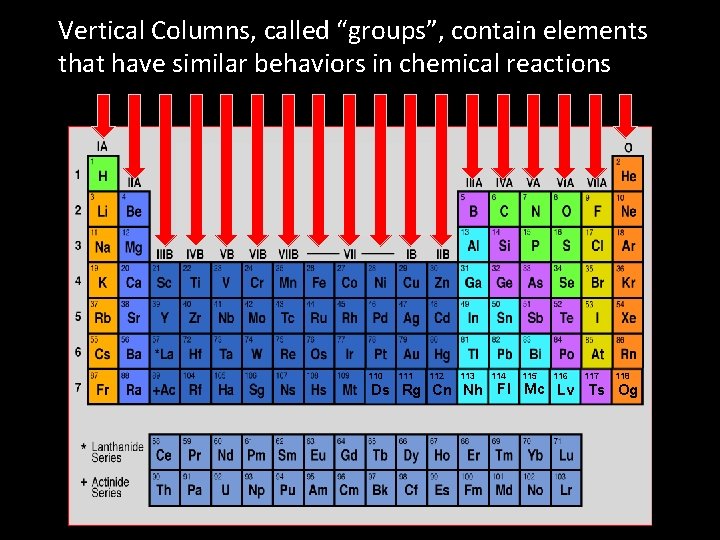
Vertical Columns, called “groups”, contain elements that have similar behaviors in chemical reactions 110 111 112 113 114 115 116 117 118 Ds Rg Cn Nh Fl Mc Lv Ts Og

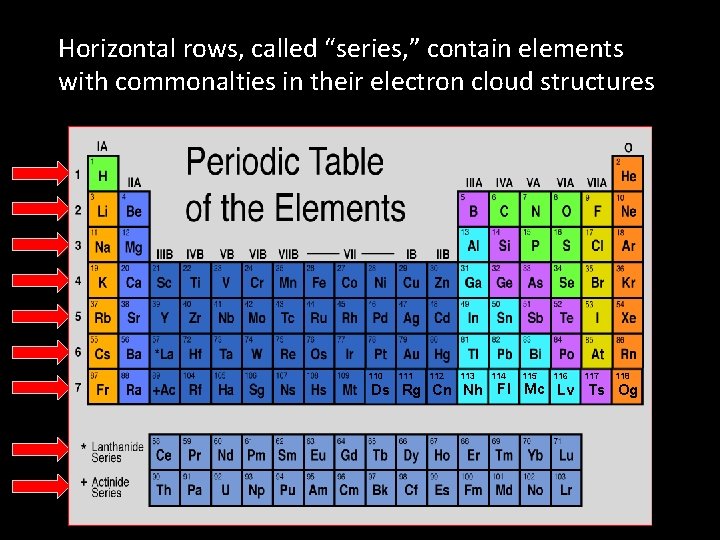
Horizontal rows, called “series, ” contain elements with commonalties in their electron cloud structures 110 111 112 113 114 115 116 117 118 Ds Rg Cn Nh Fl Mc Lv Ts Og

This Image is NOT a Realistic Depiction • Why is it used? – It’s the Bohr model of the atom – Depicts a simplified system of orbits based on energy levels emitted – Easy to comprehend orbits like planets around a sun

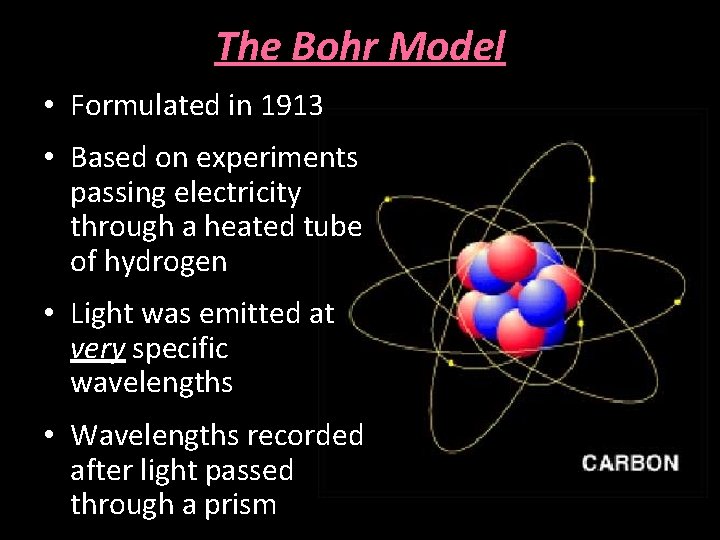
The Bohr Model • Formulated in 1913 • Based on experiments passing electricity through a heated tube of hydrogen • Light was emitted at very specific wavelengths • Wavelengths recorded after light passed through a prism

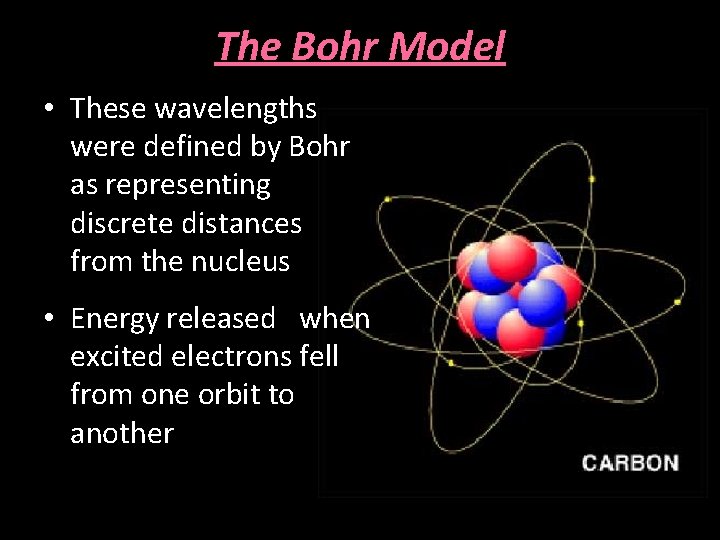
The Bohr Model • These wavelengths were defined by Bohr as representing discrete distances from the nucleus • Energy released when excited electrons fell from one orbit to another

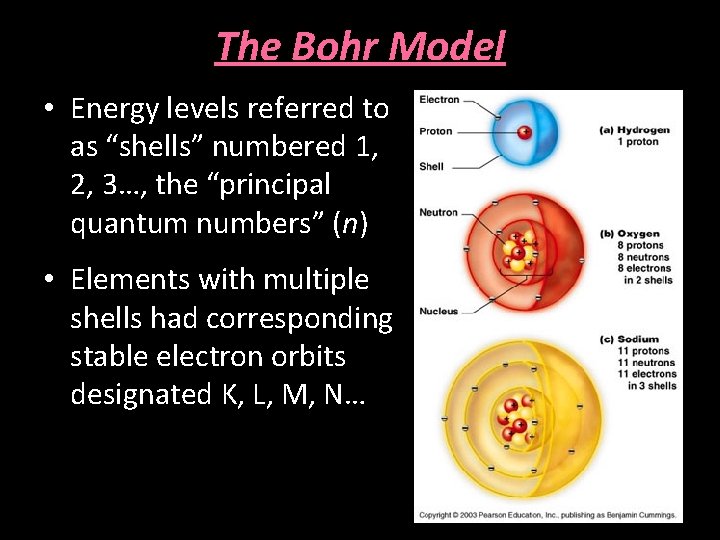
The Bohr Model • Energy levels referred to as “shells” numbered 1, 2, 3…, the “principal quantum numbers” (n) • Elements with multiple shells had corresponding stable electron orbits designated K, L, M, N…

This Image is NOT a Realistic Depiction • Model was unable to explain observations from more complex atoms than hydrogen • Did not allow for elliptical orbits • Did not account for axial spin of electrons • Did not explain energy between levels

The Schrödinger Model • Built on work by de. Broglie (1923) suggesting that electrons behaved like waves • Did away with idea of discrete orbits – Focus on probability of location, not exact location of electrons

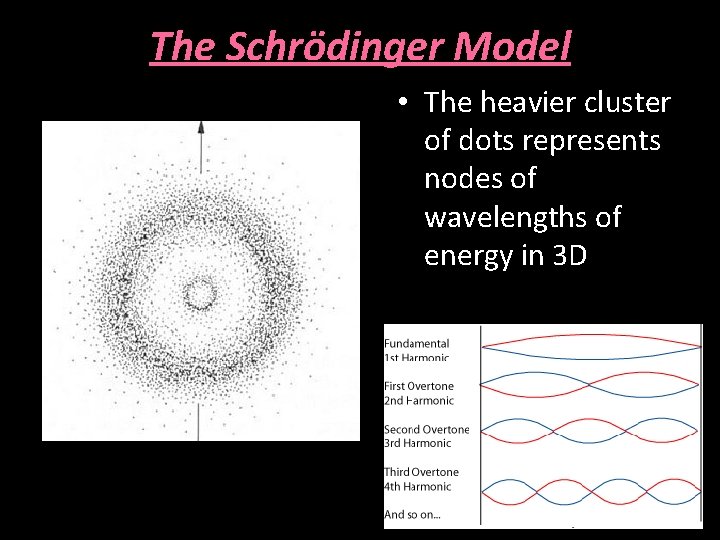
The Schrödinger Model • The heavier cluster of dots represents nodes of wavelengths of energy in 3 D

The Schrödinger Model • Defined “subshells” by “azimuthal quantum numbers” (l) within each shell • Different subshells would have different “orbital” shapes Principal Quantum Number: n = 1 Azimuthal Quantum Number: l = 0 • Can have as many subshell shapes as the principal quantum number (n) for that shell, but calculated based on (n-1)

The Schrödinger Model First orbital, l = 0, spherical shape, abbreviated s Second orbital, l = 1, has a dumbbell shape, abbreviated p Both in 2 nd shell Principal Quantum Number: Azimuthal Quantum Number: n=2 l=0 n=2 l=1

The Schrödinger Model To account for 3 D geometry, included a “magnetic quantum number, ” m for each orbital, defining its orientation m equals the integer range from –l to +l, Principal Quantum Number: Azimuthal Quantum Number: Magnetic Quantum Number: n=2 l=1 m=0 n=2 l=1 m=± 1

The Schrödinger Model Third orbital, l = 2, typically has a paireddumbbell shape, abbreviated d Only starts being filled in 3 rd shell Principal Quantum Number: Azimuthal Quantum Number: n=3 l=2

The Schrödinger Model For third shell (n = 3), and first d orbital (l = 2), m equals the integer range from – 2 to +2 There are five arrangements for the d orbital Principal Quantum Number: Azimuthal Quantum Number: Magnetic Quantum Number: n=3 l=2 m = -2, -1, 0, +1, +2

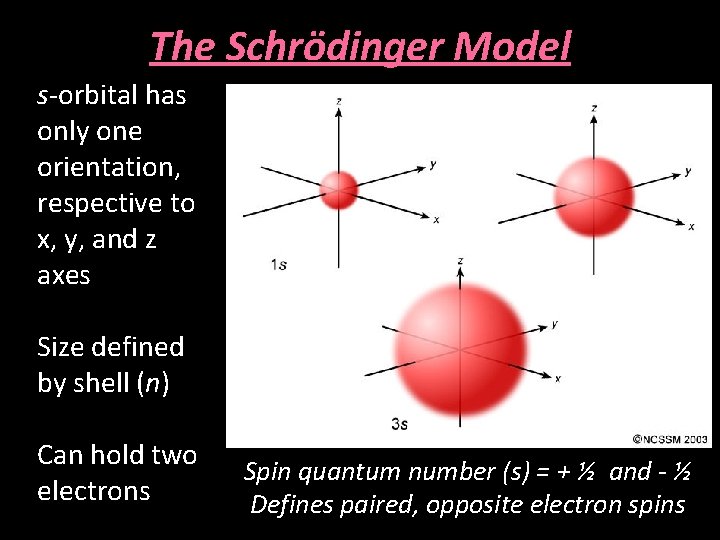
The Schrödinger Model s-orbital has only one orientation, respective to x, y, and z axes Size defined by shell (n) Can hold two electrons Spin quantum number (s) = + ½ and - ½ Defines paired, opposite electron spins

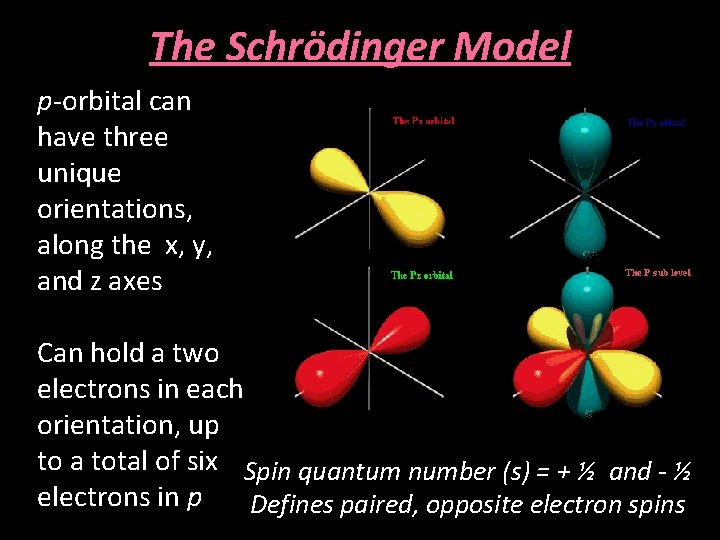
The Schrödinger Model p-orbital can have three unique orientations, along the x, y, and z axes Can hold a two electrons in each orientation, up to a total of six Spin quantum number (s) = + ½ and - ½ electrons in p Defines paired, opposite electron spins

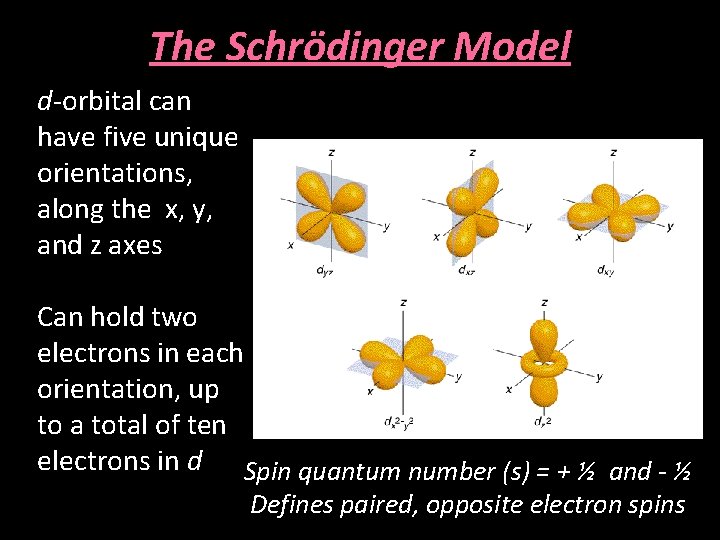
The Schrödinger Model d-orbital can have five unique orientations, along the x, y, and z axes Can hold two electrons in each orientation, up to a total of ten electrons in d Spin quantum number (s) = + ½ and - ½ Defines paired, opposite electron spins

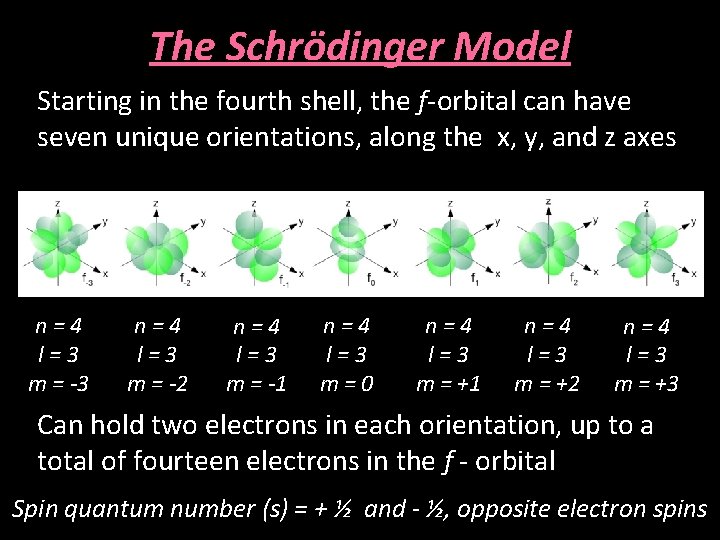
The Schrödinger Model Starting in the fourth shell, the f-orbital can have seven unique orientations, along the x, y, and z axes n=4 l=3 m = -3 n=4 l=3 m = -2 n=4 l=3 m = -1 n=4 l=3 m=0 n=4 l=3 m = +1 n=4 l=3 m = +2 n=4 l=3 m = +3 Can hold two electrons in each orientation, up to a total of fourteen electrons in the f - orbital Spin quantum number (s) = + ½ and - ½, opposite electron spins

Pauli Exclusion Principle • “No two electrons in any one atom may have all four quantum numbers the same” • This is why each orbital can have only two electrons • Electrons sharing an orbital must have opposite spins

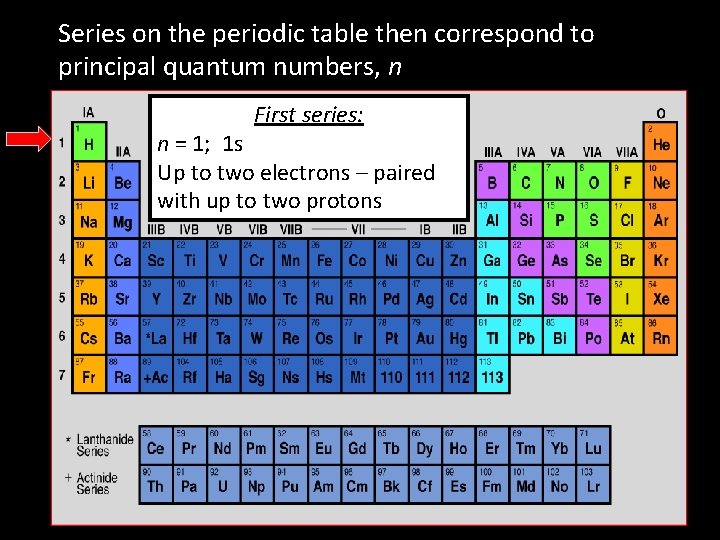
Series on the periodic table then correspond to principal quantum numbers, n First series: n = 1; 1 s Up to two electrons – paired with up to two protons

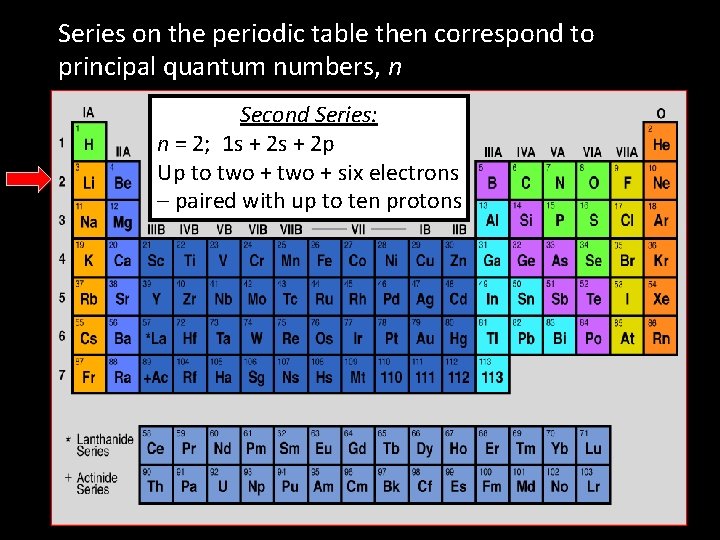
Series on the periodic table then correspond to principal quantum numbers, n Second Series: n = 2; 1 s + 2 p Up to two + six electrons – paired with up to ten protons

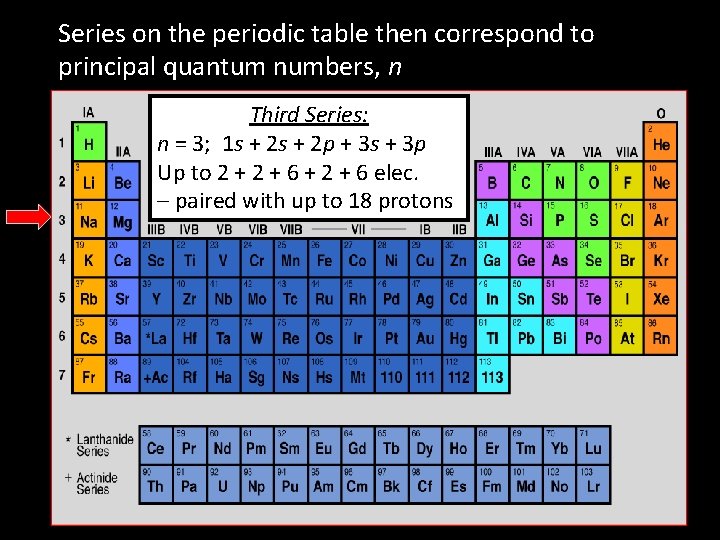
Series on the periodic table then correspond to principal quantum numbers, n Third Series: n = 3; 1 s + 2 p + 3 s + 3 p Up to 2 + 6 + 2 + 6 elec. – paired with up to 18 protons

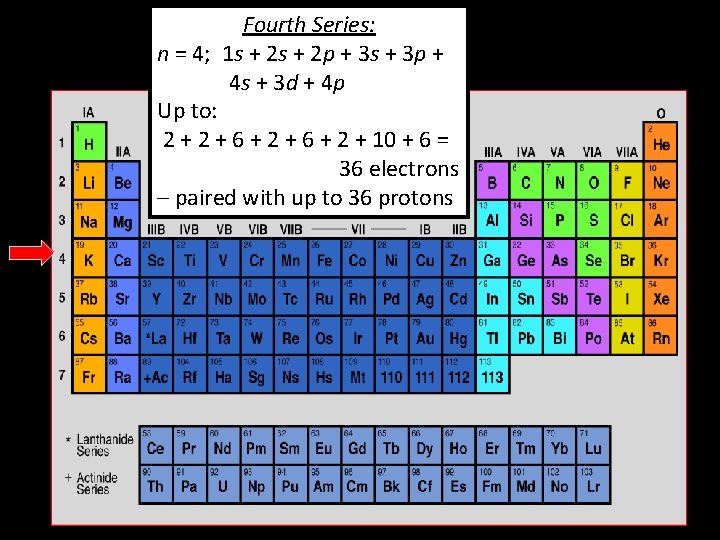
Fourth Series: n = 4; 1 s + 2 p + 3 s + 3 p + 4 s + 3 d + 4 p Up to: 2 + 6 + 2 + 10 + 6 = 36 electrons – paired with up to 36 protons

Example from Periodic Table • To get to a total of eight electrons, to balance eight protons… – 1 s --- 2 electrons – 2 p --- 4 electrons (up to 6 available) Electrons in 2 p will be distributed between the subshells: 2 px , 2 py , or 2 pz 8 O Oxygen

Example from Periodic Table • To get to a total of 33 electrons, to balance 33 protons… – 1 s --- 2 electrons – 2 s --- 2 electrons 33 – 2 p --- 6 electrons – 3 s --- 2 electrons – 3 p --- 6 electrons – 4 s --- 2 electrons – 3 d --- 10 electrons – 4 p --- 3 electrons (up to 6 available) As Arsenic Electrons in 2 p will fill ½ of each subshell: 4 px , 4 py , or 4 pz

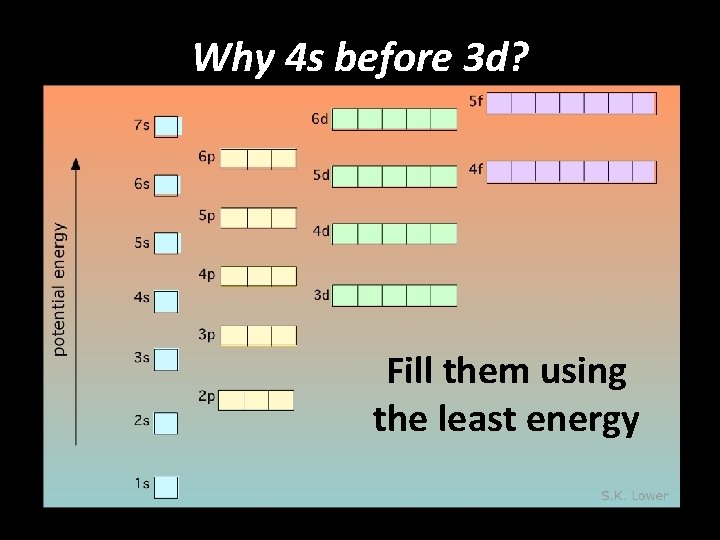
Why 4 s before 3 d? Fill them using the least energy

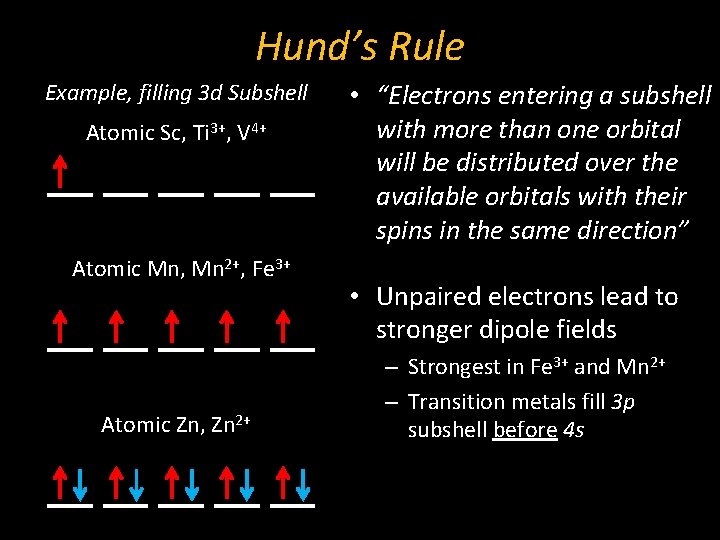
Hund’s Rule Example, filling 3 d Subshell Atomic Sc, Ti 3+, V 4+ Atomic Mn, Mn 2+, Fe 3+ Atomic Zn, Zn 2+ • “Electrons entering a subshell with more than one orbital will be distributed over the available orbitals with their spins in the same direction” • Unpaired electrons lead to stronger dipole fields – Strongest in Fe 3+ and Mn 2+ – Transition metals fill 3 p subshell before 4 s

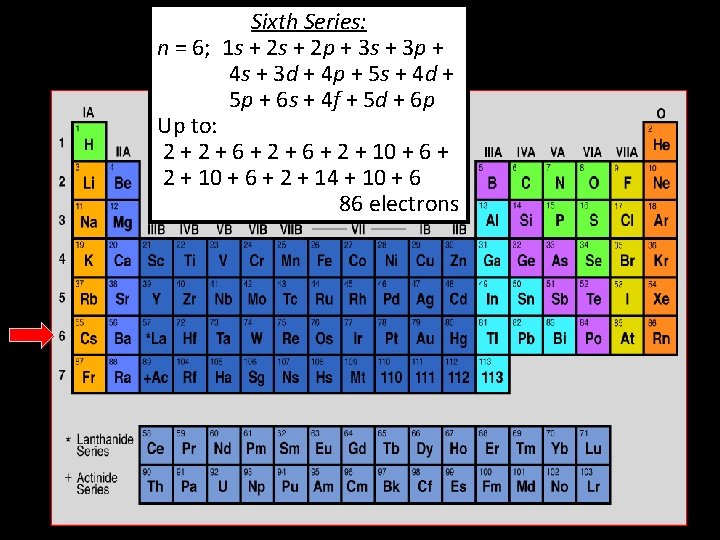
Sixth Series: n = 6; 1 s + 2 p + 3 s + 3 p + 4 s + 3 d + 4 p + 5 s + 4 d + 5 p + 6 s + 4 f + 5 d + 6 p Up to: 2 + 6 + 2 + 10 + 6 + 2 + 14 + 10 + 6 86 electrons

Shorthand Notation using Noble Gases He 1 s 2 Helium Ne Argon Xe [Kr] 5 s 2 4 d 10 5 p 6 Rn [Xe] 6 s 2 5 d 10 4 f 14 6 p 6 Krypton 1 s 2 2 p 6 Neon Ar Kr [Ar] 4 s 2 3 d 10 4 p 6 Xenon [Ne] 3 s 2 3 p 6 Radon

Example from Periodic Table • To get to a total of 79 electrons, to balance 79 protons… – [Kr] --- 36 electrons – 5 s --- 2 electrons – 4 d --- 10 electrons – 5 p --- 6 electrons – 6 s --- 2 electrons – 4 f --- 14 electrons – 5 d --- 9 electrons (up to 10 available) Au 79 Gold Could also use shorthand: [Xe] 6 s 2 4 f 14 5 d 9

• Ions Why does all this matter? – All atoms want their outermost shells filled – Ions are formed when atoms gain or lose electrons cation anion

Noble gases do not lose or gain. They are already filled

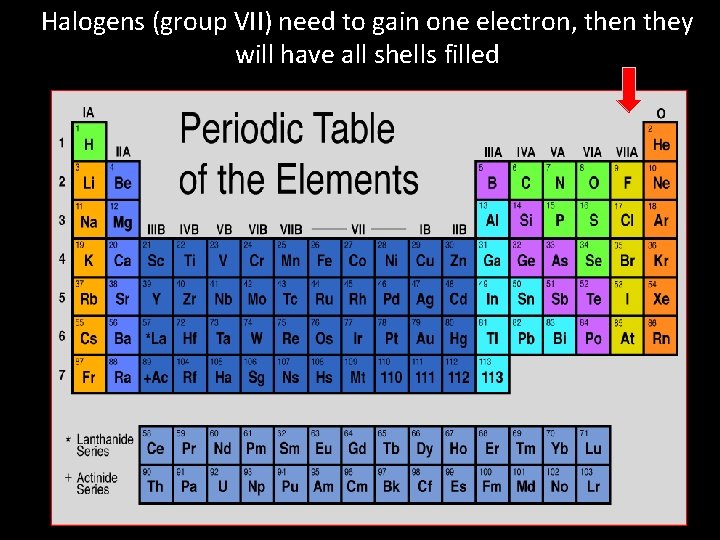
Halogens (group VII) need to gain one electron, then they will have all shells filled

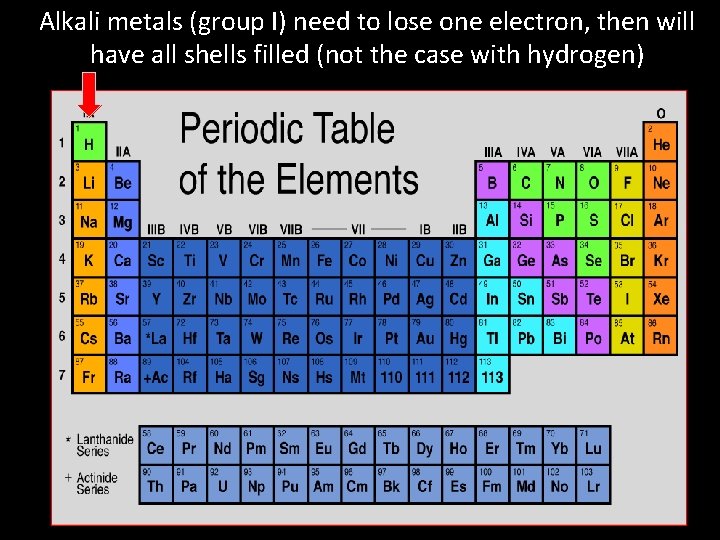
Alkali metals (group I) need to lose one electron, then will have all shells filled (not the case with hydrogen)

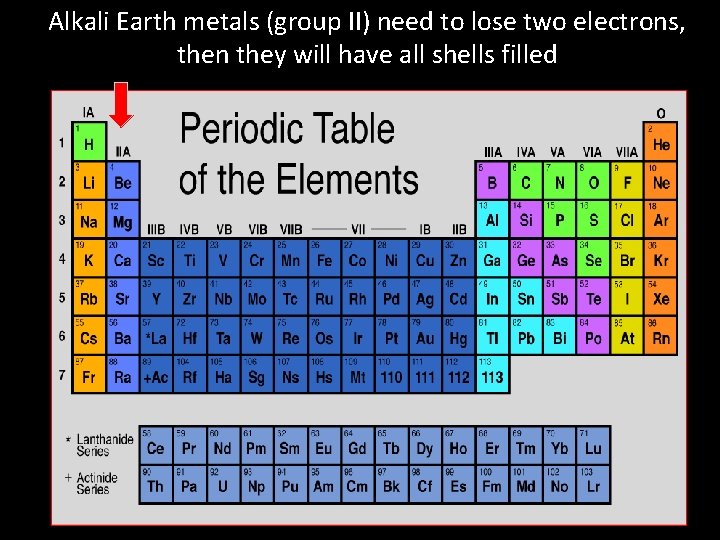
Alkali Earth metals (group II) need to lose two electrons, then they will have all shells filled

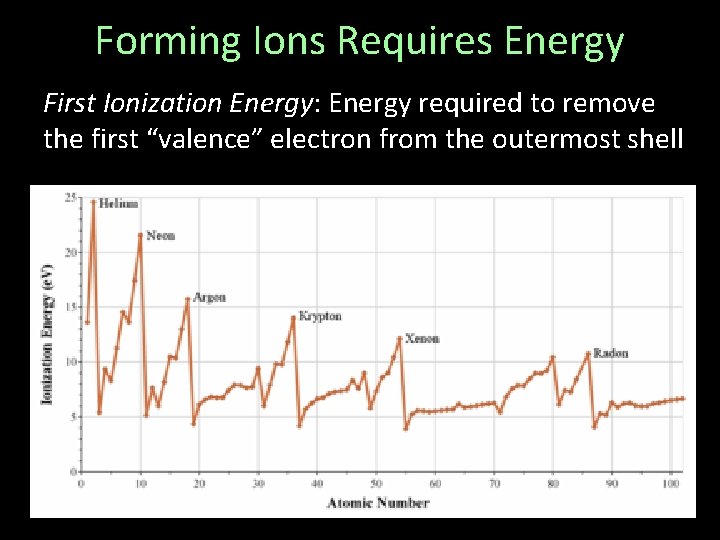
Forming Ions Requires Energy First Ionization Energy: Energy required to remove the first “valence” electron from the outermost shell

Forming Ions Requires Energy Far easier to remove the outermost electrons from group I, or II than groups VI and VII When the shell is already nearly empty, it is easier to empty

Forming Ions Requires Energy Also quite easy to remove outermost “valence” electron from group IIIA (Al, Ga, In, Tl), from nearlyempty p-orbital Some metals, such as iron (Fe), have multiple valence states (ex: Fe 2+ and Fe 3+)

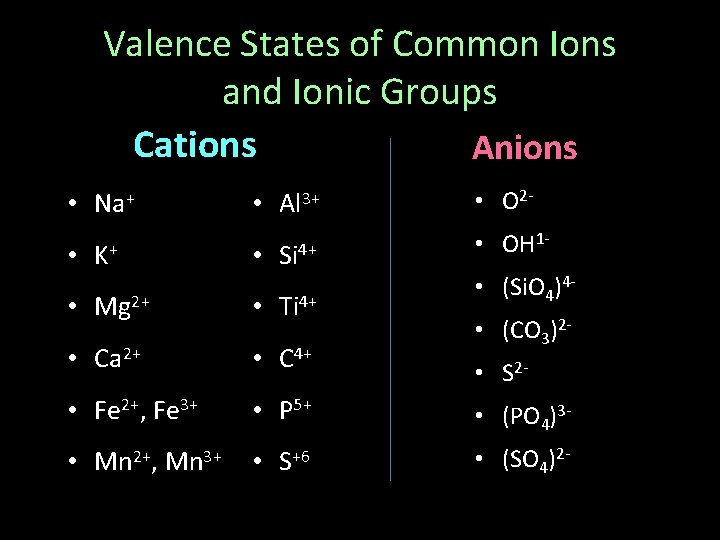
Valence States of Common Ions and Ionic Groups Cations Anions • Na+ • K+ • Al 3+ • Si 4+ • O 2 • OH 1 • (Si. O 4)4 - • Mg 2+ • Ti 4+ • Ca 2+ • C 4+ • Fe 2+, Fe 3+ • P 5+ • (PO 4)3 - • Mn 2+, Mn 3+ • S+6 • (SO 4)2 - • (CO 3)2 • S 2 -

Electronegativity Atoms with high electronegativity are more likely to gain electrons than to lose them

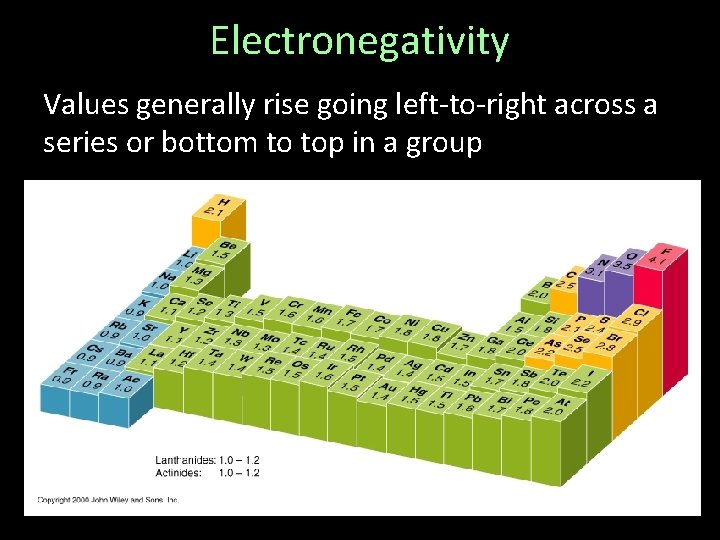
Electronegativity Values generally rise going left-to-right across a series or bottom to top in a group

Electronegativity Two elements with very different electronegativity values are likely to bond strongly to each other + =

Summary: Basic Terms Matter: Any substance that has mass and occupies space. Elements: The basic building blocks of all matter. Atoms: The smallest unit of an element that has the properties of that element Molecules: Groups of bound atoms, the smallest units of a material that have its properties Protons (+) and Neutrons (0) in the nucleus Electrons (-) orbiting around the nucleus

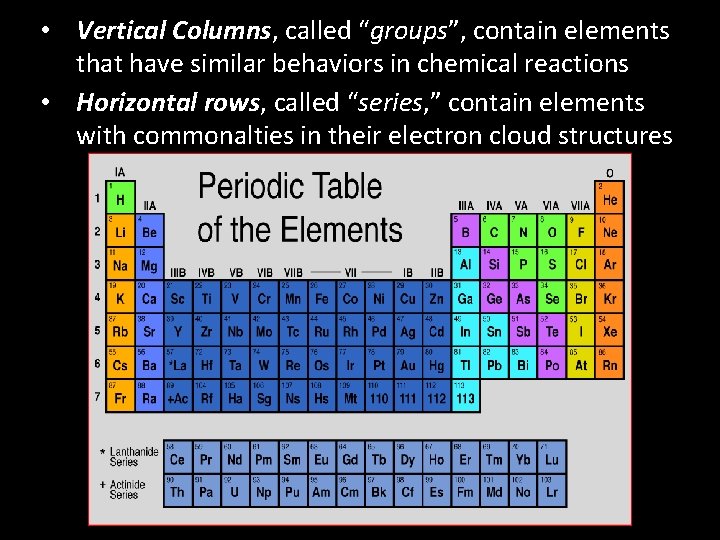
• Vertical Columns, called “groups”, contain elements that have similar behaviors in chemical reactions • Horizontal rows, called “series, ” contain elements with commonalties in their electron cloud structures

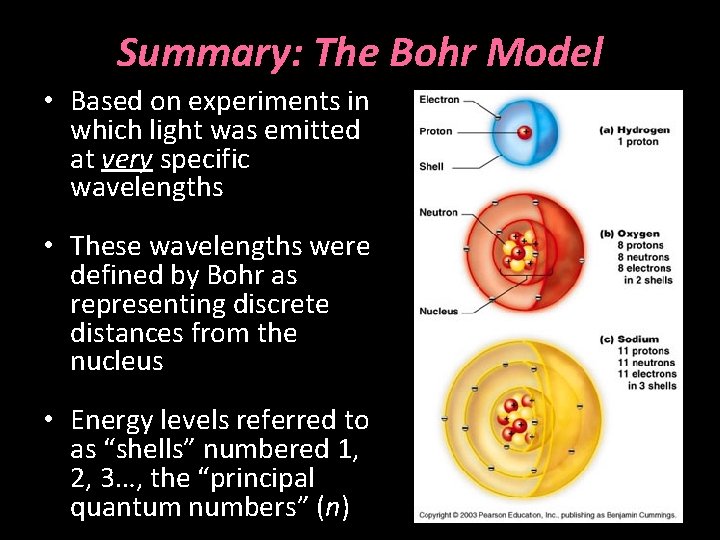
Summary: The Bohr Model • Based on experiments in which light was emitted at very specific wavelengths • These wavelengths were defined by Bohr as representing discrete distances from the nucleus • Energy levels referred to as “shells” numbered 1, 2, 3…, the “principal quantum numbers” (n)

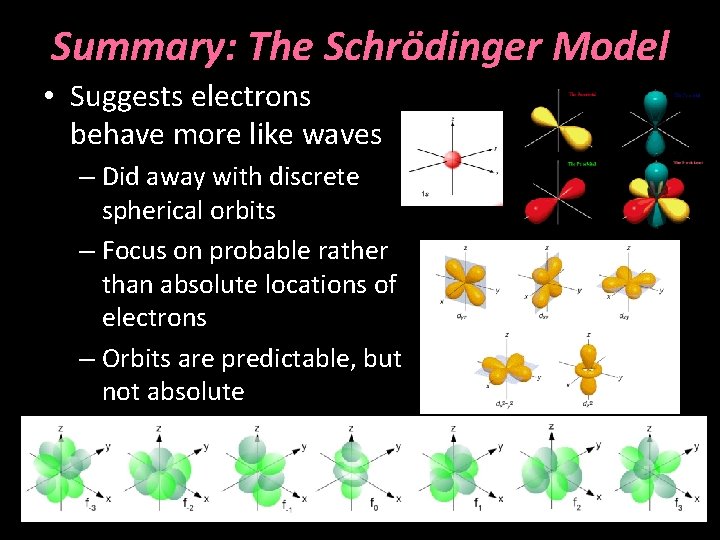
Summary: The Schrödinger Model • Suggests electrons behave more like waves – Did away with discrete spherical orbits – Focus on probable rather than absolute locations of electrons – Orbits are predictable, but not absolute

Summary: Quantum Numbers Principal Quantum Number (n): • Electron shells defined by orbit size, • Equal to periodic table series Azimuthal Quantum Number (l): • Electron subshells, • Defined by shape (s = 0, p = 1, d = 2, f = 3) Magnetic Quantum Number (m): • Electron subshell orientations • Possible orientations allow range from +(l) to –(l) Spin Quantum Number (s): • Each electron equal to either +½ or -½

Summary: Quantum Numbers • Pauli Exclusion Principle – “No two electrons in any one atom may have all four quantum numbers the same” – This is why each orbital can have only two electrons – Electrons sharing an orbital must have opposite spins

Example from Periodic Table • To get to a total of 33 electrons, to balance 33 protons… – 1 s --- 2 electrons – 2 s --- 2 electrons 33 – 2 p --- 6 electrons – 3 s --- 2 electrons – 3 p --- 6 electrons – 4 s --- 2 electrons – 3 d --- 10 electrons – 4 p --- 3 electrons (up to 6 available) As Arsenic Electrons in 2 p will fill 1 ½ of the subshells: 4 px , 4 py , or 4 pz

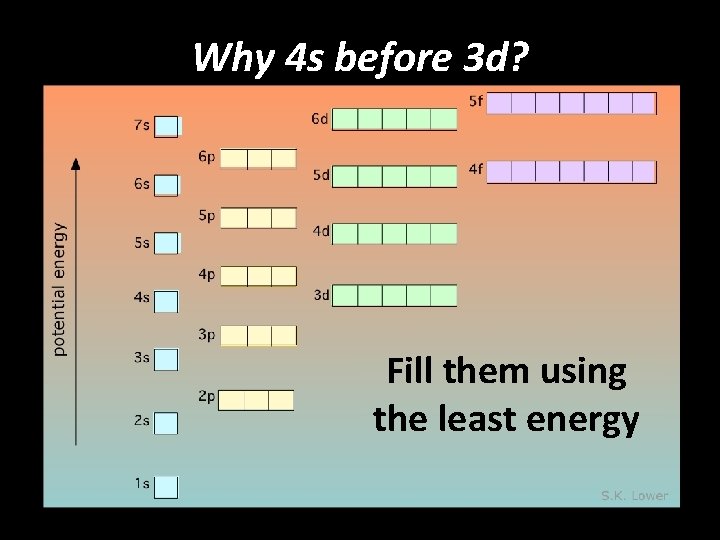
Why 4 s before 3 d? Fill them using the least energy

Summary: Quantum Numbers Example, filling 3 d Subshell Atomic Sc, Ti 3+, V 4+ Atomic Mn, Mn 2+, Fe 3+ Atomic Zn, Zn 2+ • Hund’s Rule – “Electrons entering a subshell with more than one orbital will be distributed over the available orbitals with their spins in the same direction” – Unpaired electrons lead to stronger dipole fields • Strongest in Fe 3+ and Mn 2+ • Transition metals fill 3 p subshell before 4 s

• Ions Summary: Ions – All atoms want their outermost shells filled – Ions are formed when atoms gain or lose electrons cation anion

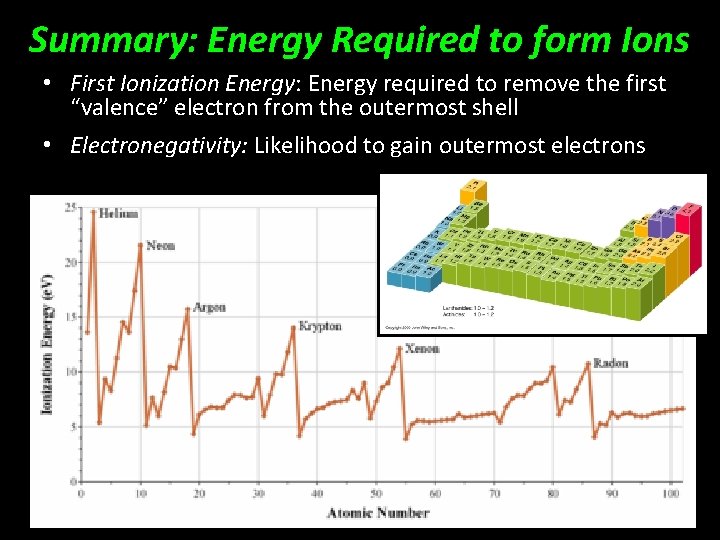
Summary: Energy Required to form Ions • First Ionization Energy: Energy required to remove the first “valence” electron from the outermost shell • Electronegativity: Likelihood to gain outermost electrons

Next Time… • Chemical Bonds – From atoms to molecules • Ionic radii – What determines whether atoms fit into crystals