Atomic Theory Notes Waves What is a wave

Atomic Theory Notes

Waves What is a wave? https: //www. youtube. com/watch? v=Iuv 6 h. Y 6 zsd 0 Wave – Disturbance in a field which transfers energy

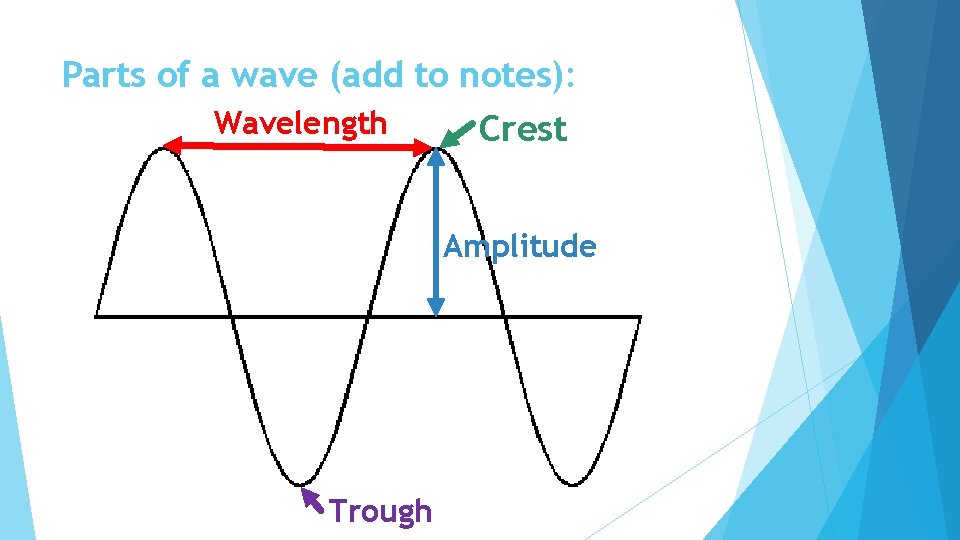
Parts of a wave (add to notes): Wavelength Crest Amplitude Trough

Waves http: //phet. colorado. edu/en/simulation/wave-on-a-string Why we believe light moves in waves.

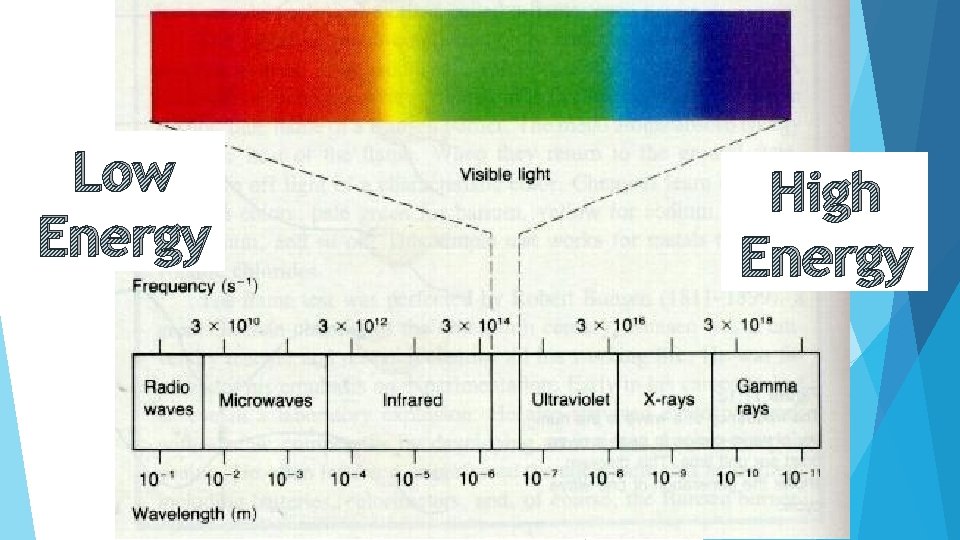
Waves Frequency - # of waves to go by in 1 second Units are in Hz or Hertz Electromagnetic Spectrum – Disturbance in electric and magnetic field

Waves https: //www. youtube. com/watch? v=YYNyne. Nqm 0 c The speed of a wave: Speed m/s The C = Wave length x frequency m Hz speed of light: =λx. F Speed of light = 3 x 108 meters/second 300, 000 meters/second

Putting the speed of a wave into perspective 300, 000 m/s = 670, 000 mph = 186, 000 miles per second 25, 000 miles = circumference of the Earth In It 1 second light will travel around the Earth 7. 5 times! is 480, 000 miles round trip to the moon It takes light 2. 6 seconds to go from here to the moon and back (this has been tested with lasers, we shot a laser beam at a mirror on the moon and timed how long it took the light to get back to us on Earth)

Example Problems Sound waves in air travel at approximately 330 m/s. Calculate the frequency of a 2. 5 m-long sound wave. A wave on a certain guitar string travels at a speed of 200 m/s. Calculate the wavelength of an “A” note sounding at 440 Hz.

Example Problems Find the wavelength of a wave traveling at 20 m/s at a frequency of 5 Hz. Find the speed of a wave with a frequency of 8 Hz and a wavelength of 16 m.

Light and Colors All light has the same speed. How do we get different colors? Light waves moving at different frequencies and having different wavelengths. What colors can we get? Red, Orange, Yellow, Green, Blue, Indigo, Violet Which has the smallest wavelength and which has the largest wavelength? Smallest Largest - Violet - Red

Lab Discussion What color had the most energy? Blue in lab. Overall Violet. What kind of relationship is there between wavelength and energy? Inverse relationship between wavelength and energy As wavelength increases energy decreases As wavelength decreases energy increases

Energy is like a ladder the higher you go the more energy you have. Why do you have more energy when you are higher up on the ladder? You have farther to fall. Atoms work the same way the farther from the nucleus electrons go the more energy they have because it has a farther distance it can travel. When electrons are at their lowest energy orbital possible we call it the ground state.

Out of the following list order the colors from most amount of energy down to the least: ______ Purple Light (400 nm) ______ Blue light (440 nm) ______ Red light (680 nm) ______ Teal light (520 nm) If we were putting them on the above target identify which number goes with which color

Spectrum Order the following from least amount of energy to most amount of energy: Visible light, radio waves, x-rays, UV rays, infrared light, gamma rays and microwaves

Low Energy High Energy

Electromagnetic Spectrum https: //www. youtube. com/watch? v=kf. S 5 Qn 0 wn 2 o https: //www. youtube. com/watch? v=lwf. JPc-r. SXw

Planck Every wavelength has a certain amount of energy associated with it. Because of this we know light is not a continuous wave but instead a particle or photon. Light is photons or quanta (small packets of energy/waves).

Planck’s Equation E =hx. F h = 6. 63 x 10 -34 Js Use if only frequency is given to you E = h x (c/λ) Use if you know 2 of the following: Speed Wavelength We already know: C = λ x f Energy

Example Problems A photon has a frequency of 2. 68 x 106 Hz. Calculate its energy. A photon of light has a wavelength of 0. 050 cm. Calculate its energy.