Atomic Structure and Periodicity CHAPTER 7 Objectives Explain

Atomic Structure and Periodicity CHAPTER 7

Objectives Explain properties of light Explain the nature of matter Explain the photoelectric effect Calculate light energy, frequency, and wavelengths of
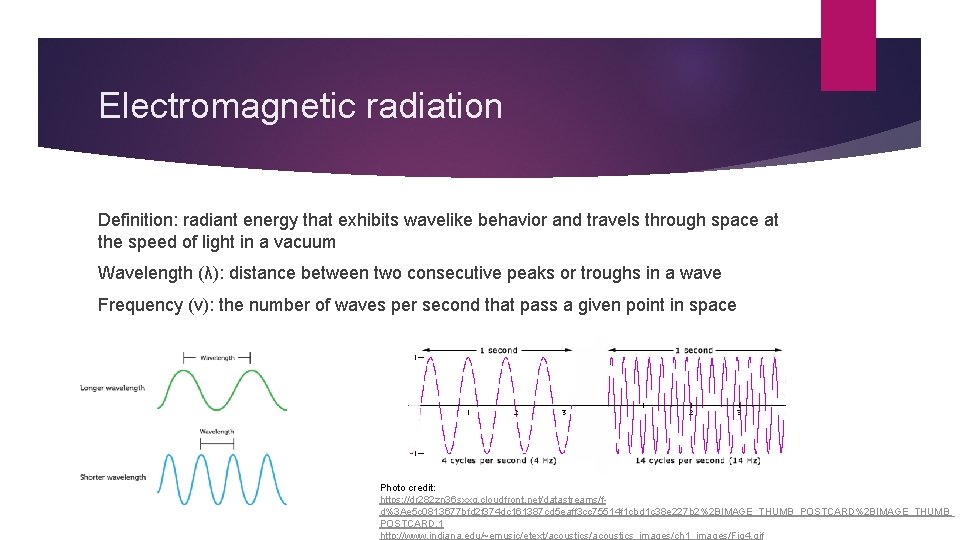
Electromagnetic radiation Definition: radiant energy that exhibits wavelike behavior and travels through space at the speed of light in a vacuum Wavelength (λ): distance between two consecutive peaks or troughs in a wave Frequency (ν): the number of waves per second that pass a given point in space Photo credit: https: //dr 282 zn 36 sxxg. cloudfront. net/datastreams/fd%3 Ae 5 c 0813677 bfd 2 f 374 dc 161387 cd 5 eaff 3 cc 75514 f 1 cbd 1 c 38 e 227 b 2%2 BIMAGE_THUMB_POSTCARD%2 BIMAGE_THUMB_ POSTCARD. 1 http: //www. indiana. edu/~emusic/etext/acoustics_images/ch 1_images/Fig 4. gif
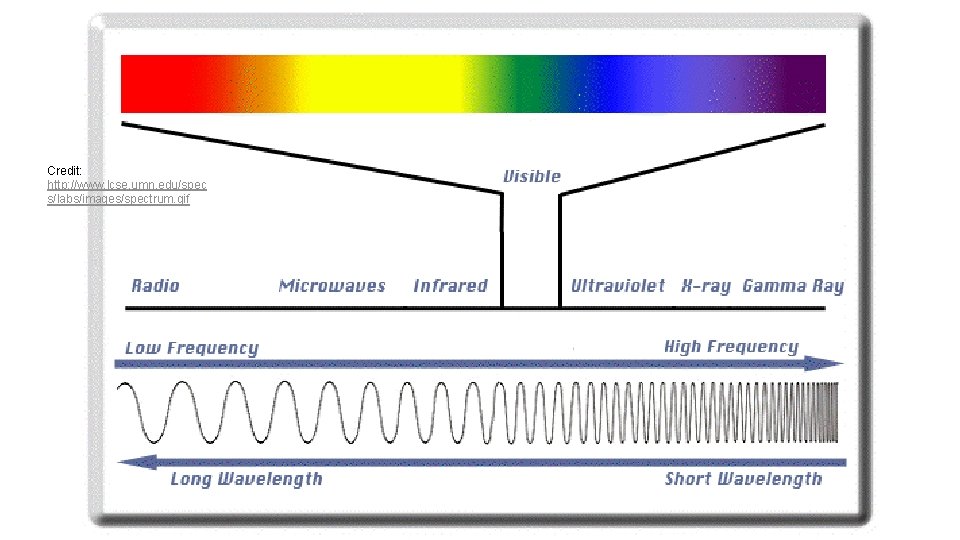
Credit: http: //www. lcse. umn. edu/spec s/labs/images/spectrum. gif

Relationship of λ and ν Speed of light 3. 00 x 108 m/s = (wavelength in meters)(frequency in Hz) Longer wavelengths = lower frequency = low pitch Shorter wavelengths = higher frequency = high pitch Example 7. 1 (p. 298) Λ = 650 nm c = 3. 00 x 108 m/s Convert 650 nm m Equation: c = λν

#39 p. 342 Q: The laser in an audio CD player uses light with a wavelength of 7. 80 x 102 nm. Calculate the frequency of this light. A: λ = 780 nm c = 3. 00 x 108 m/s Convert to m and solve using c = λν

#40 p. 342 Q: An FM radio station broadcasts at 99. 5 MHz. Calculate the wavelength of the corresponding radio waves. A: v = 99. 5 MHz Convert MHz Hz Solve using c = λν c = 3. 00 x 108 m/s

End of the 19 th century Matter was made of particles Energy (in the form of light) is described as a wave Particles had mass and their position in space could be specified Waves had no mass and their position could not be determined Matter and light did not interact with each other

Max Planck (1858 -1947) Studying radiation profiles Could not explain the behavior of the matter using the known physics Postulated that energy can be gained/lost in whole number multiples of the quantity hv h = Plancks constant = 6. 626 x 10 -34 J ˑ s E = nhv n = integer h = Plancks constant v = frequency of the radiation Energy could be quantized as small packets (quanta)

Albert Einstein Electromagnetic radiation is a stream of particles (photons) Described the energy of the photon using Plancks constant E = hc/v E is energy h is Plancks constant C is the speed of light v is the frequency of the radiation

Example 7. 2 p. 299 The blue color in fireworks is often achieved by heating copper(I) chloride to about 1200˚ C. Then the compound emits blue light having a wavelength of 450 nm. What is the increment of energy (the quantum) that is emitted at 4. 50 x 102 nm by Cu. Cl? Equation: E = hv h = 6. 626 x 10 -34 Jˑs λ = 450 nm (convert to m) c = 3. 00 x 108 m/s c = λv

#41 p. 342 Microwave radiation has a wavelength on the order of 1. 0 cm. Calculate the frequency and the energy of a single photon of this radiation. Equation: h = 6. 626 x 10 -34 Jˑs c = 3. 00 x 108 m/s λ = 1. 0 cm (convert to m) E = hv c = λv

#42 p. 342 A photon of ultraviolet (UV) light possesses enough energy to mutate a strand of human DNA. What is the energy of a single UV photon having a wavelength of 25 nm? Equation: h = 6. 626 x 10 -34 Jˑs c = 3. 00 x 108 m/s λ = 25 nm (convert to m) E = hv c = λv
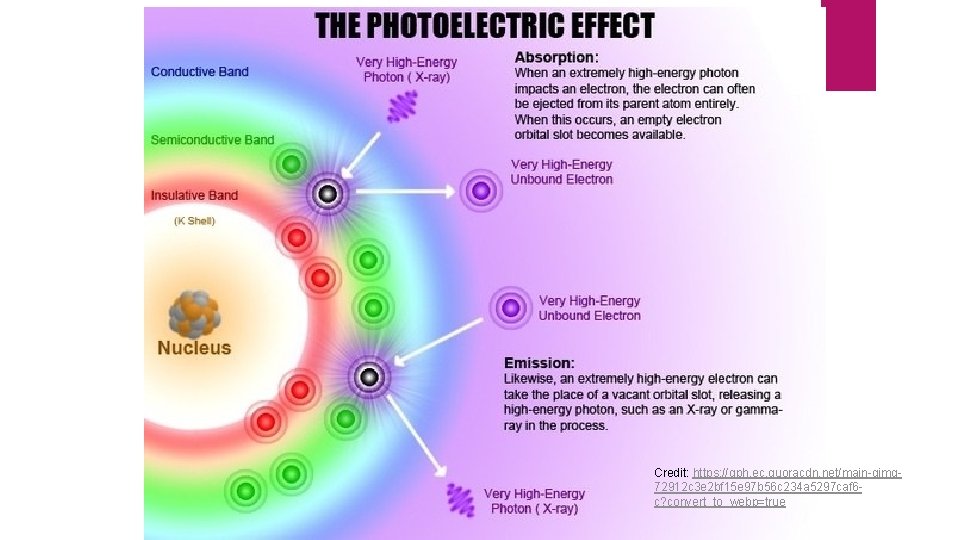
Credit: https: //qph. ec. quoracdn. net/main-qimg 72912 c 3 e 2 bf 15 e 97 b 56 c 234 a 5297 caf 6 c? convert_to_webp=true
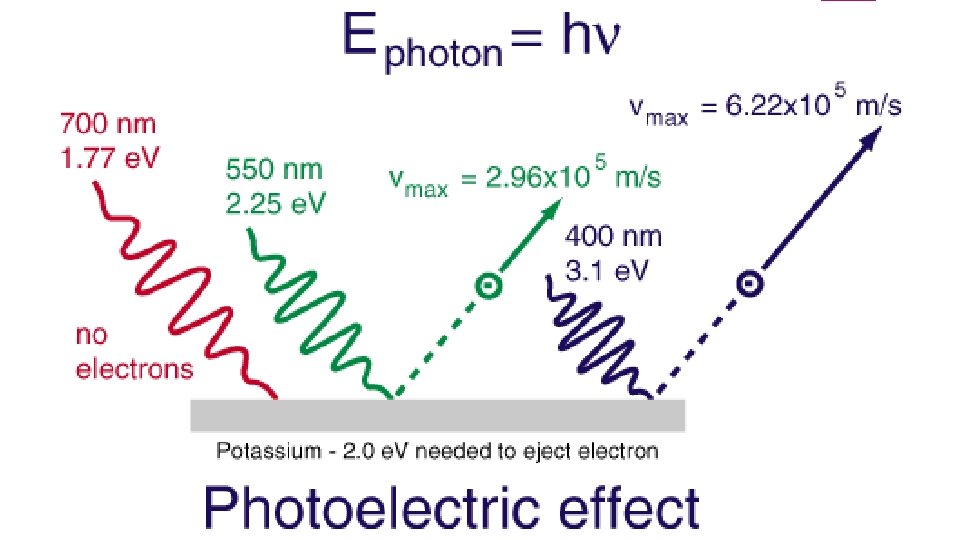

Photoelectric Effect No electrons are emitted by a given metal below a specified threshold frequency, v 0 For light with frequency lower than v 0, no electrons are emitted regardless of light intensity For light with frequency greater than v 0, the number of electrons emitted increases with increasing intensity For light with frequency greater than v 0, the kinetic energy of the electrons increases linearly with the frequency of light

Energy of a Photon E = mc 2 (in Einstein’s theory, energy has mass) You can calculate the apparent mass of a photon m = E/c 2 If we know the wavelength, we can calculate the energy Ephoton = hc/λ Substitutae Ephoton for E in Einsteins equations and c = 3. 00 x 108 m/s E = energy mphoton = hc/λ/c 2 = h/λc

Example 7. 3 p. 303 Q: Compare the wavelength for an electron (mass = 9. 11 x 10 -31 kg) traveling at a speed of 1. 0 x 107 m/s with that for a ball (mass = 0. 10 kg) traveling at 35 m/s. Given: melectron = 9. 11 x 10 -31 kg Given: velectron = 1. 0 x 107 m/s Constant: h = 6. 626 x 10 -34 Jˑs (or unit kgˑm 2/s Equation: m = h/λv mball = 0. 10 kg vball = 35 m/s

#53 b p. 343 Calculate the de Broglie wavelength for a tennis ball (55 g) served at 35 m/s. Given: Constant: h = 6. 626 x 10 -34 kgˑm 2/s Equation: m = h/λv m = 55 g 0. 055 kg v = 35 m/s

#54 b p. 343 Calculate the velocity of a neutron with a wavelength of 75 pm (1 pm = 10 -12 m). Given: λ = 75 pm 7. 5 x 10 -11 m Constant: h = 6. 626 x 10 -34 kgˑm 2/s Need: massneutron Equation: m = h/λv

#55 p. 343 A particle has a velocity that is 90. % the speed of light. If the wavelength of the particle is 1. 5 x 10 -15 m, calculate the mass of the particle. Given: v = (3. 00 x 108 m/s)(0. 90)λ = 1. 5 x 10 -15 m Constant: h = 6. 626 x 10 -34 kgˑm 2/s Equation: m = h/λv

Behavior of Light Credits: http: //moodle 2. rockyview. ab. ca/pluginfile. php/72896/mod_book/chapter/31855/physics _30/images/m 5/p 30_m 5_083_l. jpg http: //www. ducksters. com/science/physics/wave_reflection. gif https: //www. mat. ucsb. edu/~g. legrady/academic/courses/10 f 200 a/md/image/negative_r efraction. jpg Diffraction: when light is scattered from a regular array of points or lines Reflection: change in direction of a wave when it hits a surface Refraction: the change in direction of a wave when it passes through a different medium

Dual Nature of Light It sometimes acts like a wave: Reflection, refraction, diffraction Frequency, wavelength It sometimes acts like a particle: Energy, mass Electrons are the key: showed particle and wavelike behavior MATTER AND ENERGY ARE NOT DISTINCT All matter exhibits both particulate and wave properties The more mass, acts more like a particle Less mass, shows wave functions more easily
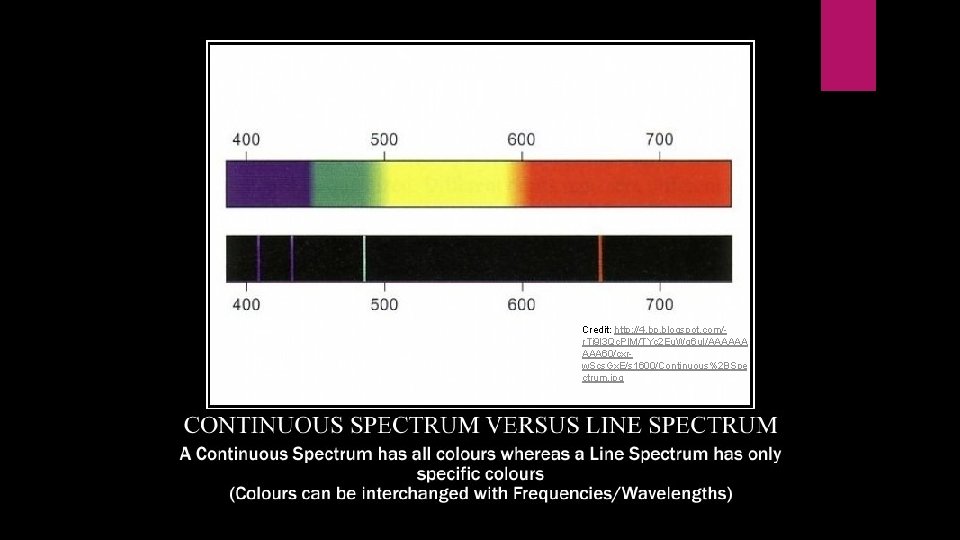
Credit: http: //4. bp. blogspot. com/r. Ti 9 l 3 Qc. PIM/TYc 2 Eu. Wg 6 u. I/AAAAAA 60/cxrw. Scs. Gx. E/s 1600/Continuous%2 BSpe ctrum. jpg

Line Emission Spectrums Continuous: results from white light being passed through a prism. Contains all wavelengths of visible light Line: created from running electricity through an elemental gas (i. e. hydrogen) and observing the spectra Only a few lines of specific wavelengths show up Unique to each element Wavelengths represent energy levels of the electrons
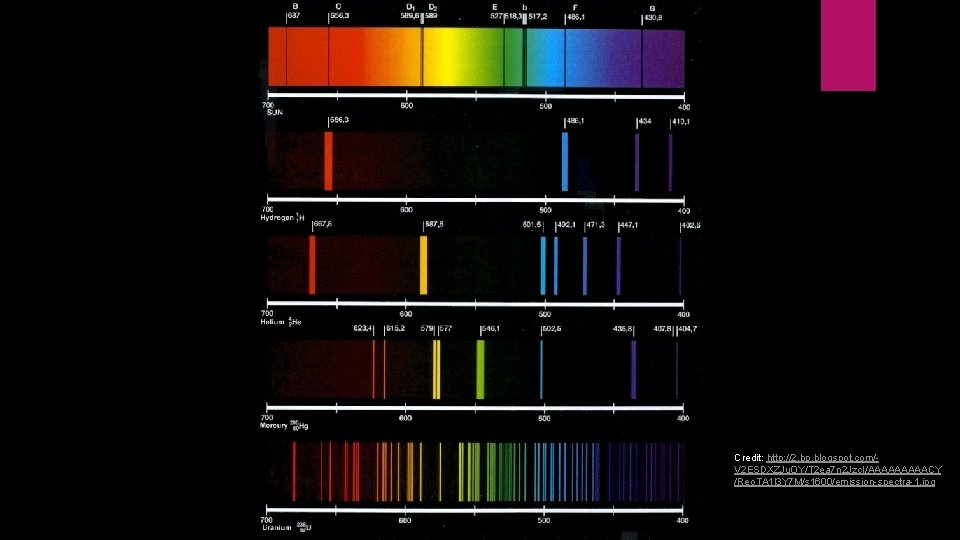
Credit: http: //2. bp. blogspot. com/V 2 ESDXZJu. OY/T 2 ea 7 n 2 Jzc. I/AAAAACY /Reo. TA 1 l 3 Y 7 M/s 1600/emission-spectra-1. jpg
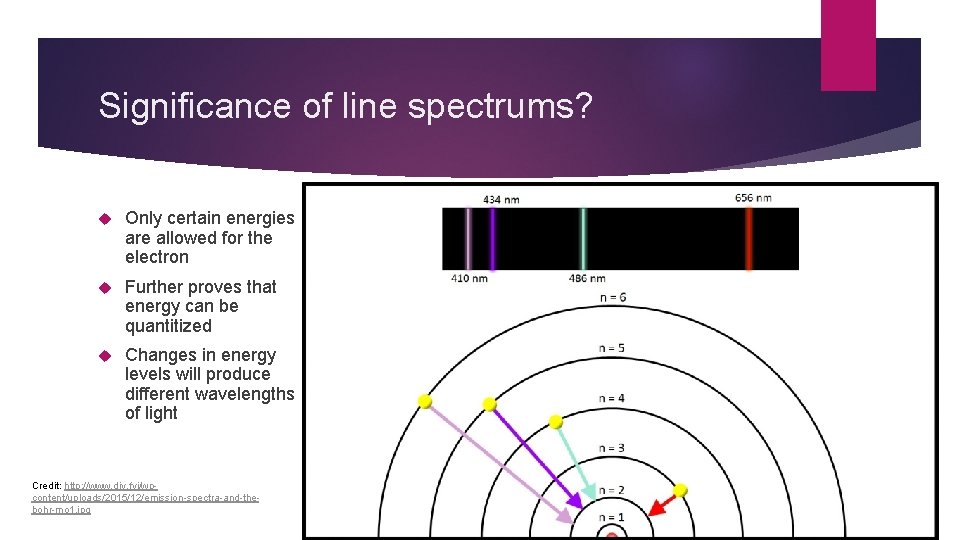
Significance of line spectrums? Only certain energies are allowed for the electron Further proves that energy can be quantitized Changes in energy levels will produce different wavelengths of light Credit: http: //www. diy. fyi/wpcontent/uploads/2015/12/emission-spectra-and-thebohr-mo 1. jpg

Electrons and Energy Levels Ground State: electrons are in low energy levels close to the nucleus Excited State: energy added to the atom allows electrons to jump to higher energy levels When energy stops being added, electrons fall back to ground state They release energy when they do this in the form of light The higher the energy level, the greater the frequency of light released This is what creates the line spectrum

Problems with Bohr’s Model Only mathematically worked for hydrogen Assumed electrons were in fixed orbits, not 3 D orbitals Couldn’t explain how electrons interacted to form bonds Orbits were fixed and did not account for radiation within them Didn’t agree with Heisenberg’s Uncertainty Principle: we cannot know the exact location of an electron So why is this important if it explains so little? Electrons exist only in discrete energy levels Can only move between energy levels by gaining or losing energy

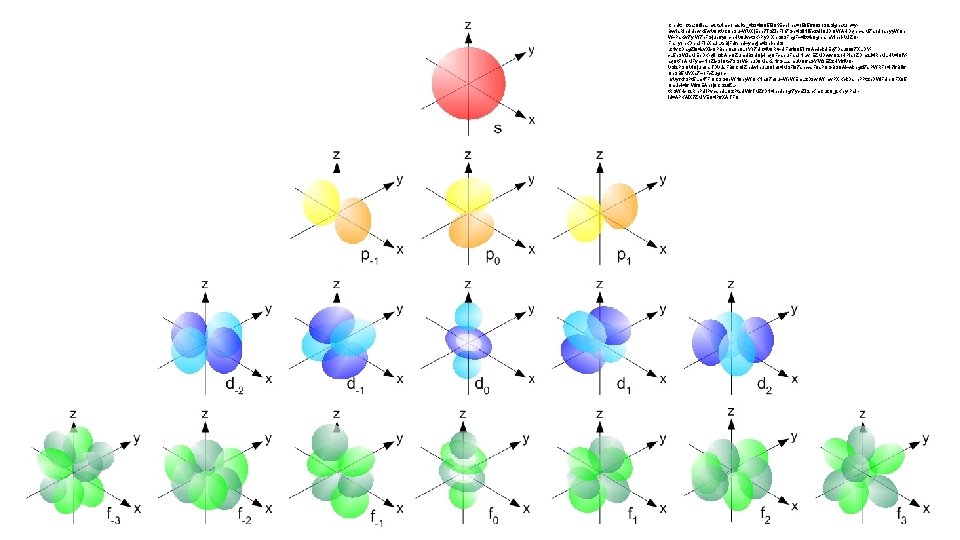
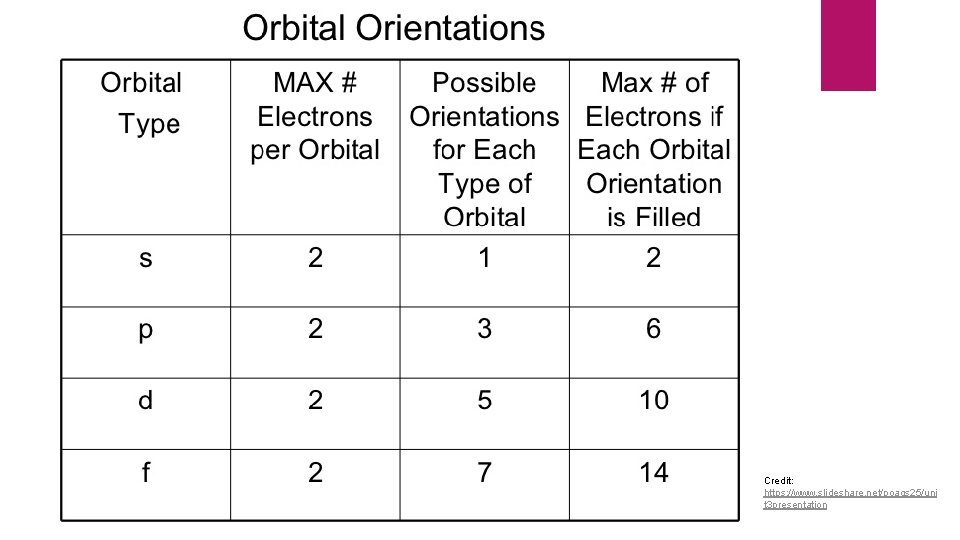
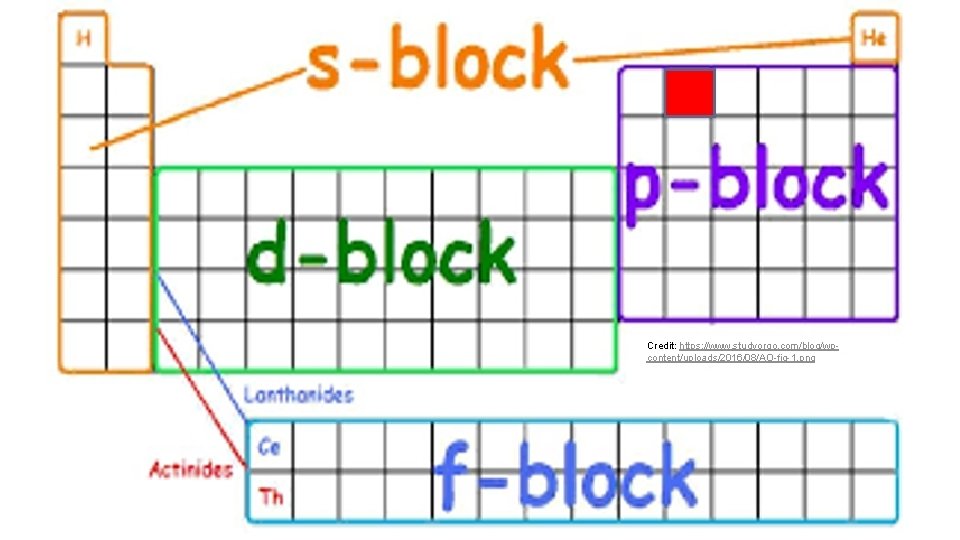
Orbitals 3 D spaces that hold electrons Four categories Multiple shapes 5 subshells s orbital: lowest energy 2 e- in each subshell (10 total) Sphere shaped No subshells Holds two electrons p orbital: second lowest energy Dumbbell shaped 3 subshells Each subshell holds 2 e- (6 total) d orbital: second highest energy f orbital: highest energy Multiple shapes 7 subshells 2 e- in each subshell (14 total)
Credit: https: //files. mtstatic. com/site_4334/8855/0? Expires=1505680313&Signature=y. Bvvia. Rih. UUbw. K 5 w. V 8 ot. VC 0 e. Su~WVXj. Eeb 7 T 3 Zlb. FI 17 Gp 4 Sl. INi 5 xzv. Il. QJDOWAHDqnn~s. M 7 ao. Uospyy. WQb W~Ps. Kw 7 yr. W 7 n. FGjup 6 y 9 h-h. HV 8 Jvxt 3 K-Py. Dr. Xe. S 83 Fpg. F~4 kt 4 b 9 gnhsm. Yihpl-VJZQFhsry 1 h. KDen. JFIh. Xrs. JLtb. Bj. Fdfphd~ymqjm 43 pl-b. Uz. Lt. Nv. CDag. Zi 94 av. XIx 9 PBbe. Os 8 b 9 Lo. Y 17 cl. C 4 V 8 Rt~UFa 6 i 085 inf 0 Acdck. UEq 7 Dau 8697 XLDYx. L 5 p. SWJs. MEp. DK-qi. Intfk. An-QZumd. B 3 d. Qjxlnq. OFxaeu. Fae. JNLwr. EZMDww. Q 2 o. HPla 1 ZDm 2 J 4 Rn. MLHV 4 Ol. Yaq. Qt. F 1 AMFym~No. Zlx. Si. Otc 7 SS 1 Wxnu. D 0 Ma. Ks. Nf. GLLsmu. VQ 6 a. GYW 3 EZz. HY 6 l. VOVSl 2 PSOVIQjuh 9 rs. TDVJs. FB 9 CQIZn. Uwihu. LO 0 Ih 04 MSFi 07 shcxs. F 0 s. PQGBS 0 Al~wkegf. J 7 s. PWRF 14 r 76 Bii 6 On. SB 5 MYXa 7~o. Fx. Zugobhv. Vyf. Kf. SPt 5 Lmt 7 Fr. QC 3 G 9 p. WN 8 ey. WQKNa 07 h 8 u~Wb. WEm. Lz. D 3 wo. Wrpw. PXKck. Dsrn. PPtzn. DWl. FUp. QFX 85 Qm. Jcl-46 r. W 60 EAeoj 8 CS 26 ZLt. RSWHxo 2 Rh. PUIPvcah. ULQz. Pta. UW 6 TMZf. DN 4 npdp 1 gf 7 ycp. ZI 2 h. Km. Cu. C 8_&Key-Pair. Id=APKAIX 7 ZMYEQ 4 P 6 XATFQ
Credit: https: //www. slideshare. net/poags 25/uni t 3 presentation
Credit: https: //www. studyorgo. com/blog/wpcontent/uploads/2016/08/AO-fig-1. png
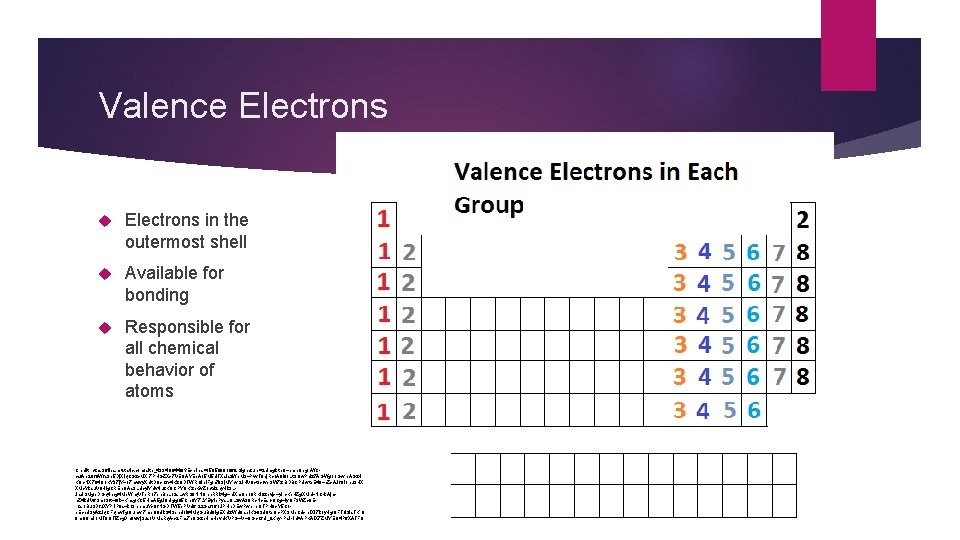
Valence Electrons in the outermost shell Available for bonding Responsible for all chemical behavior of atoms Credit: https: //files. mtstatic. com/site_4334/8844/0? Expires=1505680166&Signature=2 Umgktn. Q~pme. Oegh. WCcsf. Ap 2 Of 6 Wfa 3 b 5 Dj. XIq. CGzx. MXr 7 PHGZXx 7 VEQAYEp. A 15 M 5 d. TXaiaz. Wb. M 3~Pvv. T 9 dj. Rco. A 0 l 9 o. Lt. SQw. PUz 7 AGWg 1 o. Gwrp. AGz. H KQc. NX 794 Oo. KY 37 j. Y~17 nwwy. XUt. DOx. Cfx 4 Kz. QDTWROIb. IFgn 793 j. MYev. SJHV 9 ctoxfvb. SW 7 zr. BDBCPUwtb. E 49~b. Zx. AJf. Ol 1 nu. SHX XMx. Yksu. V 0 Hig. CREn. OAa 3 LUcyl. Ydwtiuz. KOCPYOKzh. Kw. Zoctd 2 ny. Hk 3 LJa. USMgb. DGq 4 ncg 4 Mp. Wnq. VTe. Ro 7 pn. Bn. Lo 2 s. Lw. RS 0 NNOhh. RRk 4 g~nl. Xm. Opo 0 RKi 9 zevjx~y. Irc. Ke. HZg. XMd~NC-k. Ajmh. Z 4 k. UV 6 Sm 13 ft~f 0 k~Knag. KC 5 Hm. A 5 g. J 8 d-gg. O 5 Ch. QY 7 LYEtylp. Pys. LQLzw. A 39 Rc. Nc. Es 1 -9 Cg~Iy. OF 3 WZc 8 Er. Cs 1 Bu. SDfu. XYPrl. P 8 s~k 13 hhmu. Yx. Of. NGDTW 5 b. PVU 6 r 22 Gaf 161 JPHh. DEw. Pwprhr. OTPH 9 x. Y 5 Coe. Ecbd. Sy. Az. Jq. CFqmv. Tg. Oumvr 7 mb. O 8 Uk 34 Send 1 l 04 Mq. Gu. Bd 9 Ig. EXpiz. WU 9 apl. KG 93 d. Qte. Oc. PXSMp. Cdxrpl. XI 7 koy. Hg. QFTolz. Ia. TKn 9 9 m. Q 9 n. Uo. MT 8 OTIZcg. Dn 9 vwj. Sus 1 VMa. Rq. A-x 2 Fns 7 b 8 Gzh. Hm. Hpvd. KVPG~V~OGc. Cfp. I_&Key-Pair-Id=APKAIX 7 ZMYEQ 4 P 6 XATFQ

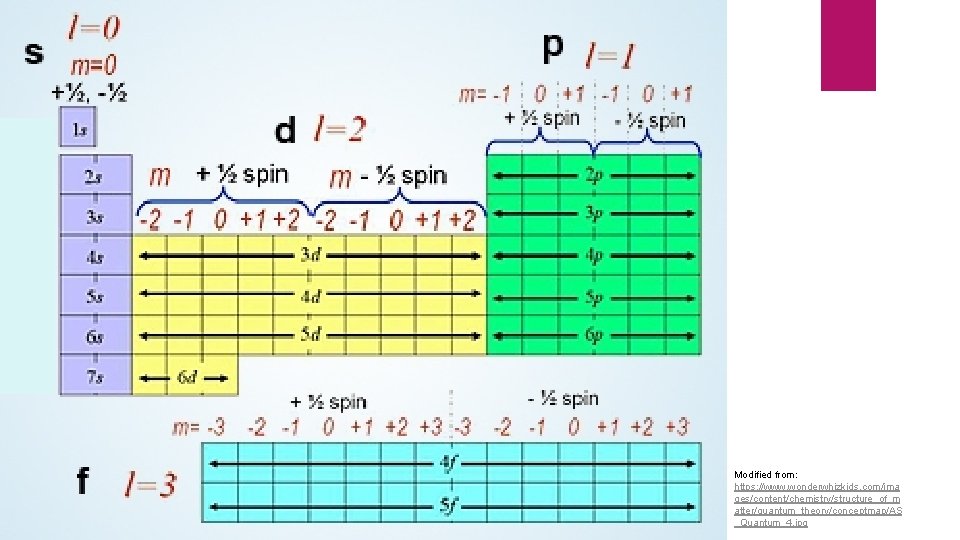
Quantum Numbers Used to describe properties of where valence electrons are and what they are doing Specifically: the last electron in an element Four quantum numbers: Principle (n): energy of an orbital Angular momentum (l): shape of the orbital Magnetic (ml): orientation of the orbital in space Spin (ms): direction the electron is spinning

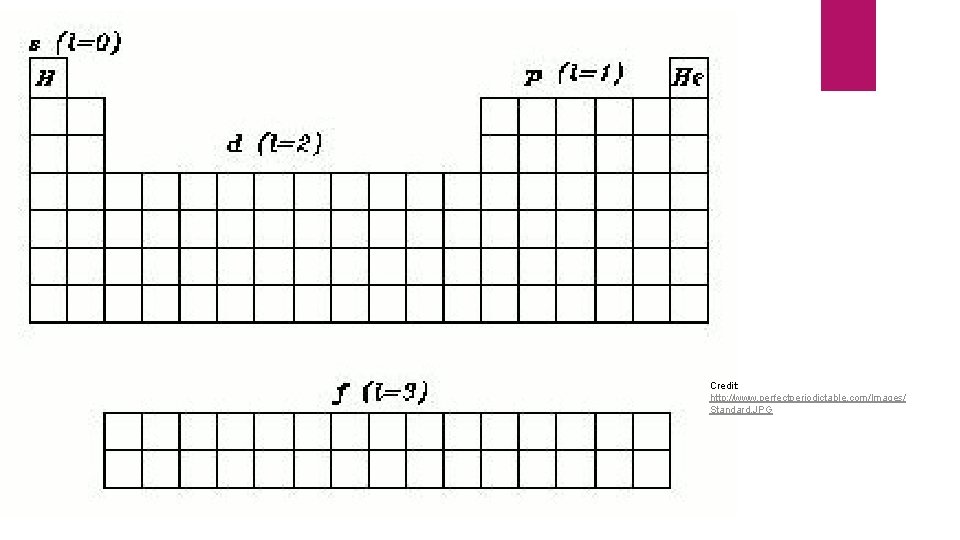
Principle Quantum Number (n) Size and Energy level n = 1, 2, 3, 4, … Currently, we only know of 7 energy levels (periods 1 -7) and four size levels (s, p, d, f) s: n = 1 p: n = 2 d: n = 3 f: n = 4 If we discover more elements, another level and orbital will be added to the periodic table

Angular Momentum (l) Represents the shape of an orbital l = 0: sphere (s orbital) l = 1: dumbbell (p orbital) l = 2: d orbital l = 3: f orbital Always equal to n-1 For each of the principle quantum numbers n = 1, l = 0 n = 2, l = 1 n = 3, l = 2 n = 4, l = 3
Credit: http: //www. perfectperiodictable. com/Images/ Standard. JPG

Magnetic Quantum Number (ml) Credit: http: //www. chemtube 3 d. com/images/Alevel-porbitals. jpg Orientation of the orbital in space Easiest to observe with the p orbital:

Magnetic Quantum Number (ml) For each l there are rules: ml can be any number from –lto + l For the s orbital: l = 0, so ml can only = 0 For the p orbital: l = 1, so ml can = -1, 0, +1 For the d orbital: l = 2, so ml can = -2, -1, 0, +1, +2 For the f orbital: l = 3 so ml can = -3, -2, -1, 0, +1, +2, +3 Which number an element has depends on where it is on the periodic table
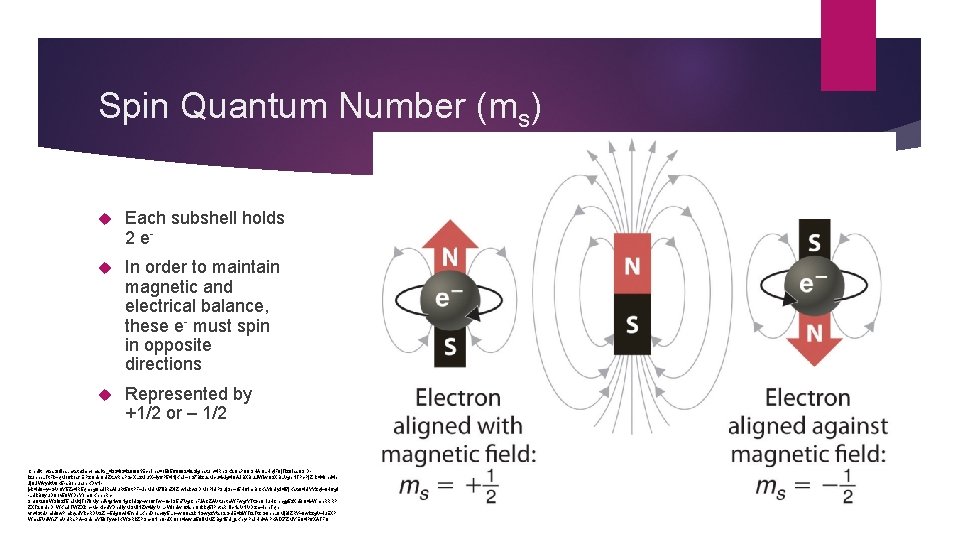
Spin Quantum Number (ms) Each subshell holds 2 e- In order to maintain magnetic and electrical balance, these e- must spin in opposite directions Represented by +1/2 or – 1/2 Credit: https: //files. mtstatic. com/site_4334/34206/0? Expires=1505688824&Signature=i. Rp 3 K 2 Qa. P 9 OSHAOLHqi. F 0 j. Tlz. OIss 8 Sr. Dlzuhne. LTt. Fk~q. Mo 6 k 1 sfr. EPz. Qde. QUZt. Lv. Ra. PSx. XLz. Muf. X~Iy 6 P 54 Nj. Ka. J~1 S 7 BIzus. Mcu 4 c. Jg 4 OAJBXBu. Li. Wlw. O 3 XBLVgp. NTPx. Pj. Zhk 448 hd 4 p Jj. OJWvydt. V 8 K 5 -s. Boeua 1 e. KDv. Njxk 4 U 9~y~GVQY 5 Zx 4 R 5 qmeg 0 a. Ui. Rs. AIu. Rt 5 Qt. PF~Jb. MUM 7 ll. Bc. Zti. Zhw. Iakw 3 DMo. Pi. UP 3 uj. Se~o 5 H 6 ihp. BCKs. Y 8 Uy. J 4 l 7 j. Katc 04 UYYzql~9 H 6 g. I -LUk. B 0 yu. DQov 59 WDe. Yom. QKbnh. Rb 3 no 9 t 208 WSi 8 z. T 5 h. JMtj. To 70 Myhd. Atg. Nw 9 Ng. Ci. Uzy~wof 6 Tw~Ox. IS 5 h 7 Vg. Ch. FJACZAVtuetm. WFwgf. YTt. Ge 0 r. Iu. HCnhgg 5 z. Xd. BO 4 c. Wmh. RRRP ZXT 2 QUe. Dr. WKa. UTWZXkh~Mx. Klcd. YDp. Uly. MSMl. NZv 4 dyr. Vr. L-Wlodwhztlse. Qokkq 5 IPcta. Rri. Ic. Ns. VNVDzm~ipn. Tqnvfc 4 Sta. Vmld 9 w. Pmkqsd. Ykc. RDV 2 Zr~5 dg. Qw. It 5 fe. ULKpd. Dosc 6 y 5 L 1~w. Q 0 a 2 k. NGwyz. Ytao 2 Gai. E 4 z. WTf 2 Tt. CG 9 bn. L 9 Mj. Bl. ZRY~9 wkzg. V~iu. EXP Wms 5 Vd. Ws 7 m. VURs. PA~3 dpm. Y 50 Tywx. IKWGRk. ZP 3 nx 0 Nh. Q-d. XOoo 4 wwuf 58 l. IMMZBg. N 5 U_&Key-Pair-Id=APKAIX 7 ZMYEQ 4 P 6 XATFQ
Modified from: https: //www. wonderwhizkids. com/ima ges/content/chemistry/structure_of_m atter/quantum_theory/conceptmap/AS _Quantum_4. jpg

Assigning Quantum Numbers For each of the following elements: assign the four quantum numbers: Na, Br, O, At, Cu, Os, U, Eu

Electron Configurations Quantum numbers tell you about the last electron Electron configurations tell you about every electron that an atom has (which orbital it’s in) Electrons occupy orbitals in order of lowest to highest energy. Credit: http: //www. mrphysics. org/images/elecfill. gif
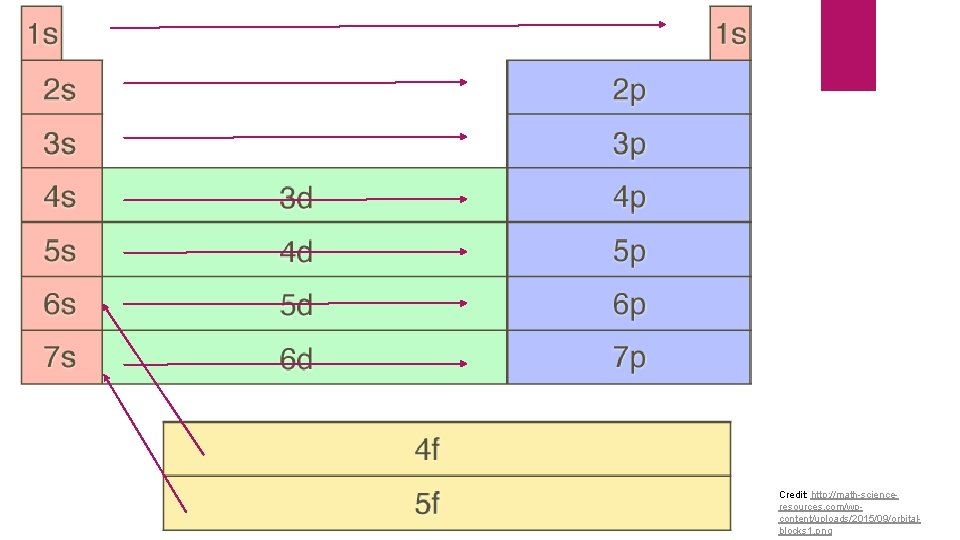
Credit: http: //math-scienceresources. com/wpcontent/uploads/2015/09/orbitalblocks 1. png
Rules Electrons Follow Pauli’s Exclusion Principle: in a given atom no two electrons can have the same set of four quantum numbers Aufbau’s Principle: electrons will occupy the lowest energy orbit available Hund’s Rule: each subshell of an orbital will receive one electron before they start filling up

Types of Electron Configurations Orbital Notation: uses arrows to represent electrons Longhand notation (sometimes just called electron configuration) 1 s 22 p 3 Noble gas notation [He]2 s 22 p 3 Credit: http: //www. yourfavoritewebsite. net/IBChem/Chapter 0 8/Images/Orbital. Notation. gif

Example 7. 7 p. 328 Give the electron configurations (all three) for sulfur, cadmium, hafnium, and radium using the periodic table. Sulfur: Cadmium: Hafnium: Radium:
#85 p. 345 The elements Si, Ga, As, Ge, Al, Cd, S, and Se are all used in the manufacture of various semiconductor devices. Write all three electron configurations for each of these elements.

Ionization Energy Ion: an atom or group of bonded atoms that has a positive or negative charge Ionization: any process that results in the formation of an ion Ionization energy: energy required to remove one electron from a neutral atom of an element Period Trends Ionization energies increase from groups 1 -18 Group Trends Ionization energies decrease from Period 1 -7

Removing Electrons from Positive Ions If there is enough energy, electrons can be removed from positive ions as well as neutral atoms Energies for removal of 2 nd and 3 rd electrons are called 2 nd & 3 rd ionization energies The more electrons you want to remove, the more energy it takes Shielding is diminished with each removal (fewer electrons to shield effect of nucleus on outer electrons)
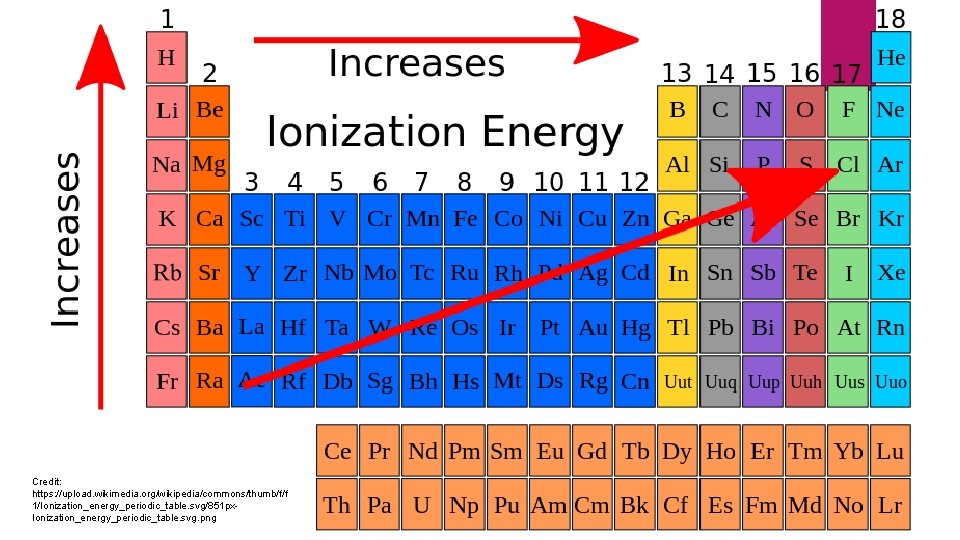
Credit: https: //upload. wikimedia. org/wikipedia/commons/thumb/f/f 1/Ionization_energy_periodic_table. svg/851 px. Ionization_energy_periodic_table. svg. png

#114 p. 346 Rank the elements, Be, B, C, N, and O in order of increasing first ionization energy.

Electron Affinity The energy change that occurs when an electron is acquired by a neutral atom Most atoms release energy when they acquire an electron A few have to be forced to gain an electron by the addition of energy Period Trends Halogens gain electrons most easily Affinities become more negative across each period Group Trends Electrons add with greater difficulty down a group
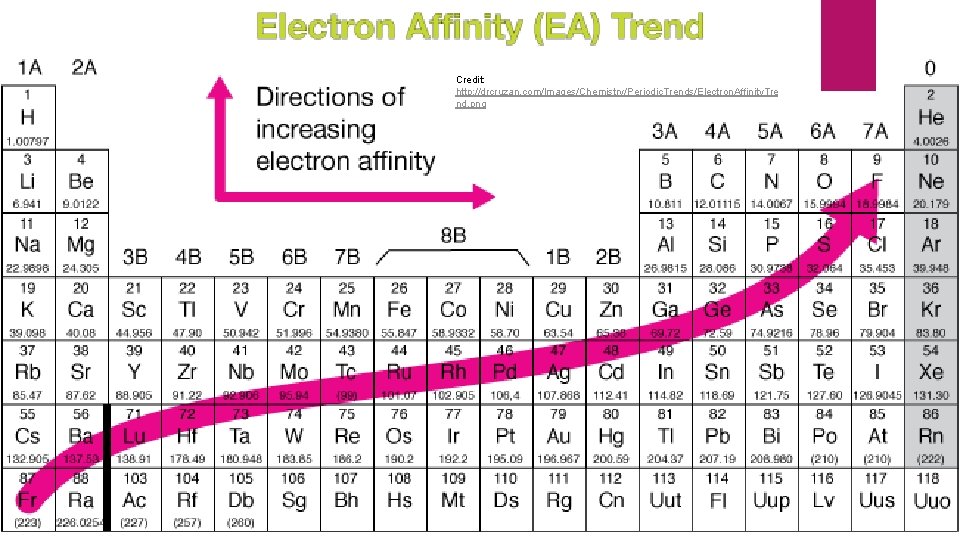
Credit: http: //drcruzan. com/Images/Chemistry/Periodic. Trends/Electron. Affinity. Tre nd. png

Atomic Radii Atomic radius: one-half the distance between the nuclei of identical atoms that are bonded together. Period Trends Radii decreases from group 1 to group 18 As the positive charge in the nucleus increases, the electrons are pulled closer Group Trends Radii increases from Period 1 to Period 7
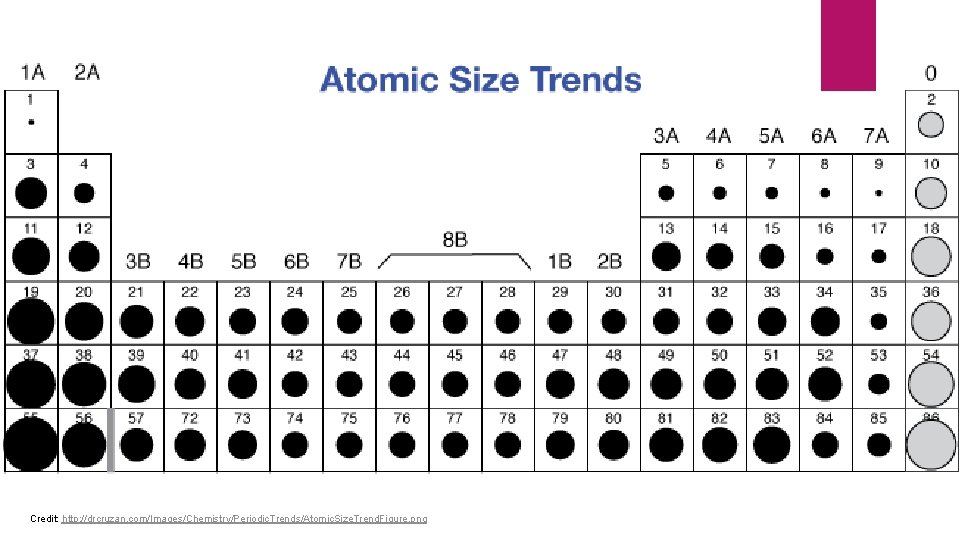
Credit: http: //drcruzan. com/Images/Chemistry/Periodic. Trends/Atomic. Size. Trend. Figure. png

#105 p. 346 Arrange the following groups of atoms in order of increasing size. Te, S, Se K, Br, Ni Ba, Si, F

Electronegativity: a measure of the ability of an atom in a chemical compound to attract electrons from another atom in the compound Period Trends Tend to increase in electronegativity from Group 1 -18 Group Trends Tend to decrease from period 1 -7
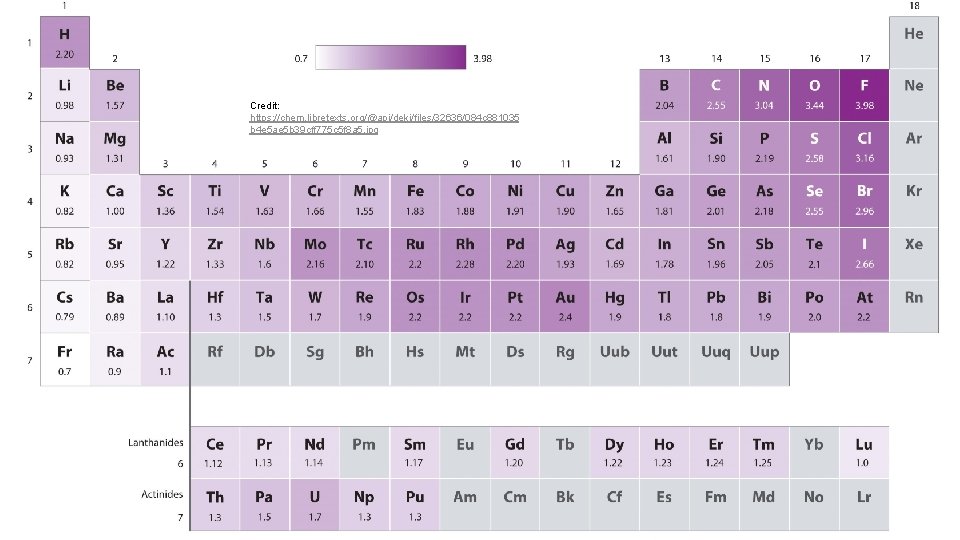
Credit: https: //chem. libretexts. org/@api/deki/files/32636/084 c 881035 b 4 e 5 ae 5 b 39 cff 775 c 5 f 8 a 5. jpg

#117 & 118 p. 347 For each of the following pairs of elements, pick the atom with the (a) higher electron affinity, (b) higher ionization energy, and (c) larger size. C and N Ar and Br Mg and K F and Cl
- Slides: 61