Atomic Spectra Lab 1 Light If we pass

Atomic Spectra Lab 1

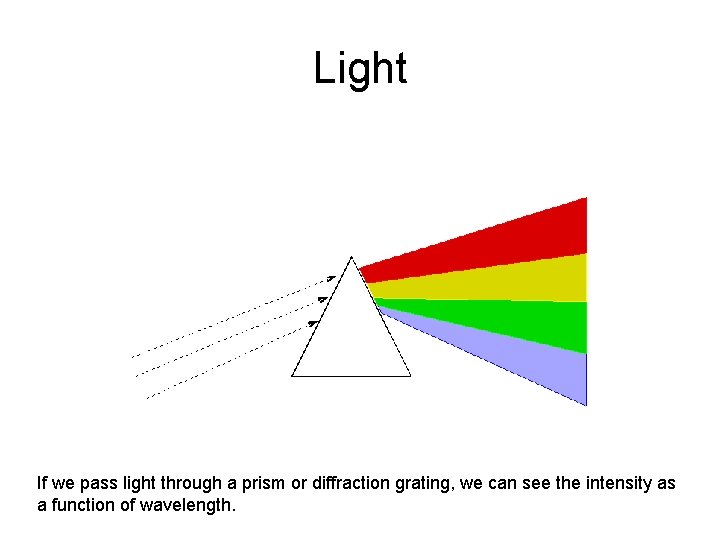
Light If we pass light through a prism or diffraction grating, we can see the intensity as a function of wavelength.

Type of Spectrum Solids, liquids, and dense gases emit light of all wavelengths, without any gaps – or a continuous spectrum

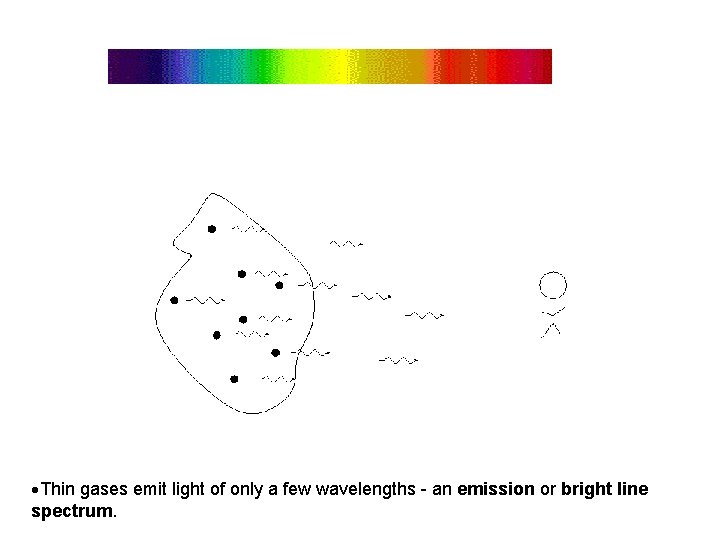
Thin gases emit light of only a few wavelengths - an emission or bright line spectrum.

If there is a source of light behind it, a thin gas will absorb light of the same wavelengths it emits this is called an absorption or dark line spectrum.

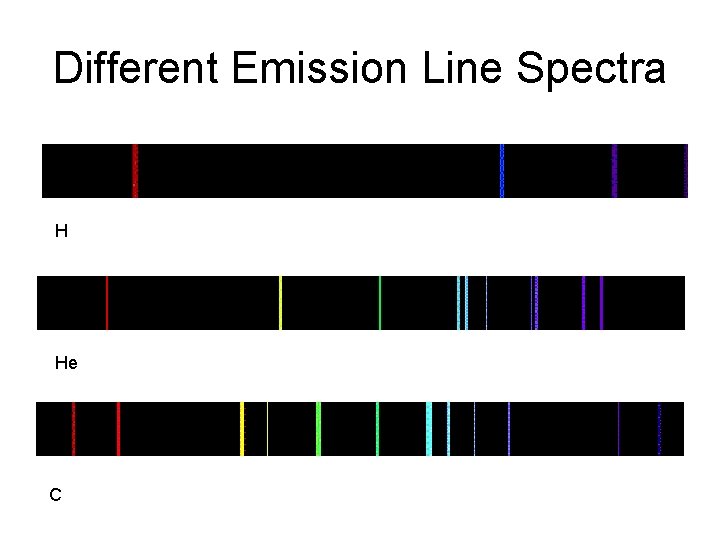
Different Emission Line Spectra H He C

Balmer lines • each element generates its own unique set of wavelengths of emission or absorption • Balmer studied the optical spectrum of hydrogen and found a pattern in the wavelengths of its emission lines

Periodic Table of Elements

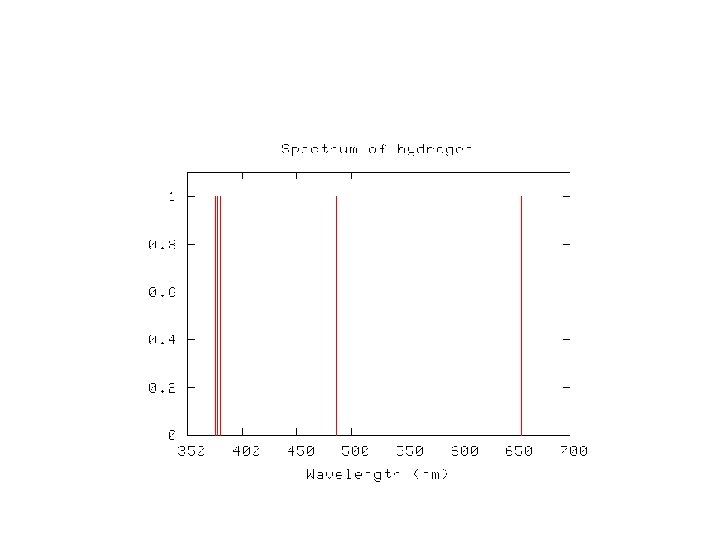
Balmer series – set of visible lines in H spectrum • For H, the wavelengths are - 374. 9 377. 0 379. 7 383. 4 388. 8 396. 9 410. 1 433. 9 486. 0 656. 1 • a simple formula reproduces these wavelengths • λ (n) = (364. 5 nm * ( n 2 /n 2 – 4)) where n = 3, 4, 5, …. .

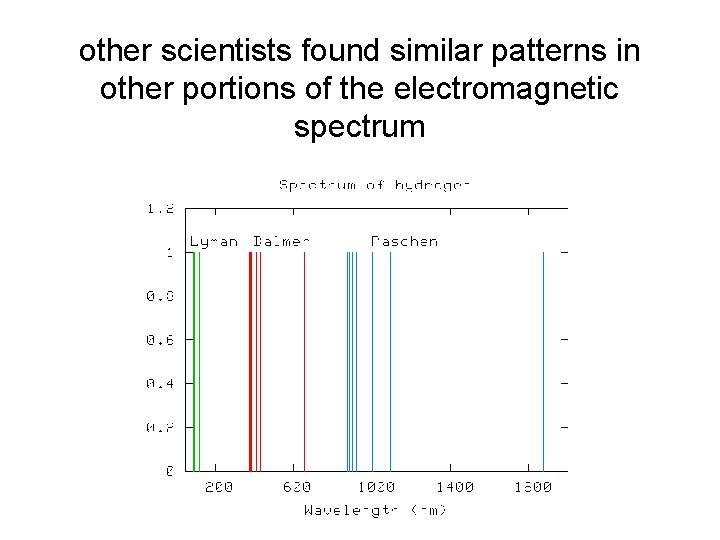
other scientists found similar patterns in other portions of the electromagnetic spectrum

Paschen series • Paschen, in the infrared, measured lines with wavelengths 866. 2 874. 8 886. 0 901. 2 922. 6 954. 3 1004. 6 1093. 5 1281. 4 1874. 5 which matched the series • λ (n) = (820. 5 nm * ( n 2 /n 2 – 9)) where n = 4, 5, 6, …. .

Lyman series • Lyman, in the ultraviolet, a series of lines with wavelengths 91. 9 92. 1 92. 3 92. 6 93. 0 93. 7 94. 9 97. 2 102. 5 121. 5 corresponding to the series • λ (n) = (91. 1 nm * ( n 2 /n 2 – 1)) where n = 2, 3, 4, …. .

• In fact, scientists soon realized that hydrogen's spectrum could be broken down into a large number of series, each of which had wavelengths obeying a formula like • Λ (n, k) = (limit) * ( n 2 /n 2 – k 2)) where n=k+I, k+2, …. • The Lyman series corresponds to k=1 with a limit of 91. 1 nm, the Balmer series to k=2 with a limit of 364. 5 nm, and so forth