Atomic shell model Nuclear shell model each nucleon





















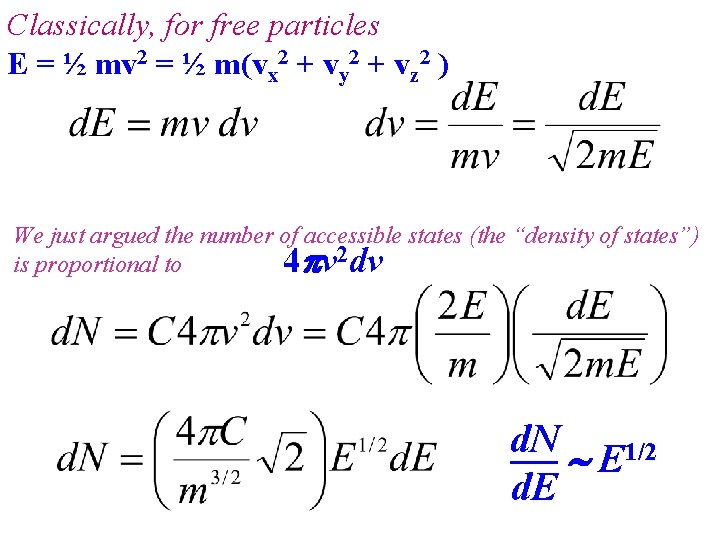






- Slides: 43

Atomic shell model Nuclear shell model each nucleon, separately occupies its own energy level, with each nucleon-type (p, n) filling energy levels separately Each energy level, n exists with an angular quantum number: s p d f g … ℓ = 0, 1, 2, 3, 4, … each with a different angular wave function Yℓ, m( , )

Because of spin (2 possible orientations of each nucleon) any energy level n, ℓ accommodates 2ℓ+1 protons 2ℓ+1 neutrons s: ℓ = 0 coupled with spin: s 1/2 p: ℓ = 1 p 1/2 p 3/2 d: ℓ = 2 d 3/2 d 5/2 f: ℓ = 3 f 5/2 f 7/2 These are different particles – They don’t mutually exclude each other! J=0+½ The total (magnitude) of J is limited to -|ℓ-s|…|ℓ+s| in unit steps!

As an example, there is a 1 f 5/2 energy level that can hold ? ? protons with different mj values and another that can hold 6 neutrons. Consider: 27 13 Al (ground state) 2 4 2 5 2 4 2 6 Protons: (1 s 1/2) (1 p 3/2) (1 p 1/2) (1 d 5/2) Neutrons: (1 s 1/2) (1 p 3/2) (1 p 1/2) (1 d 5/2) 1 un-paired proton with j=5/2 so aluminum: I=5/2

Consider: 9 Be (ground state) 2 2 2 3 p: (1 s 1/2) (1 p 3/2) (1 p 1/2) (1 d 5/2) n: (1 s 1/2) (1 p 3/2) (1 p 1/2) (1 d 5/2) 1 un-paired neutron with j=3/2 so: I=3/2 Consider: 9 B (ground state) 2 3 2 2 p: (1 s 1/2) (1 p 3/2) (1 p 1/2) (1 d 5/2) n: (1 s 1/2) (1 p 3/2) (1 p 1/2) (1 d 5/2) 1 un-paired proton with j=3/2 so: I=3/2

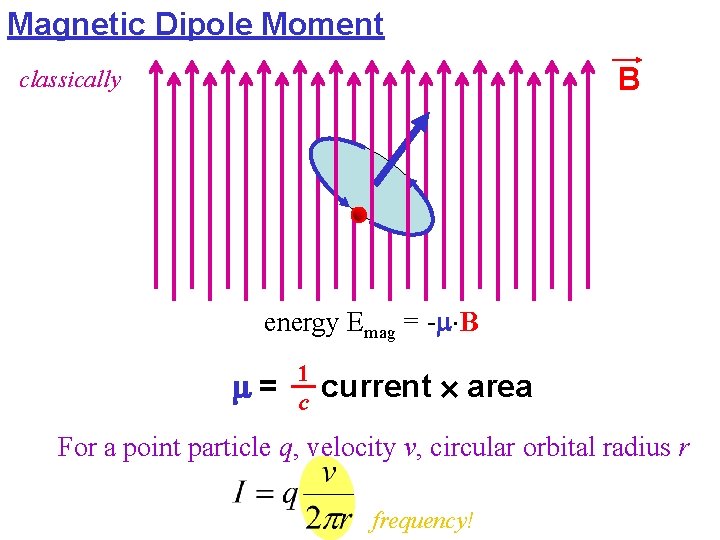
Magnetic Dipole Moment B classically energy Emag = - B = 1 c current area For a point particle q, velocity v, circular orbital radius r frequency!

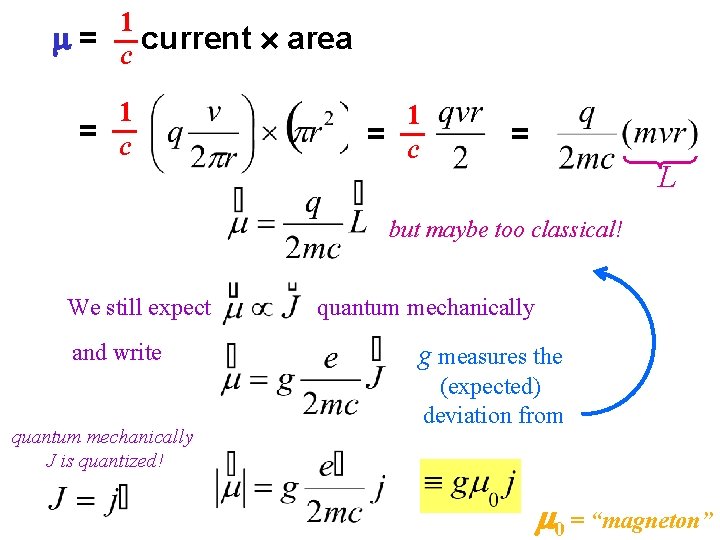
1 = c current area 1 = c = L but maybe too classical! We still expect and write quantum mechanically J is quantized! quantum mechanically g measures the (expected) deviation from 0 = “magneton”

For atomic physics (involving electrons) “Bohr magneton” For nuclear physics “nuclear magneton” For the neutron: g= -3. 826083 0. 0000018 0 !


With this abbreviation: n, l, ml, s, ms, j, … we represent the exact solutions to some time-independent potential (constant Hamiltonian)

Simply a complex phase that oscillates in time. Where you note we used the fact that With En the eigenvalues, and the eigenfunctions which form a COMPLETE ORTHONORMAL SET. ? As long as H is just constant, these are considered stationary states.

Imagine, initially, a particle was in one of the stationary states of H (the simple Hamiltonian with exact solutions). which is NOT an exact solution of some NEW Hamiltonian H + Hint …no reason to expect it to be “stationary” now! Obviously there is the probability of a transition to some OTHER state (decay to a lower energy state, scattering to a new momentum state, or even transmutation into some new particle)!

Maclaurin (or "power") Series Axn Functions that form a COMPLETE ORTHONORMAL SET for x measured in radians (not degrees!)

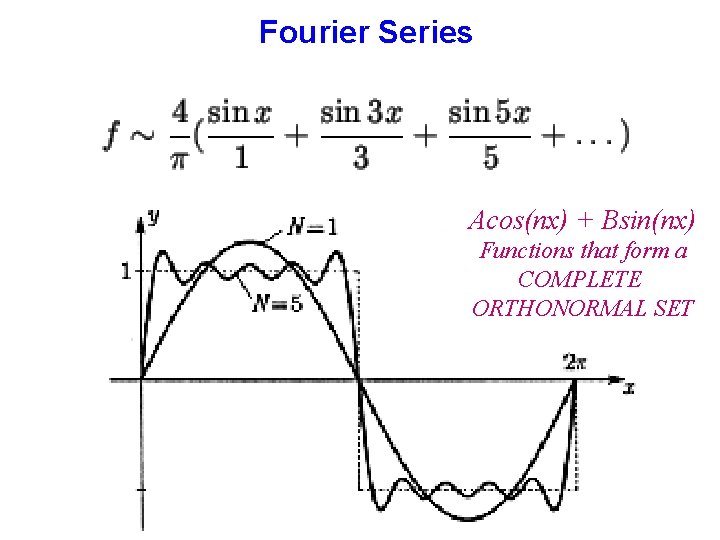
Fourier Series Acos(nx) + Bsin(nx) Functions that form a COMPLETE ORTHONORMAL SET

Imagine a free particle (with an exact eigensolution) of initial energy E Dt ) passes near the source of some potential and is scattered into a final state of energy Em. At time to=0 momentarily ( for a short total time, H H + Hint And now we need to try and solve

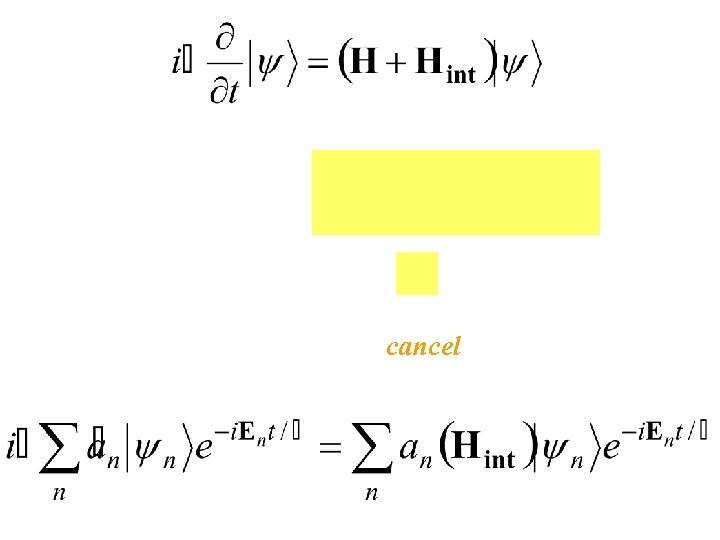
Because the | n> comprise a “complete” orthogonal “basis set” |an(t)|2 probability of finding the particle in state n at time t.

cancel

Initially for t < to = 0 (when Hint=0) 1 0 Vint once t > to = 0 (when Vint , t small) ~ 1 to = 0 1 but not 0 Watch how we can pluck out a specific coefficient by: m m

with the only substantial contribution coming from n=?

We wanted to solve: using, because the | n> comprise a “complete” orthogonal “basis set” |an(t)|2 probability of finding the particle in state n at time t. We found:

If we simplify the action (as we do impulse in momentum problems) to an average, effective potential V(t) during its action from (t 0, t) ≈ Then, for a (short) time T following to: factor out

So the probability of finding this system in a different state m after a time T

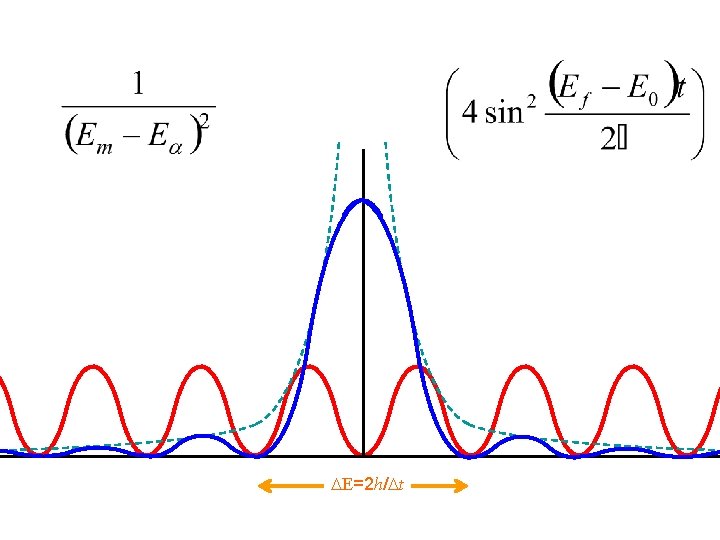
E=2 h/ t

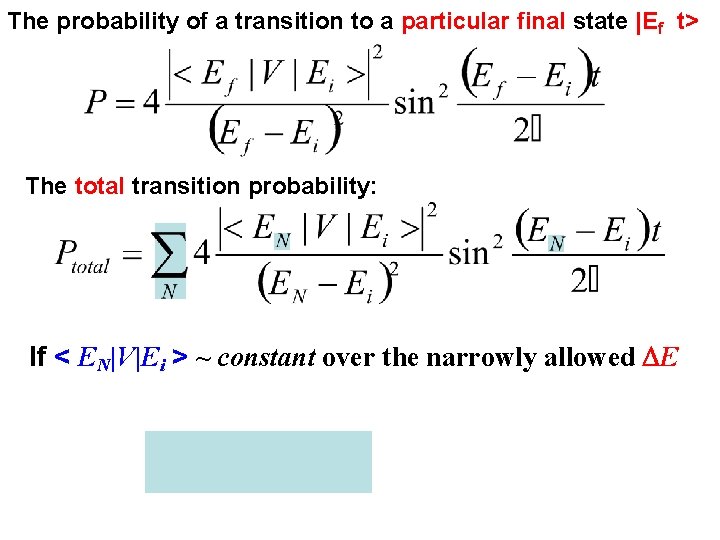
The probability of a transition to a particular final state |Ef t> The total transition probability: If < EN|V|Ei > ~ constant over the narrowly allowed DE

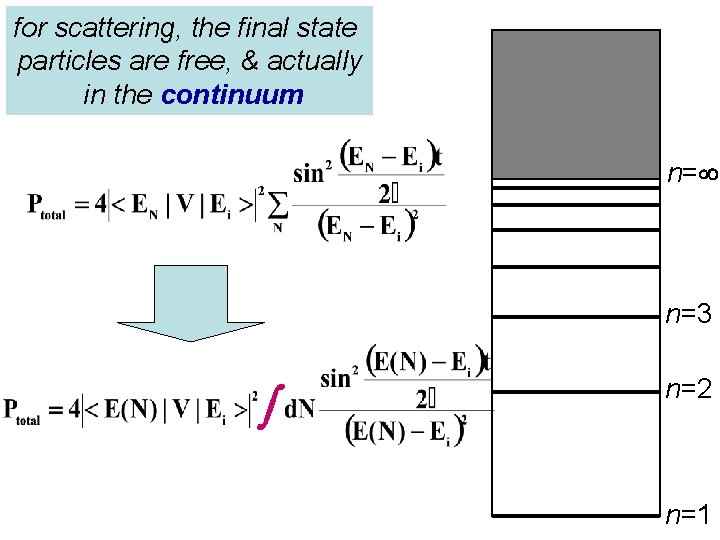
for scattering, the final state particles are free, & actually in the continuum n= n=3 n=2 n=1

With the change of variables:

Notice the total transition probability and the transition rate t

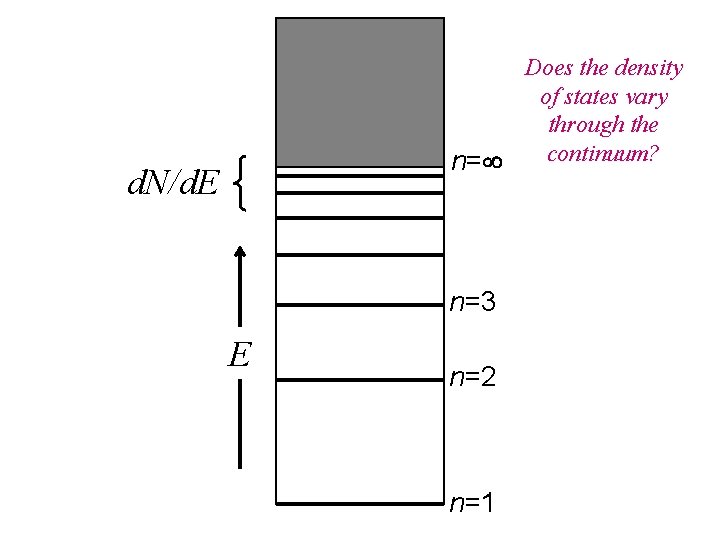
Does the density of states vary through the continuum? n= d. N/d. E n=3 E n=2 n=1


Classically, for free particles E = ½ mv 2 = ½ m(vx 2 + vy 2 + vz 2 ) vz vy Notice for any fixed E, m this defines spherical surface of velocity points all which give the same kinetic energy. vx The number of “states” accessible by that energy are within the infinitesimal volume (a shell a thickness dv on that sphere). d. V = 4 v 2 dv
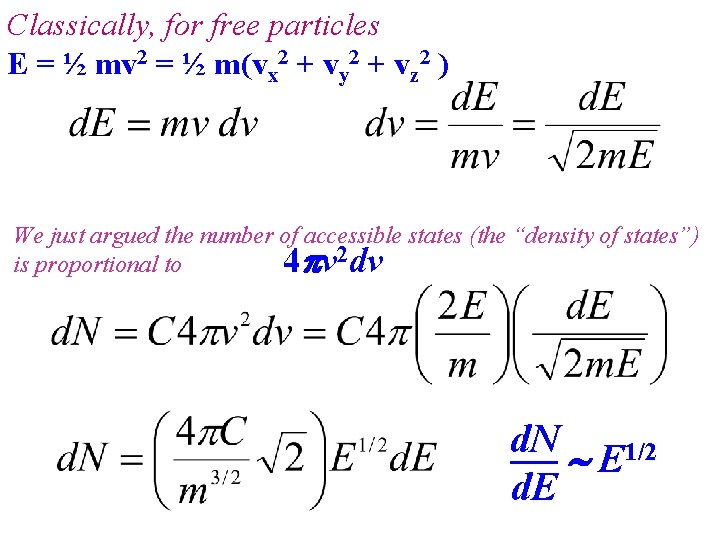
Classically, for free particles E = ½ mv 2 = ½ m(vx 2 + vy 2 + vz 2 ) We just argued the number of accessible states (the “density of states”) is proportional to 4 v 2 dv d. N E 1/2 d. E

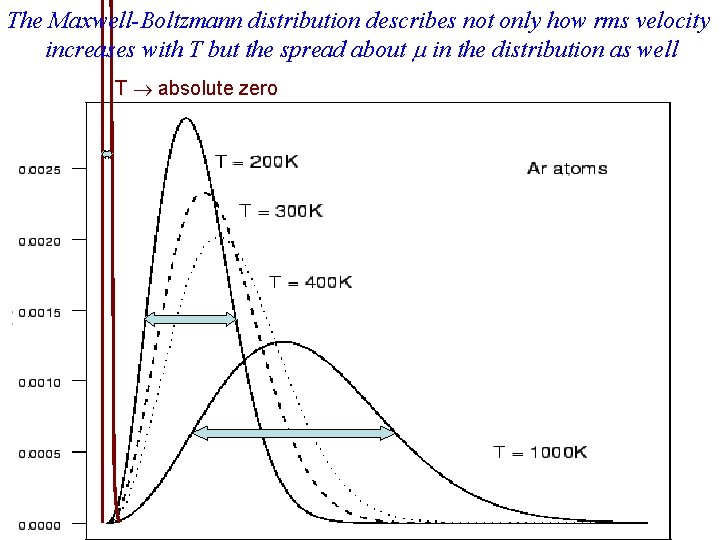
The Maxwell-Boltzmann distribution describes not only how rms velocity increases with T but the spread about in the distribution as well T absolute zero

With increasing energy (temperature) a wider range of velocities become probable. There are MORE combinations of molecules that can display this total E. That’s exactly what “density of states” describes. The absolute number is immaterial. It’s the slope with changing E, d. N/d. E that’s needed.

For a particle confined to a cubic box of volume L 3 the wave number vector is quantum mechanically constrained The continuum of a free particle’s momentum is realized by the limit L

For a LARGE VOLUME these energy levels may be spaced very closely with many states corresponding to a small range in wave number The total number of states within a momentum range

The total number of final states per unit volume or From E=p 2/2 m d. E=p dp/m d. E = v dp

number of final states per unit volume whose energies lie within the range from E to E+d. E Giving (FINALLY) the transition rate of

Since transition rate = FLUX × cross-section or s = rate/FLUX /nvi Particle density of incoming beam but here we’re talking about one-on-one collisions If final states of target and projectile have non-zero spins

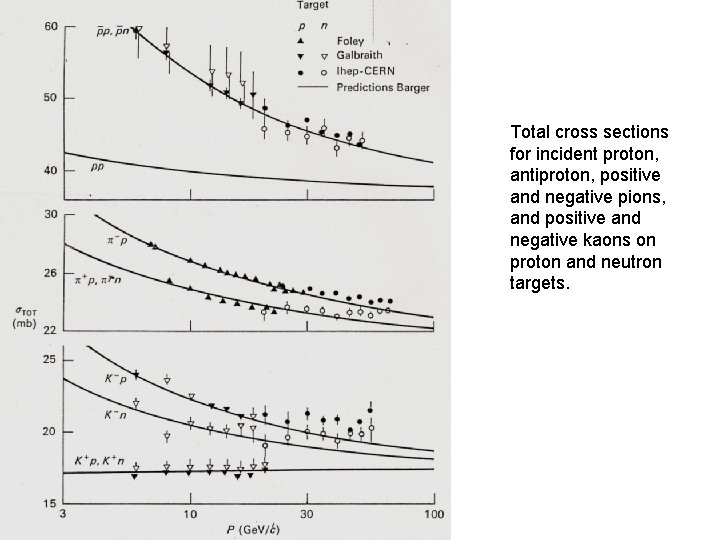
Total cross sections for incident proton, antiproton, positive and negative pions, and positive and negative kaons on proton and neutron targets.

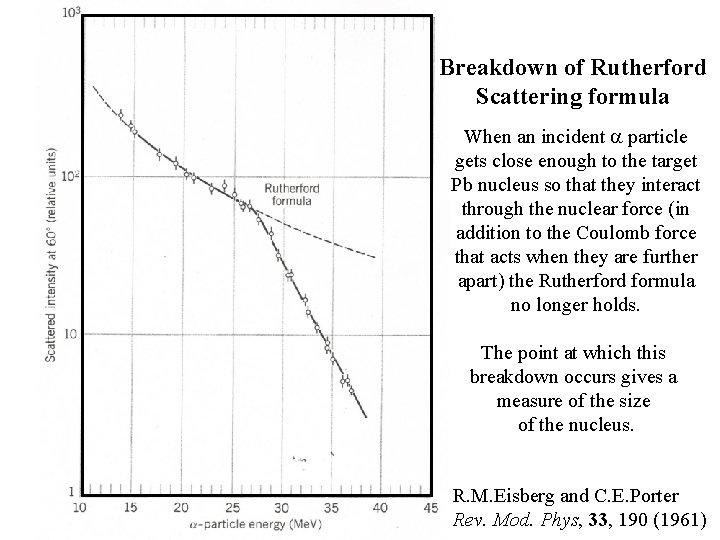
Breakdown of Rutherford Scattering formula When an incident particle gets close enough to the target Pb nucleus so that they interact through the nuclear force (in addition to the Coulomb force that acts when they are further apart) the Rutherford formula no longer holds. The point at which this breakdown occurs gives a measure of the size of the nucleus. R. M. Eisberg and C. E. Porter Rev. Mod. Phys, 33, 190 (1961)

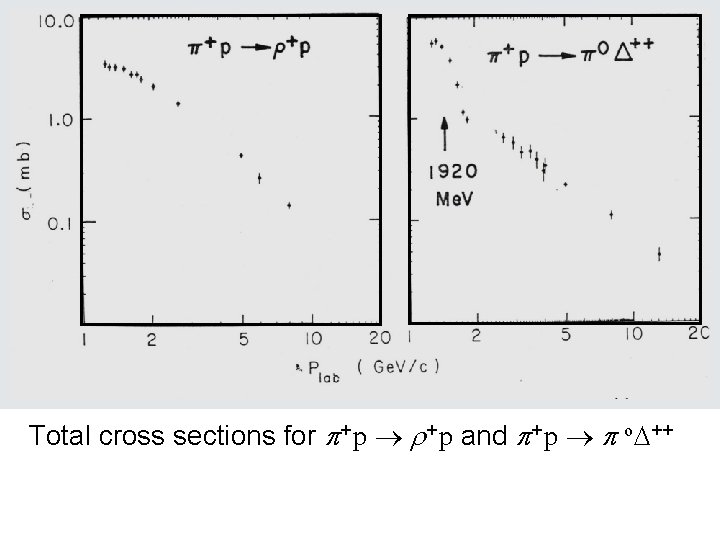
Total cross sections for + p and + p o ++

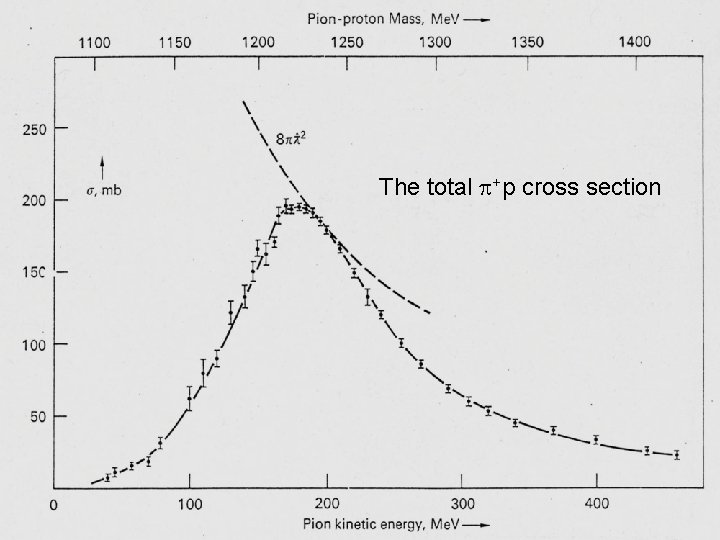
The total +p cross section

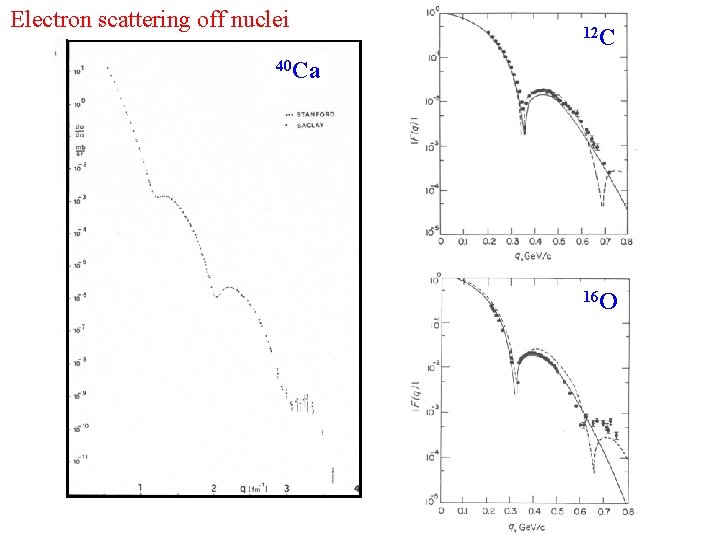
Electron scattering off nuclei 12 C 40 Ca 16 O

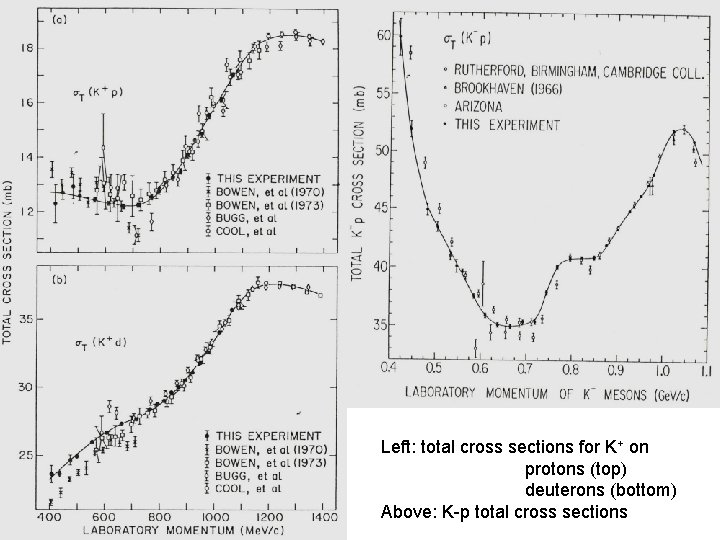
Left: total cross sections for K+ on protons (top) deuterons (bottom) Above: K-p total cross sections