Atomic Orbitals Atomic Orbitals S Atomic Orbitals pz
Atomic Orbitals
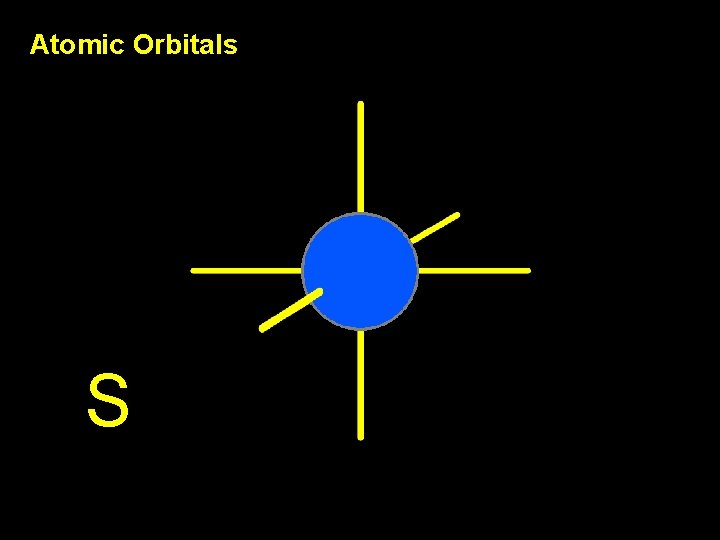
Atomic Orbitals S
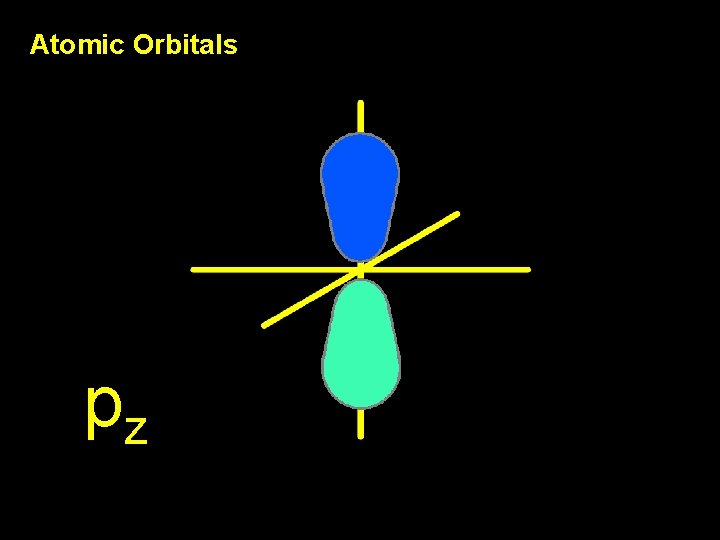
Atomic Orbitals pz
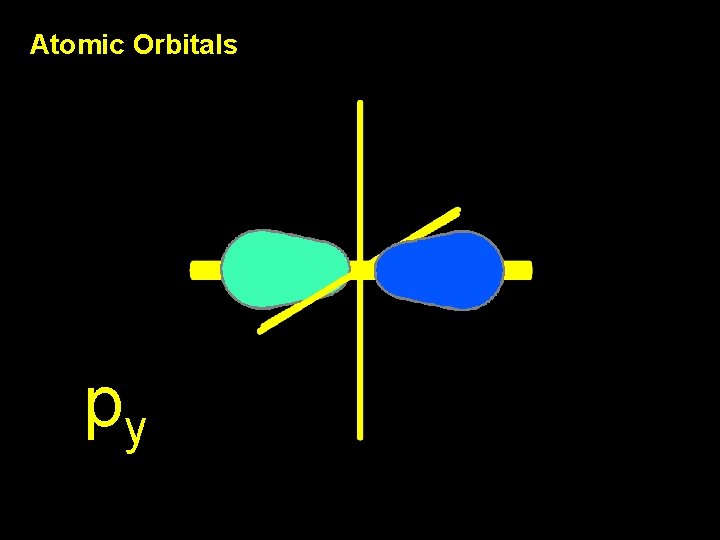
Atomic Orbitals py
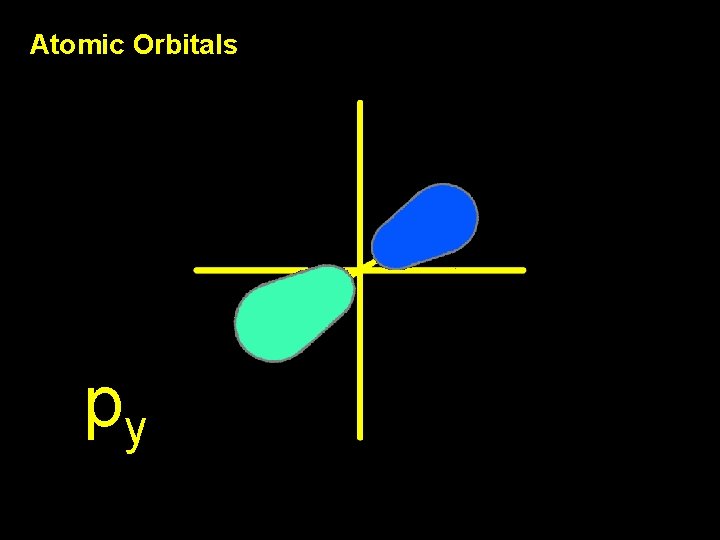
Atomic Orbitals py
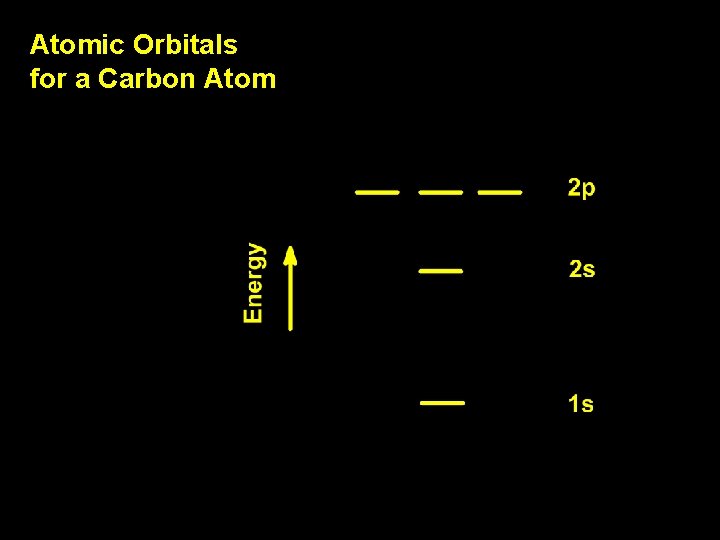
Atomic Orbitals for a Carbon Atom
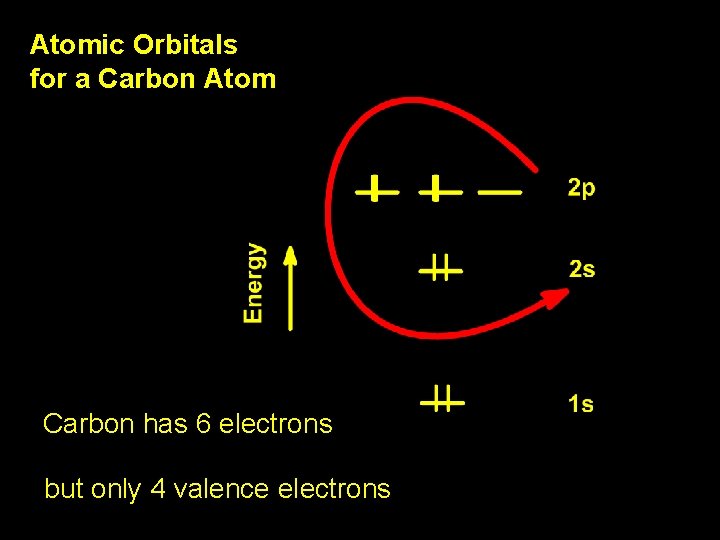
Atomic Orbitals for a Carbon Atom Carbon has 6 electrons but only 4 valence electrons

Where do these orbitals come from? The orbitals are actually mathematical functions that satisfy Schrödinger’s equation. ĤY=EY Ĥ is the Hamiltonian operator that operates on the wave funtions Y to give the Energy E. This is a special form of what is called a wave equation. Y is a wave function, a function that fully describes the electrons of a system in a particular state.

Where do these orbitals come from? ĤY=EY The atomic orbitals 1 s, 2 p etc are wave functions that describe different states of an electron of a atom with one electron. Ĥ F 2 s = E F 2 s

F 2 s describes where we can find the electron Ĥ F 2 s = E F 2 s 2 gives the probability of finding the electron. F 2 s = 1 2 If you integrate over all space the probability is unity. Functions that behave this way are said to be normalized.

E gives the energy of the electron Ĥ F 2 s = E F 2 s You can equate the energy E of the electron to its ionization energy. This is the energy needed for the electron to escape from the atom.

How do you actually calculate the Energy of some wave function Fa ? Start with Ĥ Fa = E Fa Multiply by Fa and integrate F a Ĥ F a = F a E F a = E F a 2 Fa Ĥ Fa = E This is a Coulomb integral Gives E of function F

Another important integral is called an interaction integral. It gives the energy of “interaction” of two different functions. Fa Ĥ Fb = Eint

Now we have the tools we need to describe Molecular Orbitals. We are going to use an approximate method called the LCAO approach. Molecular orbitals, Y, are expressed as Linear Combinations of Atomic Orbitals, F. Y = Sc F i i The coefficients, ci, of each orbital must be determined
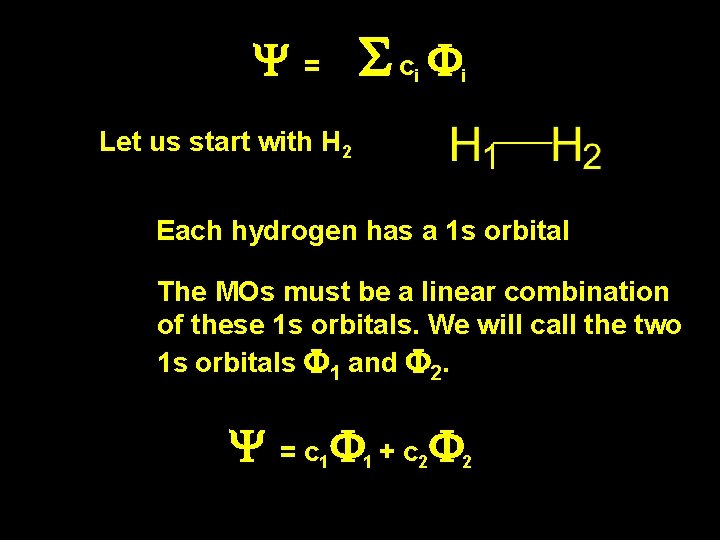
Y = Sc F i i Let us start with H 2 Each hydrogen has a 1 s orbital The MOs must be a linear combination of these 1 s orbitals. We will call the two 1 s orbitals F 1 and F 2. Y = c 1 F 1 + c 2 F 2

Y = c 1 F 1 + c 2 F 2 The H 2 molecule has symmetry, this means that the electron density on one end must be the same as the electron density on the other end. This can only happen if the coefficients c 1 and c 2 are of equal magnitude. There are two ways to do this. Either c 2 = c 1 or c 2 = - c 1. Y 1 = c 1 F 1 + c 1 F 2 or Y 2 = c 1 F 1 - c 1 F 2

Y 1 = c 1 F 1 + c 1 F 2 How do we determine the Energy? First we need to assume some integral values. Let us assume: Coulomb integral Fa Ĥ Fa = E = a = 0 Interaction integral Fa Ĥ Fb = Eint = b
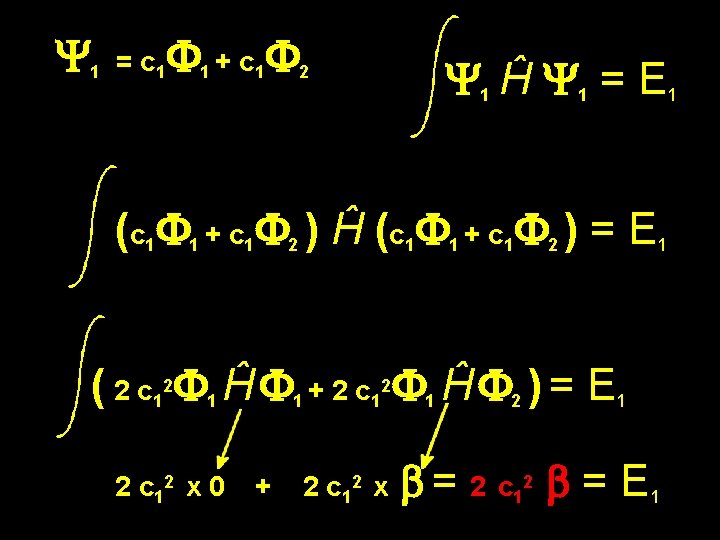
Y 1 = c 1 F 1 + c 1 F 2 Y 1 Ĥ Y 1 = E 1 (c 1 F 1 + c 1 F 2 ) Ĥ (c 1 F 1 + c 1 F 2 ) = E 1 ( 2 c 12 F 1 Ĥ F 1 + 2 c 12 F 1 Ĥ F 2 ) = E 1 2 c 12 x 0 + 2 c 12 x b = 2 c 12 b = E 1

But what is c 1 ? Y 1 = c 1 F 1 + c 1 F 2 Y 1 Y 1 = 1 (c 1 F 1 + c 1 F 2 ) ( c 1 F 1 + c 1 F 2 ) = 1 define Fa = 1 2 Fa. Fb = Sab Overlap integral
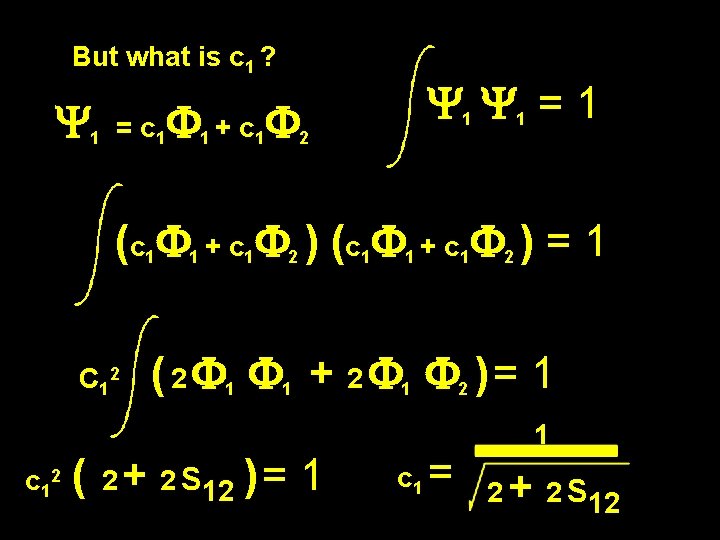
But what is c 1 ? Y 1 = c 1 F 1 + c 1 F 2 Y 1 = 1 (c 1 F 1 + c 1 F 2 ) ( c 1 F 1 + c 1 F 2 ) = 1 C 12 c 12 ( 2 F 1 + 2 F 1 F 2 ) = 1 ( 2 + 2 S 12 ) = 1 c 1 = 1 2 + 2 S 12
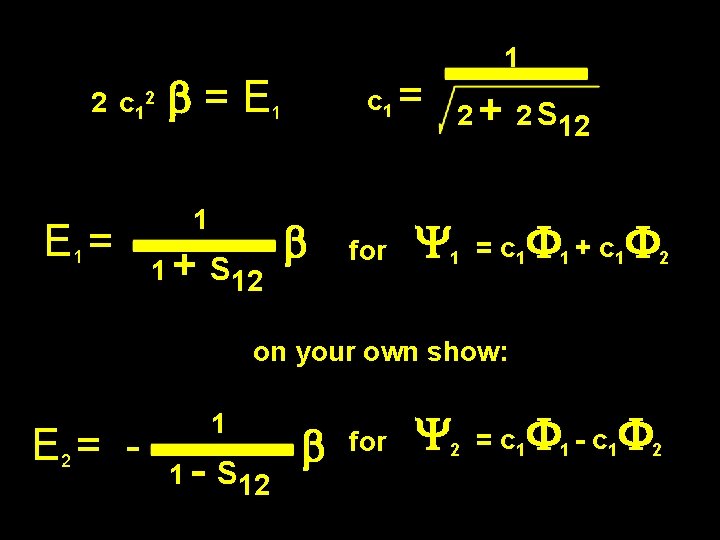
2 c 12 E 1 = b = E 1 1 1 + S 12 c 1 = b for 1 2 + 2 S 12 Y 1 = c 1 F 1 + c 1 F 2 on your own show: E 2 = - 1 1 - S 12 b for Y 2 = c 1 F 1 - c 1 F 2
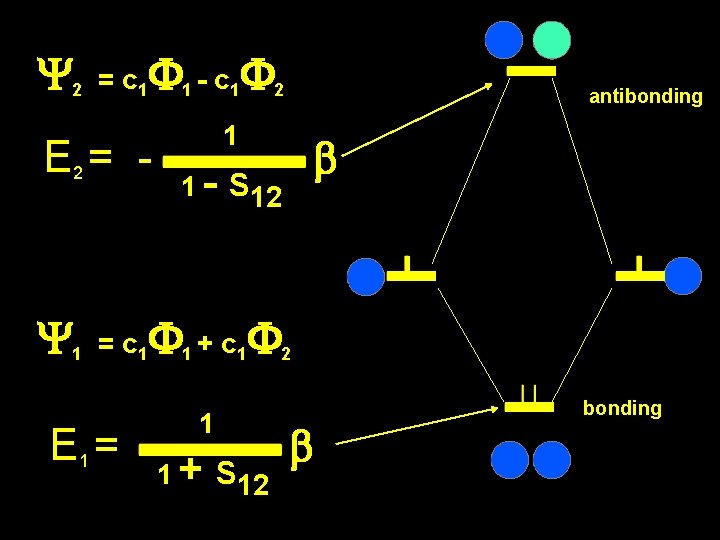
Y 2 = c 1 F 1 - c 1 F 2 E 2 = - Y 1 antibonding 1 b 1 - S 12 = c 1 F 1 + c 1 F 2 E 1 = 1 1 + S 12 b bonding
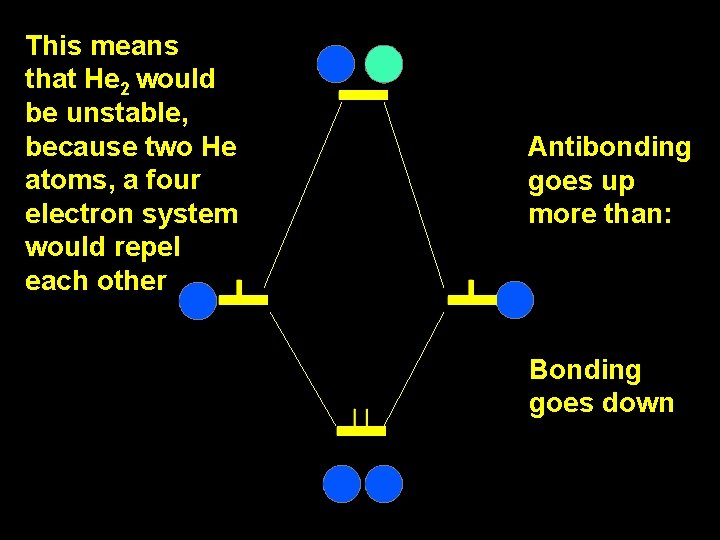
This means that He 2 would be unstable, because two He atoms, a four electron system would repel each other Antibonding goes up more than: Bonding goes down
- Slides: 23