Atomic orbital Hydrogenatom wave function Derivation of hydrogenatom

Atomic orbital & Hydrogen-atom wave function 原子軌道と水素原子波動関数

Derivation of hydrogen-atom wave function @ Schrödinger eq. of H atom（水素原子のシュレディンガー方程式）

Derivation of hydrogen-atom wave function @ Schrödinger eq. of H atom（水素原子のシュレディンガー方程式） convert to the atomic unit（原子単位へ変換する） convert from the xyz to the rθφ(polar) coordinate（xyz座標から極座標へ変換する） separate the variables of ( r, θ, φ) （変数分離する） @ Solution（解） 1 E=-— 2 n 2 ψn, l, m (r, θ, φ) = Rn, l (r) x Yl, m (θ, φ) , Hydrogen-atom wave function Spherical Harmonics （水素原子波動関数） （球面調和関数） Radial wave function （動径波動関数） where Energy （エネルギー） n = 1, 2, 3, . . . l = 0, 1, 2, . . . , n-1 m = 0, ± 1, ± 2, . . . , ±l eliminate a imaginary by linear combination（足し算引き算して虚数を消去する） @ realized Hydrogen-atom wave function （実数化した水素原子波動関数） real ± ψn, l, m (r, θ, φ) = Rn, l (r) x Yl, m (θ, φ) where Realized Spherical Harmonics （実数化した球面調和関数） n = 1, 2, 3, . . . l = 0, 1, 2, . . . , n-1 m = 0, 1, 2, . . . , l

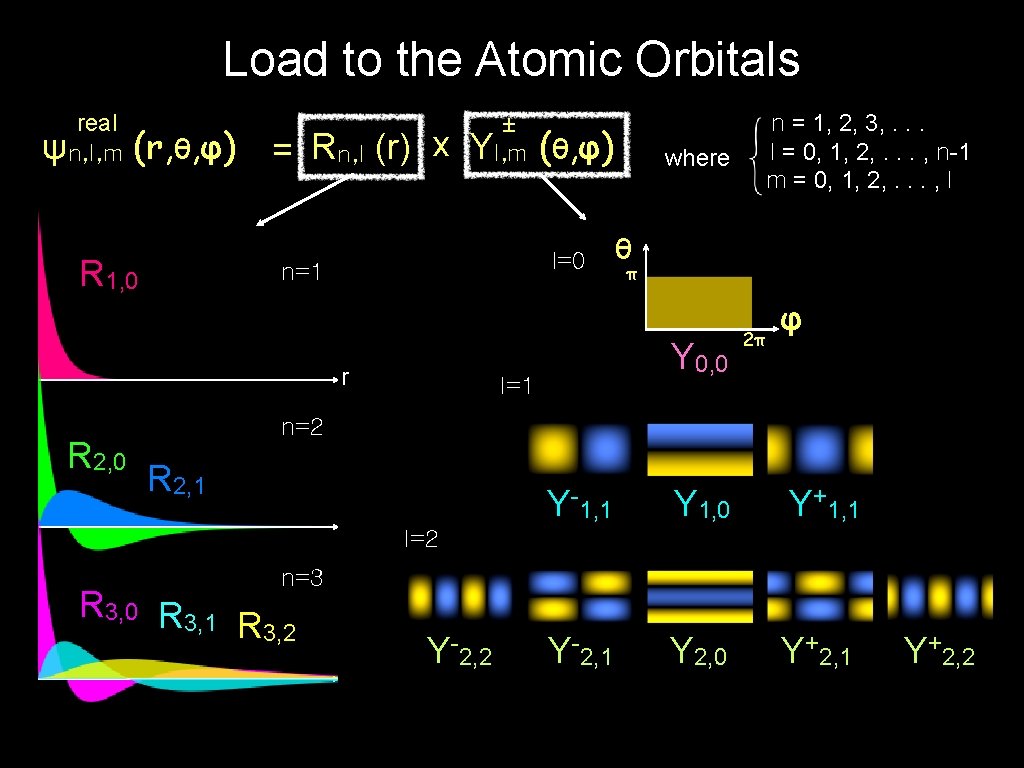
Load to the Atomic Orbitals real ψn, l, m (r, θ, φ) = Rn, l (r) x R 1, 0 ± Yl, m l=0 n=1 r R 2, 0 (θ, φ) where θ π Y 0, 0 l=1 n = 1, 2, 3, . . . l = 0, 1, 2, . . . , n-1 m = 0, 1, 2, . . . , l 2π φ n=2 R 2, 1 Y-1, 1 Y 1, 0 Y+1, 1 Y-2, 1 Y 2, 0 Y+2, 1 l=2 n=3 R 3, 0 R 3, 1 R 3, 2 Y-2, 2 Y+2, 2

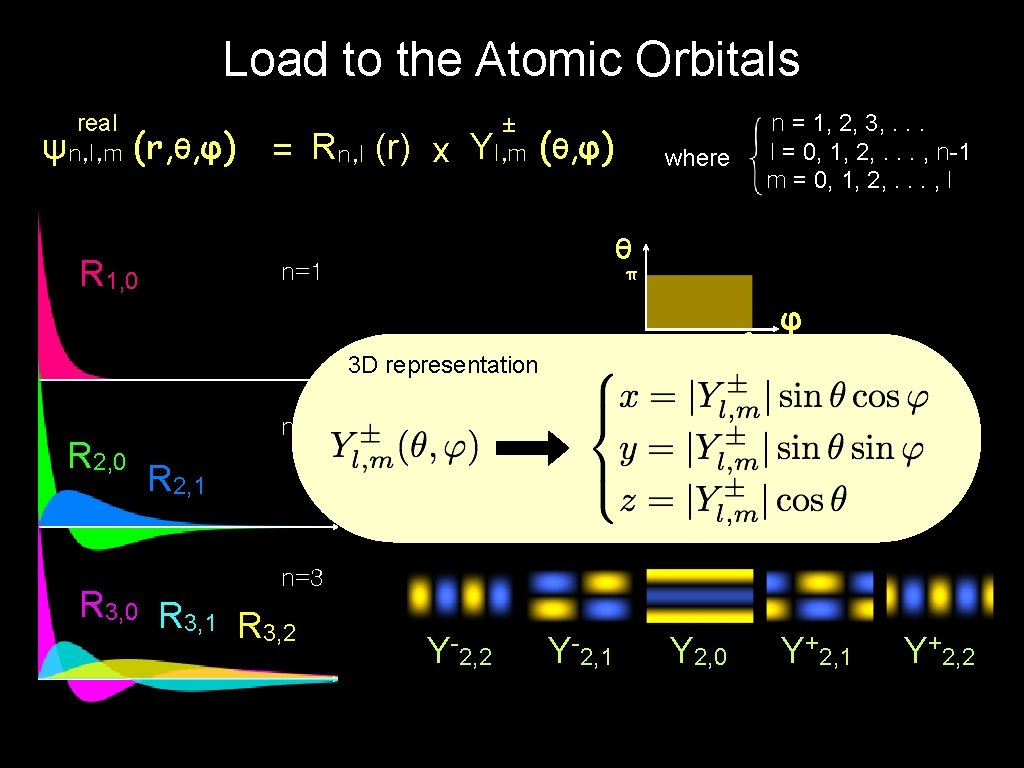
Load to the Atomic Orbitals real ψn, l, m (r, θ, φ) = Rn, l (r) x R 1, 0 ± Yl, m (θ, φ) where θ n=1 π Y 0, 0 3 D representation r R 2, 0 n = 1, 2, 3, . . . l = 0, 1, 2, . . . , n-1 m = 0, 1, 2, . . . , l 2π φ n=2 R 2, 1 Y-1, 1 Y 1, 0 Y+1, 1 Y-2, 1 Y 2, 0 Y+2, 1 n=3 R 3, 0 R 3, 1 R 3, 2 Y-2, 2 Y+2, 2

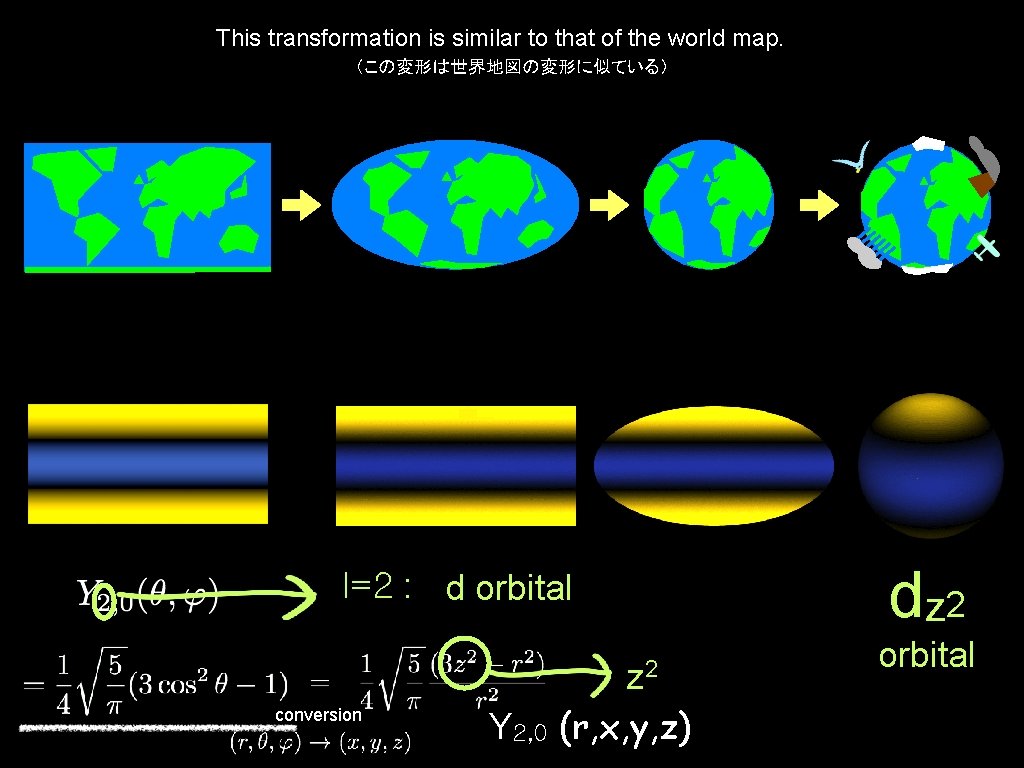
This transformation is similar to that of the world map. （この変形は世界地図の変形に似ている） dz 2 l=2 : d orbital z 2 conversion Y 2, 0 (r, x, y, z) orbital

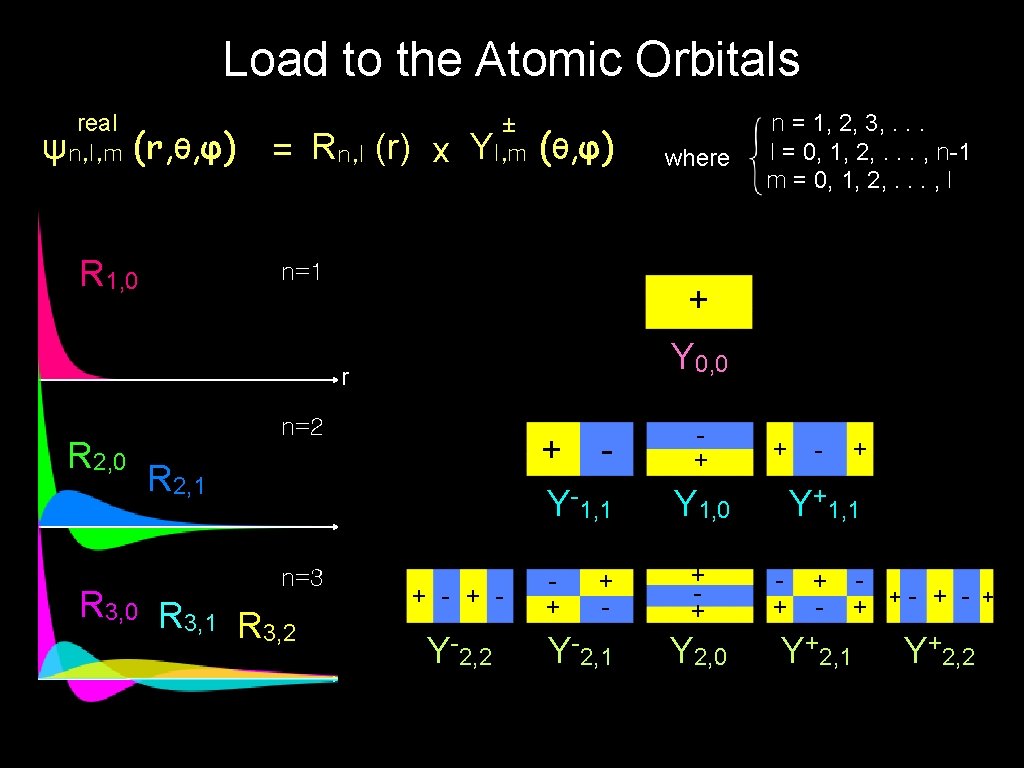
Load to the Atomic Orbitals real ψn, l, m (r, θ, φ) = Rn, l (r) x R 1, 0 ± Yl, m (θ, φ) n=1 + Y 0, 0 r R 2, 0 n=2 + Y-1, 1 R 2, 1 n=3 R 3, 0 R 3, 1 R 3, 2 where n = 1, 2, 3, . . . l = 0, 1, 2, . . . , n-1 m = 0, 1, 2, . . . , l + - Y-2, 2 + + - Y-2, 1 + + Y 2, 0 + Y+1, 1 Y 1, 0 + + - + Y+2, 1 + - Y+2, 2 +

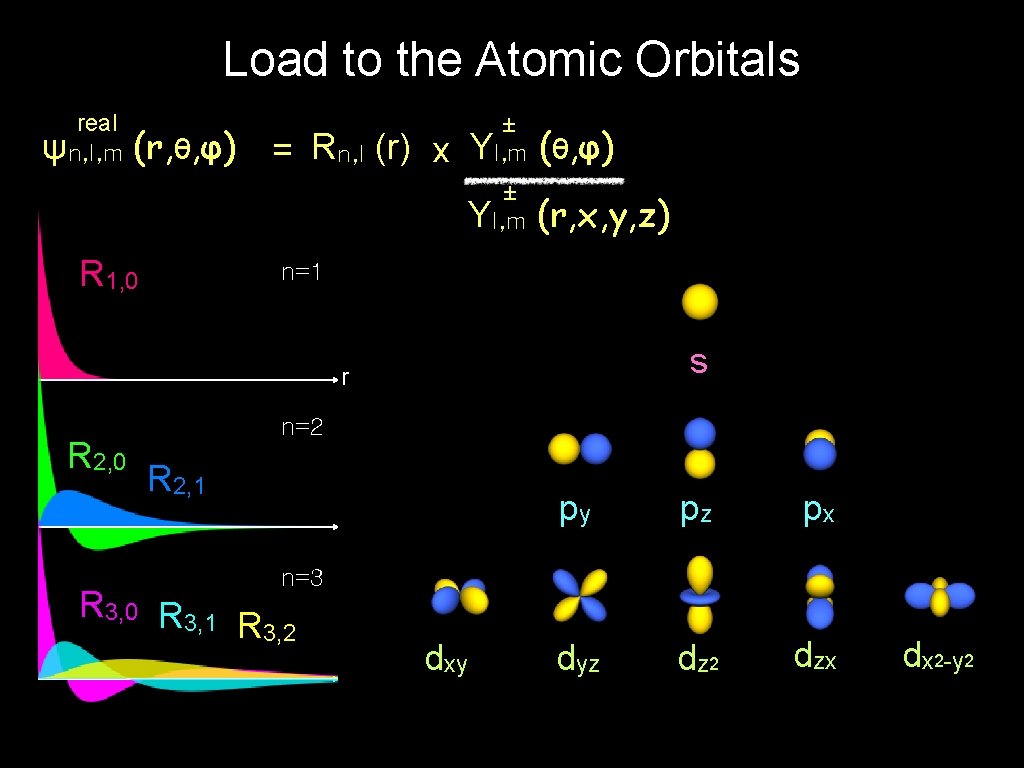
Load to the Atomic Orbitals real ψn, l, m (r, θ, φ) = Rn, l (r) x R 1, 0 ± Yl, m (θ, φ) ± Yl, m (r, x, y, z) n=1 s r R 2, 0 n=2 R 2, 1 py pz px dyz dz 2 dzx n=3 R 3, 0 R 3, 1 R 3, 2 dxy dx 2 -y 2

s orbital Rn, l (r) R 1, 0 x ± Yl, m (r, x, y, z) = real ψn, l, m (r, x, y, z) n=1 1 s R 2, 0 n=2 x s = 2 s n=3 R 3, 0 3 s

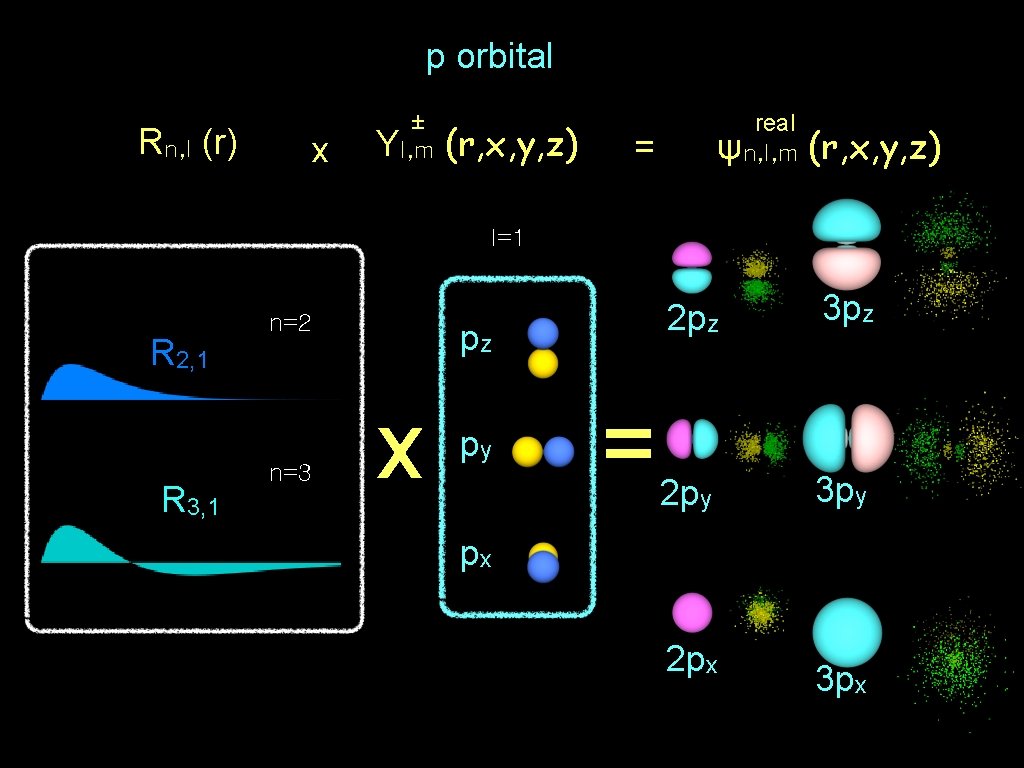
p orbital Rn, l (r) x ± Yl, m (r, x, y, z) real ψn, l, m = (r, x, y, z) l=1 R 2, 1 R 3, 1 n=2 n=3 pz x py = 2 pz 3 pz 2 py 3 py px 2 px 3 px

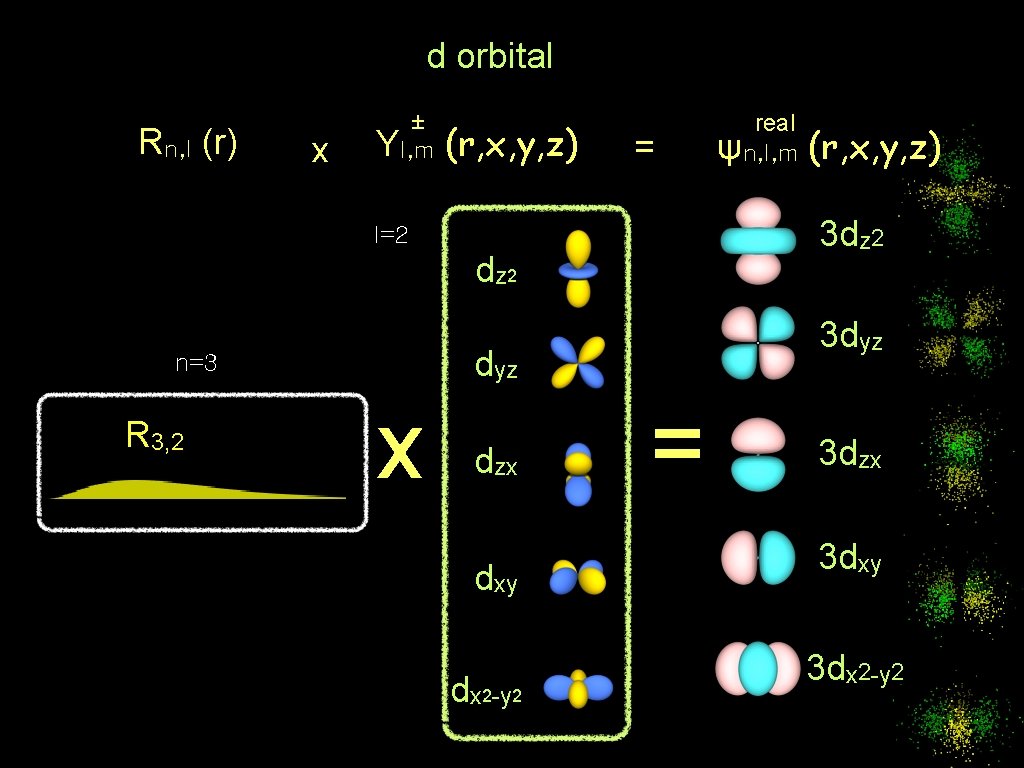
d orbital Rn, l (r) x ± Yl, m (r, x, y, z) = dz 2 R 3, 2 3 dyz x dzx dxy dx 2 -y 2 (r, x, y, z) 3 dz 2 l=2 n=3 real ψn, l, m = 3 dzx 3 dxy 3 dx 2 -y 2

Atomic Orbitals and Energies of the Hydrogen Atom （水素原子の原子軌道とエネルギー）

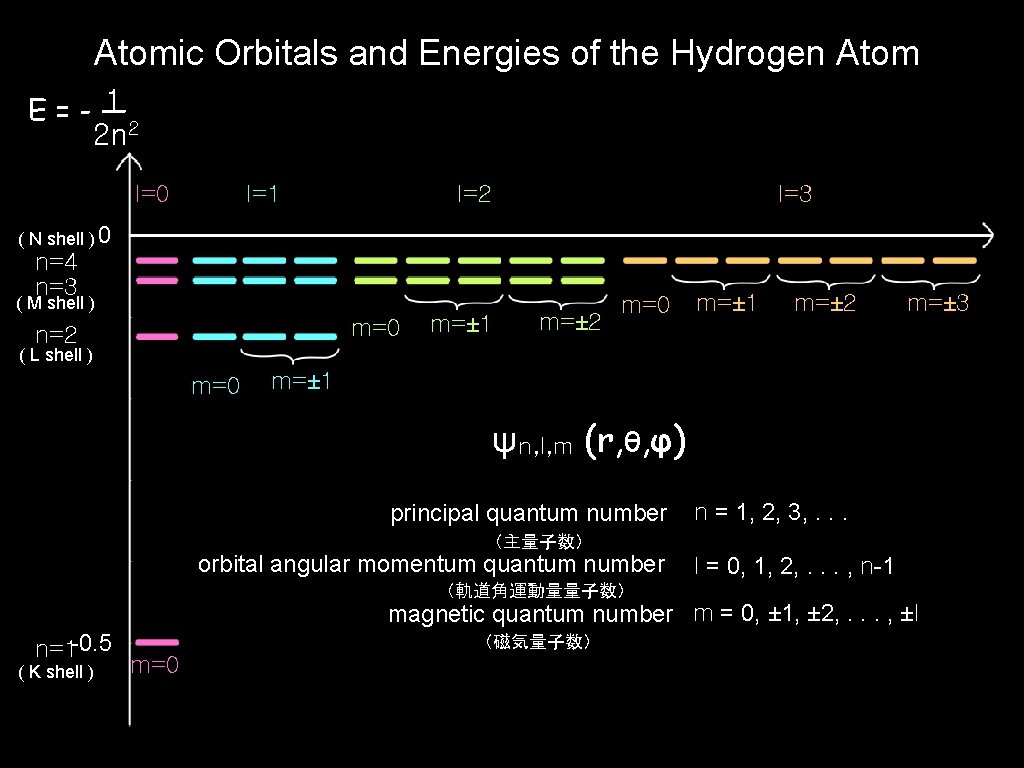
Atomic Orbitals and Energies of the Hydrogen Atom 1 E=-— 2 n 2 l=0 l=1 l=2 l=3 ( N shell ) 0 n=4 n=3 ( M shell ) m=0 n=2 m=± 1 m=± 2 m=0 m=± 1 m=± 2 m=± 3 ( L shell ) m=0 m=± 1 ψn, l, m (r, θ, φ) principal quantum number n = 1, 2, 3, . . . （主量子数） orbital angular momentum quantum number （軌道角運動量量子数） l = 0, 1, 2, . . . , n-1 magnetic quantum number m = 0, ± 1, ± 2, . . . , ±l n=1 -0. 5 ( K shell ) （磁気量子数） m=0

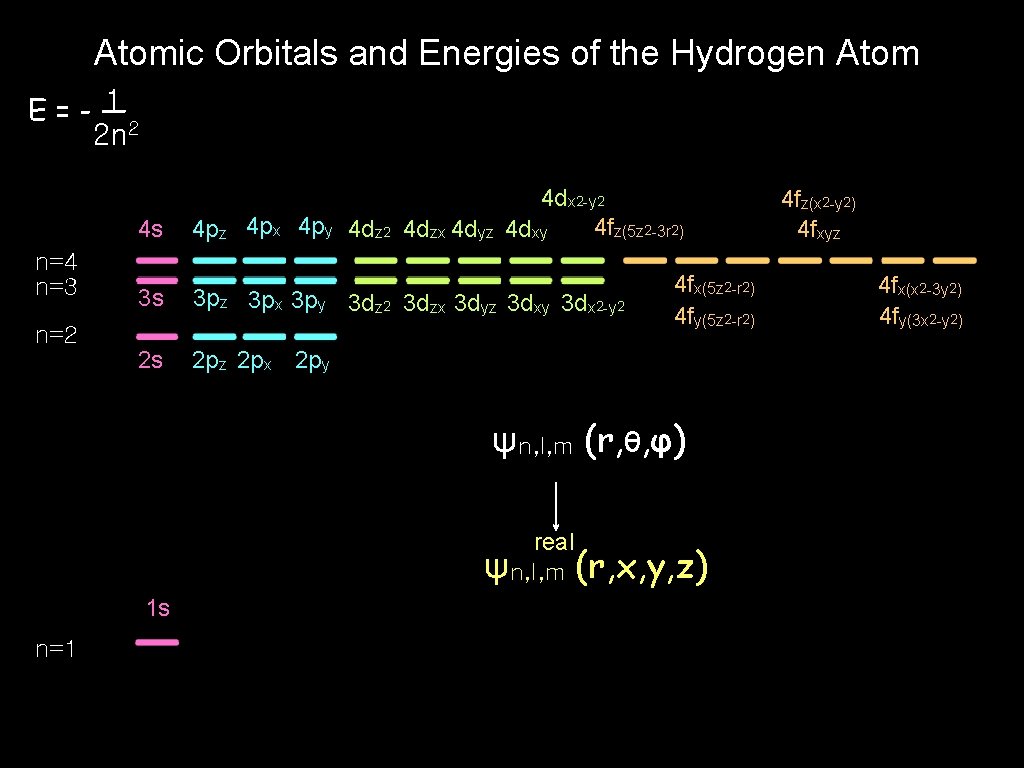
Atomic Orbitals and Energies of the Hydrogen Atom 1 E=-— 2 n 2 n=4 n=3 4 dx 2 -y 2 4 fz(5 z 2 -3 r 2) 4 dxy 4 s 4 pz 4 px 4 py 4 dz 2 4 dzx 4 dyz 3 s 3 pz 3 px 3 py 3 dz 2 3 dzx 3 dyz 3 dxy 3 dx 2 -y 2 2 s 2 pz 2 px 2 py n=2 4 fx(5 z 2 -r 2) 4 fy(5 z 2 -r 2) ψn, l, m (r, θ, φ) real ψn, l, m (r, x, y, z) 1 s n=1 4 fz(x 2 -y 2) 4 fxyz 4 fx(x 2 -3 y 2) 4 fy(3 x 2 -y 2)

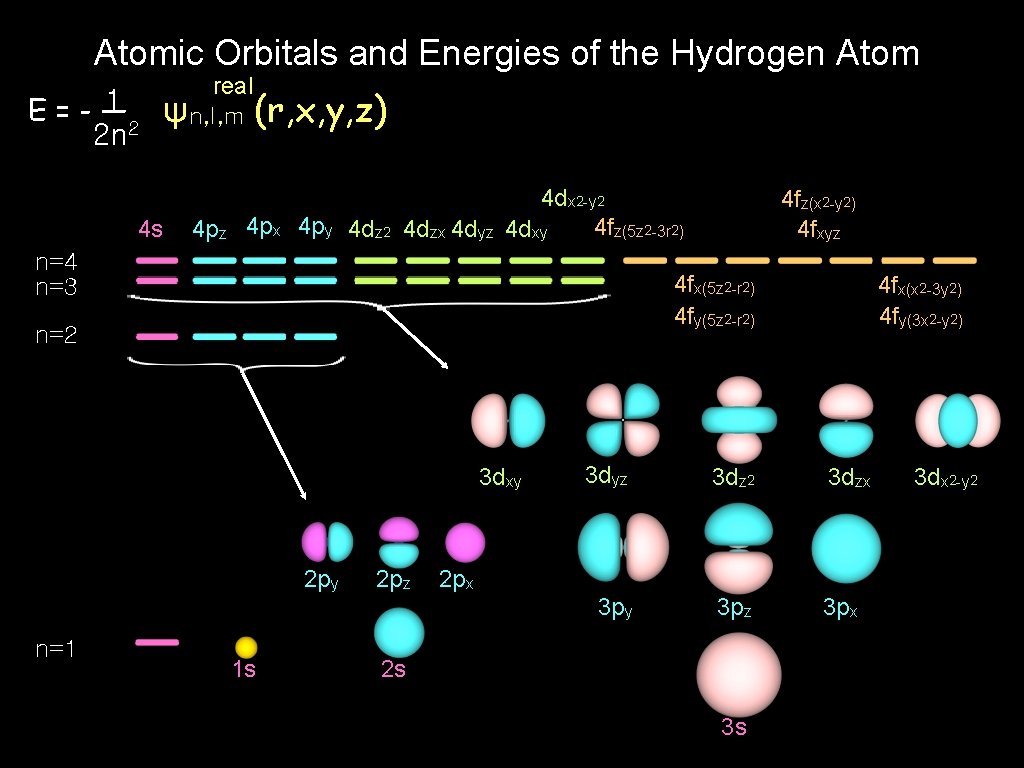
Atomic Orbitals and Energies of the Hydrogen Atom 1 E=-— 2 n 2 real ψn, l, m (r, x, y, z) 4 s 4 pz 4 px 4 py 4 dz 2 4 dzx 4 dyz 4 dx 2 -y 2 4 fz(5 z 2 -3 r 2) 4 dxy n=4 n=3 4 fx(5 z 2 -r 2) 4 fy(5 z 2 -r 2) n=2 3 dxy 2 py n=1 4 fz(x 2 -y 2) 4 fxyz 1 s 2 pz 4 fx(x 2 -3 y 2) 4 fy(3 x 2 -y 2) 3 dyz 3 dz 2 3 dzx 3 py 3 pz 3 px 2 s 3 s 3 dx 2 -y 2

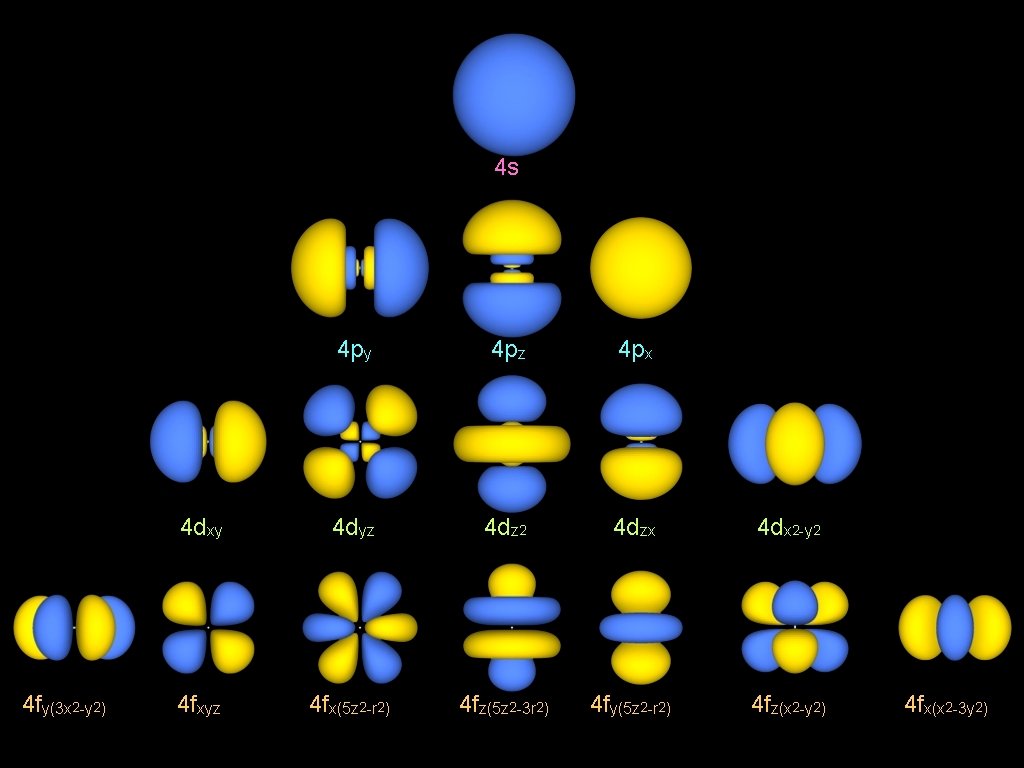
4 s 4 fy(3 x 2 -y 2) 4 py 4 pz 4 px 4 dxy 4 dyz 4 dz 2 4 dzx 4 dx 2 -y 2 4 fxyz 4 fx(5 z 2 -r 2) 4 fz(5 z 2 -3 r 2) 4 fy(5 z 2 -r 2) 4 fz(x 2 -y 2) 4 fx(x 2 -3 y 2)

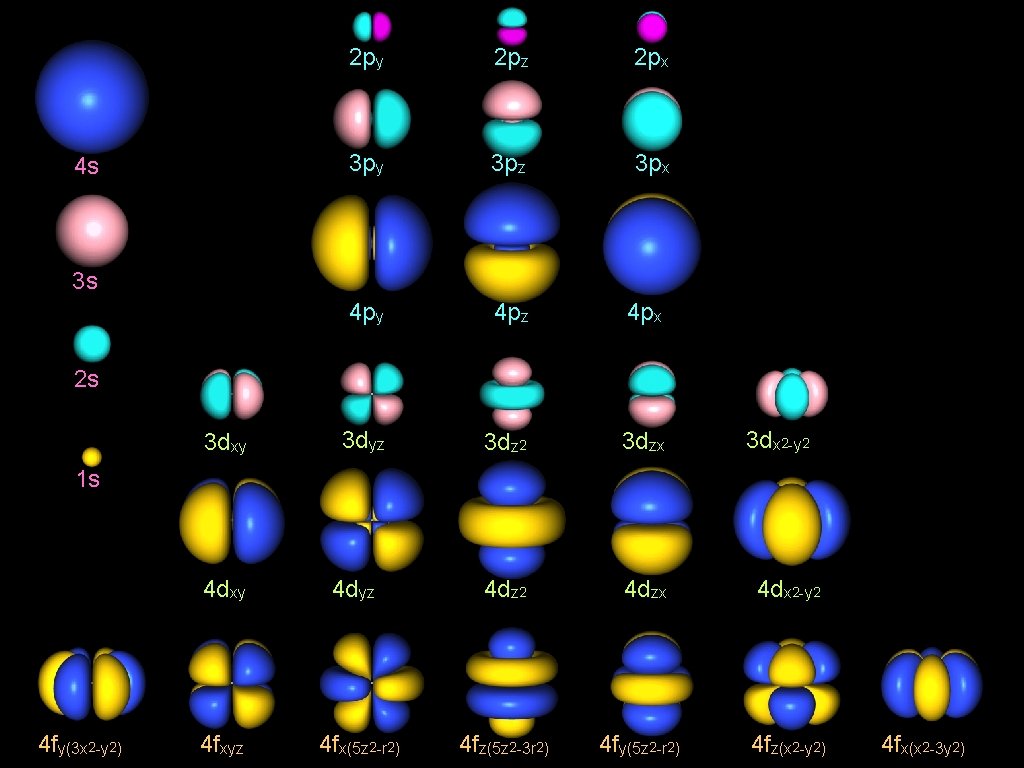
4 s 2 py 2 pz 2 px 3 py 3 pz 3 px 4 py 4 pz 4 px 3 dyz 3 dz 2 3 dzx 3 s 2 s 3 dxy 3 dx 2 -y 2 1 s 4 fy(3 x 2 -y 2) 4 dxy 4 dyz 4 dz 2 4 dzx 4 dx 2 -y 2 4 fxyz 4 fx(5 z 2 -r 2) 4 fz(5 z 2 -3 r 2) 4 fy(5 z 2 -r 2) 4 fz(x 2 -y 2) 4 fx(x 2 -3 y 2)