Atomic Molecular Clusters 5 Metal Clusters Metal clusters

Atomic & Molecular Clusters 5. Metal Clusters • Metal clusters have been widely studied – especially alkali metals, noble metals (Cu, Ag, Au) and transition metals. • Cohesive energies are generally quite large (relatively strong metallic bonding) – significantly higher than for rare gas or molecular clusters – so they may be studied in solution (colloidal suspensions), on surfaces or in inert matrices, as well as in the gas phase. • A number of models have been introduced to explain and predict the properties of metal clusters.

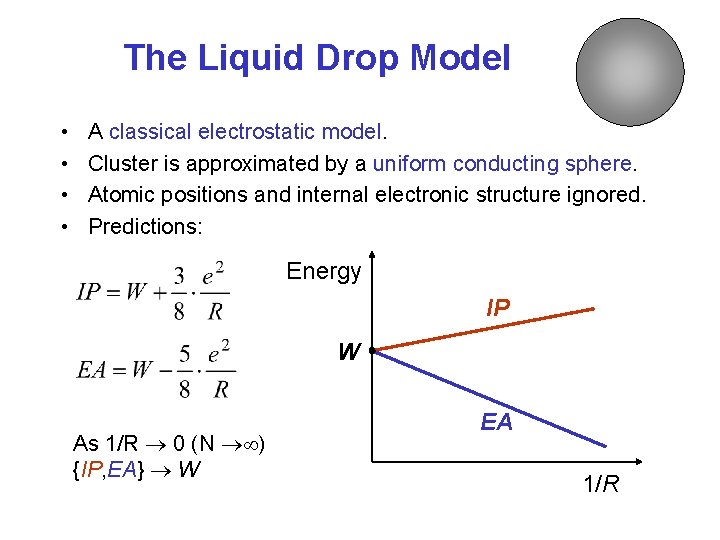
The Liquid Drop Model • • A classical electrostatic model. Cluster is approximated by a uniform conducting sphere. Atomic positions and internal electronic structure ignored. Predictions: Energy IP W As 1/R 0 (N ) {IP, EA} W EA 1/R

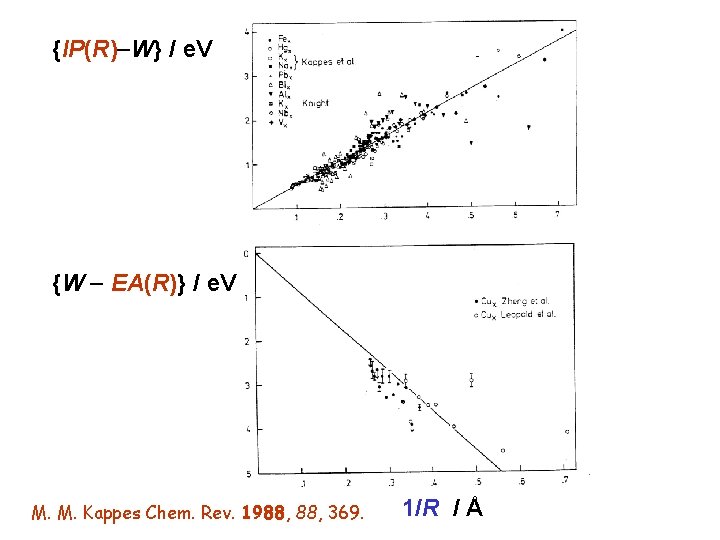
{IP(R) W} / e. V {W EA(R)} / e. V M. M. Kappes Chem. Rev. 1988, 369. 1/R / Å

Failures of the Liquid Drop Model • Deviations from 1/R dependence of IPs and EAs for small clusters. • IPs of Hg clusters show a discontinuity due to a sizedependent non-metal transition (see later). • Some transition metals (where ionization involves removal of tightly bound d electrons, e. g. Fe, Ni) show small variation of IP/EA with size. • Magnetic effects (spin-spin interactions) also important for transition metals. • LDM does not reproduce fine structure in IP/EA variation with N (e. g. “even-odd alternation”) or explain the Magic Numbers in the mass spectra. • Require a Quantum Mechanical model with discrete electronic states JELLIUM MODEL.

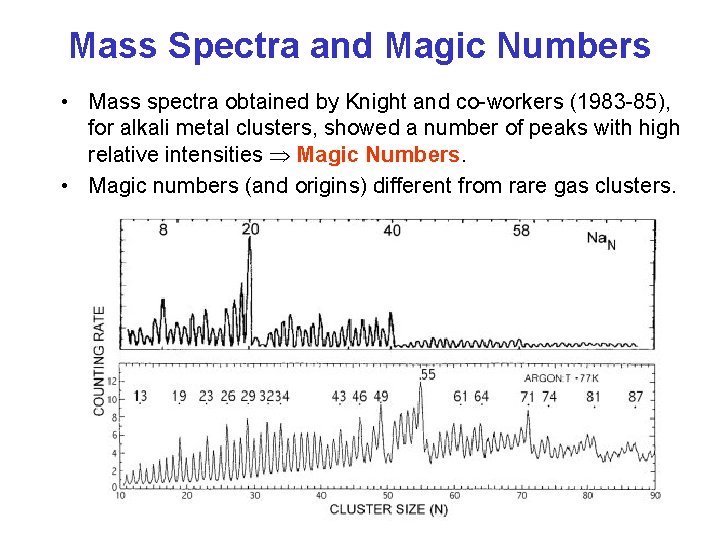
Mass Spectra and Magic Numbers • Mass spectra obtained by Knight and co-workers (1983 -85), for alkali metal clusters, showed a number of peaks with high relative intensities Magic Numbers. • Magic numbers (and origins) different from rare gas clusters.

The Jellium Model • Derived from nuclear structure theory. • Cluster approximated by a sphere with a uniform positively charged background, filled with an “electron gas” (valence electrons). • Valence electrons are delocalized – move in a smooth, attractive, central, mean field potential of spherical symmetry.

• Positions of ionic cores are ignored. • This is justified if: – electrons are strongly delocalized – ionic background easily deformed – molten clusters? • Works best for monovalent simple metals – e. g. alkali metals, noble metals (Cu, Ag, Au). • Unlike the LDM, the jellium model is a quantum mechanical model – quantization of electron energy levels due to boundary conditions imposed by the potential. • Gives rise to electronic shell structure for metal clusters with up to several 1000 s of atoms.

Empirical Jellium Models • Based on effective single-particle potentials (Knight, Clemenger). • Solve 1 -electron Schrödinger Equation for an electron in a sphere, under the influence of an attractive central potential. • Wavefunction ( ) is separable into radial and angular parts: n, , m (r, , ) = Rn, (r). Y , m ( , )

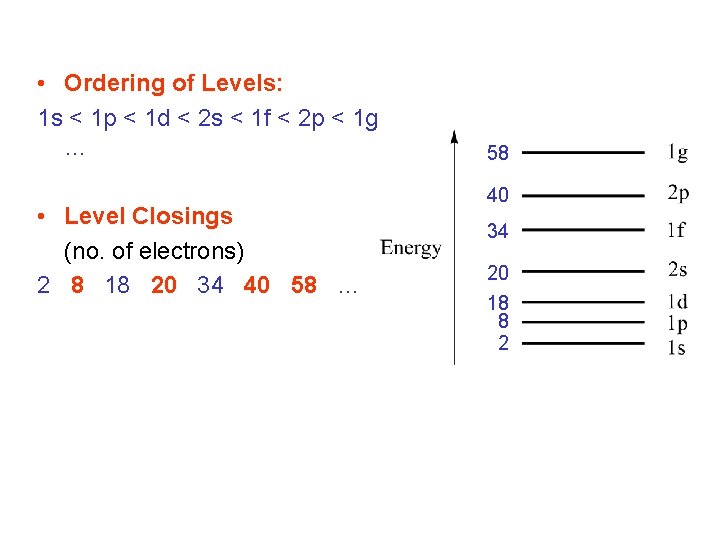
Solutions • Wavefunction and energies depend on quantum numbers: n = 1, 2, 3, … = 0, 1, 2, … m = … 0 … + (no restriction on ) (2 + 1)-degenerate • Note: the principal quantum number n is different from that used for atomic orbitals (follows convention of nuclear physics): nclust = natom - • Jellium electronic levels (sets of degenerate orbitals) are labelled, by analogy with atomic orbitals: 1 s, 1 p, …, 2 s, 2 p … • Exact ordering of orbitals depends on the radial form of the potential.

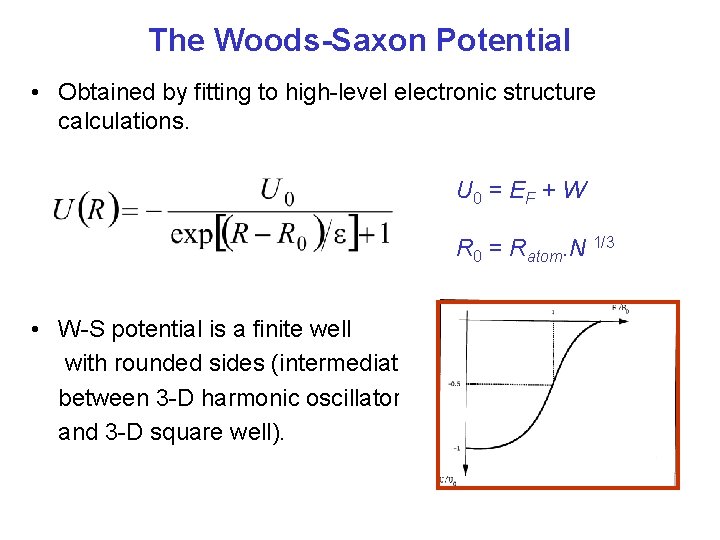
The Woods-Saxon Potential • Obtained by fitting to high-level electronic structure calculations. U 0 = E F + W R 0 = Ratom. N 1/3 • W-S potential is a finite well with rounded sides (intermediate between 3 -D harmonic oscillator and 3 -D square well).

• Ordering of Levels: 1 s < 1 p < 1 d < 2 s < 1 f < 2 p < 1 g … • Level Closings (no. of electrons) 2 8 18 20 34 40 58 … 58 40 34 20 18 8 2

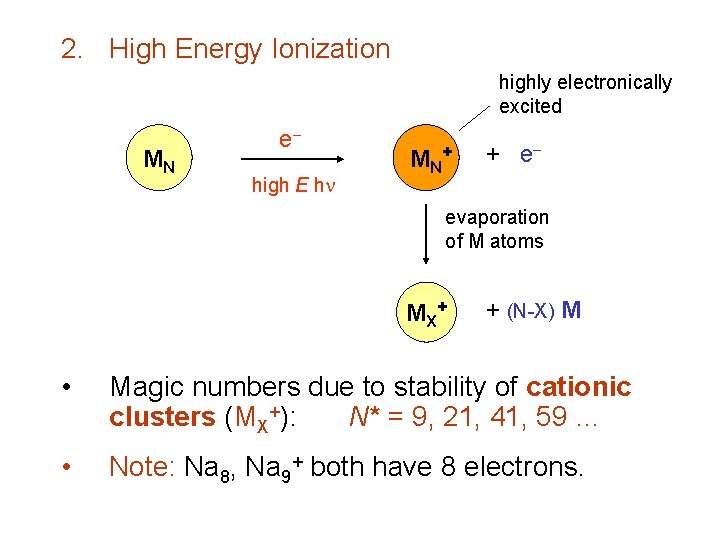
Interpreting Mass Spectra of Metal Clusters 1. Low Energy Ionization MN h MN + + e • Magic numbers (intense peaks in MS) due to stable electron counts (filled jellium levels) of neutral clusters (MN). • N* = 8, 20, 40, 58 …

2. High Energy Ionization highly electronically excited MN e high E h MN + + e evaporation of M atoms MX + + (N-X) M • Magic numbers due to stability of cationic clusters (MX+): N* = 9, 21, 41, 59 … • Note: Na 8, Na 9+ both have 8 electrons.

Breakdown of the Spherical Jellium Model • Fine structure is observed in the MS, IPs, EAs, polarizabilities etc. , for even-electron counts other than those predicted by the (spherical) jellium model. • This is evidence for non-degenerate electronic sub-levels, which cannot be explained by the spherical jellium model. • Need to extend the model.

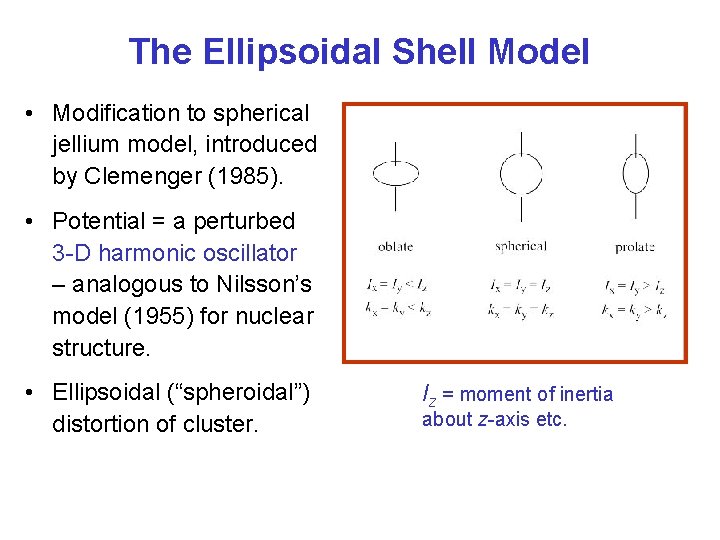
The Ellipsoidal Shell Model • Modification to spherical jellium model, introduced by Clemenger (1985). • Potential = a perturbed 3 -D harmonic oscillator – analogous to Nilsson’s model (1955) for nuclear structure. • Ellipsoidal (“spheroidal”) distortion of cluster. Iz = moment of inertia about z-axis etc.

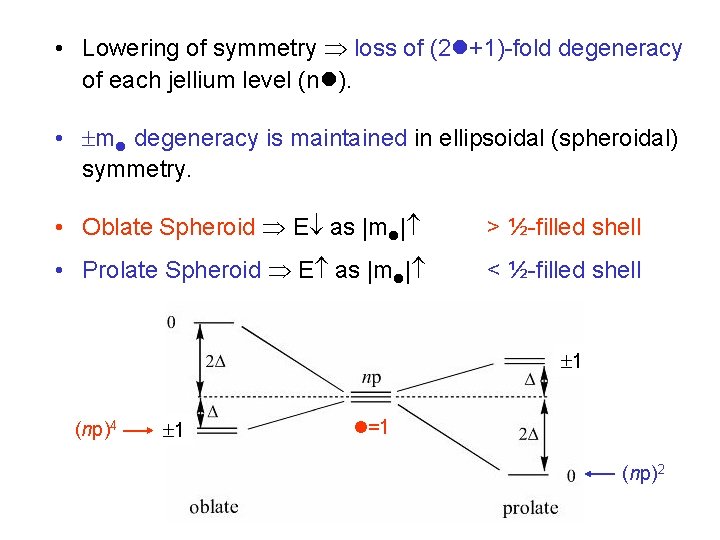
• Lowering of symmetry loss of (2 +1)-fold degeneracy of each jellium level (n ). • m degeneracy is maintained in ellipsoidal (spheroidal) symmetry. • Oblate Spheroid E as |m | > ½-filled shell • Prolate Spheroid E as |m | < ½-filled shell 1 (np)4 1 =1 (np)2

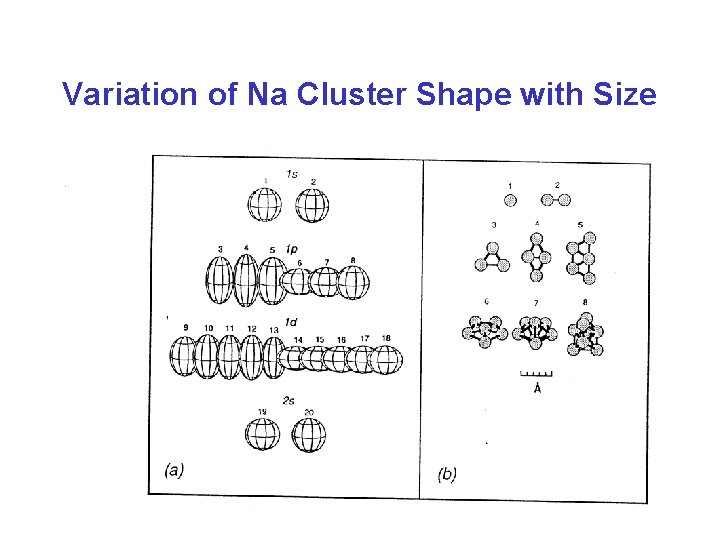
Variation of Na Cluster Shape with Size

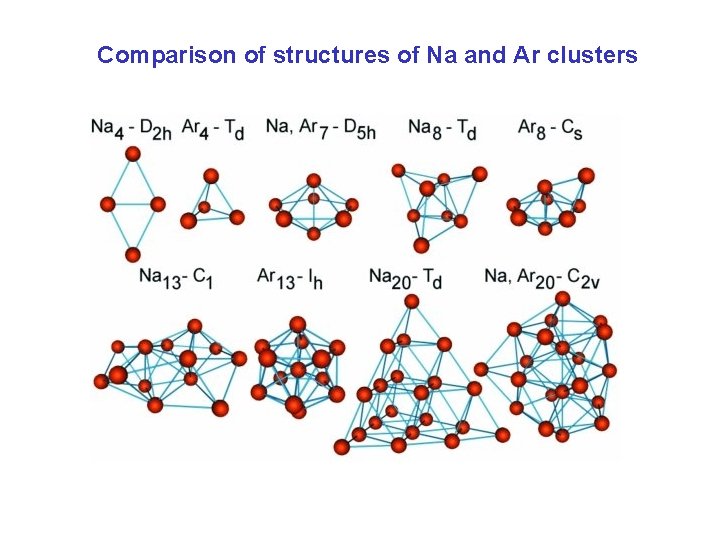
Comparison of structures of Na and Ar clusters

Beyond the Jellium Model • Martin and co-workers (1991)* measured MS of Na. N clusters (N 25, 000). • Observed two series of periodic intensity variations: period N 1/3 * T. P. Martin et al. , J. Phys. Chem. 1991, 95, 6421.

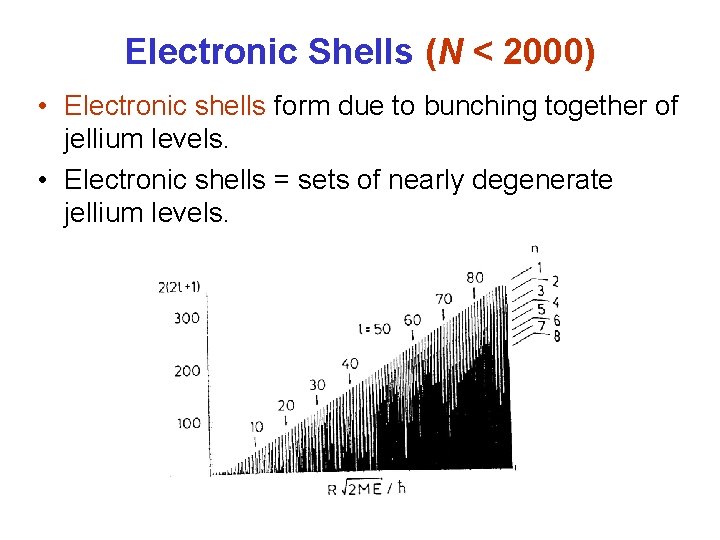
Electronic Shells (N < 2000) • Electronic shells form due to bunching together of jellium levels. • Electronic shells = sets of nearly degenerate jellium levels.

• For larger metal clusters, electronic effects are relatively unimportant because electronic shells merge to form quasi-continuous bands (bulk-like band structure). jellium levels N electronic shells band structure

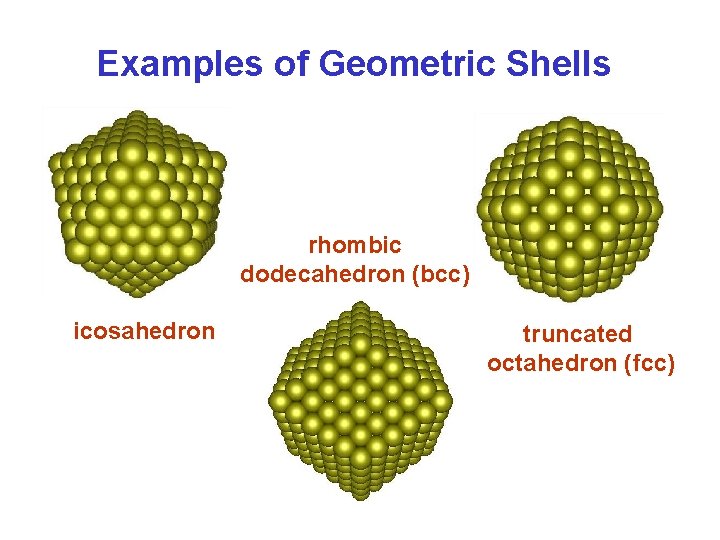
Geometric Shells (N > 2000) • Geometric shells correspond to complete concentric polyhedral shells of atoms – as for rare gas clusters. • Stability due to minimization of surface energy. • Alkali Metal Clusters – magic numbers are consistent with filling K geometric shells:

Examples of Geometric Shells rhombic dodecahedron (bcc) icosahedron truncated octahedron (fcc)

• Similar magic numbers have been observed for Ca clusters with up to 5000 atoms. * Ca. N+ N • MS magic numbers and fine structure (due to partial geometric shell formation) indicate that alkali metal clusters (with N > 2000) and Ca clusters have icosahedral shell structure. * T. P. Martin Physics Reports 1996, 273, 199.

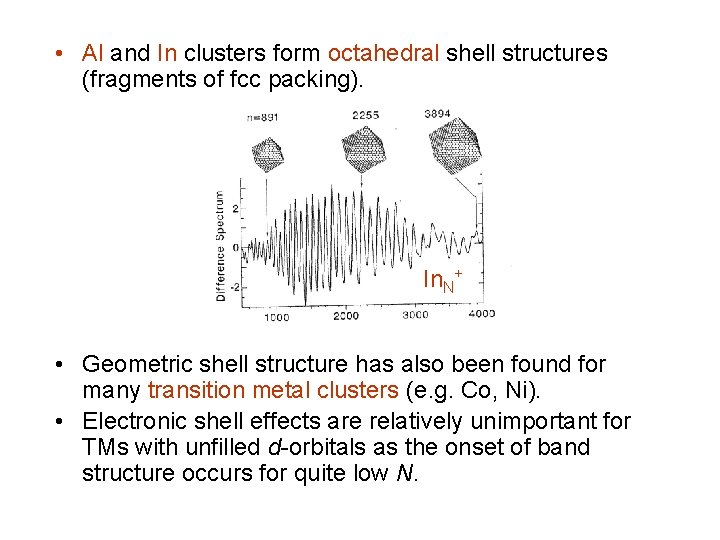
• Al and In clusters form octahedral shell structures (fragments of fcc packing). In. N+ • Geometric shell structure has also been found for many transition metal clusters (e. g. Co, Ni). • Electronic shell effects are relatively unimportant for TMs with unfilled d-orbitals as the onset of band structure occurs for quite low N.

Microscopy Studies of Metal Clusters • A number of microscopy techniques can be applied to study metal clusters: – Electron Microscopy (TEM, SEM) – Scanning Tunnelling Microscopy (STM) – Atomic Force Microscopy (AFM) • Clusters must be immobilized on a substrate (e. g. graphite, amorphous-C, Mg. O, Si. O 2 – depending on the type of measurement). • Clusters are often passivated by surfactant (ligand) molecules. • Cluster-surface and cluster-ligand interaction may affect cluster structure (for small clusters).

Electron Micrographs of Ag and Au Particles 15 nm 4 nm Single Ag decahedron Multiply-twinned Ag fcc particle 3 nm 7 nm Intergrowth of 2 Au icosahedra Truncated octahedral Au fcc particle Marks decahedral Au particle

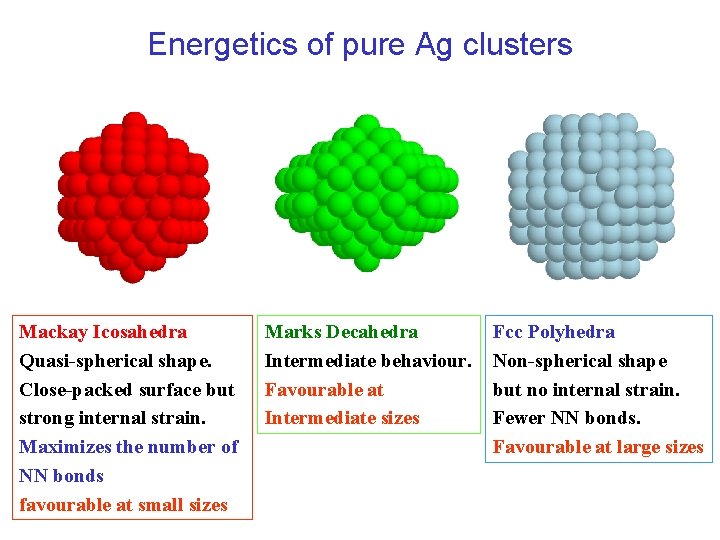
Energetics of pure Ag clusters Mackay Icosahedra Quasi-spherical shape. Close-packed surface but strong internal strain. Maximizes the number of NN bonds favourable at small sizes Marks Decahedra Intermediate behaviour. Favourable at Intermediate sizes Fcc Polyhedra Non-spherical shape but no internal strain. Fewer NN bonds. Favourable at large sizes

Insulator-Metal Transition in Hg Clusters • Rademann and Hensel (1987) measured IPs of Hg clusters as a function of size, N. • Explained in terms of a gradual transition: Insulating Semi-Conducting Metallic in the region N ~ 13 -70. • Consistent with spectroscopy and theoretical calculations.

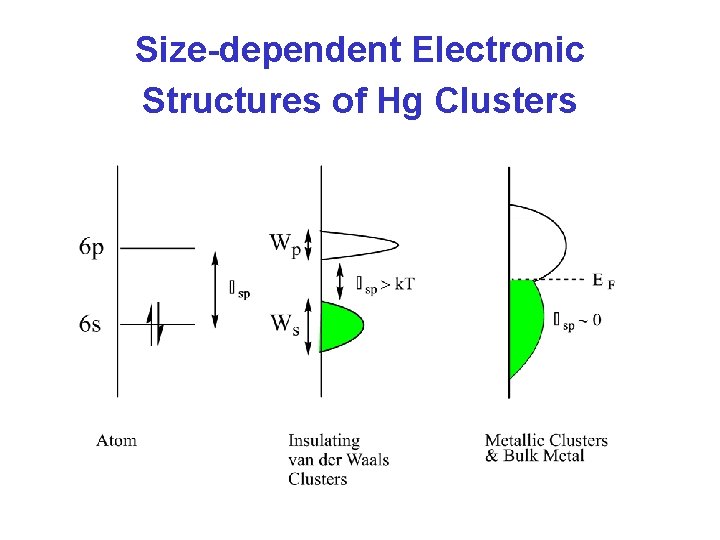
Theory of Bonding in Hg Clusters • The free Hg atom has a closed shell: (6 s)2(6 p)0 – Small clusters are insulating “van der Waals clusters” – held together by dispersion forces. • As the cluster gets larger, the 6 s and 6 p levels broaden into bands (with widths Ws and Wp) – W as N • Insulator Metal Transition occurs when the 6 s and 6 p bands overlap. • Before band overlap (intermediate N), the band gap ( sp) may be comparable to thermal energy (k. T) – semi-conductor clusters – s-p hybridization occurs covalent bonding

Size-dependent Electronic Structures of Hg Clusters