Atmospheric Water Global energy balance Atmospheric circulation Atmospheric

Atmospheric Water • Global energy balance • Atmospheric circulation • Atmospheric water vapor • Reading: Sections 3. 1 and 3. 2 for today, 3. 3 and 3. 4 for next Tues • Also, please read article by Morel from Gewex News, Vol. 17 No. 4, Nov 2007

Atmospheric Water • Global energy balance • Atmospheric circulation • Atmospheric water vapor

Radiation • Two basic laws – Stefan-Boltzman Law • R = emitted radiation (W/m 2) • e = emissivity (0 -1) • s = 5. 67 x 10 -8 W/m 2 -K 4 • T = absolute temperature (K) All bodies emit radiation – Wiens Law • l = wavelength of emitted radiation (m) Hot bodies (sun) emit short wave radiation Cool bodies (earth) emit long wave radiation

Net Radiation, Rn Ri Incoming Radiation Re Ro =a. Ri Reflected radiation a= albedo (0 – 1) Rn Net Radiation Average value of Rn over the earth and over the year is 105 W/m 2

Net Radiation, Rn H – Sensible Heat LE – Evaporation G – Ground Heat Flux Rn Net Radiation Average value of Rn over the earth and over the year is 105 W/m 2

Energy Balance of Earth 6 70 20 100 6 26 4 38 15 19 21 51 Sensible heat flux 7 Latent heat flux 23 http: //www. uwsp. edu/geo/faculty/ritter/geog 101/textbook/energy/radiation_balance. html

Diurnal Variation Downward shortwave July 2003 San Marcos Basin Upward Longwave Downward longwave Diurnal variation of fluxes, Upward shortwave Ground Fluxes in W/m 2 Latent Sensible

Energy Balance in the San Marcos Basin from the NARR (July 2003) Note the very large amount of longwave radiation exchanged between land atmosphere Average fluxes over the day 495 61 72 310 Net Shortwave = 310 – 72 = 238; 3 112 415 Net Longwave = 415 – 495 = - 80
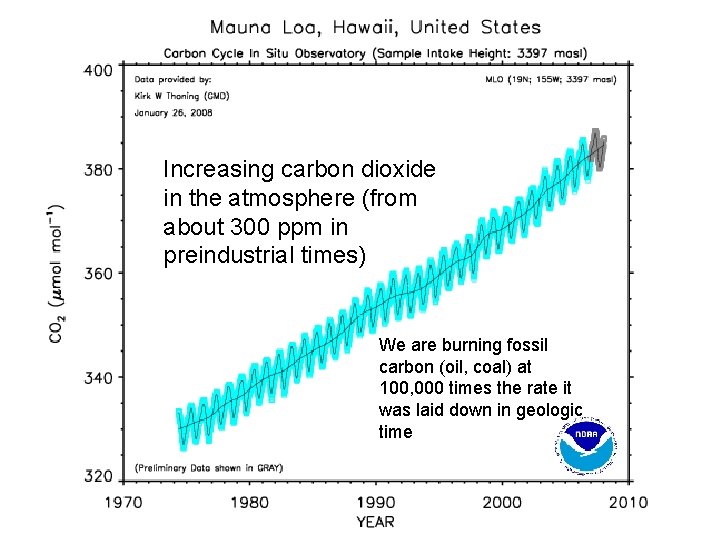
Increasing carbon dioxide in the atmosphere (from about 300 ppm in preindustrial times) We are burning fossil carbon (oil, coal) at 100, 000 times the rate it was laid down in geologic time
Absorption of energy by CO 2

Atmospheric Water • Global energy balance • Atmospheric circulation • Atmospheric water vapor

Heating of earth surface • Heating of earth surface is uneven – Solar radiation strikes perpendicularly near the equator (270 W/m 2) – Solar radiation strikes at an oblique angle near the poles (90 Amount of energy transferred from W/m 2) equator to the poles is • Emitted radiation is approximately 4 x 109 MW more uniform than incoming radiation
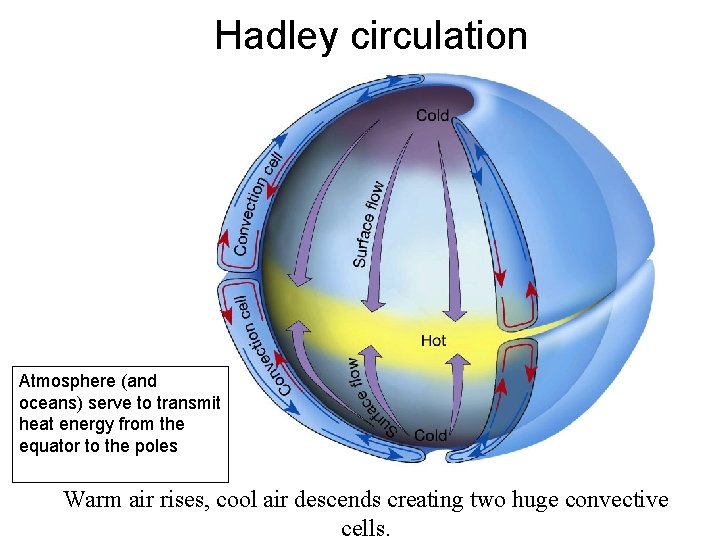
Hadley circulation Atmosphere (and oceans) serve to transmit heat energy from the equator to the poles Warm air rises, cool air descends creating two huge convective cells.

Conservation of Angular Momentum (Coriolis Force) No external forces on air, so m. V 1 r 1 = m. V 2 r 2 m. V 1 r 1 < r 2 so V 1 > V 2 m. V 2 r 2 Intertropical Convergence Zone Earth rotation Near equator, air starts to “fall behind” the earth V 1 Earth rotation r 1 r 2 V 2 Looking down from North Pole, earth is rotating counterclockwise

Atmospheric circulation Circulation cells Polar Cell 1. Hadley cell 2. Ferrel Cell 3. Polar cell Winds 1. Tropical Easterlies/Trades 2. Westerlies 3. Polar easterlies Latitudes 1. Intertropical convergence zone (ITCZ)/Doldrums 2. Horse latitudes 3. Subpolar low 4. Polar high
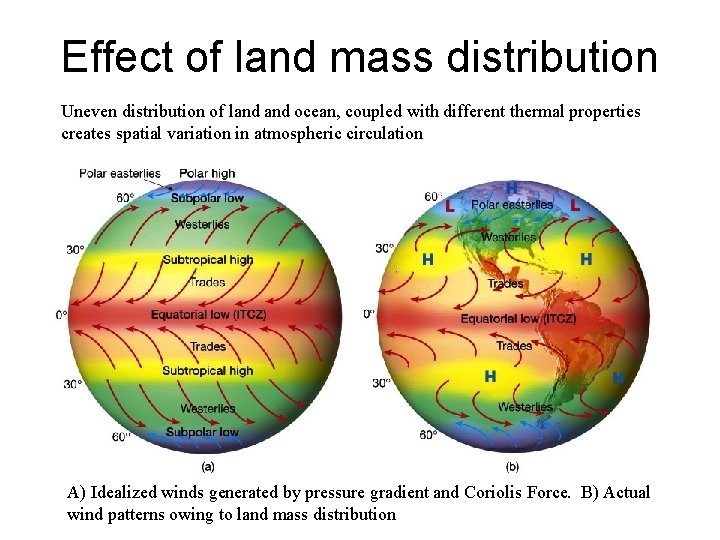
Effect of land mass distribution Uneven distribution of land ocean, coupled with different thermal properties creates spatial variation in atmospheric circulation A) Idealized winds generated by pressure gradient and Coriolis Force. B) Actual wind patterns owing to land mass distribution

Shifting in Intertropical Convergence Zone (ITCZ) Owing to the tilt of the Earth's axis in orbit, the ITCZ shifts north and south. Southward shift in January Creates wet Summers (Monsoons) and dry winters, especially in India and SE Asia Northward shift in July

ITCZ movement http: //iri. ldeo. columbia. edu/%7 Ebgordon/ITCZ. html

Atmospheric Water • Global energy balance • Atmospheric circulation • Atmospheric water vapor

Structure of atmosphere

Atmospheric water • Atmospheric water exists – Mostly as gas or water vapor – Liquid in rainfall and water droplets in clouds – Solid in snowfall and in hail storms • Accounts for less than 1/100, 000 part of total water, but plays a major role in the hydrologic cycle

Water vapor Suppose we have an elementary volume of atmosphere d. V and we want quantify how much water vapor it contains Water vapor density Air density d. V ma = mass of moist air mv = mass of water vapor Atmospheric gases: Nitrogen – 78. 1% Oxygen – 20. 9% Other gases ~ 1% http: //www. bambooweb. com/articles/e/a/Earth's_atmosphere. html

Specific Humidity, qv • Specific humidity measures the mass of water vapor per unit mass of moist air • It is dimensionless

Vapor pressure, e • Vapor pressure, e, is the pressure that water vapor exerts on a surface • Air pressure, p, is the total pressure that air makes on a surface • Ideal gas law relates pressure to absolute temperature T, Rv is the gas constant for water vapor • 0. 622 is ratio of mol. wt. of water vapor to avg mol. wt. of dry air

Dalton’s Law of Partial Pressures John Dalton studied the effect of gases in a mixture. He observed that the Total Pressure of a gas mixture was the sum of the Partial Pressure of each gas. P total = P 1 + P 2 + P 3 +. . . . Pn The Partial Pressure is defined as the pressure of a single gas in the mixture as if that gas alone occupied the container. In other words, Dalton maintained that since there was an enormous amount of space between the gas molecules within the mixture that the gas molecules did not have any influence on the motion of other gas molecules, therefore the pressure of a gas sample would be the same whether it was the only gas in the container or if it were among other gases. http: //members. aol. com/profchm/dalton. html

Avogadro’s law Equal volumes of gases at the same temperature and pressure contain the same number of molecules regardless of their chemical nature and physical properties. This number (Avogadro's number) is 6. 023 X 1023 in 22. 41 L for all gases. Dry air ( z = x+y molecules) Moist air (x dry and y water vapor) Dry air Water vapor rd = (x+y) * Md/Volume rm = (x* Md + y*Mv)/Volume rm < rd, which means moist air is lighter than dry air!

Saturation vapor pressure, es Saturation vapor pressure occurs when air is holding all the water vapor that it can at a given air temperature Vapor pressure is measured in Pascals (Pa), where 1 Pa = 1 N/m 2 1 k. Pa = 1000 Pa

Relative humidity, Rh es e Relative humidity measures the percent of the saturation water content of the air that it currently holds (0 – 100%)
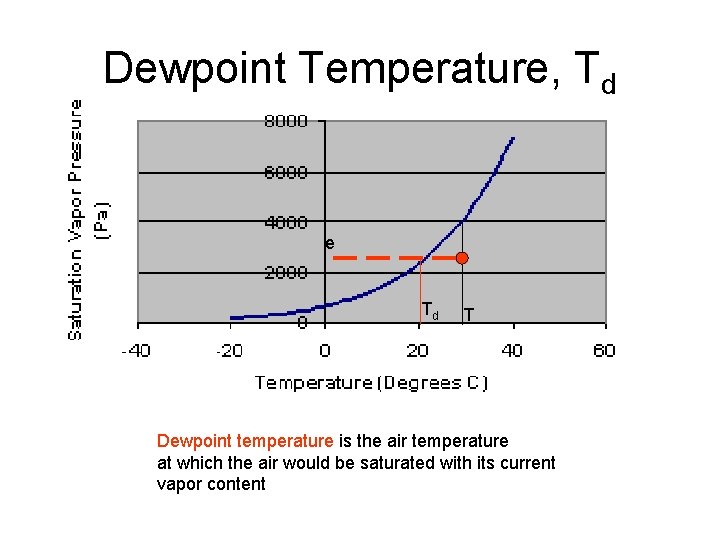
Dewpoint Temperature, Td e Td T Dewpoint temperature is the air temperature at which the air would be saturated with its current vapor content

Water vapor in an air column • We have three equations describing column: 2 – Hydrostatic air pressure, dp/dz = -rag – Lapse rate of temperature, d. T/dz = - a – Ideal gas law, p = ra. Ra. T • Combine them and integrate over column to get pressure variation elevation Column Element, dz 1
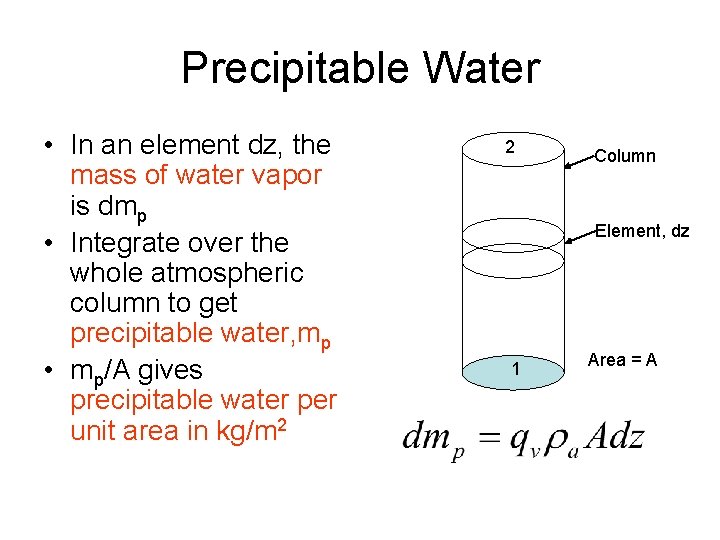
Precipitable Water • In an element dz, the mass of water vapor is dmp • Integrate over the whole atmospheric column to get precipitable water, mp • mp/A gives precipitable water per unit area in kg/m 2 2 Column Element, dz 1 Area = A
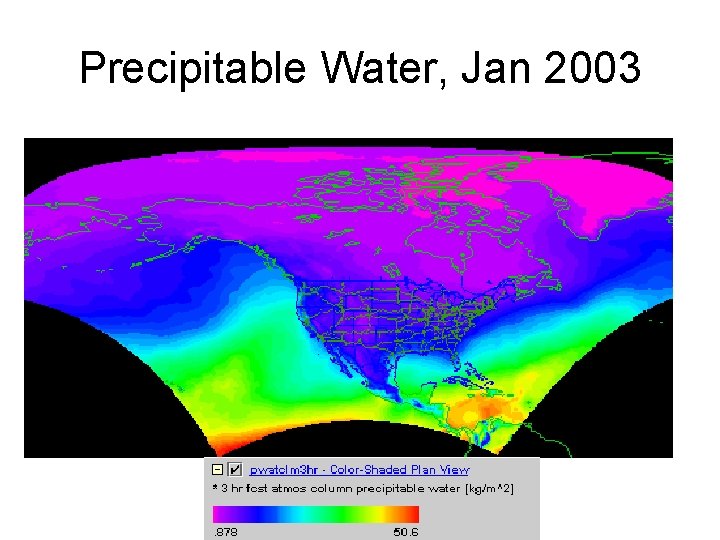
Precipitable Water, Jan 2003

Precipitable Water, July 2003

January July
- Slides: 34