Atmospheric phase correction Jan Martin Winters IRAM Grenoble

Atmospheric phase correction Jan Martin Winters IRAM, Grenoble Fourth IRAM Millimeter Interferometry School 2004: Atmospheric phase correction 1

The problem n n Atmosphere introduces (complex) refractive index => path delay + absorption/emission Water vapor poorly mixes with dry air => „eddies“ Atmosphere is turbulent => fluctuating path delay Time varying deformation of wavefront => Phase fluctuation => Degradation of source amplitude Degradation of spatial resolution Fourth IRAM Millimeter Interferometry School 2004: Atmospheric phase correction 2

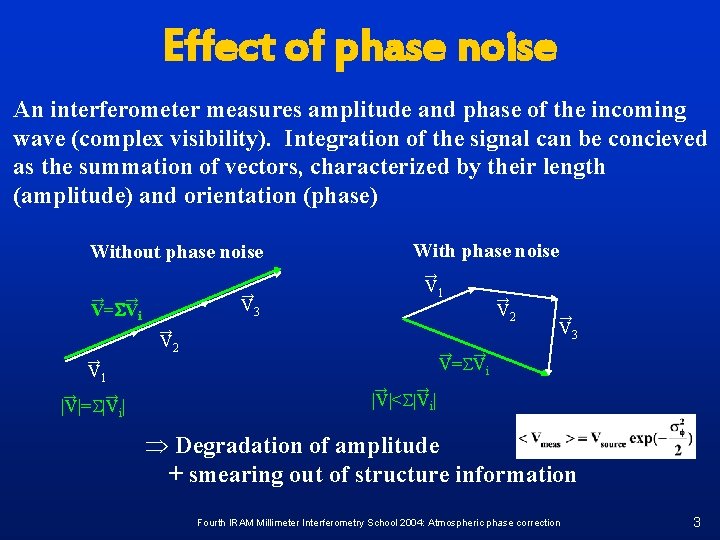
Effect of phase noise An interferometer measures amplitude and phase of the incoming wave (complex visibility). Integration of the signal can be concieved as the summation of vectors, characterized by their length (amplitude) and orientation (phase) With phase noise Without phase noise → → V 1 → → V 3 V=SVi → V 2 → V 1 → → |V|=S|Vi| → → V 3 → V=SVi → → |V|<S|Vi| Þ Degradation of amplitude + smearing out of structure information Fourth IRAM Millimeter Interferometry School 2004: Atmospheric phase correction 3

The idea n Determine the amount of water vapor in front of each telescope by measuring its emission n Deduce the path delay caused by this water column n Apply a corresponding phase correction Fourth IRAM Millimeter Interferometry School 2004: Atmospheric phase correction 4

The method Atmospheric emission Tsky = TAtm (1 - e-t) With t = td + tw = td + pwv Excess path L = Ld + LV = Ld + 6. 52 pwv [cm] Phase delay DF = 2 p DL /l = 2 p/l ( L/ Tsky) DTsky n => Measure Tsky (fluctuating) in front of each telescope Use atmospheric model to derive (t, TAtm, ) pwv, L/ Tsky n Compute phase correction DF and apply it to data n Fourth IRAM Millimeter Interferometry School 2004: Atmospheric phase correction 5

In practice (I): n Total power radiometry, e. g. , in the 1 mm band (a factor ~6 more sensitive to pwv than 3 mm band) using the astronomical receivers This was the standard method used at the Pd. BI until August 2004 n n n Problems: Clouds: large k, low n => large variations in Tsky, but only small effect on the path excess DL Measurement at only one frequency(band): effect of clouds cannot be removed Long-term stability of the astronomical receivers (which are designed for sensitivity) (important for absolute phase correction) Fourth IRAM Millimeter Interferometry School 2004: Atmospheric phase correction 6

In practice (II): B) Multi channel radiometry in a water line (here: at 22 GHz) using dedicated instruments (Rem. : ALMA will use the 183 GHz line) This is the standard method used at the Pd. BI since August 2004 n Advantages: Effect of clouds can be removed : Tsky, H 2 O = Tvapor + Tcloud = TAtm (1 - e-tv) + TCloud (1 - e-tc) , t. C ~ n 2 linearize cloud exponential term, measure at two frequencies, build weighted mean: DTdouble = Tsky , 1 – Tsky, 2 (n 1/n 2)2 = Tvapor, 1 – Tvapor, 2 (n 1/n 2)2 n Instruments designed for stability => absolute phase correction Fourth IRAM Millimeter Interferometry School 2004: Atmospheric phase correction 7

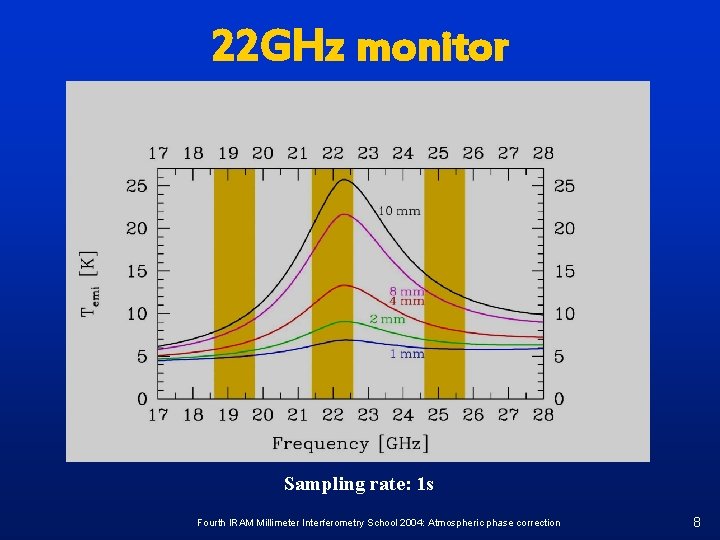
22 GHz monitor Sampling rate: 1 s Fourth IRAM Millimeter Interferometry School 2004: Atmospheric phase correction 8

Results 22 GHz correction (I) Temporal phase variation • • • unstable atmospheric conditions 4. 4 mm pwv phases @ 110 GHz A-configuration: E 23 -W 27 -N 29 -E 16 -W 23 -N 13 8 min on NRAO 150 Fourth IRAM Millimeter Interferometry School 2004: Atmospheric phase correction 9

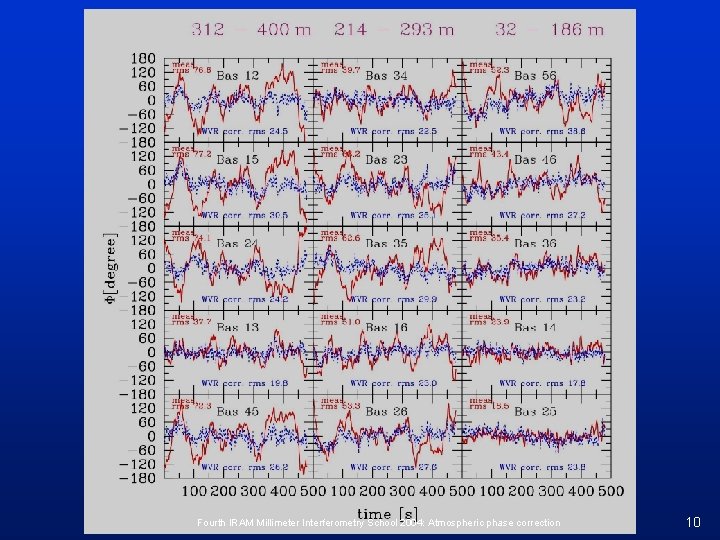
Fourth IRAM Millimeter Interferometry School 2004: Atmospheric phase correction 10

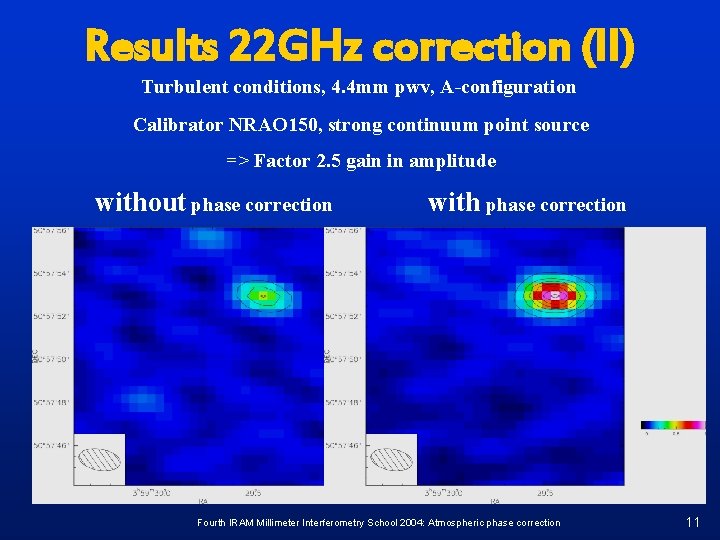
Results 22 GHz correction (II) Turbulent conditions, 4. 4 mm pwv, A-configuration Calibrator NRAO 150, strong continuum point source => Factor 2. 5 gain in amplitude without phase correction with phase correction Fourth IRAM Millimeter Interferometry School 2004: Atmospheric phase correction 11

Kolmogorov turbulence Turbulence is fed by energy input on large scales L (= outer scale of the turbulent field) This energy is cascaded down to smaller scales l (in a stationary process) until it is dissipated into heat on the smallest scales l 0 (inner scale) by viscosity The velocity fluctuation associated with linear scale l is vl, the typical time scale of the fluctuation is tl = l / vl Per unit mass, the rate at which energy is fed into eddies of size l is then e ~ vl 2 / t = vl 3 / l ( = v. L 3 / L) or vl ~ (el)1/3 Fourth IRAM Millimeter Interferometry School 2004: Atmospheric phase correction 12

Phase structure function Characterization of fluctuations by the structure function Dv(d) = < [v(x+d) - v(x)]2 > ≈ vd 2 ~ (ed)2/3 (velocity) Phase fluctuations are induced by fluctuations of the refractive index due to water vapor eddies in the turbulent atmosphere Dn(d) ~ (ed)2/3 (refractive index) On large scales (d ≫ height of turbulent layer, “thin screen”, 2 D) Df(d) ~ (ed)2/3 (phase, 2 D) On smaller scales: 3 D description, “thick screen” Df(d) ~ (ed)5/3 (phase, 3 D) For the rms phase noise sf = (Df(d))1/2 power law spectra are expected with exponents between 1/3 and 5/6 (On scales d > L: uncorrelated, Df(d) ≈ const) Fourth IRAM Millimeter Interferometry School 2004: Atmospheric phase correction 13

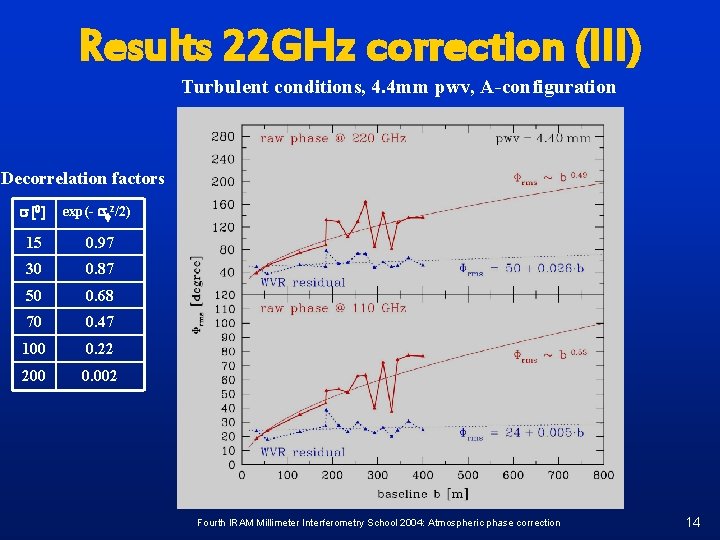
Results 22 GHz correction (III) Turbulent conditions, 4. 4 mm pwv, A-configuration Decorrelation factors s [0 ] exp(- sf 2/2) 15 0. 97 30 0. 87 50 0. 68 70 0. 47 100 0. 22 200 0. 002 Fourth IRAM Millimeter Interferometry School 2004: Atmospheric phase correction 14

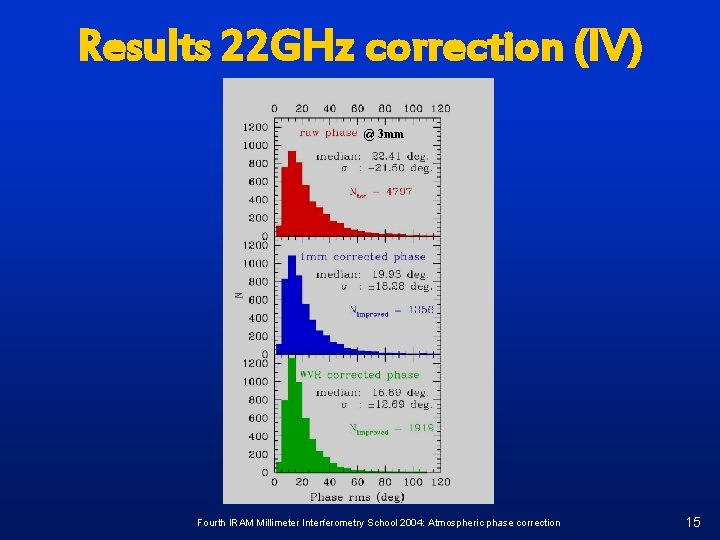
Results 22 GHz correction (IV) @ 3 mm Fourth IRAM Millimeter Interferometry School 2004: Atmospheric phase correction 15