Asynchronous logical networks I Digital Systems M 1

Asynchronous logical networks I Digital Systems M 1

The safe problem • The combination for opening a safe requires NOT the input of a combination of keys BUT a sequence (time depedent) of inputs. Only if the sequence is correct the safe opens • It means that the independent variable TIME has been implicitly introduced as an input • The input control network must therefore provided with memory in order to remember what happened in the past • The logical networks whose outputs do NOT depend ONLY from the present inputs but ALSO from the time (that is the temporal succession of the inputs and therefore from the memory of the past) are named SEQUENTIAL NETWORKS • The description of the sequential networks is therefore NOT based on a truth table but on a state diagram. The state represents the previous history of the system 2

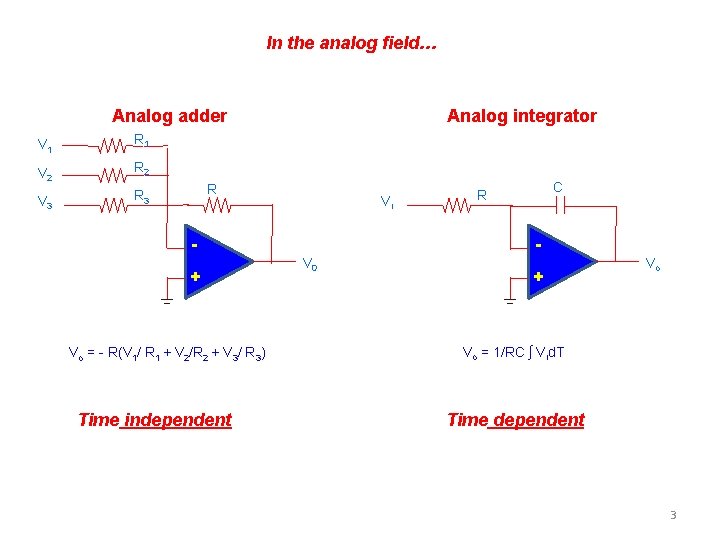
In the analog field… Analog integrator R 1 V 2 R 2 V 3 R + Vo = - R(V 1/ R 1 + V 2/R 2 + V 3/ R 3) Time independent Vi V 0 C R + V 1 - Analog adder Vo Vo = 1/RC ʃ Vid. T Time dependent 3

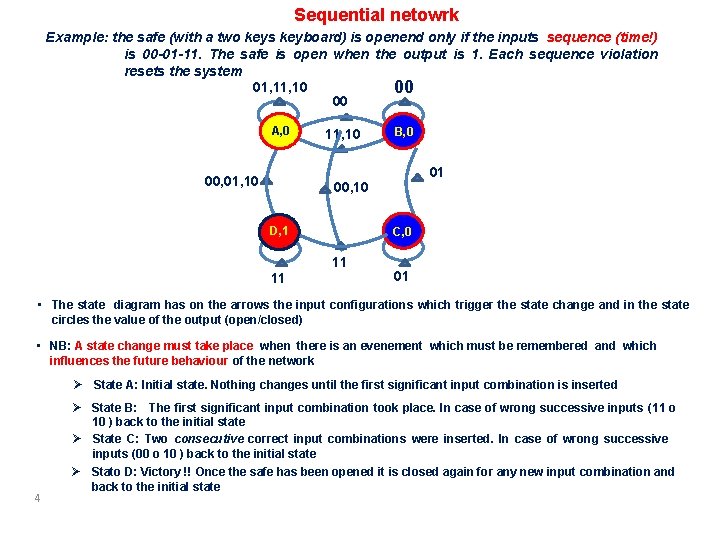
Sequential netowrk Example: the safe (with a two keys keyboard) is openend only if the inputs sequence (time!) is 00 -01 -11. The safe is open when the output is 1. Each sequence violation resets the system 01, 10 00 00 A, 0 00, 01, 10 11, 10 B, 0 01 00, 10 D, 1 C, 0 11 11 01 • The state diagram has on the arrows the input configurations which trigger the state change and in the state circles the value of the output (open/closed) • NB: A state change must take place when there is an evenement which must be remembered and which influences the future behaviour of the network Ø State A: Initial state. Nothing changes until the first significant input combination is inserted 4 Ø State B: The first significant input combination took place. In case of wrong successive inputs (11 o 10 ) back to the initial state Ø State C: Two consecutive correct input combinations were inserted. In case of wrong successive inputs (00 o 10 ) back to the initial state Ø Stato D: Victory !! Once the safe has been opened it is closed again for any new input combination and back to the initial state

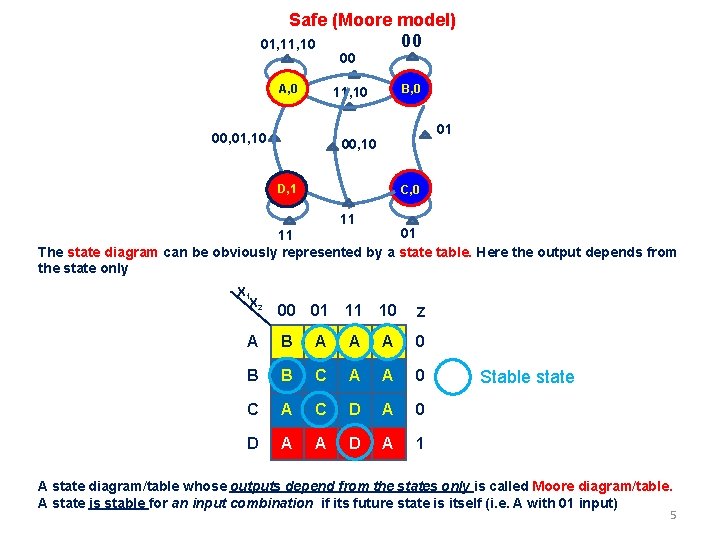
Safe (Moore model) 00 01, 10 00 A, 0 B, 0 11, 10 00, 01, 10 01 00, 10 D, 1 C, 0 11 01 11 The state diagram can be obviously represented by a state table. Here the output depends from the state only X 1 X 2 00 01 11 10 Z A B A A A 0 B B C A A 0 C A C D A 0 D A A D A 1 Stable state A state diagram/table whose outputs depend from the states only is called Moore diagram/table. A state is stable for an input combination if its future state is itself (i. e. A with 01 input) 5

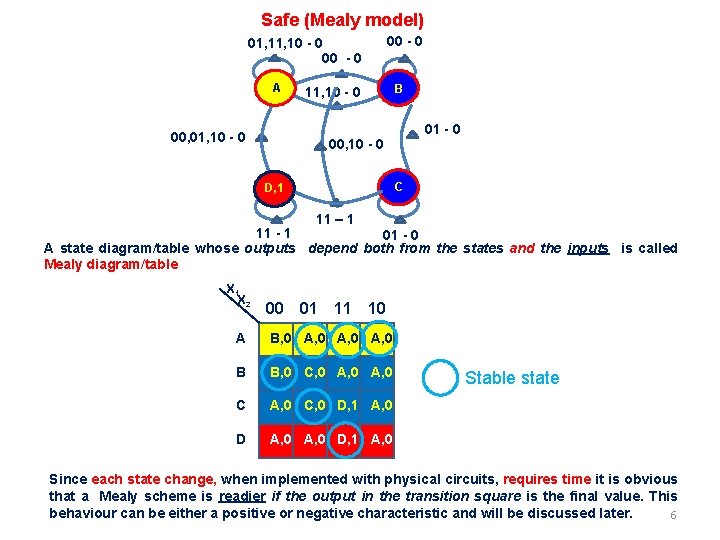
Safe (Mealy model) 01, 10 - 0 00 - 0 A 00, 01, 10 - 0 00 - 0 11, 10 - 0 B 01 - 0 00, 10 - 0 C D, 1 11 – 1 11 - 1 01 - 0 A state diagram/table whose outputs depend both from the states and the inputs is called Mealy diagram/table X 1 X 2 00 01 11 10 A B, 0 A, 0 B B, 0 C, 0 A, 0 C, 0 D, 1 A, 0 D, 1 A, 0 Stable state Since each state change, when implemented with physical circuits, requires time it is obvious that a Mealy scheme is readier if the output in the transition square is the final value. This behaviour can be either a positive or negative characteristic and will be discussed later. 6

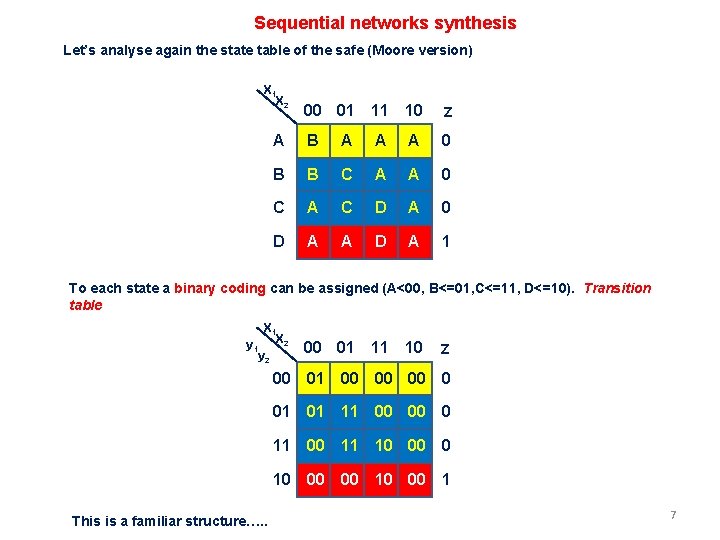
Sequential networks synthesis Let’s analyse again the state table of the safe (Moore version) X 1 X 2 00 01 11 10 Z A B A A A 0 B B C A A 0 C A C D A 0 D A A D A 1 To each state a binary coding can be assigned (A<00, B<=01, C<=11, D<=10). Transition table X 1 y 1 X 2 y 2 00 01 11 10 Z 00 01 00 00 00 0 01 01 11 00 00 0 11 00 11 10 00 00 10 00 1 This is a familiar structure…. . 7

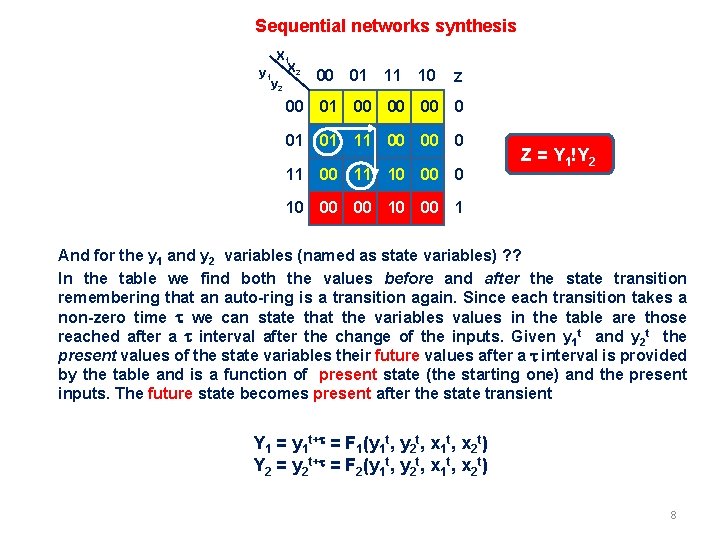
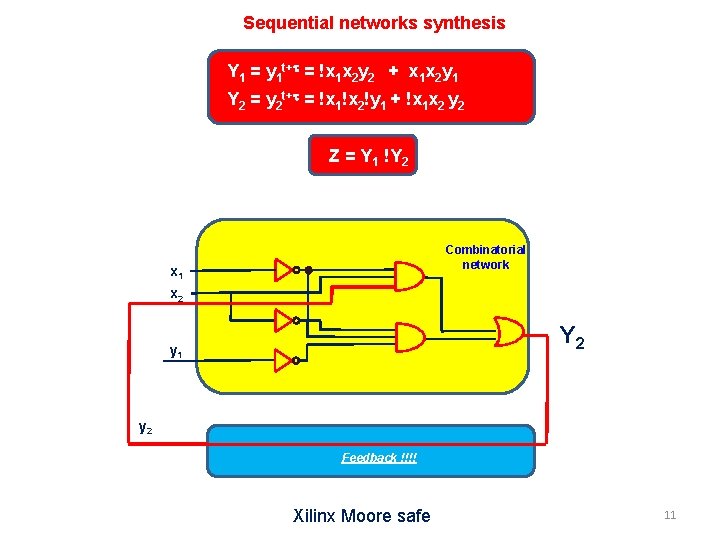
Sequential networks synthesis X 1 y 1 X 2 y 2 00 01 11 10 Z 00 01 00 00 00 0 01 01 11 00 00 0 11 00 11 10 00 0 Z = Y 1!Y 2 10 00 00 1 And for the y 1 and y 2 variables (named as state variables) ? ? In the table we find both the values before and after the state transition remembering that an auto-ring is a transition again. Since each transition takes a non-zero time t we can state that the variables values in the table are those reached after a t interval after the change of the inputs. Given y 1 t and y 2 t the present values of the state variables their future values after a t interval is provided by the table and is a function of present state (the starting one) and the present inputs. The future state becomes present after the state transient Y 1 = y 1 t+t = F 1(y 1 t, y 2 t, x 1 t, x 2 t) Y 2 = y 2 t+t = F 2(y 1 t, y 2 t, x 1 t, x 2 t) 8

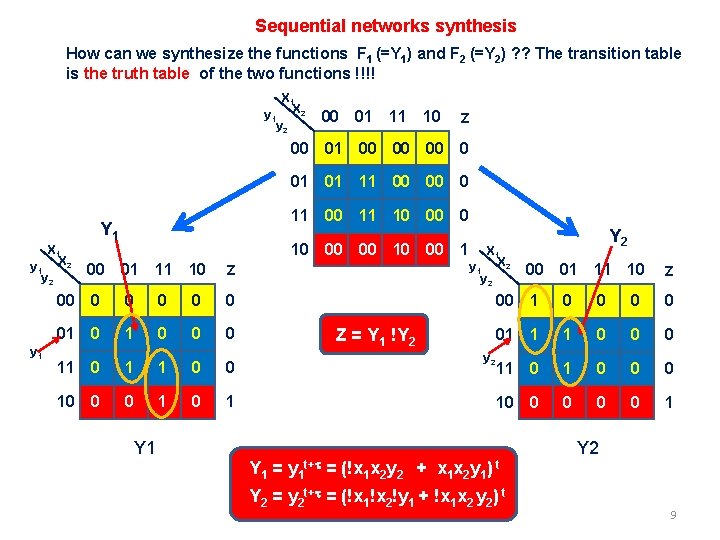
Sequential networks synthesis How can we synthesize the functions F 1 (=Y 1) and F 2 (=Y 2) ? ? The transition table is the truth table of the two functions !!!! X 1 y 1 X 2 y 2 00 01 11 10 Z 00 01 00 00 00 0 01 01 11 00 00 0 11 00 11 10 00 0 Y 1 X 1 y 1 X 2 y 1 10 00 00 1 00 01 11 10 Z 00 0 0 01 0 0 0 11 0 1 1 0 0 10 0 0 1 X 1 y 1 X 2 y 2 Z = Y 1 !Y 2 y 2 Y 2 00 01 11 10 Z 00 1 0 0 01 1 1 0 0 0 11 0 0 0 10 0 0 1 Y 2 Y 1 = y 1 t+t = (!x 1 x 2 y 2 + x 1 x 2 y 1) t Y 2 = y 2 t+t = (!x 1!x 2!y 1 + !x 1 x 2 y 2) t 9

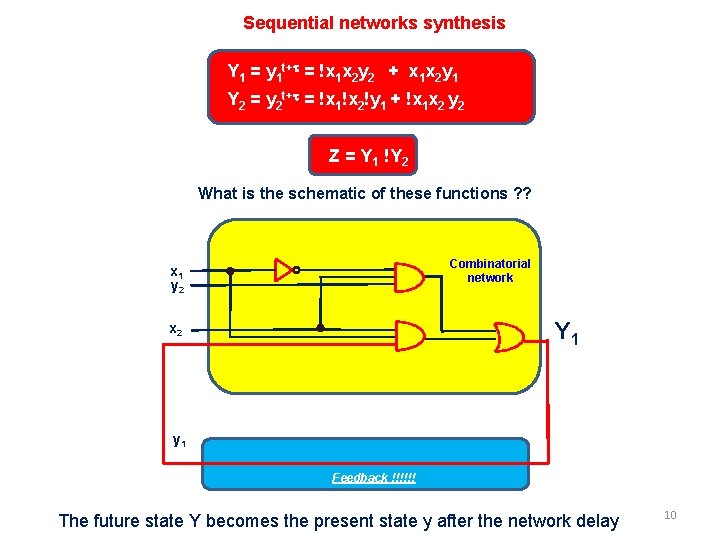
Sequential networks synthesis Y 1 = y 1 t+t = !x 1 x 2 y 2 + x 1 x 2 y 1 Y 2 = y 2 t+t = !x 1!x 2!y 1 + !x 1 x 2 y 2 Z = Y 1 !Y 2 What is the schematic of these functions ? ? Combinatorial network x 1 y 2 Y 1 x 2 y 1 Feedback !!!!!! The future state Y becomes the present state y after the network delay 10

Sequential networks synthesis Y 1 = y 1 t+t = !x 1 x 2 y 2 + x 1 x 2 y 1 Y 2 = y 2 t+t = !x 1!x 2!y 1 + !x 1 x 2 y 2 Z = Y 1 !Y 2 Combinatorial network x 1 x 2 Y 2 y 1 y 2 Feedback !!!! Xilinx Moore safe 11

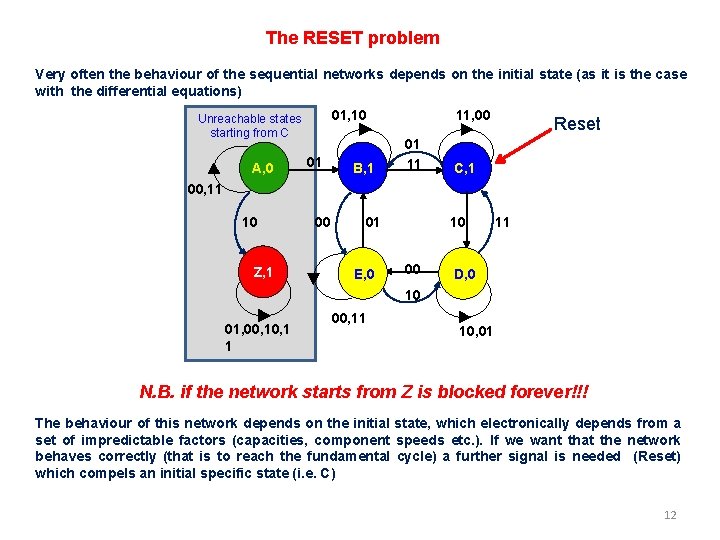
The RESET problem Very often the behaviour of the sequential networks depends on the initial state (as it is the case with the differential equations) 01, 10 Unreachable states starting from C A, 0 01 B, 1 11, 00 01 11 Reset C, 1 00, 11 10 Z, 1 00 01 E, 0 10 00 11 D, 0 10 01, 00, 1 1 00, 11 10, 01 N. B. if the network starts from Z is blocked forever!!! The behaviour of this network depends on the initial state, which electronically depends from a set of impredictable factors (capacities, component speeds etc. ). If we want that the network behaves correctly (that is to reach the fundamental cycle) a further signal is needed (Reset) which compels an initial specific state (i. e. C) 12

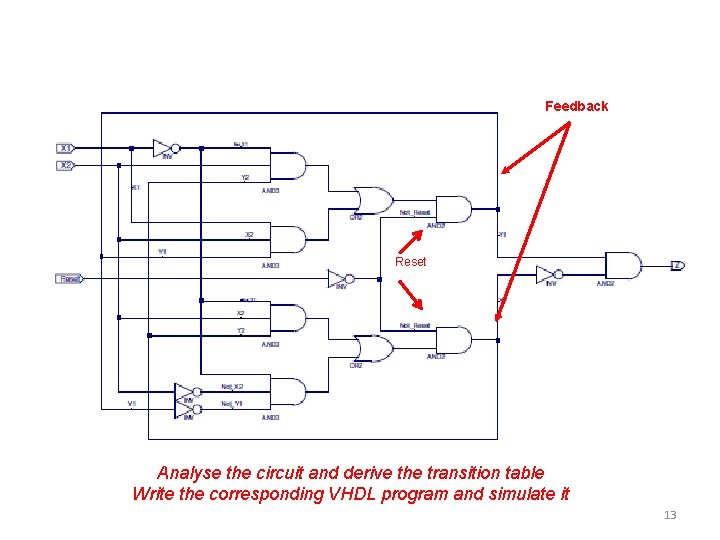
Feedback Reset Analyse the circuit and derive the transition table Write the corresponding VHDL program and simulate it 13

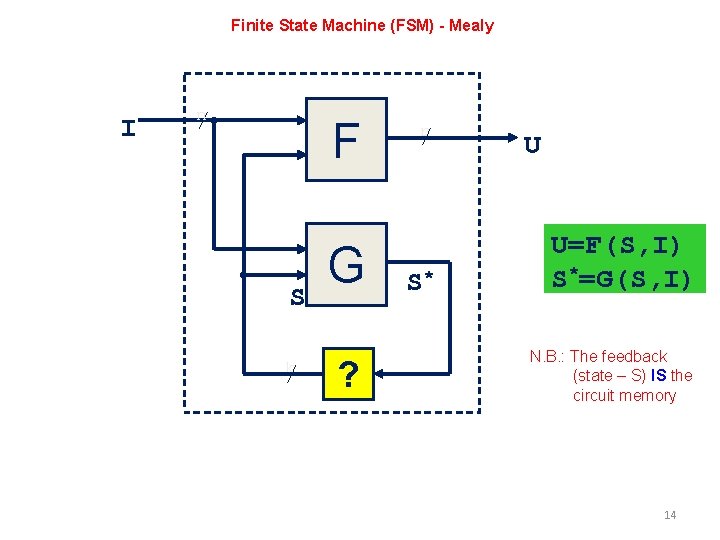
Finite State Machine (FSM) - Mealy I n F S k G ? r S* U U=F(S, I) S*=G(S, I) N. B. : The feedback (state – S) IS the circuit memory 14

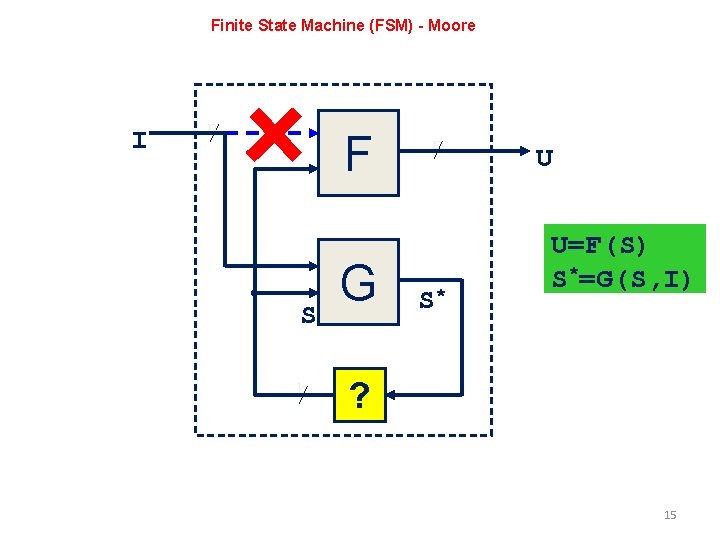
Finite State Machine (FSM) - Moore I n F S k G r S* U U=F(S) S*=G(S, I) ? 15

Mealy network And if the table is Mealy type (see the state diagram)? X 1 y 1 X 2 y 2 00 01 11 10 00 01, 0 00, 0 01 01, 0 11, 0 00, 0 11, 0 10, 1 00, 0 10, 1 10, 0 Z = X 1 X 2 Y 1 The state variables synthesis is obviously the same As far as the states are concerned the transition table obviously doesn’t change but the output function changes. In this case the network is more «ready» but more complex. This is generally the case with the Mealy networks. It must be noticed that in the squares where a state transition occurs and the output(s) change, for the changing outputs a «don’t care» can be inserted which could have a positive effect on the complexity of the function. Obviously in case of output change it is possible to keep in the square either the previous value or to insert the final value: in the first case we implement a network less ready to react to the new inputs; the contrary occurs in the latter case. If we insert a don’t care it means that it is not importat whether the network is more or less ready to react (it will depend on the synthesis - Karnaugh map) 16

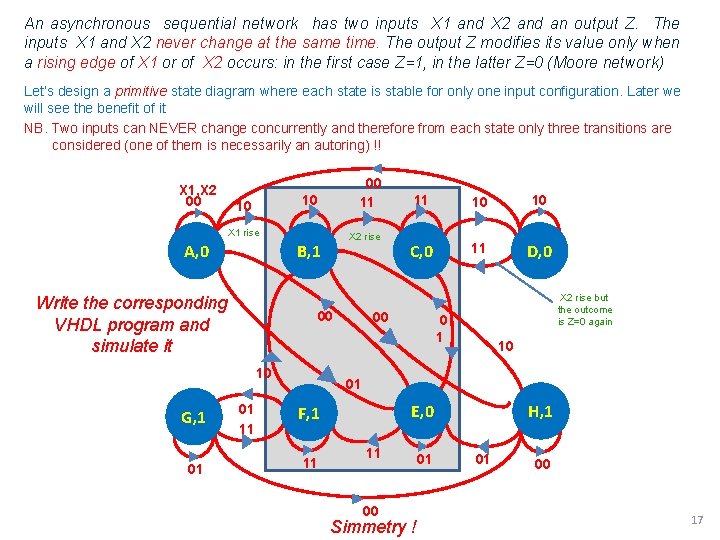
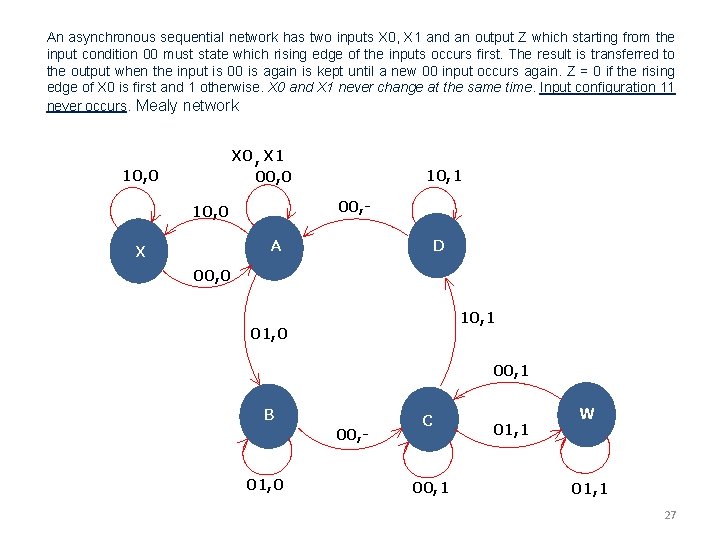
An asynchronous sequential network has two inputs X 1 and X 2 and an output Z. The inputs X 1 and X 2 never change at the same time. The output Z modifies its value only when a rising edge of X 1 or of X 2 occurs: in the first case Z=1, in the latter Z=0 (Moore network) Let’s design a primitive state diagram where each state is stable for only one input configuration. Later we will see the benefit of it NB. Two inputs can NEVER change concurrently and therefore from each state only three transitions are considered (one of them is necessarily an autoring) !! 00 X 1, X 2 00 10 10 11 X 1 rise A, 0 B, 1 Write the corresponding VHDL program and simulate it 00 10 G, 1 01 X 2 rise 01 11 11 10 10 C, 0 11 D, 0 00 X 2 rise but the outcome is Z=0 again 0 1 10 01 E, 0 F, 1 11 11 00 Simmetry ! 01 H, 1 01 00 17

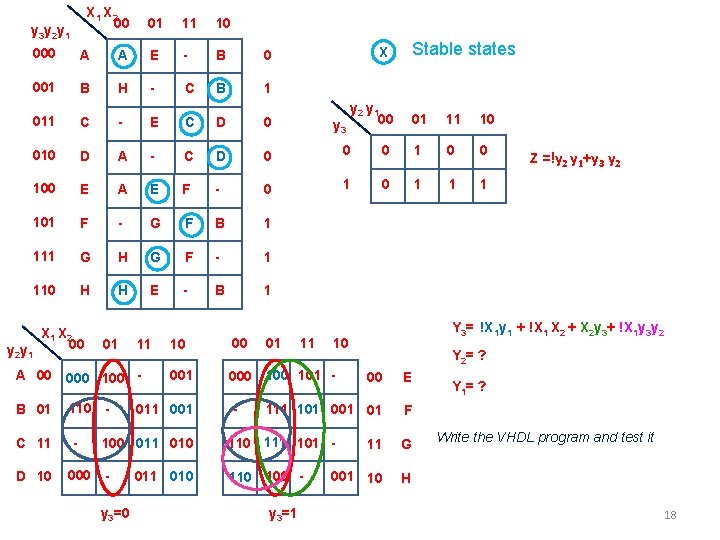
X 1 X 2 00 y 3 y 2 y 1 01 11 10 A A E - B 0 001 B H - C B 1 011 C - E C D 0 010 D A - C D 0 0 100 E A E F - 0 1 101 F - G F B 1 111 G H G F - 1 110 H H E - B 1 X 2 00 y 2 y 1 01 11 A 00 000 100 B 01 110 - C 11 - D 10 00 001 000 101 - 100 011 010 000 y 3=0 y 2 y 1 00 y 3 10 011 001 010 - 01 Stable states X 000 11 01 11 10 0 1 0 0 0 1 1 1 Y 3= !X 1 y 1 + !X 1 X 2 + X 2 y 3+ !X 1 y 3 y 2 10 Y 2= ? 00 E 111 101 01 F 110 111 101 110 100 y 3=1 Z =!y 2 y 1+y 3 y 2 11 G 001 10 H Y 1= ? Write the VHDL program and test it 18

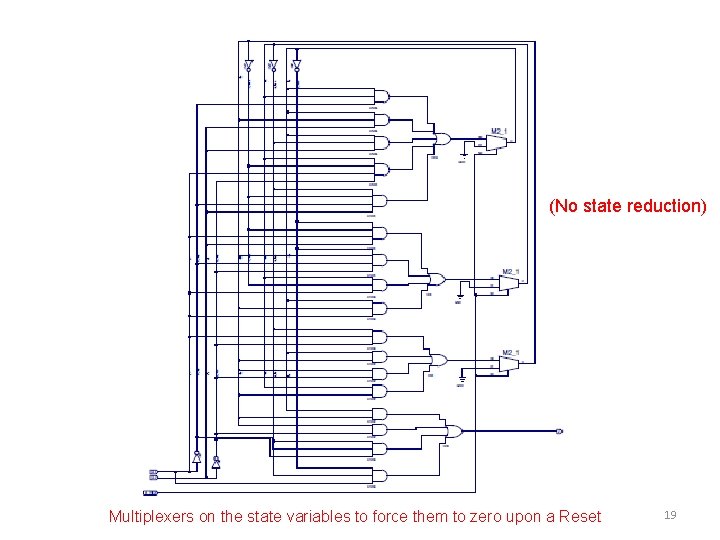
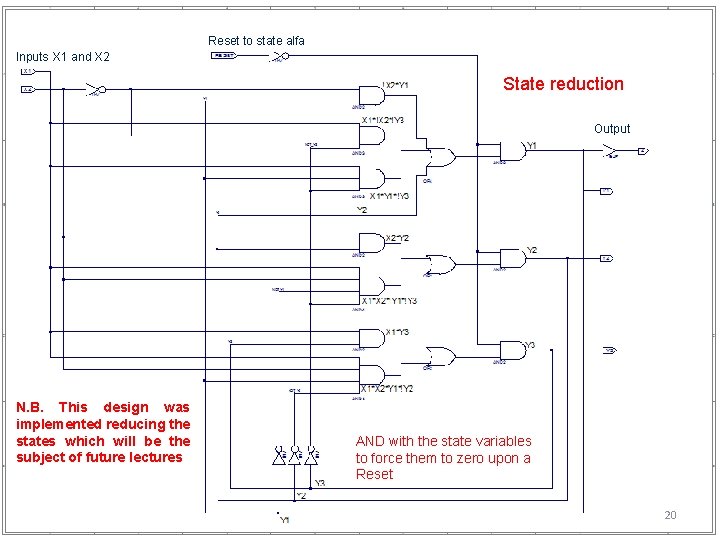
(No state reduction) Multiplexers on the state variables to force them to zero upon a Reset 19

Reset to state alfa Inputs X 1 and X 2 State reduction Output N. B. This design was implemented reducing the states which will be the subject of future lectures AND with the state variables to force them to zero upon a Reset 20

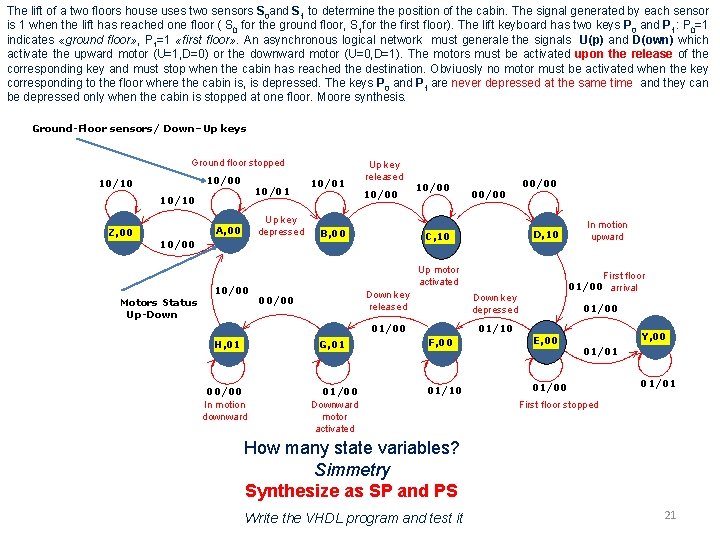
The lift of a two floors house uses two sensors S 0 and S 1 to determine the position of the cabin. The signal generated by each sensor is 1 when the lift has reached one floor ( S 0 for the ground floor, S 1 for the first floor). The lift keyboard has two keys P 0 and P 1: P 0=1 indicates «ground floor» , P 1=1 «first floor» . An asynchronous logical network must generale the signals U(p) and D(own) which activate the upward motor (U=1, D=0) or the downward motor (U=0, D=1). The motors must be activated upon the release of the corresponding key and must stop when the cabin has reached the destination. Obviuosly no motor must be activated when the key corresponding to the floor where the cabin is, is depressed. The keys P 0 and P 1 are never depressed at the same time and they can be depressed only when the cabin is stopped at one floor. Moore synthesis. Ground-Floor sensors/ Down–Up keys Ground floor stopped 10/00 10/10 10/01 10/10 Z, 00 Up key depressed A, 00 10/00 Motors Status Up-Down 10/00 10/01 Up key released 10/00 B, 00 10/00 00/00 D, 10 C, 10 Up motor activated 00/00 H, 01 G, 01 00/00 In motion downward 01/00 Downward motor activated Down key released Down key depressed 01/00 01/10 In motion upward First floor 01/00 arrival 01/00 F, 00 E, 00 01/10 01/00 Y, 00 01/01 First floor stopped How many state variables? Simmetry Synthesize as SP and PS Write the VHDL program and test it 21

Another design (similar) The lift of a two floors house uses 2 sensors S 0, S 1 to determine the position of the cabin. The output of each sensor is 1 when the cabin is at the specific floor (S 0 ground floor , S 1 first floor). The control keyboard is made of two keys P 0 and P 1: P 0=1 indicates a downward command, P 1=1 indicates an upward command. An asynchronous network must generate the signals U(p) and D(own) to trigger the two motors upward (U=1, D=0) or downwards (U=0, D=1). NB In this case we must not wait for the release of a key to activate the motor Direct synthesis implementation The control functions of the two motors U(p) and D(own) are: U= !D!S 1 P 1 + U!S 1 D= !U!S 0 P 0 + D!S 0 The upward motor U (downward D) is activated only if: D (U) not active, the first floor sensor S 1 (ground S 0) is ‘ 0’ and P 1 (P 0) is depressed. In this case U (D) is active until S 1 (S 0) is activated [+ U!S 1] [+ U!S 0]. Write the VHDL program and test it 22

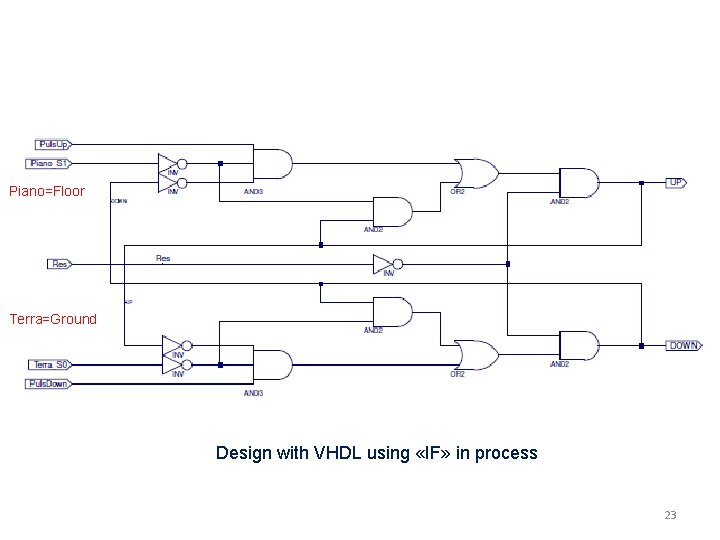
Piano=Floor Terra=Ground Design with VHDL using «IF» in process 23

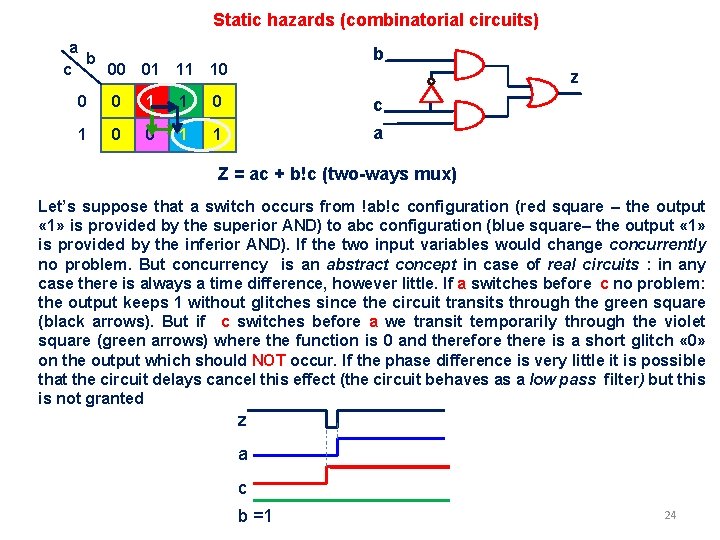
Static hazards (combinatorial circuits) a b c 00 01 11 10 b z 0 0 1 1 0 c 1 0 0 1 1 a Z = ac + b!c (two-ways mux) Let’s suppose that a switch occurs from !ab!c configuration (red square – the output « 1» is provided by the superior AND) to abc configuration (blue square– the output « 1» is provided by the inferior AND). If the two input variables would change concurrently no problem. But concurrency is an abstract concept in case of real circuits : in any case there is always a time difference, however little. If a switches before c no problem: the output keeps 1 without glitches since the circuit transits through the green square (black arrows). But if c switches before a we transit temporarily through the violet square (green arrows) where the function is 0 and therefore there is a short glitch « 0» on the output which should NOT occur. If the phase difference is very little it is possible that the circuit delays cancel this effect (the circuit behaves as a low pass filter) but this is not granted z a c b =1 24

Static hazards a bc 00 01 11 10 0 0 1 1 Z = !ac + ab (!abc + !a!bc + ab!c) Let’s suppose we want to switch from square a=b=c=1 to a=0 b=c=1. Theoretically the output should remain 1. But if (as it is possible) a becomes 0 (and therefore abc=0) before !a becomes 1 (and therefore !abc is still 0) the output has a zero glitch which constitutes a real danger (as it will be shown later) In this case the problem can be solved with a redundant synthesis that is with Z = !ac + ab + bc. The term bc (which is 1 during the transition of a) grants stability to the output. The proposed solution is not always possible 25

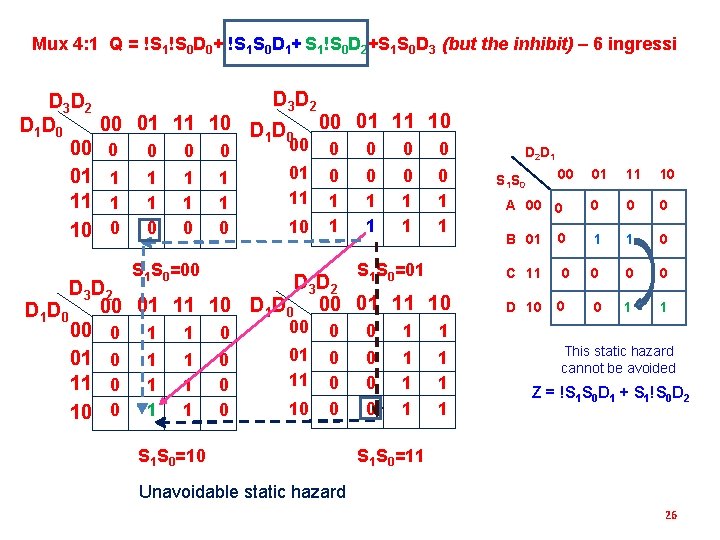
Mux 4: 1 Q = !S 1!S 0 D 0+ !S 1 S 0 D 1+ S 1!S 0 D 2+S 1 S 0 D 3 (but the inhibit) – 6 ingressi D 3 D 2 D 1 D 0 00 01 11 10 D 3 D 2 00 01 11 10 D D 1 0 0 1 1 0 00 01 11 10 0 0 1 1 S 1 S 0=00 0 0 1 1 S S =01 0 0 1 1 1 0 D 3 D 2 00 01 11 10 D 1 D 0 00 01 11 10 D 1 D 0 00 0 1 1 01 0 1 1 0 11 0 0 1 1 11 0 1 1 0 0 1 1 10 0 1 1 0 S 1 S 0=10 D 2 D 1 00 01 11 10 A 00 0 0 B 01 0 1 1 0 C 11 0 0 0 1 1 S 1 S 0 D 10 0 This static hazard cannot be avoided Z = !S 1 S 0 D 1 + S 1!S 0 D 2 S 1 S 0=11 Unavoidable static hazard 26

An asynchronous sequential network has two inputs X 0, X 1 and an output Z which starting from the input condition 00 must state which rising edge of the inputs occurs first. The result is transferred to the output when the input is 00 is again is kept until a new 00 input occurs again. Z = 0 if the rising edge of X 0 is first and 1 otherwise. X 0 and X 1 never change at the same time. Input configuration 11 never occurs. Mealy network X 0 , X 1 00, 0 10, 1 00, - 10, 0 A X D 00, 0 10, 1 01, 0 00, 1 B 00, 01, 0 C 00, 1 01, 1 W 01, 1 27

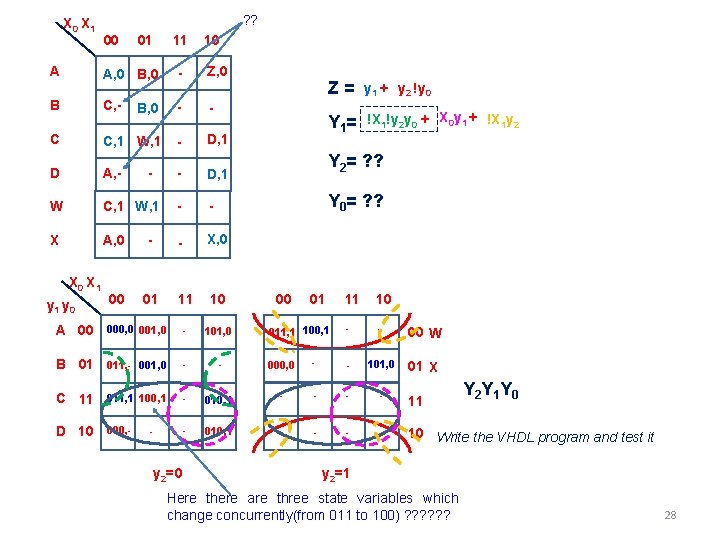
X 0 X 1 A ? ? 00 01 11 10 A, 0 B, 0 - Z, 0 B C, - B, 0 - - C C, 1 W, 1 - D, 1 D A, - - D, 1 W C, 1 W, 1 - - X A, 0 - - X, 0 00 01 11 10 X 1 y 0 - Z= y 1 + y 2 !y 0 Y 1= !X 1!y 2 y 0 + X 0 y 1 + !X 1 y 2 Y 2= ? ? Y 0= ? ? 00 01 11 10 - - 00 W 01 X A 00 000, 0 001, 0 - 101, 0 B 01 011, - 001, 0 - - 000, 0 - - 101, 0 C 11 011, 1 100, 1 - 010, 1 - - 11 D 10 000, - - 010, 1 - - 10 Write the VHDL program and test it - y 2=0 011, 1 100, 1 Y 2 Y 1 Y 0 y 2=1 Here there are three state variables which change concurrently(from 011 to 100) ? ? ? 28

(reduced states) Vivado Design Never_together 29

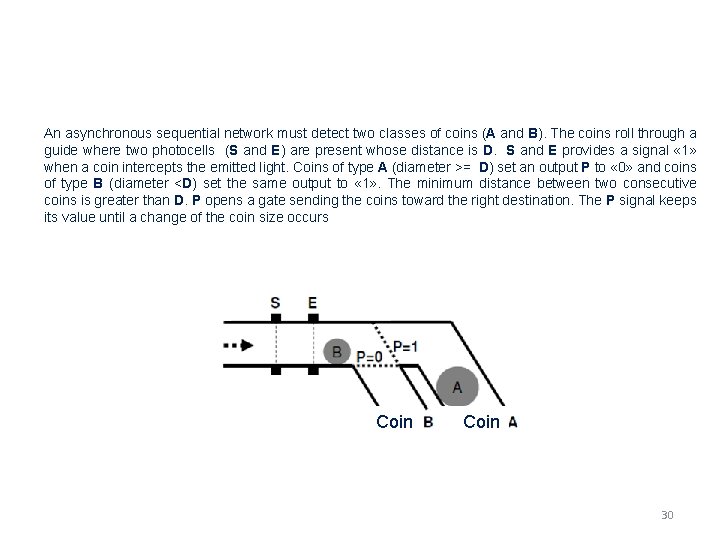
An asynchronous sequential network must detect two classes of coins (A and B). The coins roll through a guide where two photocells (S and E) are present whose distance is D. S and E provides a signal « 1» when a coin intercepts the emitted light. Coins of type A (diameter >= D) set an output P to « 0» and coins of type B (diameter <D) set the same output to « 1» . The minimum distance between two consecutive coins is greater than D. P opens a gate sending the coins toward the right destination. The P signal keeps its value until a change of the coin size occurs Coin 30

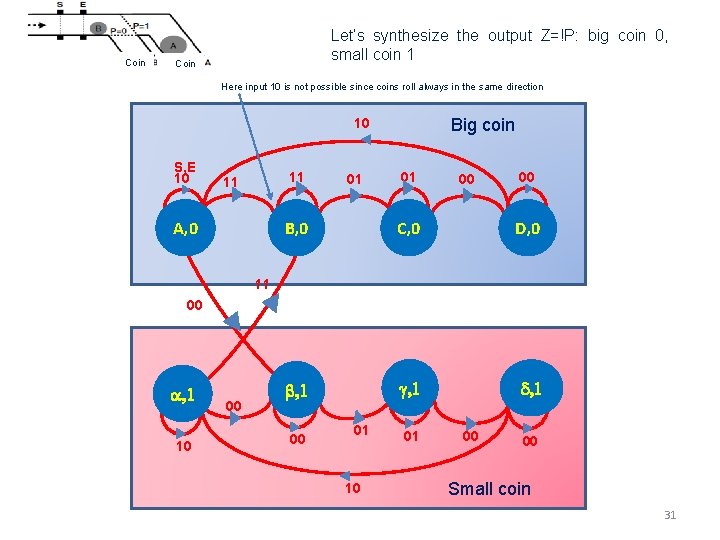
Coin Let’s synthesize the output Z=!P: big coin 0, small coin 1 Coin Here input 10 is not possible since coins roll always in the same direction Big coin 10 S, E 10 11 11 A, 0 01 01 00 00 B, 0 C, 0 D, 0 b, 1 g, 1 d, 1 11 00 a, 1 10 00 00 01 10 01 00 00 Small coin 31

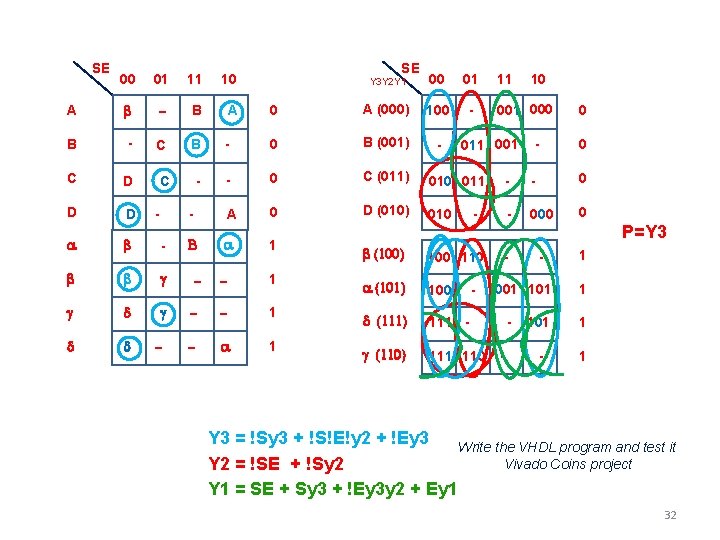
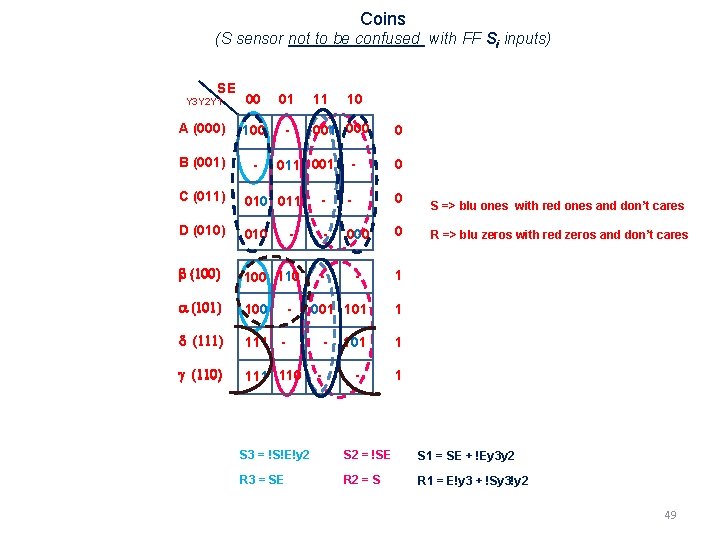
SE 00 01 11 10 A b - B A B - C B C D C - D D a b - b b g g d d d SE Y 3 Y 2 Y 1 00 01 0 A (000) 100 - - 0 B (001) - - 0 C (011) 010 011 - - 0 - A 0 D (010) 010 - 000 0 B a 1 - - 1 g - - 1 - - a 1 - 11 000 011 001 - b (100) 100 110 a (101) 100 d (111) 111 - g (110) 111 110 - 001 101 - 0 0 P=Y 3 1 101 1 - 1 Y 3 = !Sy 3 + !S!E!y 2 + !Ey 3 Write the VHDL program and test it Vivado Coins project Y 2 = !SE + !Sy 2 Y 1 = SE + Sy 3 + !Ey 3 y 2 + Ey 1 32

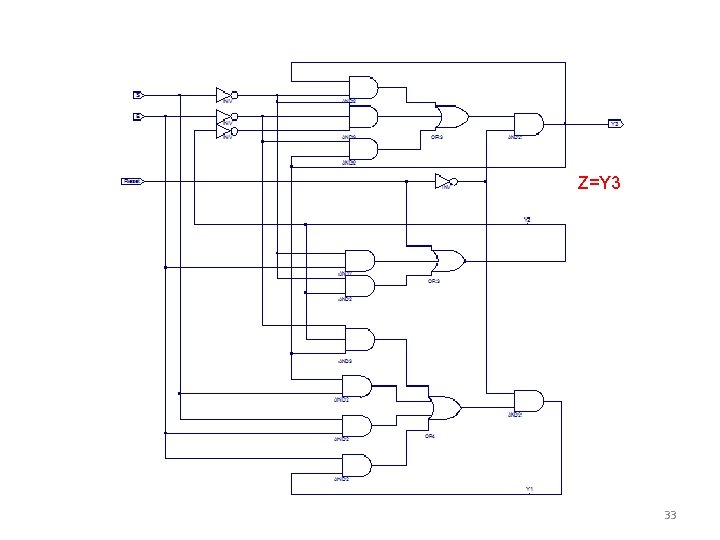
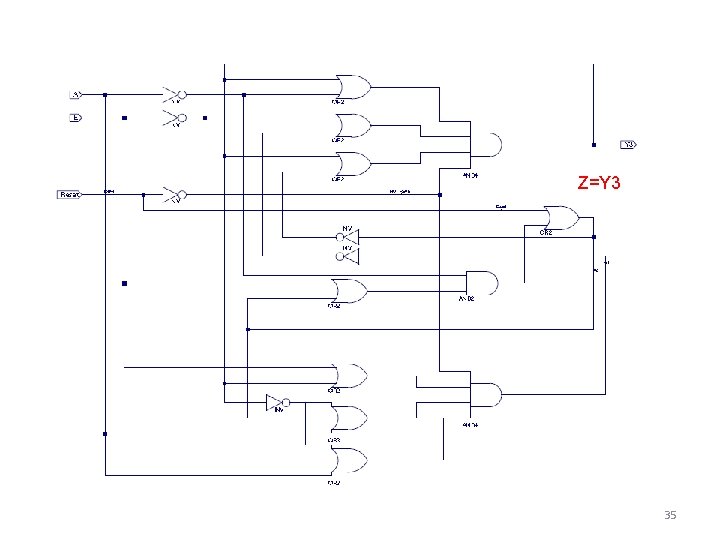
Z=Y 3 33

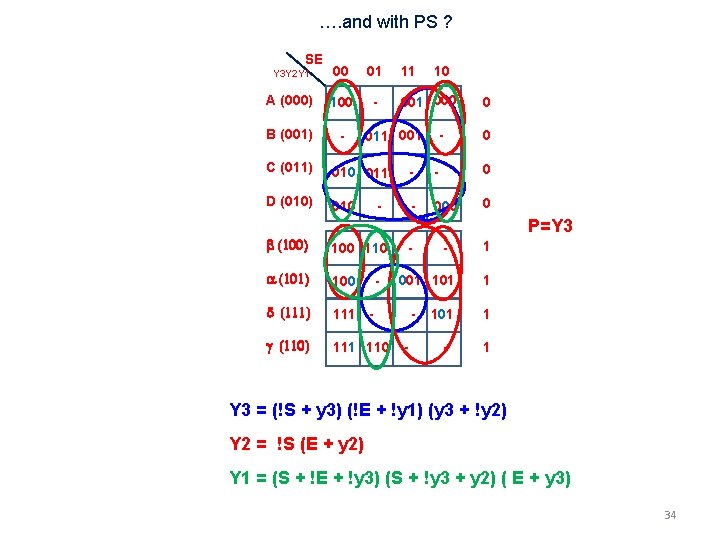
…. and with PS ? SE Y 3 Y 2 Y 1 00 01 A (000) 100 - B (001) - 11 10 001 000 011 001 - 0 0 C (011) 010 011 - - 0 D (010) 010 - 000 0 - P=Y 3 b (100) 100 110 a (101) 100 d (111) 111 - g (110) 111 110 - - - 001 101 - 1 1 101 1 - 1 Y 3 = (!S + y 3) (!E + !y 1) (y 3 + !y 2) Y 2 = !S (E + y 2) Y 1 = (S + !E + !y 3) (S + !y 3 + y 2) ( E + y 3) 34

Z=Y 3 35

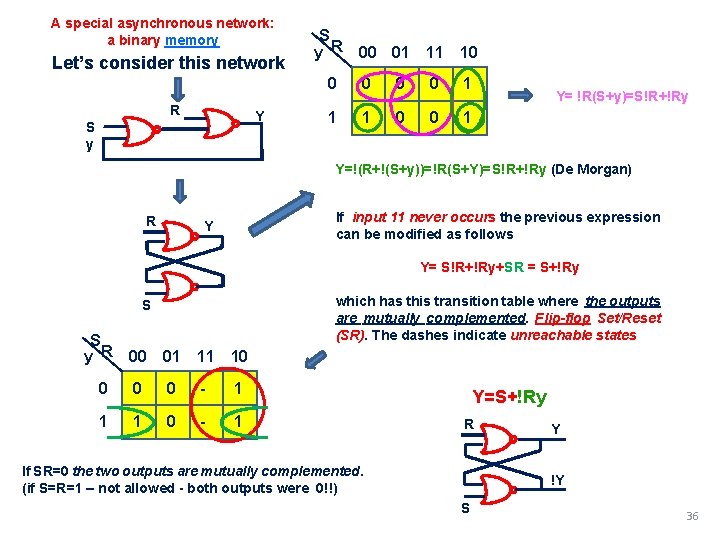
A special asynchronous network: a binary memory Let’s consider this network R Y S y R 00 01 11 10 0 0 1 1 1 0 0 1 Y= !R(S+y)=S!R+!Ry Y=!(R+!(S+y))=!R(S+Y)=S!R+!Ry (De Morgan) R If input 11 never occurs the previous expression can be modified as follows Y Y= S!R+!Ry+SR = S+!Ry which has this transition table where the outputs are mutually complemented. Flip-flop Set/Reset (SR). The dashes indicate unreachable states S S y R 00 01 11 10 0 - 1 1 1 0 - 1 Y=S+!Ry R If SR=0 the two outputs are mutually complemented. (if S=R=1 – not allowed - both outputs were 0!!) Y !Y S 36

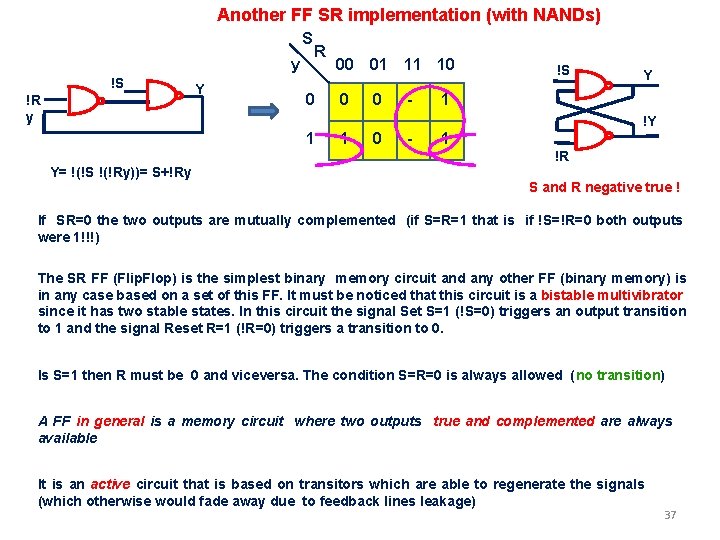
Another FF SR implementation (with NANDs) S y !S !R y Y R 0 00 01 11 10 0 0 - !S Y 1 !Y 1 1 0 - 1 !R Y= !(!S !(!Ry))= S+!Ry S and R negative true ! If SR=0 the two outputs are mutually complemented (if S=R=1 that is if !S=!R=0 both outputs were 1!!!) The SR FF (Flip. Flop) is the simplest binary memory circuit and any other FF (binary memory) is in any case based on a set of this FF. It must be noticed that this circuit is a bistable multivibrator since it has two stable states. In this circuit the signal Set S=1 (!S=0) triggers an output transition to 1 and the signal Reset R=1 (!R=0) triggers a transition to 0. Is S=1 then R must be 0 and viceversa. The condition S=R=0 is always allowed (no transition) A FF in general is a memory circuit where two outputs true and complemented are always available It is an active circuit that is based on transitors which are able to regenerate the signals (which otherwise would fade away due to feedback lines leakage) 37

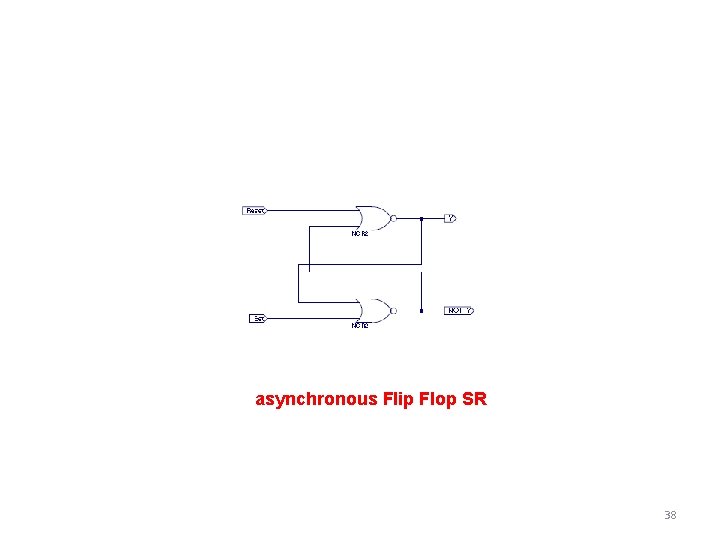
asynchronous Flip Flop SR 38

FF SR_1 entity FF_SR_1 is Port ( S : in std_logic; R : in std_logic; Q : out std_logic; QN : out std_logic); end FF_SR_1; architecture Behavioral of FF_SR_1 is -- NB «signal» declaration after architecture and before begin) !!! signal QN_feedback : std_logic : = '0'; signal Q_feedback begin : std_logic : = ‘ 1'; -- NB: in this implementation no process Q_feedback <= R nor QN; QN_feedback <= S nor Q; Q <= Q_feedback; QN <= QN_feedback; -- four statements simultaneous end Behavioral; 39

FF SR_2 (when-else) entity FF_SR_2 is Port ( S : in std_logic; R : in std_logic; Q : out std_logic; QN : out std_logic); end FF_SR_2; architecture Behavioral of FF_SR_2 is signal Q_internal : std_logic; signal QN_internal: std_logic; begin -- NB in this implementation no process Q_internal <= '1' when (S='1' and R='0') else -'0' when (S='0' and R='1') else --Q_internal; -QN_internal <= when without select Conditions are tested in sequence and are therefore alternative '0' when (S='1' and R='0') else '1' when (S='0' and R='1') else QN_internal; -- and with S=R=1 ? ? ? Q <= Q_internal; QN <= QN_internal; end Behavioral; 40

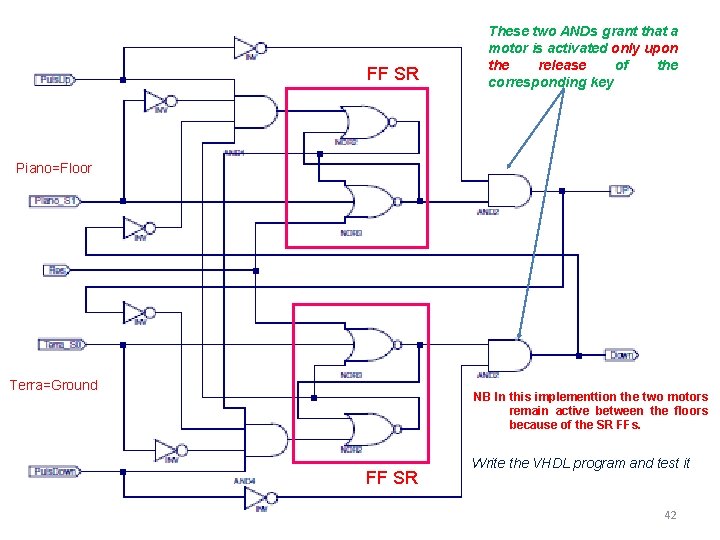
Example II asynchronous – Direct synthesis - SR based The lift of a two floors house uses two sensors S 0 and S 1 to determine the position of the cabin. The signal generated by each sensor is 1 when the lift has reached one floor ( S 0 for the ground floor, S 1 for the first floor). The lift keyboard has two keys P 0 and P 1: P 0=1 indicates «ground floor» , P 1=1 «first floor» . An asynchronous logical network must generale the signals U(p) and D(own) which activate the upward motor (U=1, D=0) or the downward motor (U=0, D=1). The motors must be activated upon the release of the corresponding key and must stop when the cabin has reached the destination. Obviously no motor must be activated when the key corresponding to the floor where the cabit is, is depressed. The keys P 0 and P 1 are never depressed at the same time and they can be depressed only when the cabin is stopped at one floor. Moore synthesis. The sensors Floor (S 1) and Ground(S 0) are input variables. A SR FF which drives the UP motor (Down) is activated when the key Puls. Up (Puls. Down) is depressed, the other motor SR FF is 0, the cabin is at the ground floor S 0 (first floor S 1) and reset RES=0. Res=1 deactivates both motors FF. In order to grant that the motor UP (Down) is activated upon the relase of Puls. Up (Puls. Down) a final AND whose inputs are the SR FF output Up(Down) and !Puls. Up (!Puls. Down) is inserted. 41

FF SR These two ANDs grant that a motor is activated only upon the release of the corresponding key Piano=Floor Terra=Ground NB In this implementtion the two motors remain active between the floors because of the SR FFs. FF SR Write the VHDL program and test it 42

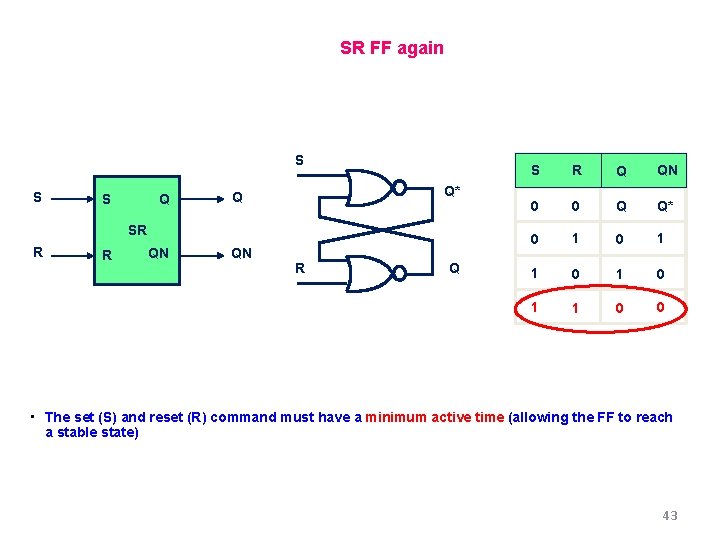
SR FF again S S Q* Q SR R R QN QN R Q S R Q QN 0 0 Q Q* 0 1 0 1 1 0 0 • The set (S) and reset (R) command must have a minimum active time (allowing the FF to reach a stable state) 43

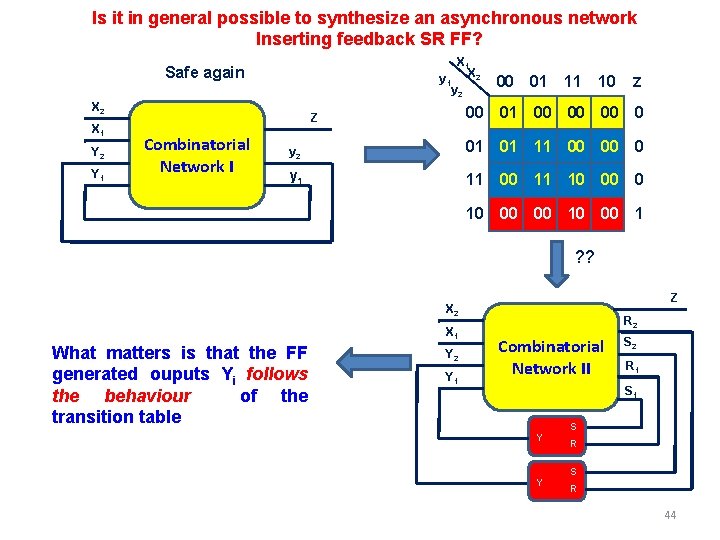
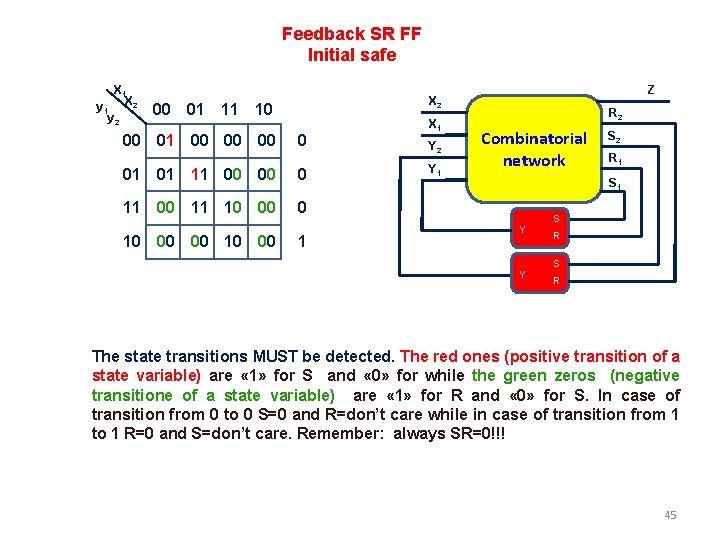
Is it in general possible to synthesize an asynchronous network Inserting feedback SR FF? X 1 y 1 X 2 y 2 Safe again X 2 X 1 Y 2 Y 1 Z 00 01 00 00 00 0 Z Combinatorial Network I 00 01 11 10 y 2 01 01 11 00 00 0 y 1 11 00 11 10 00 00 10 00 1 ? ? Z X 2 X 1 What matters is that the FF generated ouputs Yi follows the behaviour of the transition table Y 2 Y 1 R 2 Combinatorial Network II S 2 R 1 S 1 Y Y S R 44

Feedback SR FF Initial safe X 1 y 1 X 2 y 2 00 01 11 10 00 01 00 00 00 0 01 01 11 00 00 0 11 00 11 10 00 00 10 00 Z X 2 1 X 1 Y 2 Y 1 R 2 Combinatorial network S 2 R 1 S 1 Y Y S R The state transitions MUST be detected. The red ones (positive transition of a state variable) are « 1» for S and « 0» for while the green zeros (negative transitione of a state variable) are « 1» for R and « 0» for S. In case of transition from 0 to 0 S=0 and R=don’t care while in case of transition from 1 to 1 R=0 and S=don’t care. Remember: always SR=0!!! 45

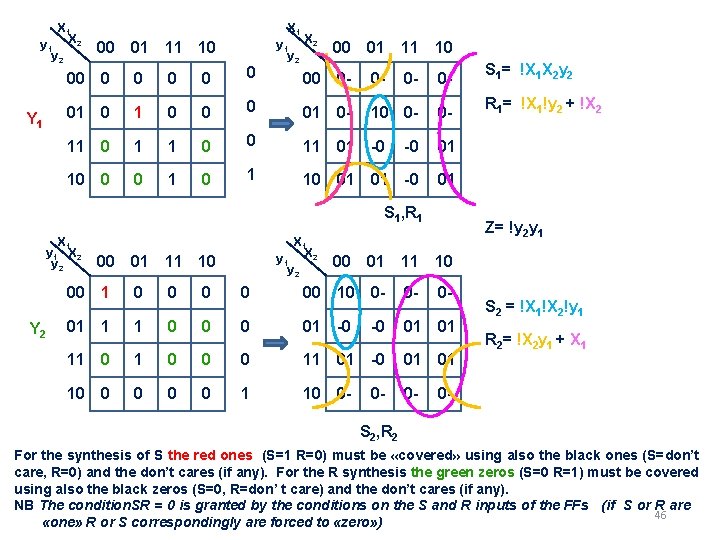
X 1 y 1 X 2 y 2 Y 1 X 1 y 1 00 01 11 10 X 2 y 2 00 01 11 10 00 0 - 0 - S 1= !X 1 X 2 y 2 0 01 0 - 10 0 - 0 - R 1= !X 1!y 2 + !X 2 0 0 11 01 -0 -0 01 0 1 10 01 01 -0 01 00 0 0 01 0 0 11 0 1 1 10 0 0 1 S 1, R 1 X 1 y 1 X 2 y 2 Y 2 X 1 y 1 X 2 y 2 00 01 11 10 Z= !y 2 y 1 00 01 11 10 00 1 0 0 00 10 0 - 0 - 01 1 1 0 01 -0 -0 01 01 11 0 0 0 11 01 -0 01 01 10 0 0 1 10 0 - 0 - S 2 = !X 1!X 2!y 1 R 2= !X 2 y 1 + X 1 0 - S 2, R 2 For the synthesis of S the red ones (S=1 R=0) must be «covered» using also the black ones (S=don’t care, R=0) and the don’t cares (if any). For the R synthesis the green zeros (S=0 R=1) must be covered using also the black zeros (S=0, R=don’ t care) and the don’t cares (if any). NB The condition. SR = 0 is granted by the conditions on the S and R inputs of the FFs (if S or R are 46 «one» R or S correspondingly are forced to «zero» )

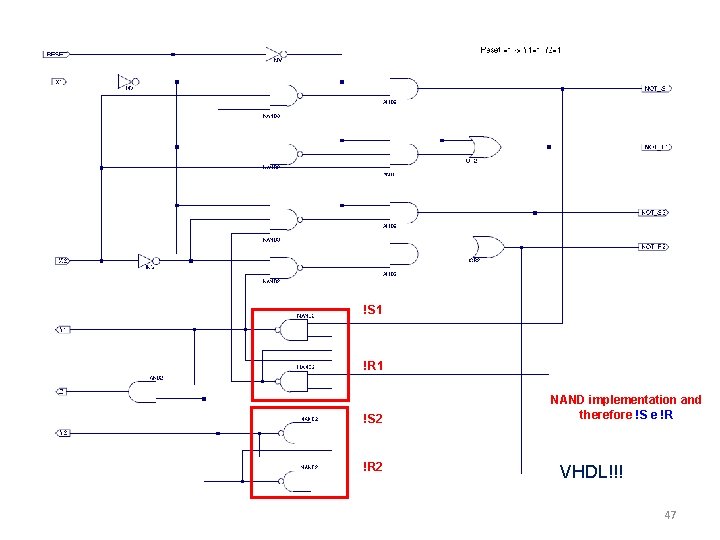
!S 1 !R 1 !S 2 !R 2 NAND implementation and therefore !S e !R VHDL!!! 47

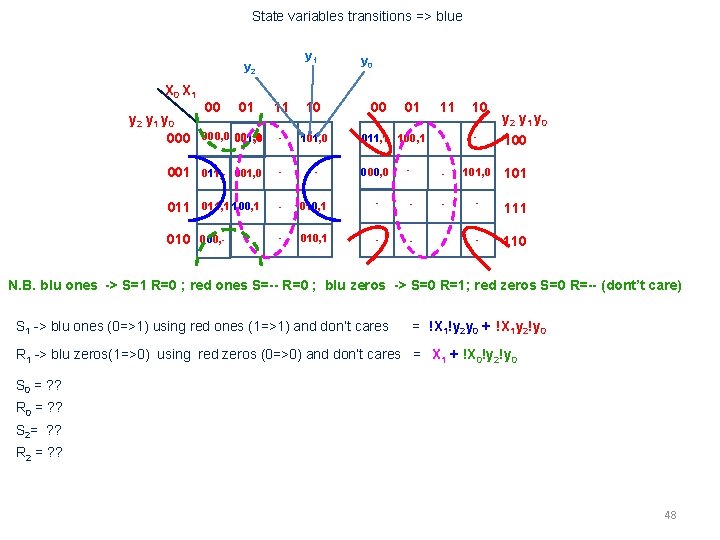
State variables transitions => blue y 1 y 2 X 0 X 1 11 10 000, 0 001, 0 - 101, 0 001 011, - 001, 0 - - 000, 0 011 100, 1 011, 1 100, 1 - 010, 1 010 000, - - 010, 1 y 2 y 1 y 0 00 01 y 0 - 00 01 11 10 - - 101, 0 101 - - - - 110 011, 1 100, 1 y 2 y 1 y 0 N. B. blu ones -> S=1 R=0 ; red ones S=-- R=0 ; blu zeros -> S=0 R=1; red zeros S=0 R=-- (dont’t care) S 1 -> blu ones (0=>1) using red ones (1=>1) and don’t cares = !X 1!y 2 y 0 + !X 1 y 2!y 0 R 1 -> blu zeros(1=>0) using red zeros (0=>0) and don’t cares = X 1 + !X 0!y 2!y 0 S 0 = ? ? R 0 = ? ? S 2= ? ? R 2 = ? ? 48

Coins (S sensor not to be confused with FF Si inputs) SE Y 3 Y 2 Y 1 00 01 A (000) 100 - B (001) - 11 10 001 000 011 001 - 0 0 C (011) 010 011 - - 0 D (010) 010 - 000 0 b (100) 100 110 - - 1 a (101) 100 d (111) 111 - g (110) 111 110 - - 001 101 - S => blu ones with red ones and don’t cares R => blu zeros with red zeros and don’t cares 1 101 1 - 1 S 3 = !S!E!y 2 S 2 = !SE S 1 = SE + !Ey 3 y 2 R 3 = SE R 2 = S R 1 = E!y 3 + !Sy 3!y 2 49

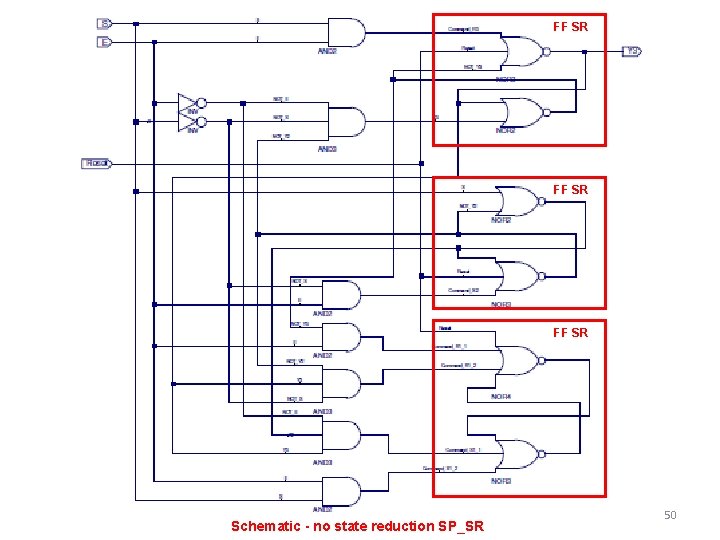
FF SR Schematic - no state reduction SP_SR 50

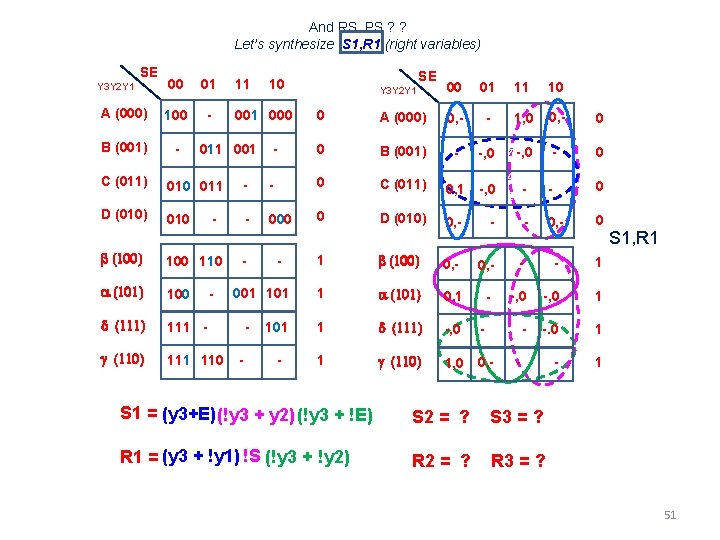
And RS PS ? ? Let’s synthesize S 1, R 1 (right variables) SE 00 01 A (000) 100 - B (001) - Y 3 Y 2 Y 1 11 000 011 001 SE 10 - Y 3 Y 2 Y 1 00 01 11 10 0 A (000) 0, - - 1, 0 0, - 0 B (001) zzzzzz -, 0 zzzzzz - 0, 1 -, 0 zzzzzzz 0 0, - - 0, - 0 C (011) 010 011 - - 0 C (011) D (010) 010 - 000 0 D (010) - b (100) 100 110 a (101) 100 d (111) 111 - g (110) 111 110 - - 0 S 1, R 1 1 b (100) 0, - - - 1 1 a (101) 0, 1 - -, 0 1 101 1 d (111) -, 0 - -. 0 1 - 1 g (110) 1, 0 0, - - 1 - 001 101 - - 0 - S 1 = (y 3+E)(!y 3 + y 2)(!y 3 + !E) S 2 = ? S 3 = ? R 1 = (y 3 + !y 1) !S (!y 3 + !y 2) R 2 = ? R 3 = ? 51

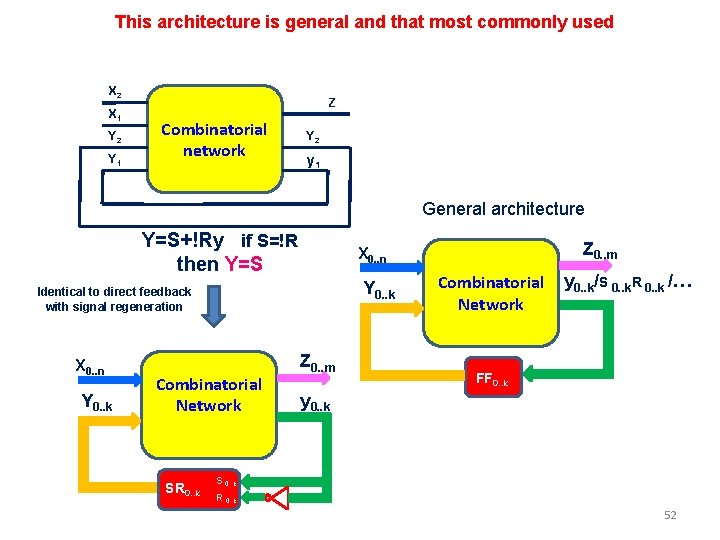
This architecture is general and that most commonly used X 2 X 1 Y 2 Y 1 Z Combinatorial network Y 2 y 1 General architecture Y=S+!Ry if S=!R then Y=S Y 0. . k Identical to direct feedback with signal regeneration X 0. . n Y 0. . k Combinatorial Network SR 0. . k Z 0. . m X 0. . n Z 0. . m Combinatorial Network y 0. . k/S 0. . k. R 0. . k /… FF 0. . k y 0. . k S 0. . k R 0. . k 52

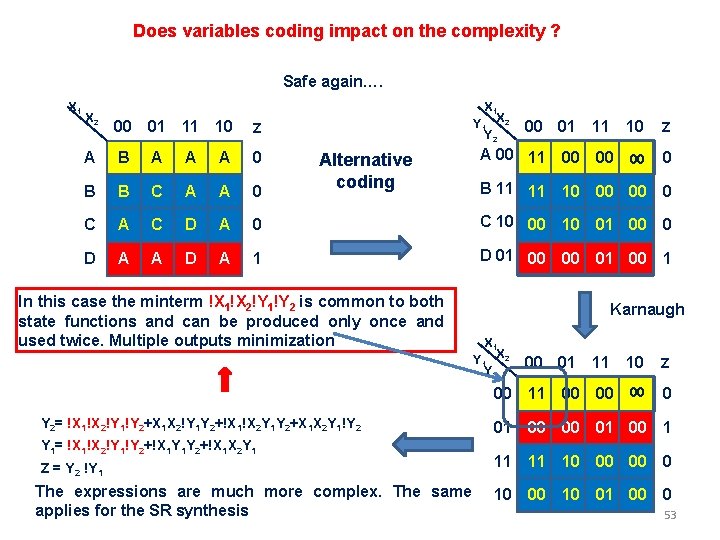
Does variables coding impact on the complexity ? Safe again…. X 1 Y 1 X 2 Y 2 X 2 00 01 11 10 Z A B A A A 0 B B C A A 0 C A C D A 0 C 10 00 10 01 00 0 D A A D A 1 D 01 00 00 01 00 1 Alternative coding In this case the minterm !X 1!X 2!Y 1!Y 2 is common to both state functions and can be produced only once and used twice. Multiple outputs minimization 00 01 11 10 A 00 11 00 00 Y 1= !X 1!X 2!Y 1!Y 2+!X 1 Y 1 Y 2+!X 1 X 2 Y 1 Z = Y 2 !Y 1 The expressions are much more complex. The same applies for the SR synthesis 0 B 11 11 10 00 00 0 Karnaugh X 1 Y 1 X 2 Y 2 00 01 11 10 Z 00 0 00 11 00 00 Y 2= !X 1!X 2!Y 1!Y 2+X 1 X 2!Y 1 Y 2+!X 1!X 2 Y 1 Y 2+X 1 X 2 Y 1!Y 2 00 Z 01 00 00 01 00 1 11 11 10 00 00 0 10 01 00 0 53

54