Asymptotic Analysis and Optimization in Metamaterials Heterogeneous Layers

Asymptotic Analysis and Optimization in Metamaterials: Heterogeneous Layers G. Leugering, E. Rohan, F. Seifrt Department of Mathematics University of Erlangen-Nürnberg and University of Pilsen PDE-Opt. Design-Numa/Workshop Benasque, 24. 8. -4. 09 G. Leugering, AM 2, FAU Erlangen-Nürnberg 1

Cloaking: problem formulation (Mathematical treatment: Uhlmann, Kohn, Bouchitte, Felbacq, Vogelius…. ) Object to be cloaked: here a ball G. Leugering, AM 2, FAU Erlangen-Nürnberg Object to be cloaked: Claoking layer 2

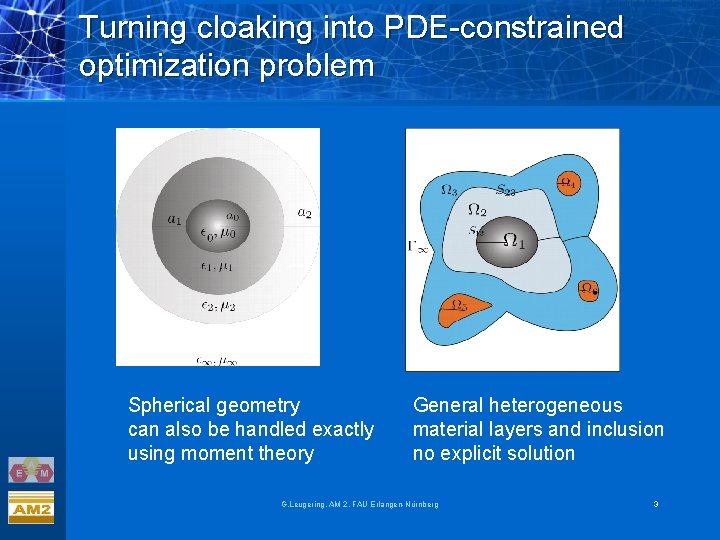
Turning cloaking into PDE-constrained optimization problem Spherical geometry can also be handled exactly using moment theory General heterogeneous material layers and inclusion no explicit solution G. Leugering, AM 2, FAU Erlangen-Nürnberg 3

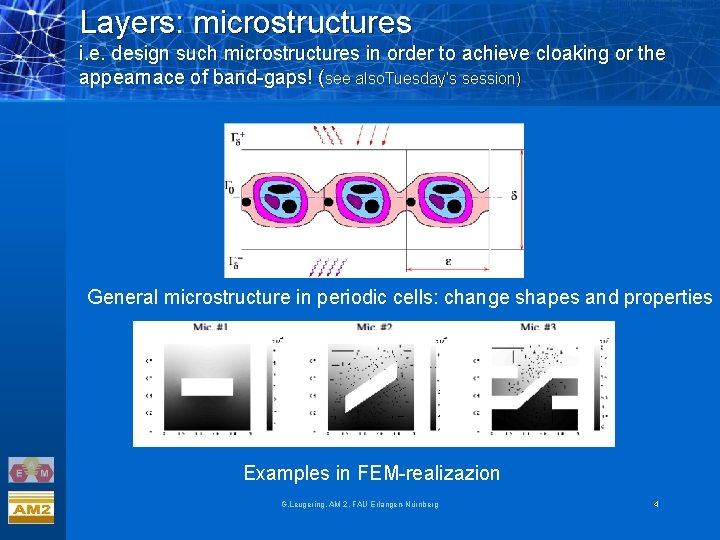
Layers: microstructures i. e. design such microstructures in order to achieve cloaking or the appearnace of band-gaps! (see also. Tuesday‘s session) General microstructure in periodic cells: change shapes and properties Examples in FEM-realizazion G. Leugering, AM 2, FAU Erlangen-Nürnberg 4

Time harmonics for elastodynamics G. Leugering, AM 2, FAU Erlangen-Nürnberg 5

Piezoelectricity: strong form (shape analysis of time varying problems: Novotny, Perla-Menzal, Sokolowski, G. L. 2009) G. Leugering, AM 2, FAU Erlangen-Nürnberg 6

Homogenized mass tensor G. Leugering, AM 2, FAU Erlangen-Nürnberg 7

Homogenized elasticity tensor G. Leugering, AM 2, FAU Erlangen-Nürnberg 8

Homogenized Helmholtz-type elasticity G. Leugering, AM 2, FAU Erlangen-Nürnberg 9

Metamaterial: e. g. negative mass! G. Leugering, AM 2, FAU Erlangen-Nürnberg 10

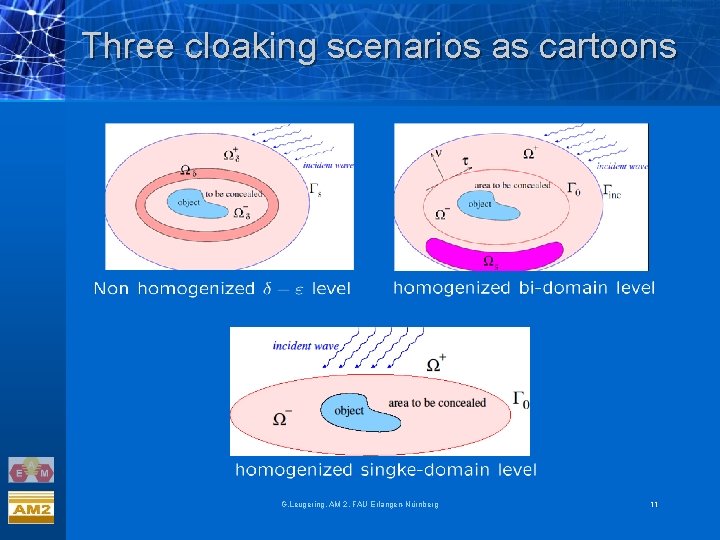
Three cloaking scenarios as cartoons G. Leugering, AM 2, FAU Erlangen-Nürnberg 11

Notation G. Leugering, AM 2, FAU Erlangen-Nürnberg 12

Cost function G. Leugering, AM 2, FAU Erlangen-Nürnberg 13

The non-homogenized problem G. Leugering, AM 2, FAU Erlangen-Nürnberg 14

Optimization on the G. Leugering, AM 2, FAU Erlangen-Nürnberg level 15

The limiting bi-domain problem G. Leugering, AM 2, FAU Erlangen-Nürnberg 16

The far-field optimization problem G. Leugering, AM 2, FAU Erlangen-Nürnberg 17

The simplest boundary-coefficient control problem G. Leugering, AM 2, FAU Erlangen-Nürnberg 18