Asymmetric Communication Complexity And its implications on Cell

Asymmetric Communication Complexity And its implications on Cell Probe Complexity Based on a paper of Peter Bro Miltersen, Noam Nisan, Muli Safra and Avi Wigderson Slides by Elad Verbin

Purpose We want to get Lower Bounds. Best known lower bounds: l Sorting is Ω(nlogn) in the comparison model l Trivial lower bounds. i. e. MAX is Ω(n) l What can we really do, i. e. for RAM?

Outline Yao decided to strengthen the model – Considered the Cell Probe model. l Lower bounding Cell Probe is hard too. We strengthen even more – Communication Complexity l

Outline l l 1. 2. We show the relationship between Cell Probe and Communication Complexity. We show to get lower bounds for Communication Complexity using two techniques: The Richness Technique The Round Elimination Technique

Communication Complexity The problem : f: X Y {0, 1} l Alice gets x X, Bob gets y Y, their goal is to exchange messages to decide f(x, y). l f(x, y) l A solution is a communication protocol that can compute f(x, y) for all x, y.

Asymmetric Communication Complexity l A Communication Protocol that computes function f in which Alice sends at most a bits and Bob sends at most b bits is called a [a, b]-protocol for f. Pink<=a f(x, y) Blue<=b

Randomized Protocols If the protocol is allowed to flip (public) coins, and gives the correct answer with probability > 2/3 it is called a randomized protocol. l If it always correctly identifies a 0 -instance it is called a one-sided error protocol. l

Example For any problem, there are trivial deterministic protocols: l [log|X|, 1]-protocol l [1, log|Y|]-protocol. l

The Problem DISJ(N, k, l) We work on the universe U={0, 1, …, N-1} l Alice gets x, a set of k elements l Bob gets y, a set of l elements l They must decide if x∩y=Ø l x y x∩y=Ø? =Ø

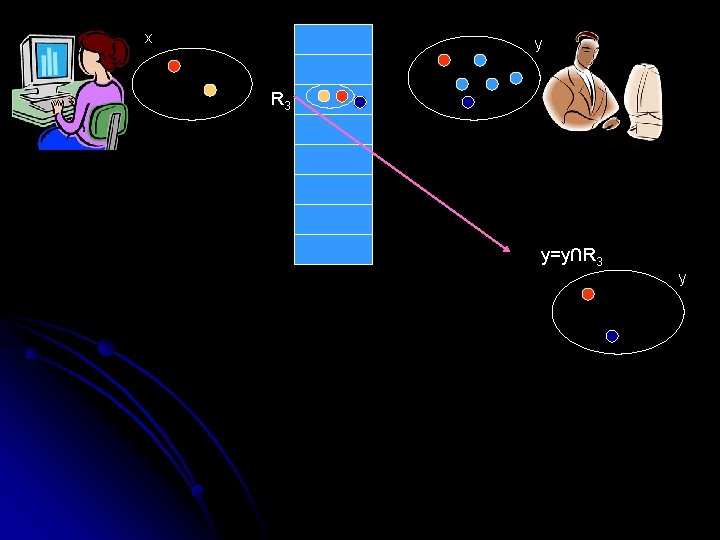
A one-sided error randomized [O(k), O(l)]-protocol for DISJ(N, k, l) l If we say that x and y are disjoint then we want to have complete confidence. If we say they intersect, we want to be reasonably certain. l Flip public coins to get a sequence of random subsets of the universe: R 1, R 2, …

x y R 3

x y R 3 y=y∩R 3 y

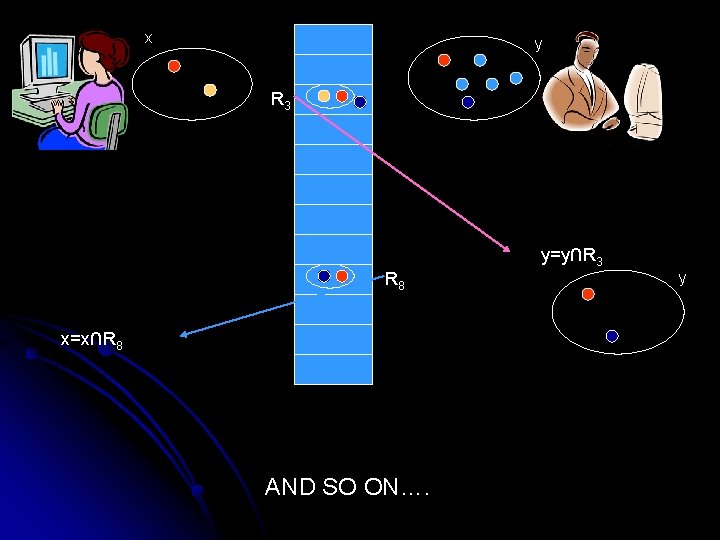
x y R 3 y=y∩R 3 R 8 x=x∩R 8 AND SO ON…. y

A one-sided error randomized [O(k), O(l)]-protocol for DISJ(N, k, l) l We don’t really send the index of R 8, we just send the distance from the last set (83=5). This means that the expected numbers of bits sent by a player is equal to the size of his set l If at some point one of the sets becomes empty, then the originals were disjoint – say so. Otherwise, after a long time, say that there is an intersection.

A one-sided error randomized [O(k), O(l)]-protocol for DISJ(N, k, l) l If x and y were indeed disjoint, the sizes of x and y decrease by a factor of 2 each round. Therefore the total communication is [O(k), O(l)]. l If the sets were disjoint, what is the chance that we say that there is an intersection? Very low.

Fixed-round protocols l If t alternating messages are sent and each message is of size a or b it is called a [t, a, b]-protocol. a b a t b f(x, y)

Static Data Structure Problems l l A static data structure problem is a function f: D Q R D – the data Q – the queries R – Possible answers. Typically, R={0, 1} DS Data query

The Problem MEMBERSHIP(N) INPUT: a set S [N] l QUERIES: of the form “x S? ” l D={S [N]}, |D|=2 N l Q=[N] l R={0, 1} l l The trivial solution is optimal.

The Problem MEMBERSHIP(N, n) INPUT: a set S [N] of size n l QUERIES: of the form “x S? ” l D={S [N] | |S|=n}, |D|=choose(N, n) l Q=[N] l R={0, 1} l

The Cell Probe Model Parameter w – word size l s cells, each containing w bits. l Each query probes at most t cells to get answer l l A query is a decision tree of depth t and degree 2 w

MEMBERSHIP(N, n) Solutions: l Keep every possible answer. s=N, t=1 (better – s=N/w, t=1) l Keep a nonredundant representation. s=log(choose(N, n)), t=log(choose(N, n))

MEMBERSHIP(N, n) Solutions: l Keep a sorted list of all elements. s=nlog(N)/w , t=log(n)*log(N)/w l There is a randomized solution with s=(n/w)c, t=O(1), for some constant c.

What is the connection between Cell Probe and Asymmetric Communication Complexity?

ACC <-> Cell Probe l The communication problem related to a static data structure problem f: D Q {0, 1} if the problem where Alice gets a query, Bob gets the data, and they should decide if this is a “yes” instance or a “no” instance

Communication Problem MEM(N, n) l Alice gets x [N], Bob gets y [N], |y|=n, they should decide if x y. l Trivial protocols: [1, nlog. N] , [log. N, 1]

Lemma CP->AAC If there is a solution to the data structure problem with word size w taking s cells and with query time t, then there is a [2 t, log(s), w]-protocol for the communication problem Therefore a lower bound on ACC gives us a lower bound on Cell Probe

Finer points of CP->AAC How is the communication complexity model stronger than the Cell Probe Model? l Answer: In its adaptivity l Which form of Cell Probe lower bounds can we get from the CP->AAC Lemma? l Answer: the bound on space is up to a polynomial l

Restricted AAC->CP If there is a [O(1), a, b]-protocol for the communication problem then the data structure problem has a solution with word size w=b, t=O(1) and s=2 O(a) Proof: The Data Structure for input y contains the message Bob should send next for every possible history of messages Alice can send, for any query.

Lower Bounding The Communication Complexity

Communication Problem MEM(N, l) l Alice gets x [N], Bob gets y [N], |y|=l, they should decide if x y. l NONMEM(N, l) is the same problem, when Alice and Bob want to decide if x y l Trivial protocols: [1, l*log. N] , [log. N, 1]

Problem <-> Matrix l We identify a communication problem f: X×Y {0, 1} with a |X|×|Y| Matrix where M[x][y]=f(x, y). l The matrix of NONMEM(N, l) has N rows and columns. Each column has N-l 1 entries

Problem <-> Matrix l A problem (matrix) is (u, v)-rich if at least v columns contain at least u 1 -entries. (4, 3)-rich l NONMEM(N, l) is (N-l, )-rich.

The Richness Lemma l 1. 2. l Let f be a communication problem that: is (u, v)-rich has a randomized one-sided error [a, b]protocol. Then f contains a u/2 a+2 over v/2 a+b+2 submatrix of 1 -entries.

Randomized Lower Bound for MEM(N, l) l Say MEM(N, l) has a negative-one-sided error [a, b]-protocol. Let a<log(l), l<N/2. l Then NONMEM(N, l) has a one-sided error [a, b]-protocol

Randomized Lower Bound for NONMEM(N, l) l NONMEM(N, l) is (N-l, )-rich l Therefore it has a 1 -submatrix of dimensions at least (N-l)/2 a+2 over /2 a+b+2

Randomized Lower Bound for NONMEM(N, l) l However, if there is a 1 -submatrix of dimensions r on s then s≤ l By substituting for s and r, simplifying and bounding we get 2 a(a+b)=Ω(l)

Randomized [O(a), O(l/2 a)] Upper Bound for NONMEM(N, l) On the other hand, NONMEM(N, l) has a [O(a), O(l/2 a)]-protocol, for all a<log(l): l Alice sends Bob the first a indices of R’s that contain x. This allows Bob to reduce y to expected size l/2 a. l Then Bob sends a couple indices that contain y. l If we are not yet sure that they are disjoint, we say that they intersect. l

Tightness for NONMEM(N, l) l NONMEM(N, l) has a [O(a), O(l/2 a)]-protocol, for all a<log(l) l 2 a(a+b)= 2 a(a+l/2 a)=? O(l) Therefore the last result is tight? l There are constants c, c’>0, so that for any a, b=l/2 ca is enough. b=l/2 c’a is not enough. l l

The Richness Lemma l 1. 2. l Let f be a communication problem that: is (u, v)-rich has a randomized one-sided error [a, b]protocol. Then f contains a u/2 a+2 over v/2 a+b+2 submatrix of 1 -entries.

Proof of the Richness Lemma l First let us prove a weaker result: if f has a deterministic [a, b]-protocol then it contains a u/2 a over v/2 a+b submatrix of 1 -entries. l We prove this by induction on a+b:

Proof of the Richness Lemma For a+b=0 – |X|≥u, |Y|≥v, and f(x, y)=1 for all x, y, so this is trivial. l Now, if Alice send the first bit: l X 0 – inputs for which she sends 0 l X 1 – inputs for which she sends 1 l Let f 0, f 1 be the restrictions of f to X 0 Y, X 1 Y. l

Proof of the Richness Lemma At least one of them is (u/2, v/2)-rich, and both have a [a-1, b] protocol. l By the induction it contains a (u/2)/2 a-1 over (v/2)/2 a+b-1 1 -submatrix. l In the other case, Bob send the first bit. l Define Y 0, Y 1, f 0, f 1. At least one of them is (u, v/2)-rich, and proceed similarly. l

Proof of the Richness Lemma Now let us prove the general case: l Let S be the set of u*v rich-positions in the matrix l Let us look at some coin-flip sequence. l

Proof of the Richness Lemma Let X = #{1 s in S} l E[X]>=2/3 * uv l => There exists such a sequence for which X>=2/3 * uv l l Fix the sequence, to get a deterministic algorithm. This algorithm computes a function f’ that is close to f.

Proof of the Richness Lemma l By a counting argument, f’ is (u/4, v/4)-rich, and so it has a 1 -submatrix of the required size ( u/2 a+2 over v/2 a+b+2 ) l This is a 1 -submatrix in f too, because the error is one-sided. l Q. E. D.

A Richness Results for two-sided error l Let d, e>0, and let f: X×Y {0, 1} be a communication problem with at least a dfraction of 1 s. If f has a randomized twosided error [a, b]-protocol then f has a submatrix M of dimensions at least |X|/2 O(a) over |Y|/2 O(a+b) with at least a (1 -e)fraction of 1 s.

The SPAN(n) Problem In SPAN, Alice gets x {0, 1}n and Bob gets a vector subspace y {0, 1}n l y can be represented using a basis of k≤n vectors – O(n 2) bits l Alice and Bob must decide if x∈y. l l Trivial Protocols: [n, 1] , [1, n 2]

Lower bounds for SPAN l l l 1. 2. Let’s prove that in any [a, b] randomized one-sided error protocol for SPAN, either a=Ω(n), or b=Ω(n 2) We will assume that y is of dimension n/2. We will prove that: 2/4 n/2 n SPAN is (2 , 2 )-rich, and SPAN does not contain a 1 -submatrix 2/12 n/3 n of dimensions 2 over 2

SPAN is 2/4 n/2 n (2 , 2 )-rich Each subspace contains exactly 2 n/2 vectors => each column contains 2 n/2 1 s. l How many subspaces of dimension n/2 are there? l Lets choose a basis: we have 2 n-1 possibilities for the first vector, 2 n-2 for the second, 2 n-4 for the third, etc. l

SPAN is 2/4 n/2 n (2 , 2 )-rich We chose each basis (n/2)! times l How many basis does a subspace has? l We have 2 n/2 -1 options to choose the first vector, 2 n/2 -2 for the second, etc. l We again chose each basis (n/2)! times. l l Thus, there at least dimension n/2. 2/4 n 2 subspaces of

SPAN does not contain a 1 -submatrix 2/12 n/3 n of dimensions 2 over 2 Lets look at a 1 -submatrix with at least 2 n/3 rows. The subspace spanned by them is of dimension at least n/3. l How many subspaces of dimension n/2 can include this entire subspace? l 2/12 n l 2 l And we’re done.

The Round Elimination Lemma

f->Pm(f) l Let f: X×Y->{0, 1} be a communication problem l l Pm(f) is: Alice gets m elements from X, x 1, …, xm Bob gets 1≤i≤m, y Y and also x 1, …, xi-1 They want to compute f(xi, y) l How meaningful can Alice’s first message be? l l

The Round Elimination Lemma Let C=99, R=4256. l Say that PRa(f) has a randomized twosided error [t, a, b]-protocol in which Alice sends the first message. l Then there is a randomized two-sided error [t-1, Ca, Cb]-protocol with Bob sending the first message. l

General framework for LB proofs using the Round Elimination Lemma [t, a, b]-protocol for F(n) [t, a, b]-protocol for Pm(F(n’)) (typically n’=n/m) [t-1, Ca, Cb]-protocol for F(n’) [1, Ct-1 a, Ct-1 b]-protocol for F(n(t-1))

The problem GT(n) Alice and Bob each gets an n-bit integer. l They want to decide if x<y. l x y x<y?

The problem GT(n) Deterministic communication complexity is linear l Randomized comm. complexity with twosided error is O(logn) (using a logarithmic number of rounds) l l When limited to t rounds: There is a [t, n 1/tlogn]-protocol

GT(n) does not have a [t, n 1/t. C-t]-protocol l Theorem: Let C=99. There does not exist a randomized twosided error [t, n 1/t. C-t]-protocol for GT(n)

GT(n) does not have a [t, n 1/t. C-t]-protocol l By induction on t Say there was a [t, n 1/t. C-t]-protocol for GT(n). l Then there is a [t, n 1/t. C-t]-protocol for Pm(GT(n’)) for m=n 1/t, n’=n(t-1)/t l From the round Elimination Lemma, there is a [t-1, n 1/t. C-(t-1)]-protocol for GT(n’). Contradiction. l

GT(n) does not have a [t, n 1/t. C-t, n 1/t. C-t]-protocol for GT(n) [t, n 1/t. C-t]-protocol for Pm(GT(n’)) for m=n 1/t, n’=n(t-1)/t l l l Alice constructs a n-bit integer x’: She concatenates x 1…xm Bob constructs a n-bit integer y’: He concatenates x 1…xi-1 then y and the rest is 1 s We get x’>y’ xi>y

THE END