Astronomical Spectroscopy Notes from Richard Gray Appalachian State

Astronomical Spectroscopy Notes from Richard Gray, Appalachian State, and D. J. Schroeder 1974 in “Methods of Experimental Physics, Vol. 12 -Part A Optical and Infrared”, p. 463. See also Chapter 3 in “Stellar Photospheres” textbook Elements Resolution Grating Equation Designs 1

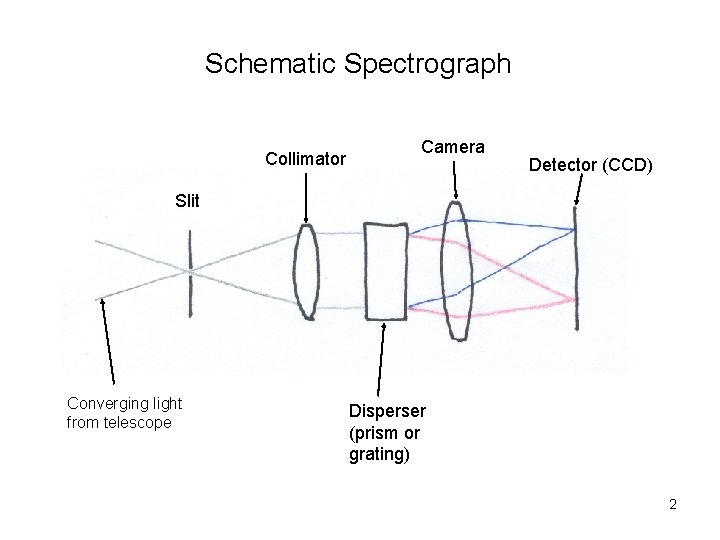
Schematic Spectrograph Collimator Camera Detector (CCD) Slit Converging light from telescope Disperser (prism or grating) 2

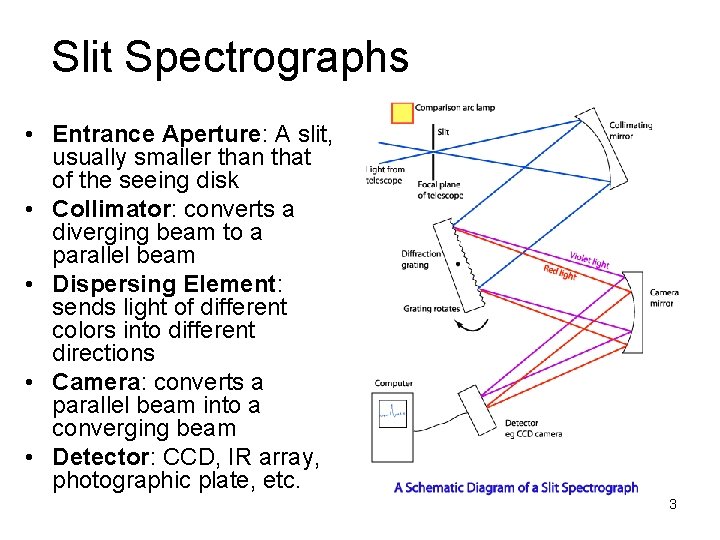
Slit Spectrographs • Entrance Aperture: A slit, usually smaller than that of the seeing disk • Collimator: converts a diverging beam to a parallel beam • Dispersing Element: sends light of different colors into different directions • Camera: converts a parallel beam into a converging beam • Detector: CCD, IR array, photographic plate, etc. 3

Why use a slit? 1) A slit fixes the resolution, so that it does not depend on the seeing. 2) A slit helps to exclude other objects in the field of view A spectrograph should be designed so that the slit width is approximately the same as the average seeing. Otherwise you will lose a lot of light. 4

Design Considerations: Resolution vs Throughput Without the disperser, the spectrograph optics would simply reimage the slit on the detector. With the disperser, monochromatic light passing through the spectrograph would result in a single slit image on the detector; its position on the detector is determined by the wavelength of the light. This implies a spectrum is made up of overlapping images of the slit. A wide slit lets in a lot of light, but results in poor resolution. A narrow slit lets in limited light, but results in better resolution. 5

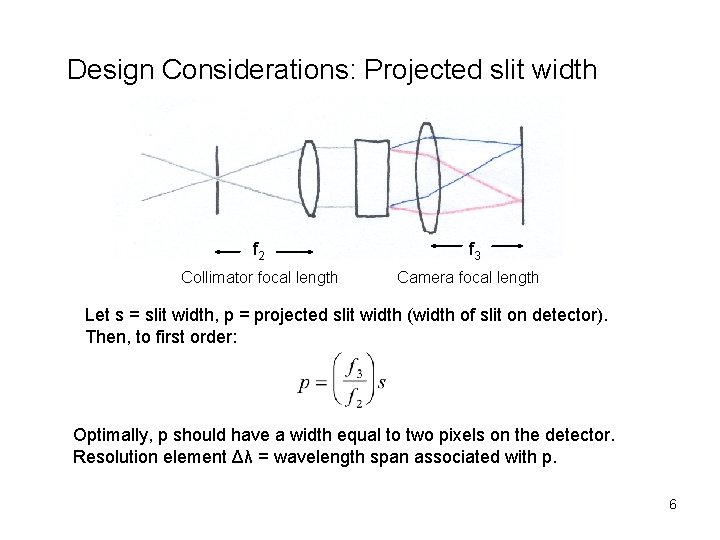
Design Considerations: Projected slit width f 2 Collimator focal length f 3 Camera focal length Let s = slit width, p = projected slit width (width of slit on detector). Then, to first order: Optimally, p should have a width equal to two pixels on the detector. Resolution element Δλ = wavelength span associated with p. 6

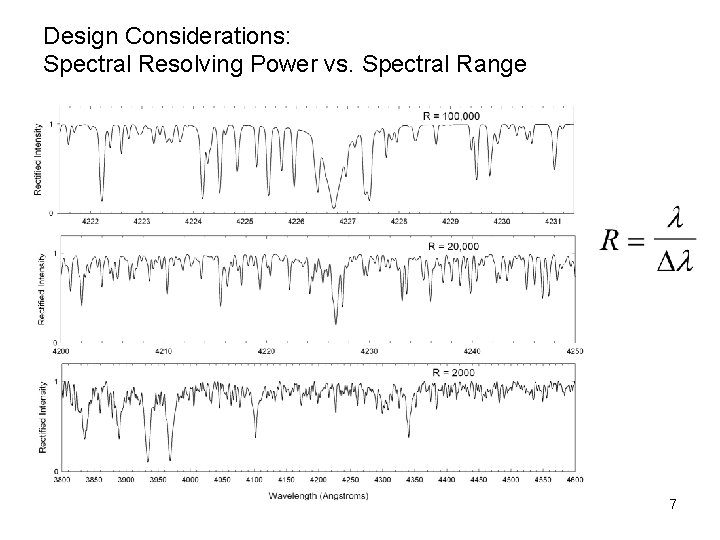
Design Considerations: Spectral Resolving Power vs. Spectral Range 7

Dispersers Prisms: disperse light into a spectrum because the index of refraction is a function of the wavelength. Usually: n(blue) > n(red). Diffraction gratings: work through the interference of light. Most modern spectrographs use diffraction gratings. Most astronomical spectrographs use reflection gratings instead of transmission gratings. A combination of the two is called a Grism. 8

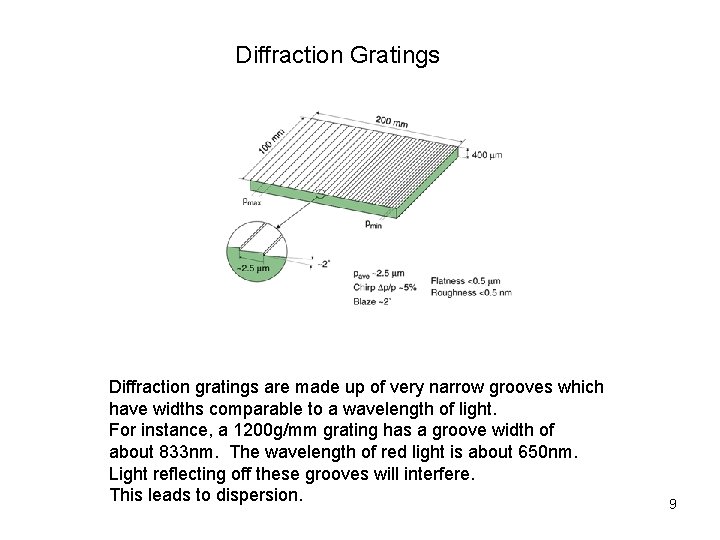
Diffraction Gratings Diffraction gratings are made up of very narrow grooves which have widths comparable to a wavelength of light. For instance, a 1200 g/mm grating has a groove width of about 833 nm. The wavelength of red light is about 650 nm. Light reflecting off these grooves will interfere. This leads to dispersion. 9

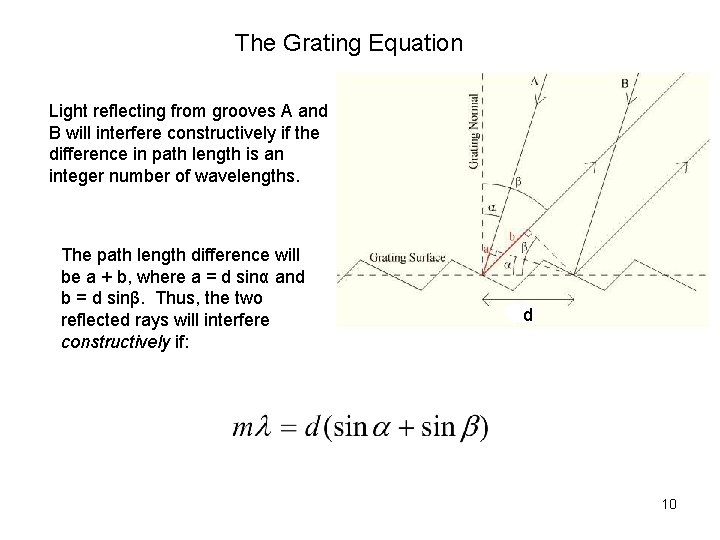
The Grating Equation Light reflecting from grooves A and B will interfere constructively if the difference in path length is an integer number of wavelengths. The path length difference will be a + b, where a = d sinα and b = d sinβ. Thus, the two reflected rays will interfere constructively if: d 10

Meaning: Let m = 1. If a ray of light of wavelength λ strikes a grating of groove spacing d at an angle α with the grating normal, it will be diffracted at an angle β from the grating. If m, d and α are kept constant, λ is clearly a function of β. Thus, we have dispersion. 11

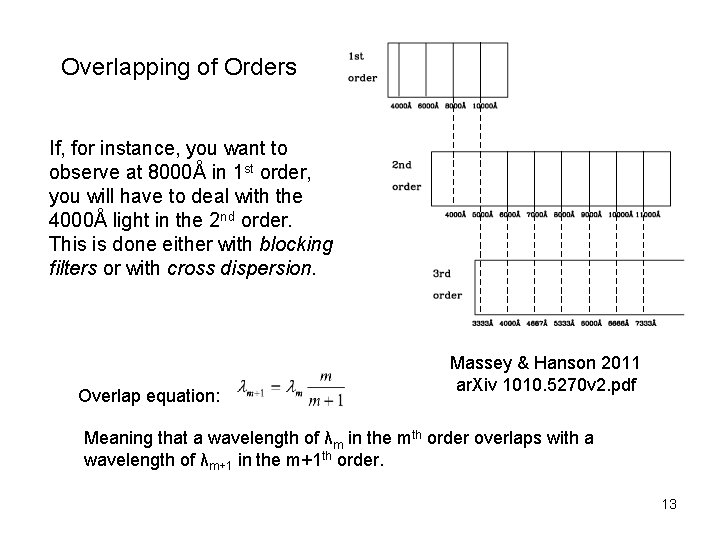
m is called the order of the spectrum. Thus, diffraction gratings produce multiple spectra. If m = 0, we have the zeroth order, undispersed image of the slit. If m = 1, we have two first order spectra on either side of the m = 0 image, etc. Diffraction grating illustrated is a transmission grating. These orders will overlap, which produces problems for grating spectrographs. 12

Overlapping of Orders If, for instance, you want to observe at 8000Å in 1 st order, you will have to deal with the 4000Å light in the 2 nd order. This is done either with blocking filters or with cross dispersion. Overlap equation: Massey & Hanson 2011 ar. Xiv 1010. 5270 v 2. pdf Meaning that a wavelength of λm in the mth order overlaps with a wavelength of λm+1 in the m+1 th order. 13

14

Dispersion & Resolving Power Dispersion is the degree to which the spectrum is spread out. To get high resolution, it is really necessary to use a diffraction grating that has high dispersion. Dispersion (dβ/dλ) is given by: Thus, to get high resolution, three strategies are possible: long camera focal length (f 3), high order (m), or small grating spacing (d). The last has some limitations. The first two lead to the two basic designs for high-resolution spectrographs: coudé (long f 3) and echelle (high m). 15

Grating Spectrographs • Reciprocal dispersion P=(d cosβ)/(mf 3) (often quoted in units of Å/mm) • Free spectral range m(λ+Δλ)=(m+1)λ Δλ=λ/m λ difference between two orders at same β • Blaze angle with max. intensity where angle of incidence = angle of reflection 16

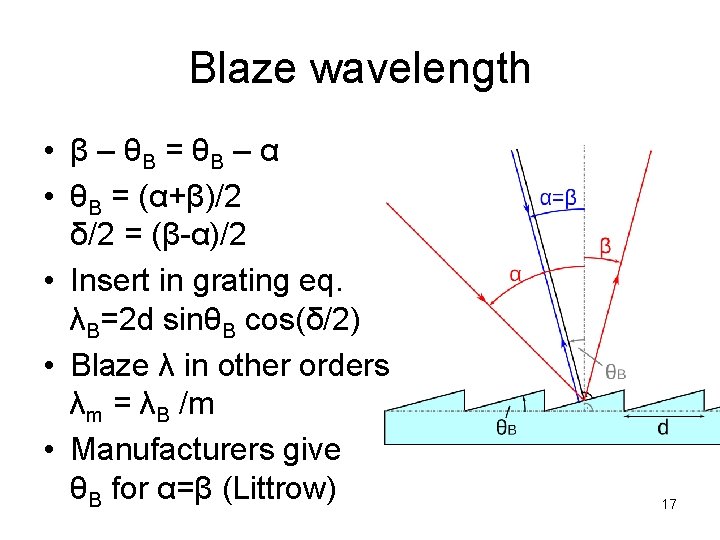
Blaze wavelength • β – θB = θB – α • θB = (α+β)/2 δ/2 = (β-α)/2 • Insert in grating eq. λB=2 d sinθB cos(δ/2) • Blaze λ in other orders λm = λB /m • Manufacturers give θB for α=β (Littrow) 17

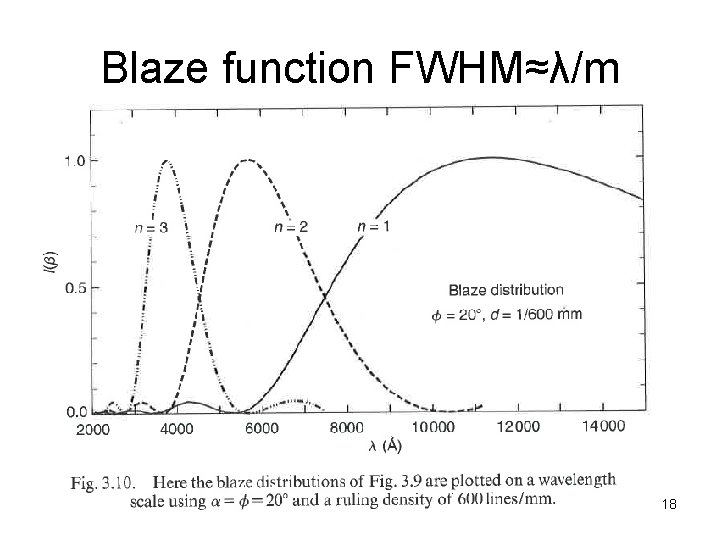
Blaze function FWHM≈λ/m 18

Three basic optical designs for spectrographs Littrow (not commonly used in astronomy). Ebert: used in astronomy, but p = s. Note camera = collimator. Czerny-Turner: most versatile design. Most commonly used in astronomy. 19

High-resolution spectrographs: KPNO Coude Feed 20

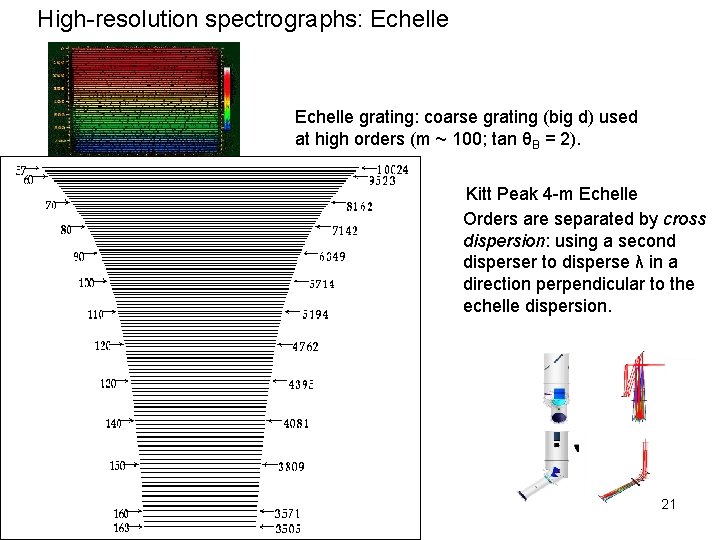
High-resolution spectrographs: Echelle grating: coarse grating (big d) used at high orders (m ~ 100; tan θB = 2). Kitt Peak 4 -m Echelle Orders are separated by cross dispersion: using a second disperser to disperse λ in a direction perpendicular to the echelle dispersion. 21

Hamilton echelle spectrum format: Vogt 1987, PASP, 99, 1214 m λ 22

CHIRON, 1. 5 m CTIO R=27, 000 to 80, 000 23

ARC Echelle Spectrograph 3. 5 telescope, Apache Point R = 33, 000 24