Associative Memory by Recurrent Neural Networks with Delay

Associative Memory by Recurrent Neural Networks with Delay Elements Seiji MIYOSHI Hiro-Fumi YANAI Kobe City College of Tech. JAPAN Ibaraki Univ. 　 Masato OKADA RIKEN BSI , ERATO KDB JAPAN miyoshi@kobe-kosen. ac. jp www. kobe-kosen. ac. jp/~miyoshi/ JAPAN 　　　

Background • Synapses of real neural systems seem to have delays. • It is very important to analyze associative memory model with delayed synapses. • Computer simulation is powerful method. However, There is a Limit on the number of neurons. Simulating network with large delay steps is realistically impossible. • Theoretical and analytical approach is indispensable to research on delayed networks. • Yanai-Kim theory by using Statistical Neurodynamics Good Agreement with computer simulation Computational Complexity is O(L 4 t)

Objective • To derive macroscopic steady state equations by using discrete Fourier transformation • To discuss storage capacity quantitatively even for a large L limit (L: length of delay)

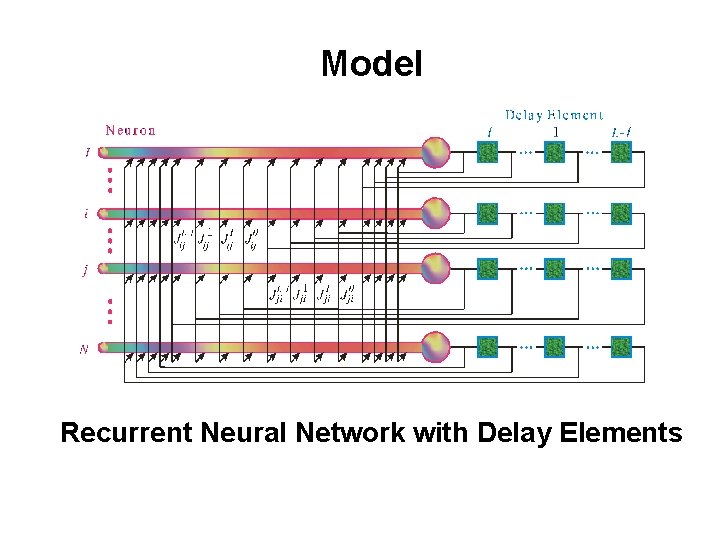
Model Recurrent Neural Network with Delay Elements

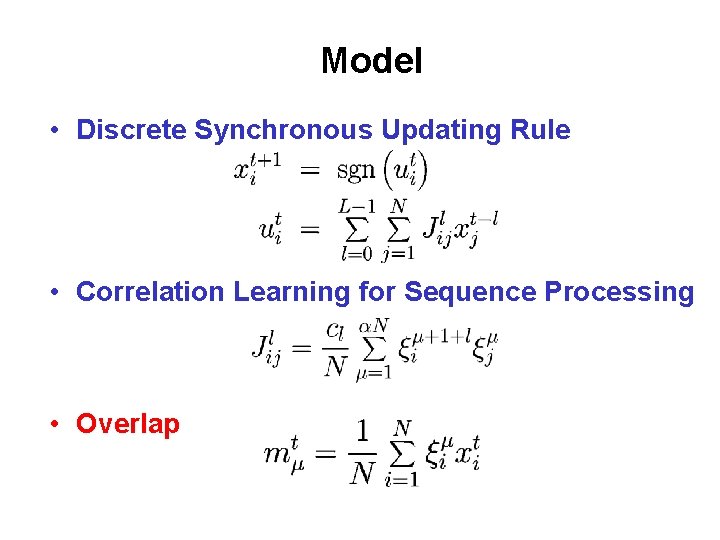
Model • Discrete Synchronous Updating Rule • Correlation Learning for Sequence Processing • Overlap

Macrodynamical Equations by Statistical Neurodynamics Yanai & Kim(1995)　 Miyoshi, Yanai & Okada(2002)

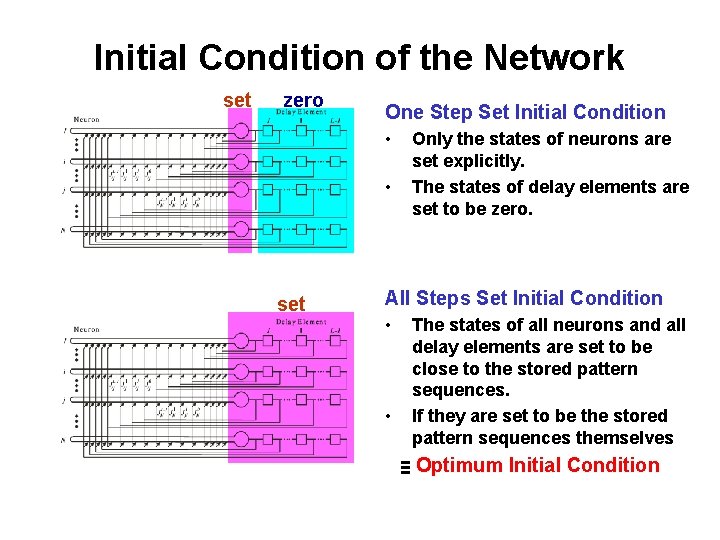
Initial Condition of the Network set zero One Step Set Initial Condition • • set Only the states of neurons are set explicitly. The states of delay elements are set to be zero. All Steps Set Initial Condition • • The states of all neurons and all delay elements are set to be close to the stored pattern sequences. If they are set to be the stored pattern sequences themselves ≡ Optimum Initial Condition

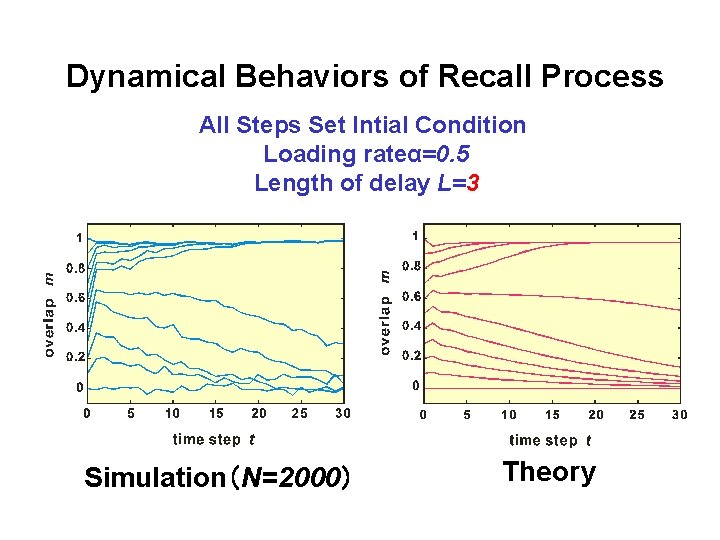
Dynamical Behaviors of Recall Process All Steps Set Intial Condition Loading rateα=0. 5 Length of delay L=3 Simulation（N=2000） Theory

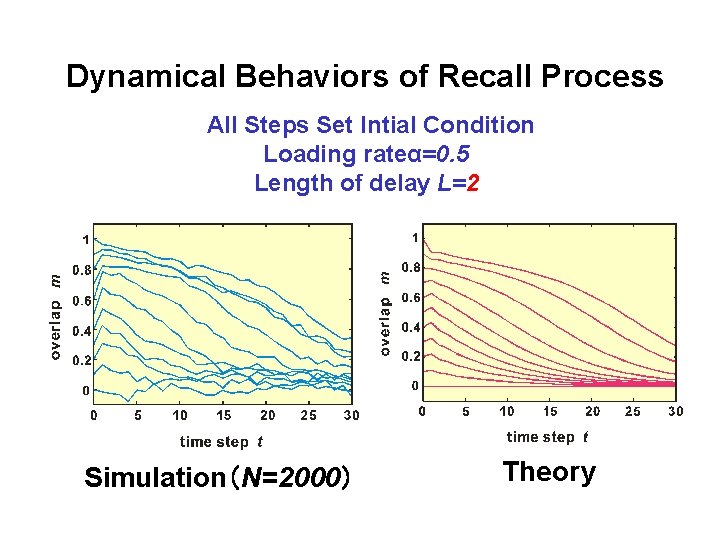
Dynamical Behaviors of Recall Process 　All Steps Set Intial Condition Loading rateα=0. 5 Length of delay L=2 Simulation（N=2000） Theory

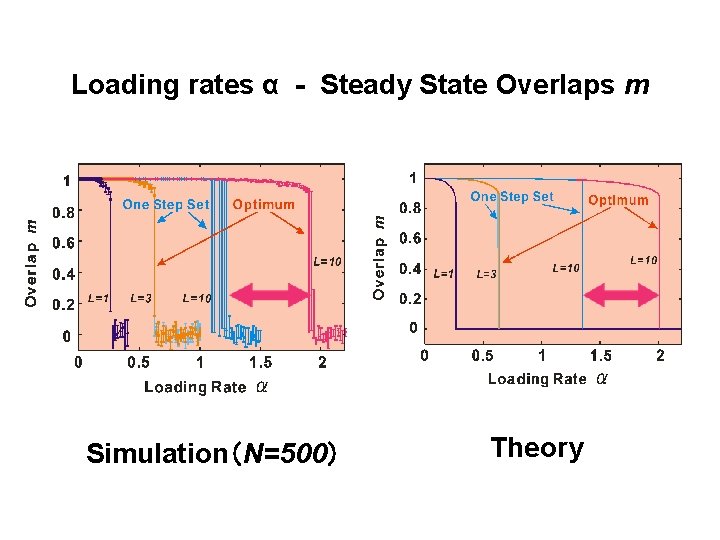
Loading rates α - Steady State Overlaps m Simulation（N=500） Theory

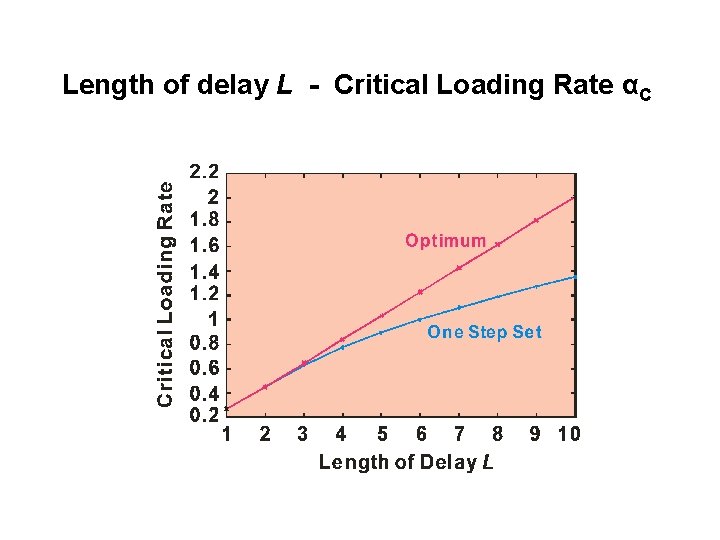
Length of delay L - Critical Loading Rate αC

Macrodynamical Equations by Statistical Neurodynamics Yanai & Kim(1995)　 Miyoshi, Yanai & Okada(2002) • Good Agreement with Computer Simulation • Computational Complexity is O(L 4 t)

Macroscopic Steady State Equations • Accounting for Steady State • Parallel Symmetry in terms of Time Steps • Discrete Fourier Transformation

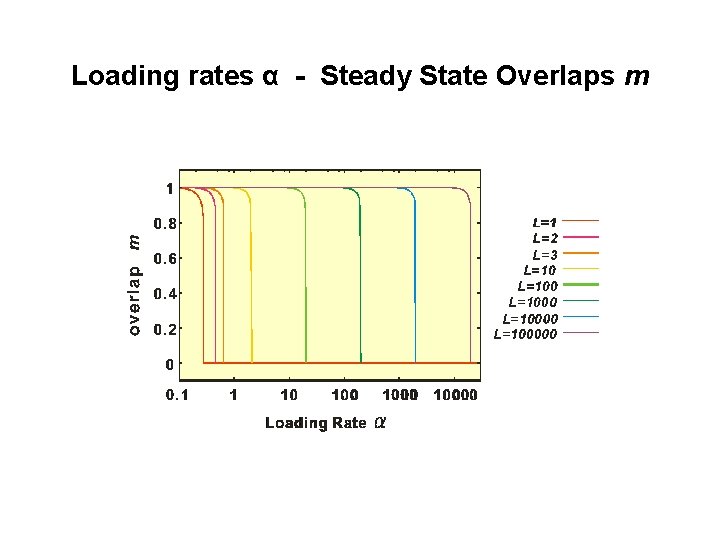
Loading rates α - Steady State Overlaps m

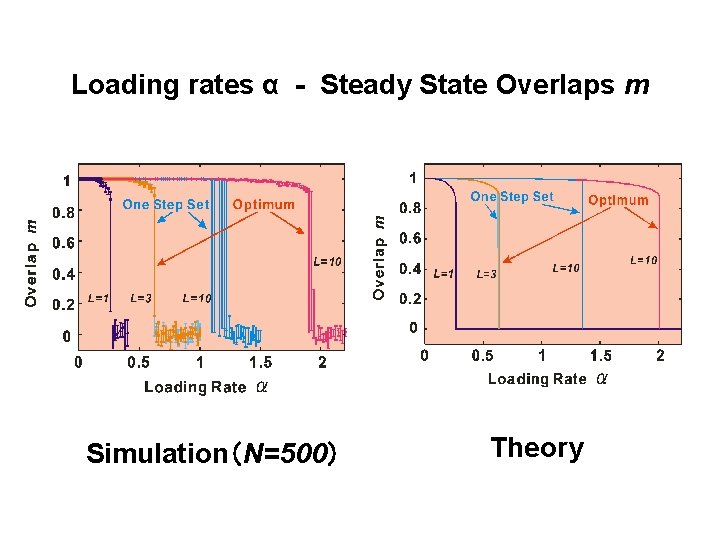
Loading rates α - Steady State Overlaps m Simulation（N=500） Theory

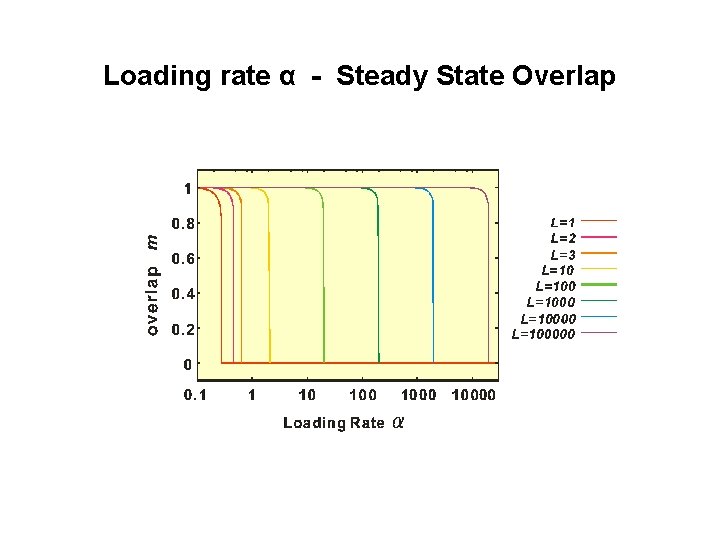
Loading rate α - Steady State Overlap

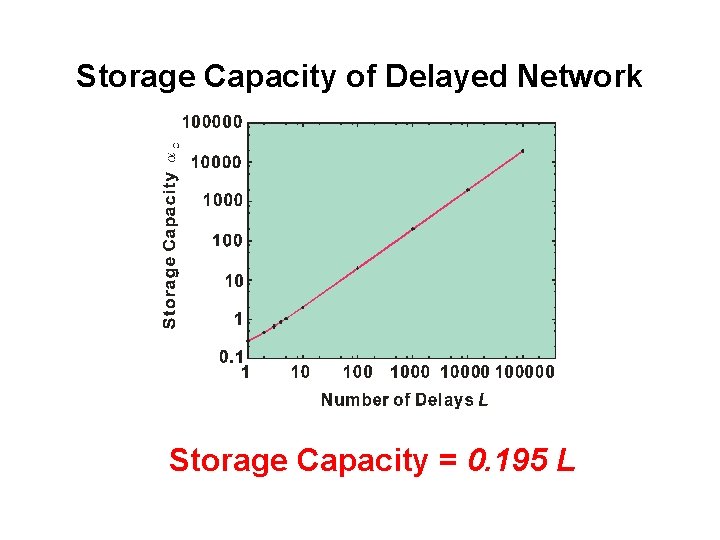
Storage Capacity of Delayed Network Storage Capacity = 0. 195 L

Conclusions • Yanai-Kim theory (macrodynamical equations for delayed network) is re-derived. → Computational Complexity is O(L 4 t) → Intractable to discuss macroscopic properties in a large L limit • Steady state equations are derived by using discrete Fourier transformation. → Computational complexity does not formally depend on L → Phase transition points agree with those under the optimum initial conditions, that is, the Storage Capacities ! • Storage capacity is 0. 195 L in a large L limit.