Associative Memories A Morphological Approach Outline n Associative

Associative Memories A Morphological Approach

Outline n Associative Memories n Motivation n Capacity Vs. Robustness Challenges n Morphological Memories n Improving Limitations n Experiment n Results n Summary n References

Associative Memories n Motivation n Human ability to retrieve information from applied associated stimuli n n n Ex. Recalling one’s relationship with another after not seeing them for several years despite the other’s physical changes (aging, facial hair, etc. ) Enhances human awareness and deduction skills and efficiently organizes vast amounts of information Why not replicate this ability with computers? n Ability would be a crucial addition to the Artificial Intelligence Community in developing rational, goal oriented, problem solving agents n One realization of Associative Memories are Contents Addressable Memories (CAM)

Capacity versus Robustness Challenge for Associative Memories n In early memory models, capacity was limited to the length of the memory and allowed for negligible input distortion (old CAMs). n Ex. Linear Associative Memory n Recent years have increased the memory’s robustness, but sacrificed capacity n J. J. Hopfield’s proposed Hopfield Network n Capacity: , where n is the memory length n Current research offers a solution which maximizes memory capacity while still allowing for input distortion n Morphological Neural Model n n n Capacity: essentially limitless (2 n in the binary case) Allows for Input Distortion One Step Convergence

Morphological Memories n Formulated using Mathematical Morphology Techniques n Image Dilation n Image Erosion n Training Constructs Two Memories: M and W n M used for recalling dilated patterns n W used for recalling eroded patterns n M and W are not sufficient…Why? n General distorted patterns are both dilated and eroded n solution: hybrid approach n Incorporate a kernel matrix, Z, into M and W n General distorted pattern recall is now possible! n Input → MZ → WZ → Output

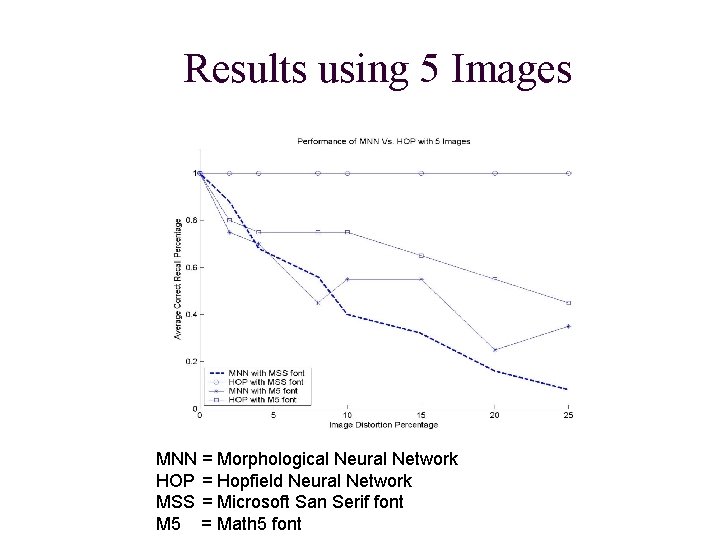
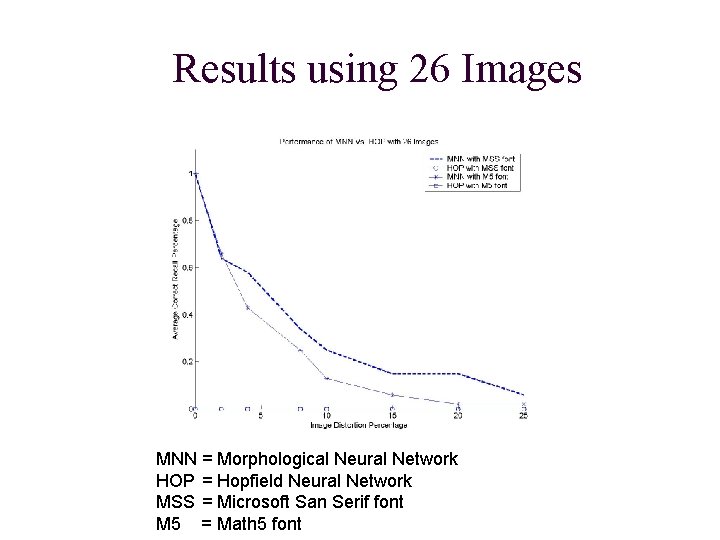
Improving Limitations n Experiment n Construct a binary morphological auto-associative memory to recall bitmap images of capital alphabetic letters n Use Hopfield Model for baseline n Construct letters using Microsoft San Serif font (block letters) and Math 5 font (cursive letters) n Attempt recall 5 times for each pattern for each image distortion at 0%, 2%, 4%, 8%, 10%, 15%, 20%, and 25% n Use different memory sizes: 5 images, 10, 26, and 52 n Use Average Recall Rate per memory size as a performance measure, where recall is correct if and only if it is perfect

Results n Morphological Model and Hopfield Model: n Both degraded in performance as memory size increased n Both recalled letters in Microsoft San Serif font better than Math 5 font n Morphological Model: n Always perfect recall with 0% image distortion n Performance smoothly degraded as memory size and distortion increased n Hopfield Model: n Never correctly recalled images when memory contained more than 5 images

Results using 5 Images MNN = Morphological Neural Network HOP = Hopfield Neural Network MSS = Microsoft San Serif font M 5 = Math 5 font

Results using 26 Images MNN = Morphological Neural Network HOP = Hopfield Neural Network MSS = Microsoft San Serif font M 5 = Math 5 font

Summary n The ability for humans to retrieve information from associated stimuli continues to elicit great interest among researchers n Progress Continues with the development of enhanced neural models n Linear Associative Memory → Hopfield Model → Morphological Model n Using Morphological Model n Essentially Limitless Capacity n Guaranteed Perfect Recall with Undistorted Input n One Step Convergence

References n Y. H. Hu. Associative Learning and Principal Component Analysis. Lecture 6 Notes, 2003 n R. P. Lippmann. An Introduction to Computing with Neural Nets. IEEE Transactions of Acoustics, Speech, and Signal Processing, -4: 4 - 22, 1987. ASSP n R. Mc. Eliece and et. Al. The Capacity of Hopfield Associative Memory. Transactions of Information Theory, 1: 33 -45, 1987. n G. X. Ritter and P. Sussner. An Introduction to Morphological Neural Networks. In Proceedings of the 13 th International Conference on Pattern Recognition, pages 709 -711, Vienna, Austria, 1996. n G. X. Ritter, P. Sussner, and J. L. Diaz de Leon. Morphological Associative Memories. IEEE Transactions on Neural Networks, 9(2): 281 -293, March 1998.