Association Rules Apriori Algorithm 1 Computation Model u

Association Rules Apriori Algorithm 1

Computation Model u Typically, data is kept in a flat file rather than a database system. w Stored on disk. w Stored basket by basket. u The true cost of mining disk resident data is usually the number of disk I/O’s. u In practice, association rule algorithms read the data in passes – all baskets read in turn. u Thus, we measure the cost by the number of passes an algorithm takes. Item Item Item Basket 1 Basket 2 Basket 3 Etc. 2

Main Memory Bottleneck u. For many frequent itemset algorithms, main memory is the critical resource. w As we read baskets, we need to count something, e. g. , occurrences of pairs. w The number of different things we can count is limited by main memory. w Swapping counts in/out is a disaster. 3

Finding Frequent Pairs u. The hardest problem often turns out to be finding the frequent pairs. u. We’ll concentrate on how to do that, then discuss extensions to finding frequent triples, etc. 4

Naïve Algorithm u. Read file once, counting in main memory the occurrences of each pair. w From each basket of n items, generate its n (n 1)/2 pairs by two nested loops. u. Fails if (#items)2 exceeds main memory. w Remember: #items can be 100 K (Wal Mart) or 10 B (Web pages). 5

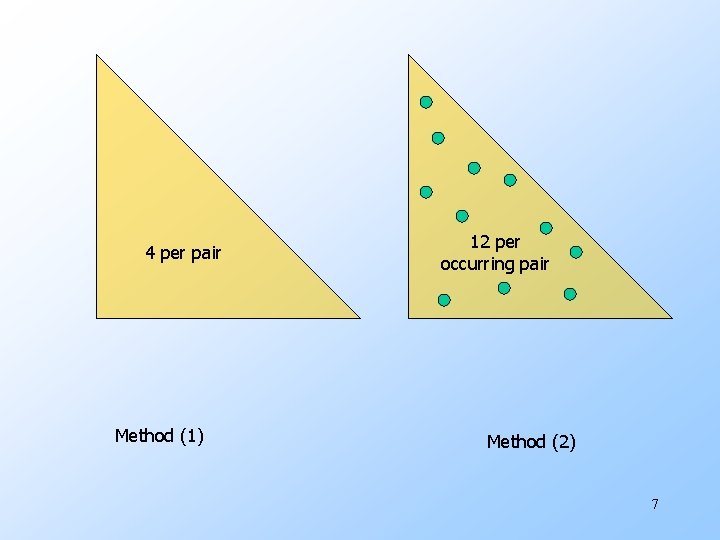
Details of Main Memory Counting u Two approaches: 1. Count all pairs, using a triangular matrix. 2. Keep a table of triples [i, j, c] = the count of the pair of items {i, j } is c. u (1) requires only 4 bytes/pair. w Note: assume integers are 4 bytes. u (2) requires 12 bytes, but only for those pairs with count > 0. 6

4 per pair Method (1) 12 per occurring pair Method (2) 7

Triangular Matrix Approach – (1) u. Number items 1, 2, …, n u. Requires table of size O(n). u. Count {i, j } only if i < j. u. Keep pairs in the order w w w {1, 2}, {1, 3}, …, {1, n}, {2, 3}, {2, 4}, …, {2, n}, {3, 4}, …, {3, n}, … {n 1, n}. 8

Triangular Matrix Approach – (2) u. Let n be the number of items. Find pair {i, j } at the position (i 1)n i(i+1)/2+j {1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4} {3, 4} u. Total number of pairs n (n – 1)/2; total bytes about 2 n 2. 9

Details of Approach #2 u. Total bytes used is about 12 p, where p is the number of pairs that actually occur. w Beats triangular matrix if at most 1/3 of possible pairs actually occur. u. May require extra space for retrieval structure, e. g. , a hash table. 10

Apriori Algorithm for pairs– (1) u. A two pass approach called a-priori limits the need for main memory. u. Key idea: monotonicity : if a set of items appears at least s times, so does every subset. w Contrapositive for pairs: if item i does not appear in s baskets, then no pair including i can appear in s baskets. 11

Apriori Algorithm for pairs– (2) u Pass 1: Read baskets and count in main memory the occurrences of each item. Item counts Frequent items w Requires only memory proportional to #items. u Pass 2: Read baskets again and count in main memory only those pairs whose both elements were found in Pass 1 to be frequent. Counts of candidate pairs Pass 1 Pass 2 w Requires memory proportional to square of frequent items only. 12

Detail for A Priori u. You can use the triangular matrix method with n = number of frequent items. w Saves space compared with storing triples. u. Trick: number frequent items 1, 2, … and keep a table relating new numbers to original item numbers. 13

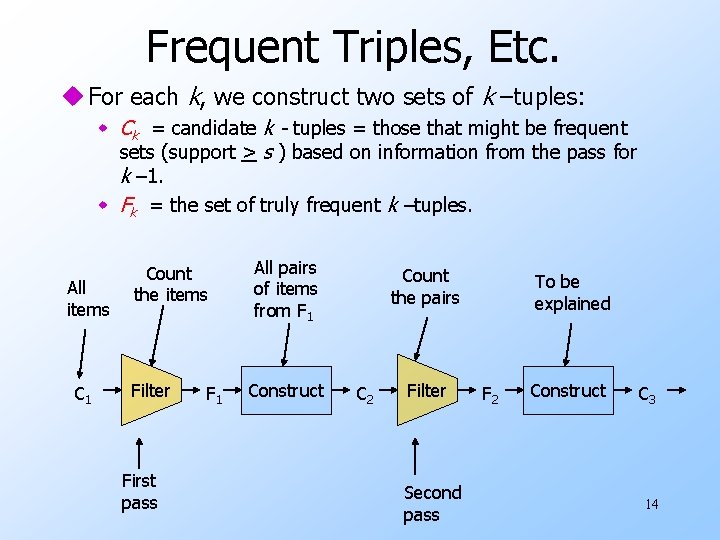
Frequent Triples, Etc. u For each k, we construct two sets of k –tuples: w Ck = candidate k - tuples = those that might be frequent sets (support > s ) based on information from the pass for k – 1. w Fk = the set of truly frequent k –tuples. All items C 1 Count the items Filter First pass F 1 All pairs of items from F 1 Construct Count the pairs C 2 Filter Second pass To be explained F 2 Construct C 3 14

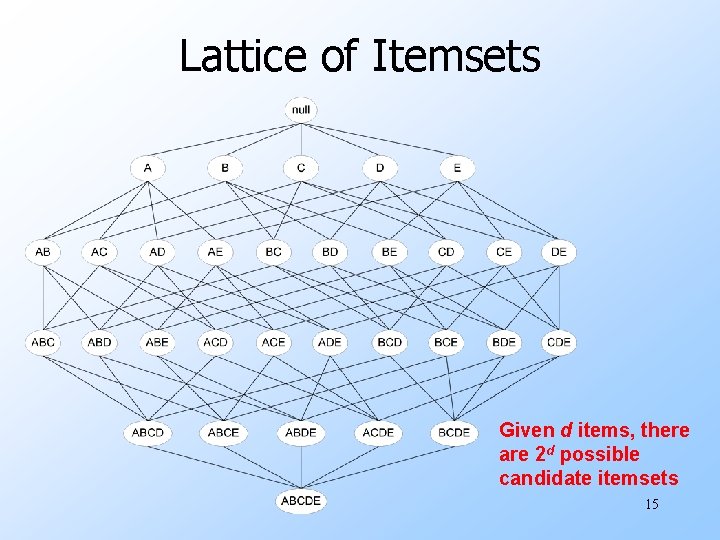
Lattice of Itemsets Given d items, there are 2 d possible candidate itemsets 15

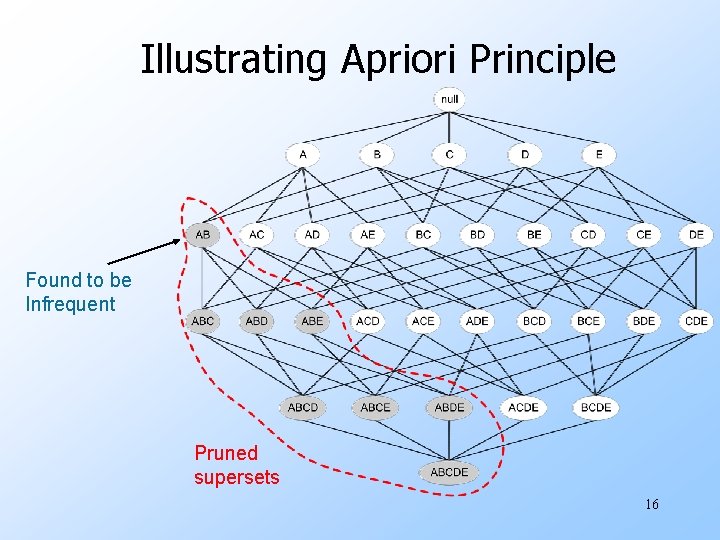
Illustrating Apriori Principle Found to be Infrequent Pruned supersets 16

Full Apriori Algorithm w Let k=1 w Generate frequent itemsets of length 1 w Repeat until no new frequent itemsets are found k=k+1 1. Generate length k candidate itemsets from length k 1 frequent itemsets 2. Prune candidate itemsets containing subsets of length k 1 that are infrequent 3. Count the support of each candidate by scanning the DB and eliminate candidates that are infrequent, leaving only those that are frequent 17

Candidate generation An effective candidate generation procedure: 1. Should avoid generating too many unnecessary candidates. 2. Must ensure that the candidate set is complete, 3. Should not generate the same candidate itemset more than once. 18

Data Set Example s=3 19

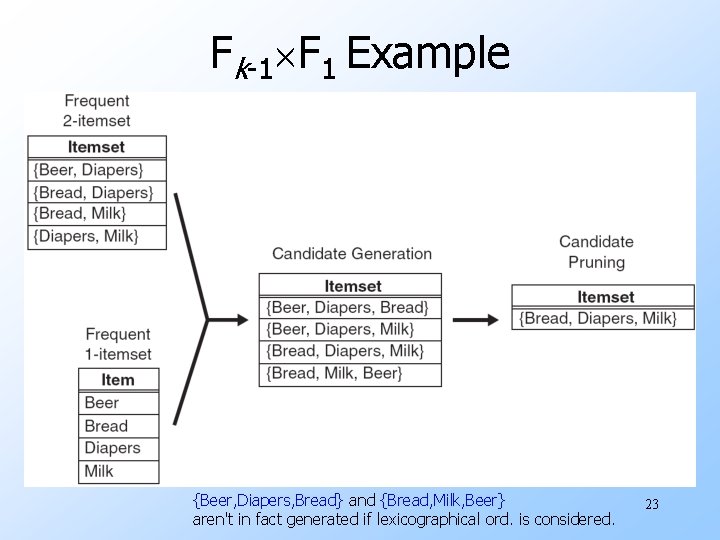
Fk 1 F 1 Method u Extend each frequent (k 1) itemset with a frequent 1 itemset. u Is it complete? u Yes, because every frequent k itemset is composed of w a frequent (k-1) itemset and w a frequent 1 itemset. u However, it doesn’t prevent the same candidate itemset from being generated more than once. w E. g. , {Bread, Diapers, Milk} can be generated by merging w {Bread, Diapers} with {Milk}, w {Bread, Milk} with {Diapers}, or w {Diapers, Milk} with {Bread}. 20

Lexicographic Order u Avoid generating duplicate candidates by ensuring that the items in each frequent itemset are kept sorted in their lexicographic order. u Each frequent (k 1) itemset X is then extended with frequent items that are lexicographically larger than the items in X. u For example, the itemset {Bread, Diapers} can be augmented with {Milk} since Milk is lexicographically larger than Bread and Diapers. u However, we don’t augment {Diapers, Milk} with {Bread} nor {Bread, Milk} with {Diapers} because they violate the lexicographic ordering condition. u Why is it complete? 21

Prunning u. E. g. merging {Beer, Diapers} with {Milk} is unnecessary because one of its subsets, {Beer, Milk}, is infrequent. u. Solution: Prune! u. How? 22

Fk 1 F 1 Example {Beer, Diapers, Bread} and {Bread, Milk, Beer} aren't in fact generated if lexicographical ord. is considered. 23

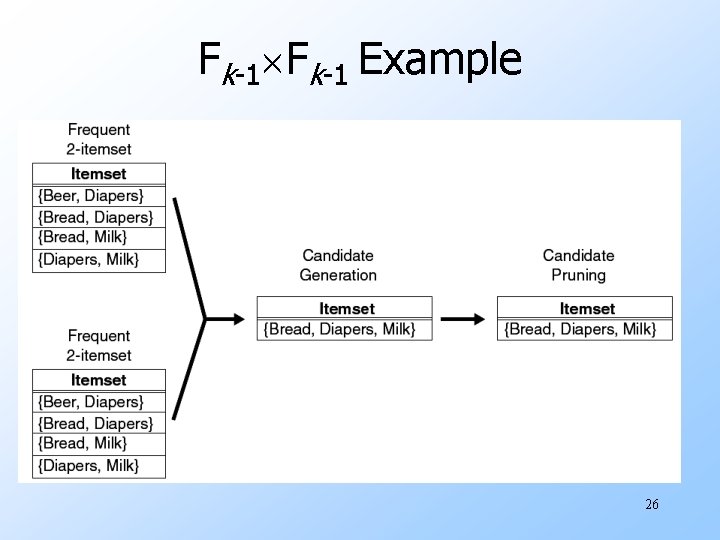
Fk 1 Method u Merge a pair of frequent (k 1) itemsets only if their first k 2 items are identical. u E. g. frequent itemsets {Bread, Diapers} and {Bread, Milk} are merged to form a candidate 3 itemset {Bread, Diapers, Milk}. 24

Fk 1 Method u We don’t merge {Beer, Diapers} with {Diapers, Milk} because the first item in both itemsets is different. But, is this "don't merge" decision Ok? u Indeed, if {Beer, Diapers, Milk} is a viable candidate, it would have been obtained by merging {Beer, Diapers} with {Beer, Milk} instead. Pruning u However, because each candidate is obtained by merging a pair of frequent (k 1) itemsets, an additional candidate pruning step is needed to ensure that the remaining k 2 subsets of k 1 elements are frequent. 25

Fk 1 Example 26

Another Example Min_sup_count = 2 C 1 TID List of item ID’s Itemset T 1 I 1, I 2, I 5 {I 1} T 2 I 2, I 4 T 3 F 1 Itemset Sup. count {I 2} {I 1} 6 I 2, I 3 {I 3} {I 2} 7 T 4 I 1, I 2, I 4 {I 4} {I 3} 6 T 5 I 1, I 3 {I 5} {I 4} 2 T 6 I 2, I 3 {I 5} 2 T 7 I 1, I 3 T 8 I 1, I 2, I 3, I 5 T 9 I 1, I 2, I 3 27

Generate C 2 from F 1 Min_sup_count = 2 TID List of item ID’s T 1 I 1, I 2, I 5 T 2 I 2, I 4 T 3 I 2, I 3 T 4 I 1, I 2, I 4 T 5 I 1, I 3 T 6 I 2, I 3 T 7 F 1 Itemset C 2 Sup. count Itemset Sup. C {I 1, I 2} 4 {I 1} 6 {I 1, I 3} 4 {I 2} 7 {I 1, I 4} 1 {I 3} 6 {I 1, I 5} 2 {I 4} 2 {I 2, I 3} 4 {I 5} 2 {I 2, I 4} 2 I 1, I 3 {I 2, I 5} 2 T 8 I 1, I 2, I 3, I 5 {I 3, I 4} 0 T 9 I 1, I 2, I 3 {I 3, I 5} 1 {I 4, I 5} 0 28

Generate C 3 from F 2 Min_sup_count = 2 F 2 Prune TID List of item ID’s Itemset Sup. C Itemset T 1 I 1, I 2, I 5 {I 1, I 2} 4 {I 1, I 2, I 3} T 2 I 2, I 4 {I 1, I 3} 4 {I 1, I 2, I 5} T 3 I 2, I 3 {I 1, I 5} 2 {I 1, I 3, I 5} T 4 I 1, I 2, I 4 {I 2, I 3} 4 {I 2, I 3, I 4} T 5 I 1, I 3 {I 2, I 4} 2 {I 2, I 3, I 5} T 6 I 2, I 3 {I 2, I 5} 2 {I 2, I 4, I 5} T 7 I 1, I 3 T 8 I 1, I 2, I 3, I 5 T 9 I 1, I 2, I 3 F 3 Itemset Sup. C {I 1, I 2, I 3} 2 {I 1, I 2, I 5} 2 29

Generate C 4 from F 3 Min_sup_count = 2 C 4 TID List of item ID’s Itemset T 1 I 1, I 2, I 5 {I 1, I 2, I 3, I 5} T 2 I 2, I 4 T 3 I 2, I 3 T 4 I 1, I 2, I 4 T 5 I 1, I 3 T 6 I 2, I 3 T 7 I 1, I 3 T 8 I 1, I 2, I 3, I 5 T 9 I 1, I 2, I 3 {I 1, I 2, I 3, I 5} is pruned because {I 2, I 3, I 5} is infrequent F 3 Itemset Sup. C {I 1, I 2, I 3} 2 {I 1, I 2, I 5} 2 30