Assignment Problem Dynamic Programming The Assignment Problem G

Assignment Problem, Dynamic Programming

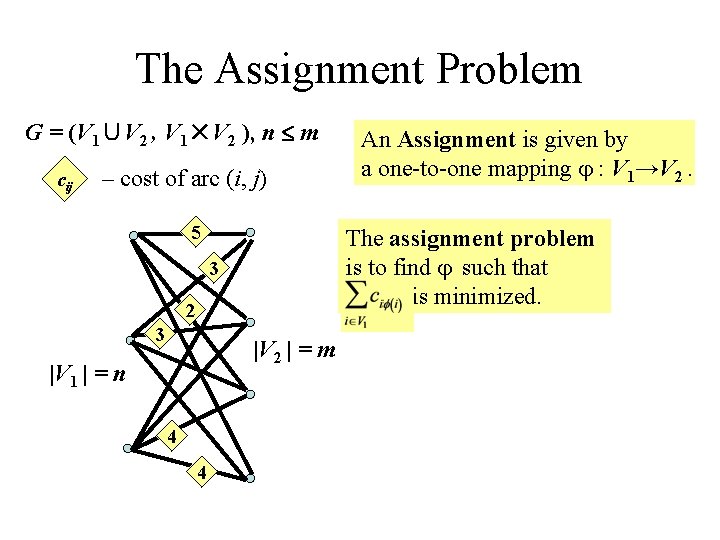
The Assignment Problem G = (V 1∪V 2 , V 1×V 2 ), n m cij – cost of arc (i, j) 5 The assignment problem is to find such that is minimized. 3 2 3 |V 2 | = m |V 1 | = n 4 4 An Assignment is given by a one-to-one mapping : V 1→V 2.

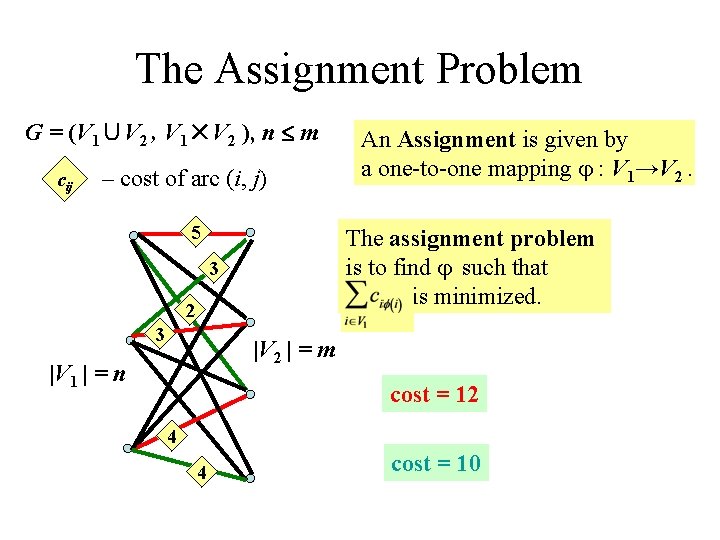
The Assignment Problem G = (V 1∪V 2 , V 1×V 2 ), n m cij – cost of arc (i, j) 5 The assignment problem is to find such that is minimized. 3 2 3 An Assignment is given by a one-to-one mapping : V 1→V 2. |V 2 | = m |V 1 | = n cost = 12 4 4 cost = 10

LP formulation of the Assignment Problem

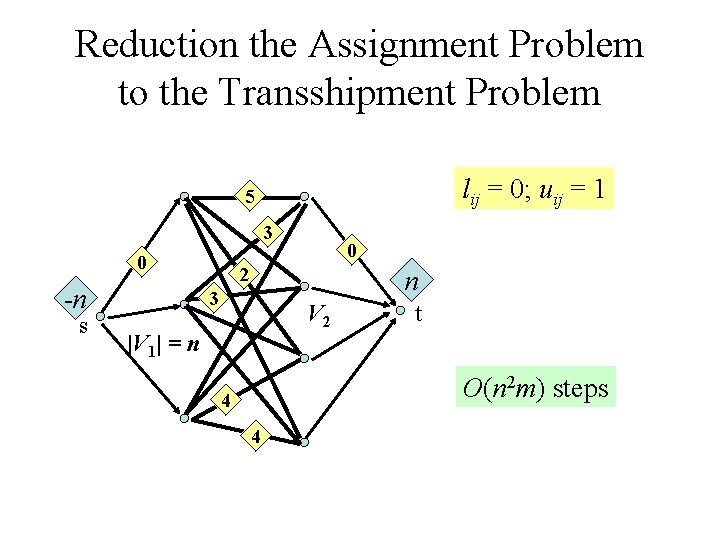
Reduction the Assignment Problem to the Transshipment Problem lij = 0; uij = 1 5 3 0 -n s 0 2 n 3 V 2 |V 1| = n t O(n 2 m) steps 4 4

1|ri; pi = 1|Σfi • Given are n jobs J 1 , . . . , Jn with unit processing times to be processed on a single machine, release dates ri and monotone (nondecreasing) functions fi of the finish times Ci of jobs i = 1, . . . , n. • Task: Find a schedule that minimizes the total sum of cost functions.

Jobs and Time Slots • • • Because the functions fi are monotone nondecreasing, the jobs should be scheduled as early as possible. The n earliest time slots ti for scheduling n jobs may be calculated using the following algorithm, in which we assume that the jobs are enumerated in such a way that r 1 r 2 . . . rn. Algorithm Time Slots t 1 : = r 1 FOR i : = 2 TO n DO ti : = max { ri , ti– 1 + 1 }

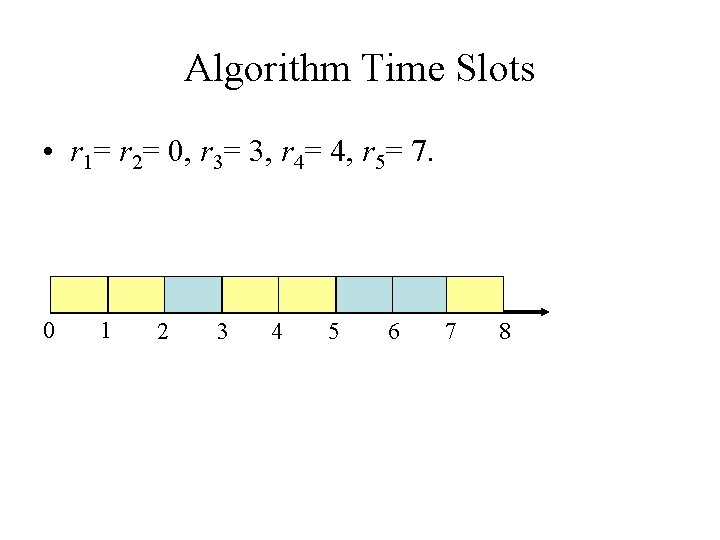
Algorithm Time Slots • r 1= r 2= 0, r 3= 3, r 4= 4, r 5= 7. 0 1 2 3 4 5 6 7 8

Time slots • Lemma 3. 1 There exists an optimal schedule which occupies all of the time slots ti, i = 1, …, n.

Proof • Consider an optimal schedule σ which occupies time slots t 1, …, tj where j < n is maximal. • According to the construction of the ti-values, tj+1 is the next time slot in which a job can be scheduled. • If time slot tj+1 in σ is empty, a job scheduled later in σ can be moved to tj+1 without increasing the objective value. • Thus, the new schedule is optimal, too, and we have a contradiction to the maximality of j.

1|ri; pi = 1|Σfi to Assignment Problem

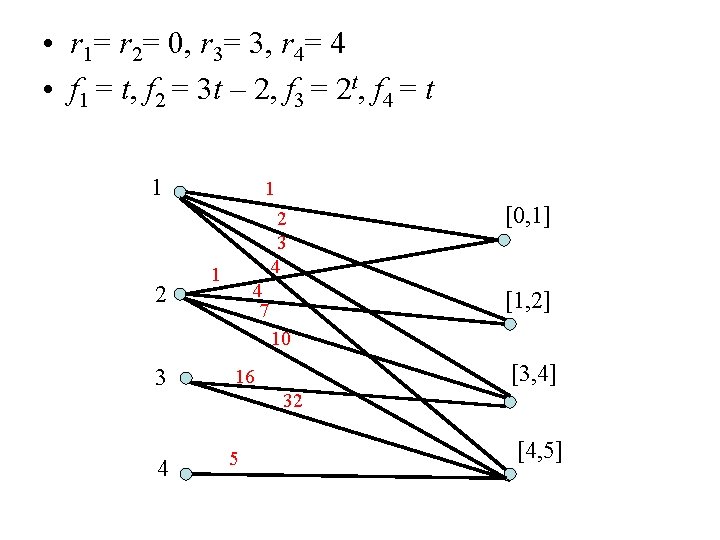
• r 1= r 2= 0, r 3= 3, r 4= 4 • f 1 = t, f 2 = 3 t – 2, f 3 = 2 t, f 4 = t 1 2 3 4 1 4 7 [0, 1] [1, 2] 10 3 16 4 5 [3, 4] 32 [4, 5]

Special Assignment Problem • Let V 1 = {v 1, . . . , vn} and V 2 = {v 1, . . . , vm} and consider the correspondent complete bipartite graph G = (V 1∪V 2 , V 1×V 2 ). Then the correspondent assignment problem is completely specified by a n×m array C = (cij). • C is called a Monge array if cik + cjl cil + cjk for all i < j and k < l. (2. 11)

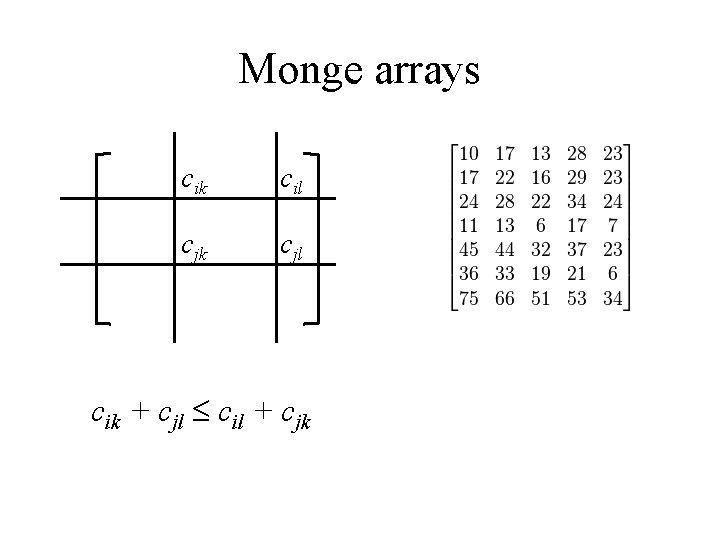
Monge arrays cik cil cjk cjl cik + cjl cil + cjk

Monge Array Theorem 3. 2

Proof • Let y = (yij) be an optimal solution of the assignment problem with yuu = 1 for u = 1, … , i where i is as large as possible. • Assume that i < n (if i = n we have finished). • Because yi+1, i+1 = 0, there exists an index l > i+1 with yi+1, l = 1. • Now we consider two cases.

Proof (Case 1)

Proof (Case 2)

Monge Array (2) • Corollary 3. 3

Monge Array (3) • Corollary 3. 4

P||ΣCj • Given are n jobs J 1 , . . . , Jn to be processed on m identical parallel machines M 0, . . . , Mm-1. • Task: Find a schedule that minimizes the sum of completion times of jobs.

Structure of Schedule • A schedule σ is given by a partition of the set of jobs into m disjoints sets I 0 , . . . , Im-1 and for each Ij, a sequence of the jobs in Ij. Assume that Ij contains nj elements and that j(i) (i = 1, . . . , n) is the job to be scheduled in position nj – i + 1 on machine Mj. We assume that the jobs in Ij are scheduled on Mj starting at time zero without idle times. Then the value of the objective function is

Assignment Problem • Now consider the assignment problem with cik = aibk where ai = pi for i = 1, . . . , n and bk = k / m for k = 1, . . . , n. A schedule σ corresponds with an assignment with the objective value • In this schedule job i is assigned to the bk -last position on a machine if i is assigned to k.

Optimal Schedule • Now if we assume that p 1 ≥ p 2 ≥. . . ≥ pn then we get an optimal assignment if we assign ai = pi to bi (i = 1, . . . , n). • This assignment corresponds with a schedule in which job i is scheduled on machine (i – 1)mod(m). Furthermore, on each machine the jobs are scheduled according to nondecreasing processing times.

1||Σwj Uj • Given n jobs J 1 , . . . , Jn with processing times pi and due dates di. • Task: Find a sequence these jobs such that the weighted number of late jobs is minimized where wj ≥ 0 for i = 1, . . . , n.

Structure of Optimal Schedule Assume that the jobs are enumerated according to nondecreasing due dates: d 1 d 2 . . . dn. Then the exist an optimal schedule given by a sequence of the form i 1, i 2 , . . . , is+1, . . . , in where jobs with indices i 1< i 2 <. . . < is are ontime and jobs with indices is+1, . . . , in are late. J 1 0 J 3 J 4 J 7 J 8 J 2 J 5 J 6

Dynamic Programming • To solve the problem, we calculate recursively for t = 0, 1, . . . , T and j = 1, . . . , n the minimum criterion value Fj(t) for the first j jobs, subject to the constraint that the total processing time of the on-time jobs is at most t. If 0 t dj and job Jj is on-time in a schedule which corresponds with Fj(t) then Fj(t) = Fj– 1(t – pj). Otherwise Fj(t) = Fj– 1(t) + wj. If t > dj then Fj(t) = Fj(dj) because all jobs J 1 , J 2 , . . . , Jj finishing later than dj ≥. . . ≥ d 1 are late.

Recursion

Algorithm 1||Σwj Uj 1. for t : = –pmax to – 1 do 2. for j : = 0 to n do Fj(t) = ∞; 3. for t : = 0 to T do F 0(t) = 0; 4. for j : = 1 to n do begin 5. for t : = 0 to dj do 6. if Fj– 1(t) + wj < Fj– 1(t – pj) then Fj(t) = Fj– 1(t) + wj else Fj(t) = Fj– 1(t – pj); 7. for t : = dj + 1 to T do Fj(t) = Fj(dj) end

Algorithm Backward Calculation • t : = dn ; L : = • for j : = n down to 1 do begin t : = min{t, di}; if Fj(t) = Fj– 1(t) + wj then L : = L∪{Jj} else t : = t – pi end

P||Σwj Cj • Given: n jobs J 1 , . . . , Jn are to be processed on m identical parallel machines. Each job Ji has processing time pi and weight wi. • Task: Find a sequence these jobs such that the sum of the weighted completion times is minimized. All wj ≥ 0 are assumed to be positive.

Optimal Solution of 1||Σwj Cj An optimal solution of this one machine problem is obtained if we sequence the jobs according nondecreasing ratios pi/wi.

Interchange Argument Let j be a job which is scheduled immediately before job i. If we interchange i and j, the objective function changed by wipi + wj(pi + pj) – wjpj – wi(pi + pj) = wjpi – wi pj which is nonpositive if and only if pi/wi pj/wj. Thus, the objective function does not increase if i and j are interchanged.

Structure of Optimal Schedule of P||Σwj Cj • A consequence of this result is that in an optimal solution of problem P||Σwj Cj , jobs to be processed on the same machine must be processed in order of nondecreasing ratios pi/wi. • Therefore we assume that all jobs are indexed such that p 1/w 1 p 2/w 2 . . . pn/wn.

Recursion

Exercises • Prove Corollary 3. 2 and Corollary 3. 3. • Suppose f is strictly increasing, positive function. That is, f(x) > 0 for all x > 0 and f(x) > f(y) whenever x > y. Show that SPT (short processing time first) gives an optimal schedule for the problem 1||ΣCj 2.

Exercise 2. 1 • Find an optimal schedule for the following instance of O|pmtn|Cmax problem. M 1 M 2 M 3 J 1 3 5 7 J 2 4 2 2 J 3 6 3 1 J 4 2 4 3

Exercise 2. 2 • Find an optimal schedule for the following instance of 1|ri; pi = 1|Σfi problem. J 1 J 2 J 3 J 4 J 5 J 6 rj 0 0 0 1 5 5 fj x x+3 2 x x 2–x 20 x x 2

Exercise 2. 3 • Find an optimal schedule for the following instance of P 3||ΣCi problem. J 1 J 2 J 3 J 4 J 5 J 6 J 7 J 8 J 9 J 10 pj 1 1 3 7 5 2 5 4 9 6