ASSIGNMENT Newtons method Lagrange polynomial Polynomial Interpolation Cubic


ASSIGNMENT Newton’s method 또는 Lagrange polynomial 을 사용 한 Polynomial Interpolation과 Cubic Spline을 비교하 라. Example) 다음 데이터들을 통해 ln 2의 값을 예측하라. ln (1) = 0 ln (4) = 1. 386294 ln (6) = 1. 791759 ln (1. 5이하 2. 5이상의 임의의 값) = f(값)

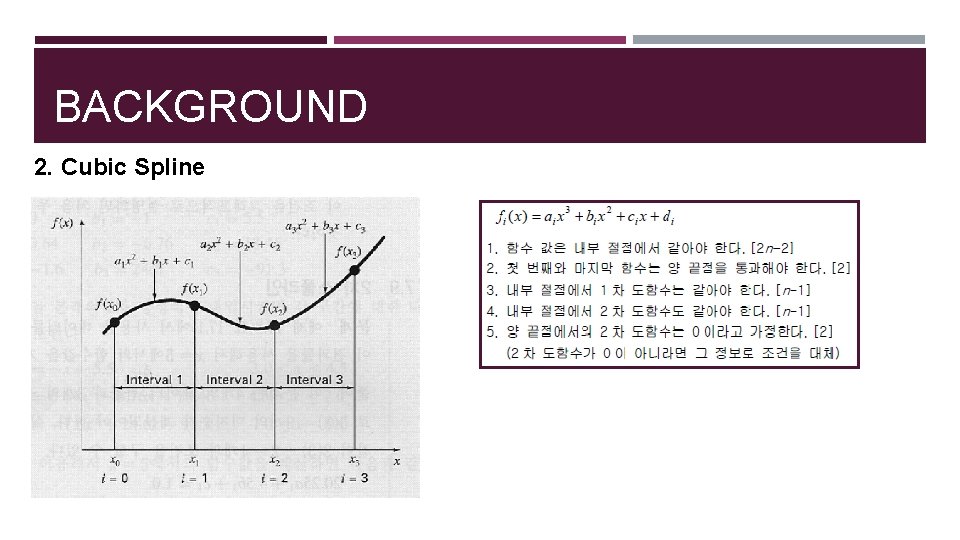
BACKGROUND 2. Cubic Spline
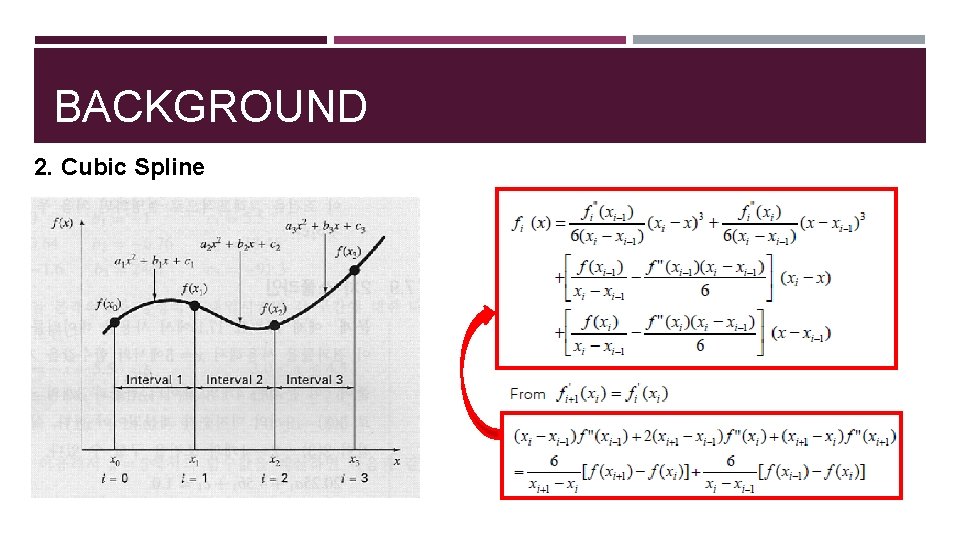
BACKGROUND 2. Cubic Spline
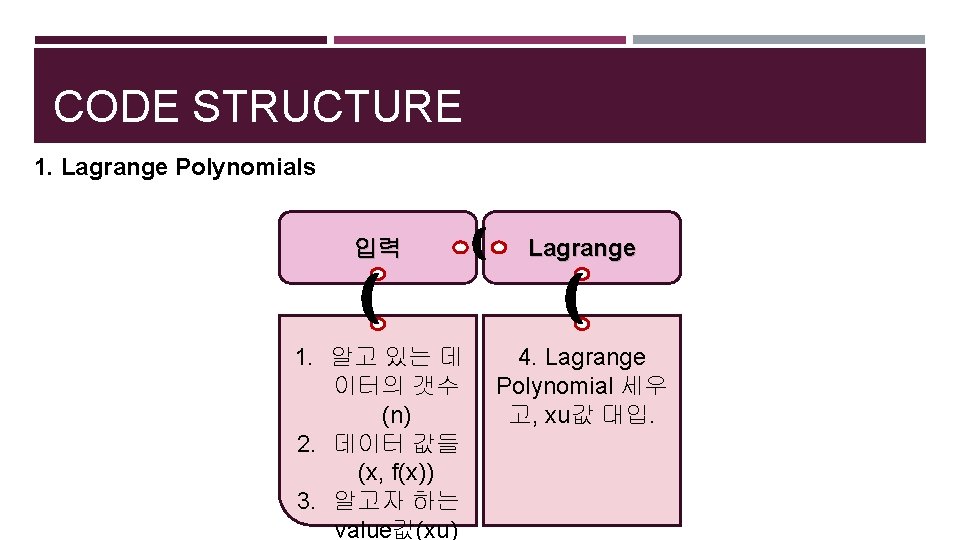
CODE STRUCTURE 1. Lagrange Polynomials 입력 Lagrange 1. 알고 있는 데 이터의 갯수 (n) 2. 데이터 값들 (x, f(x)) 3. 알고자 하는 value값(xu) 4. Lagrange Polynomial 세우 고, xu값 대입.

CODE STRUCTURE 2. Cubic Spline

CODE STRUCTURE 2. Cubic Spline (1) (2) (1) : Matrix e(1 : n- (3) 2) Matrix A(n-2 by n-2) 생성 (2) : Matrix f(1 : n(4) 2) (3) : Matrix g(1 : n 2) (4) : Matrix r(1 : n 2)

KEY CODE 1. Lagrange Polynomials

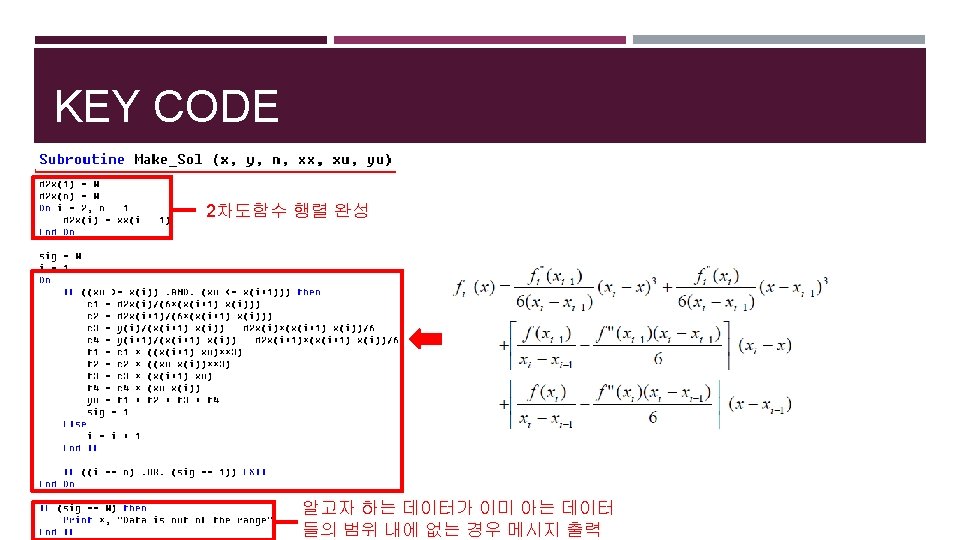
KEY CODE 2. Cubic Spline

KEY CODE

KEY CODE
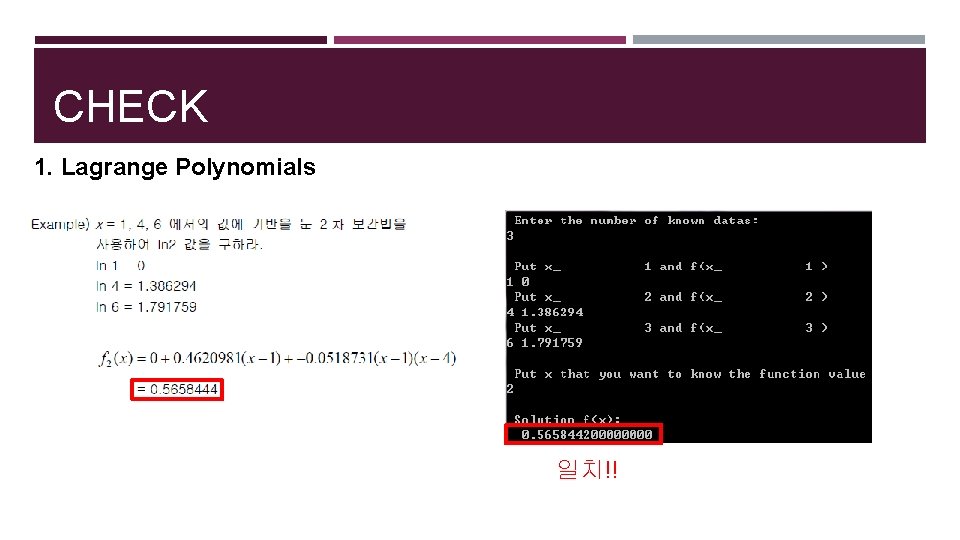
CHECK 1. Lagrange Polynomials 일치!!
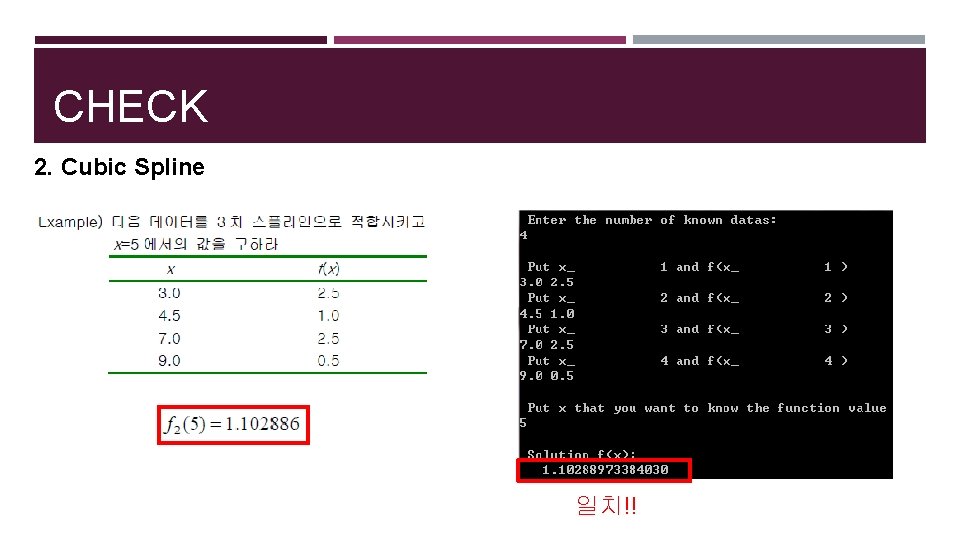
CHECK 2. Cubic Spline 일치!!

RESULT & ANALYSIS Example) 다음 데이터들을 통해 ln 2의 값을 예측하라. ln (1) = 0 ln (4) = 1. 386294 ln (6) = 1. 791759 ln (1. 5이하 2. 5이상의 임의의 X 4) = f(X 4) 참값 ln 2 = 0. 6931471805599453


RESULT & ANALYSIS 1. 3개의 known data 들만 가지고 값을 구한 경우 (1) Lagrange Polynomials (2) Cubic Spline V S 오차율 = 18. 366% 오차율 = 23. 355%
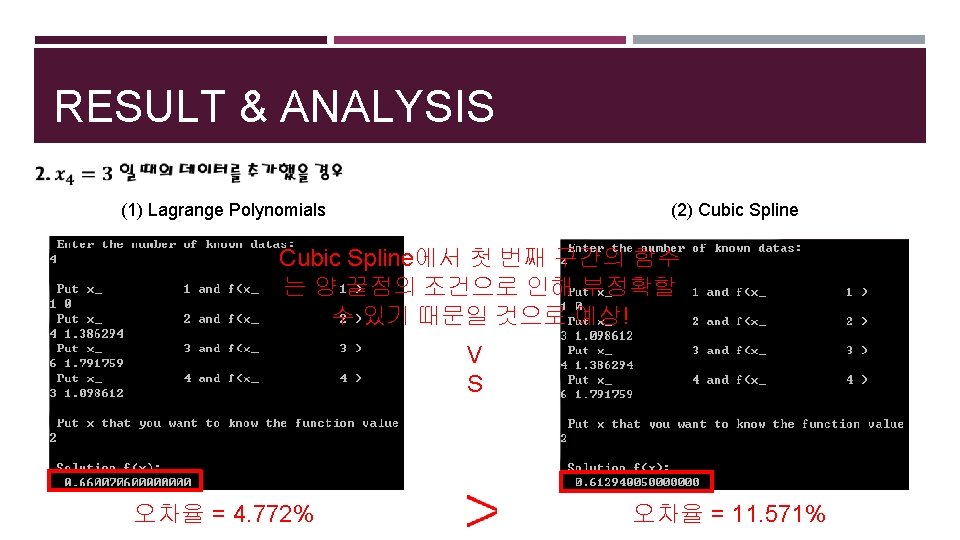
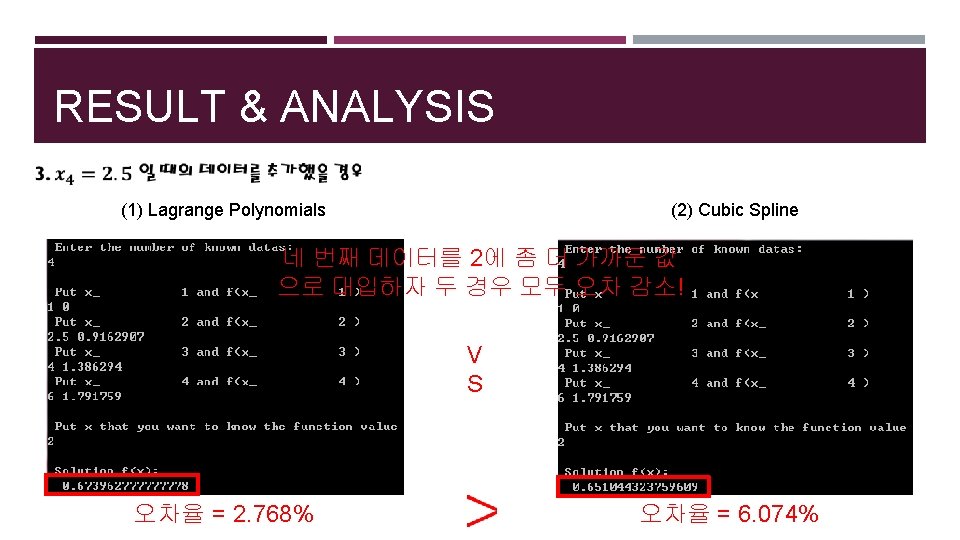
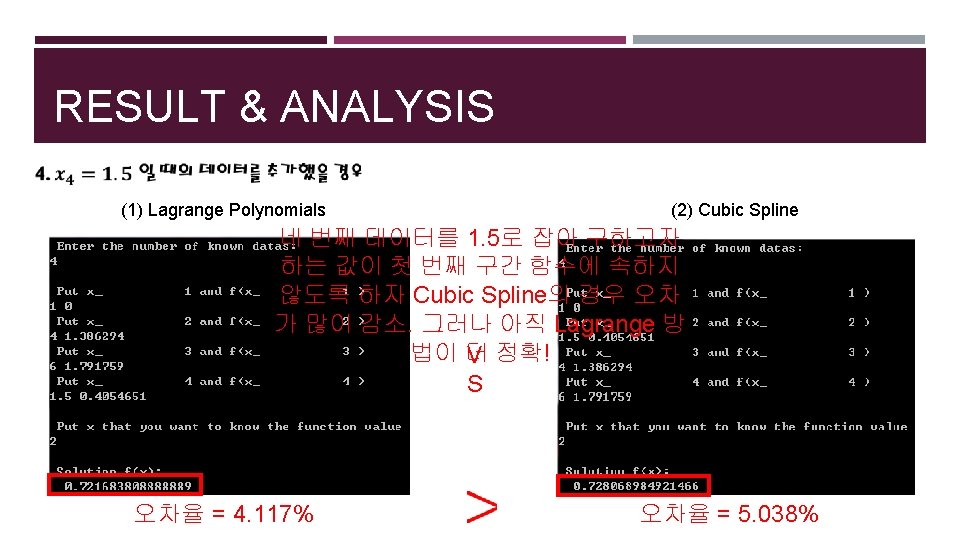

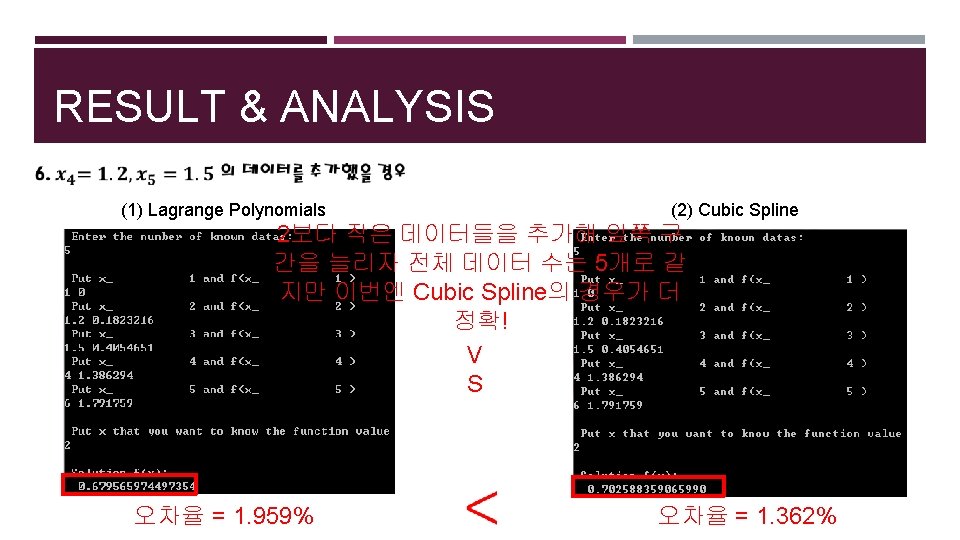
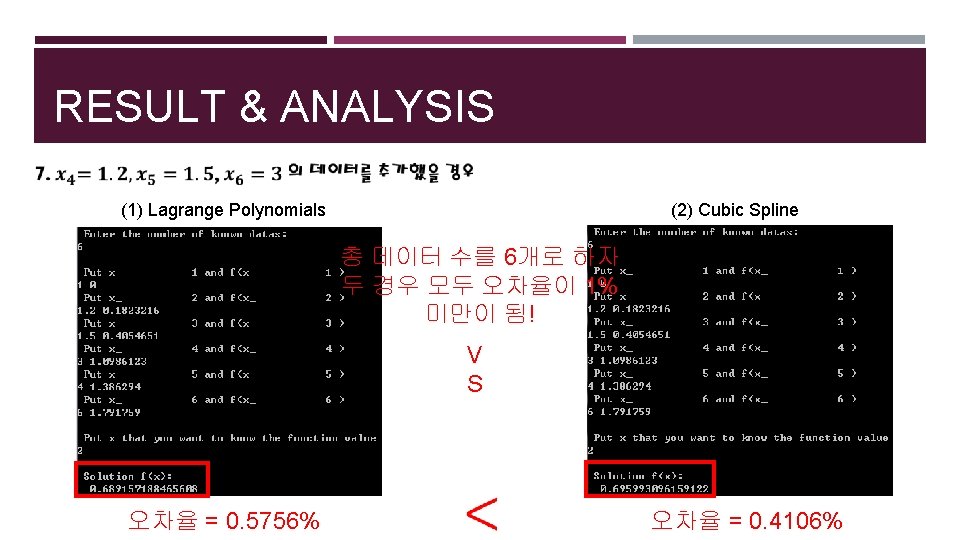
RESULT & ANALYSIS (1) Lagrange Polynomials (2) Cubic Spline 총 데이터 수를 6개로 하자 두 경우 모두 오차율이 1% 미만이 됨! V S 오차율 = 0. 5756% 오차율 = 0. 4106%


THANK YOU
- Slides: 28