Assessing and Comparing Classification Algorithms Introduction Resampling and


















- Slides: 27

Assessing and Comparing Classification Algorithms • Introduction • Resampling and Cross Validation • Measuring Error • Interval Estimation and Hypothesis Testing • Assessing and Comparing Performance

Introduction n Questions: ¨ Assessment of the expected error of a learning algorithm: Is the error rate of 1 -NN less than 2%? ¨ Comparing the expected errors of two algorithms: Is k. NN more accurate than MLP ? Training/validation/test sets Resampling methods: K-fold cross-validation 2 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

Algorithm Preference n n Criteria (Application-dependent): ¨ Misclassification error, or risk (loss functions) ¨ Training time/space complexity ¨ Testing time/space complexity ¨ Interpretability ¨ Easy programmability Cost-sensitive learning 3 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

Assessing and Comparing Classification Algorithms • Introduction • Resampling and Cross Validation • Measuring Error • Interval Estimation and Hypothesis Testing • Assessing and Comparing Performance

Resampling and K-Fold Cross-Validation n The need for multiple training/validation sets {Xi, Vi}i: Training/validation sets of fold i K-fold cross-validation: Divide X into k, Xi, i=1, . . . , K n Ti share K-2 parts n 5 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

5× 2 Cross-Validation n 5 times 2 fold cross-validation (Dietterich, 1998) 6 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

Bootstrapping n n Draw instances from a dataset with replacement Prob that we do not pick an instance after N draws that is, only 36. 8% is new! 7 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

Assessing and Comparing Classification Algorithms • Introduction • Resampling and Cross Validation • Measuring Error • Interval Estimation and Hypothesis Testing • Assessing and Comparing Performance

Measuring Error n n n Error rate Recall = # of errors / # of instances = (FN+FP) / N = # of found positives / # of positives = TP / (TP+FN) = sensitivity = hit rate Precision = # of found positives / # of found = TP / (TP+FP) Specificity = TN / (TN+FP) False alarm rate = FP / (FP+TN) = 1 - Specificity 9 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

Methods for Performance Evaluation n How to obtain a reliable estimate of performance? n Performance of a model may depend on other factors besides the learning algorithm: Class distribution ¨ Cost of misclassification ¨ Size of training and test sets ¨

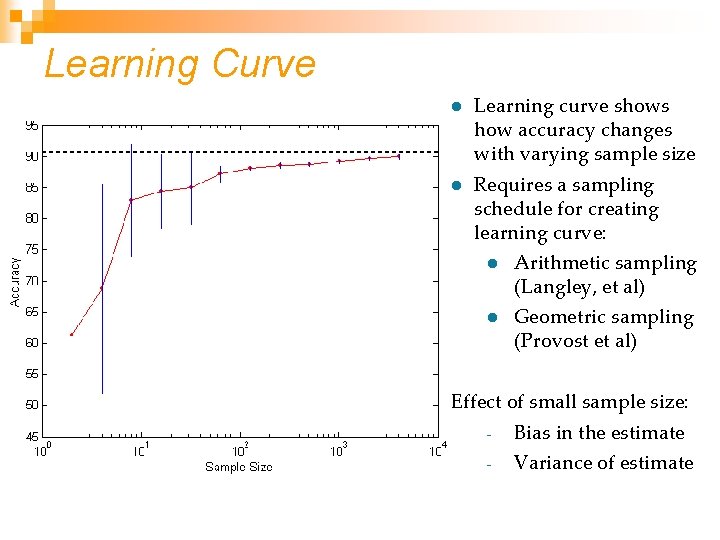
Learning Curve l Learning curve shows how accuracy changes with varying sample size l Requires a sampling schedule for creating learning curve: l Arithmetic sampling (Langley, et al) l Geometric sampling (Provost et al) Effect of small sample size: - Bias in the estimate - Variance of estimate

ROC (Receiver Operating Characteristic) http: //en. wikipedia. org/wiki/Receiver_operating_characteristic n Developed in 1950 s for signal detection theory to analyze noisy signals ¨ n n Characterize the trade-off between positive hits and false alarms ROC curve plots TP (on the y-axis) against FP (on the xaxis) Performance of each classifier represented as a point on the ROC curve ¨ changing the threshold of algorithm, sample distribution or cost matrix changes the location of the point http: //www. childrensmercy. org/stats/ask/roc. asp

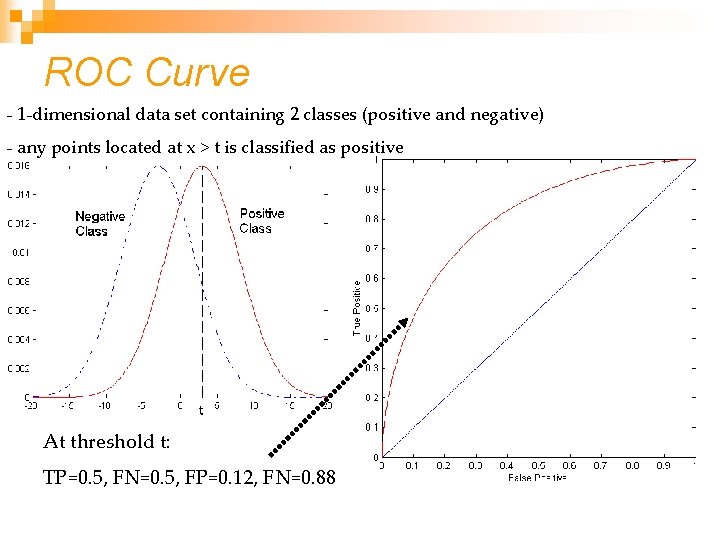
ROC Curve - 1 -dimensional data set containing 2 classes (positive and negative) - any points located at x > t is classified as positive At threshold t: TP=0. 5, FN=0. 5, FP=0. 12, FN=0. 88

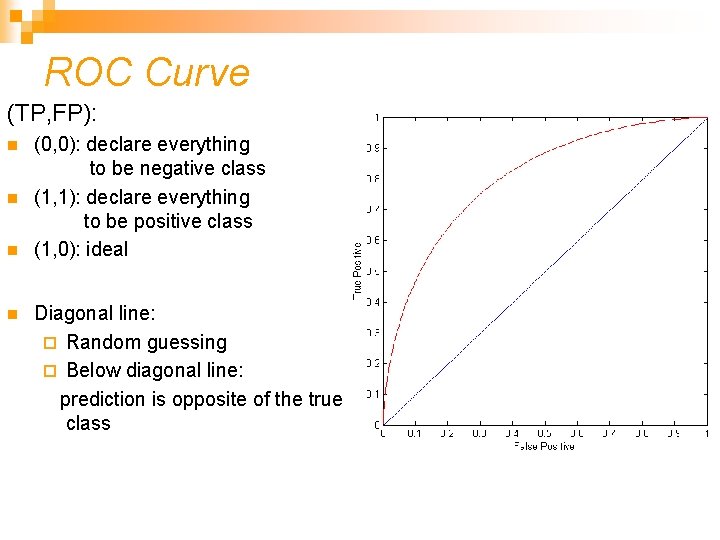
ROC Curve (TP, FP): n n (0, 0): declare everything to be negative class (1, 1): declare everything to be positive class (1, 0): ideal Diagonal line: ¨ Random guessing ¨ Below diagonal line: prediction is opposite of the true class

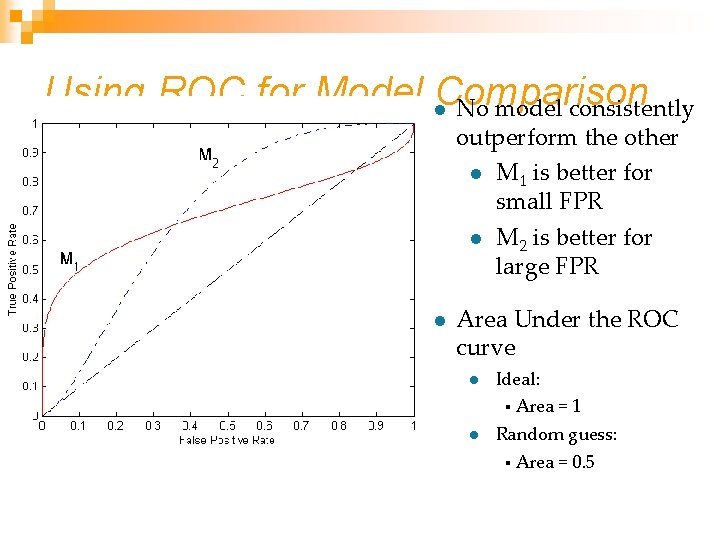
Using ROC for Model l. Comparison No model consistently outperform the other l M 1 is better for small FPR l M 2 is better for large FPR l Area Under the ROC curve l Ideal: § l Area = 1 Random guess: § Area = 0. 5

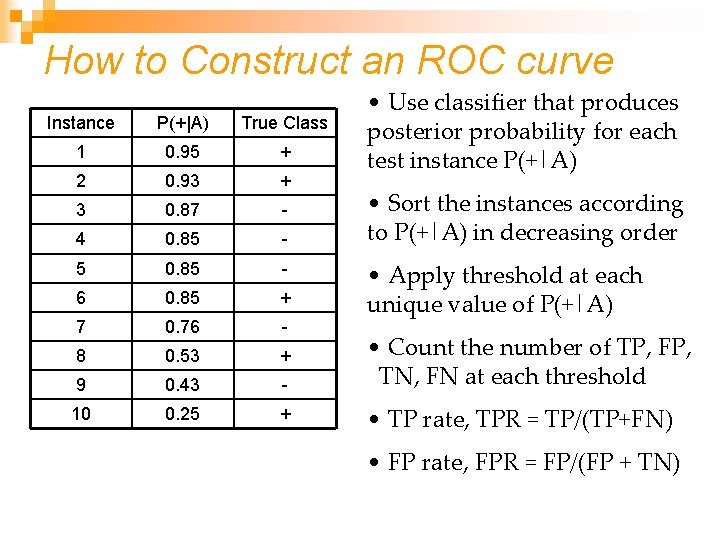
How to Construct an ROC curve Instance P(+|A) True Class 1 0. 95 + 2 0. 93 + 3 0. 87 - 4 0. 85 - 5 0. 85 - 6 0. 85 + 7 0. 76 - 8 0. 53 + 9 0. 43 - 10 0. 25 + • Use classifier that produces posterior probability for each test instance P(+|A) • Sort the instances according to P(+|A) in decreasing order • Apply threshold at each unique value of P(+|A) • Count the number of TP, FP, TN, FN at each threshold • TP rate, TPR = TP/(TP+FN) • FP rate, FPR = FP/(FP + TN)

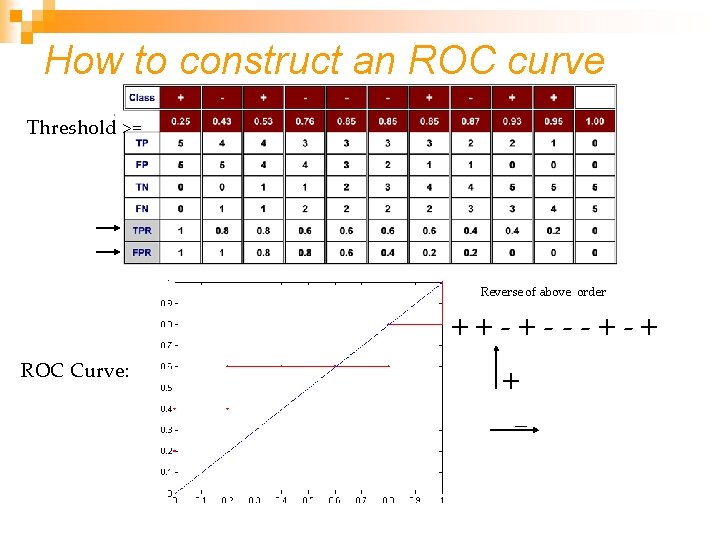
How to construct an ROC curve Threshold >= Reverse of above order ++-+---+-+ ROC Curve: + -

Assessing and Comparing Classification Algorithms • Introduction • Resampling and Cross Validation • Measuring Error • Interval Estimation and Hypothesis Testing • Assessing and Comparing Performance

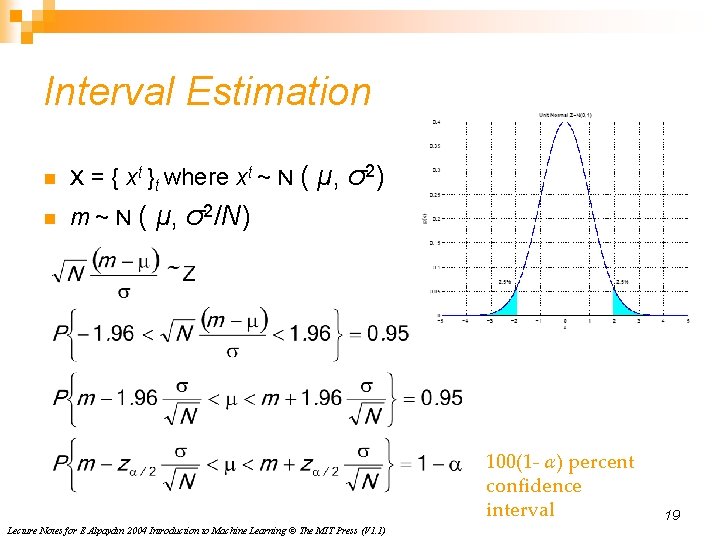
Interval Estimation n X = { xt }t where xt ~ N ( μ, σ2) n m ~ N ( μ, σ2/N) 100(1 - α) percent confidence interval Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1) 19

When σ2 is not known: 20 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

Hypothesis Testing n n Reject a null hypothesis if not supported by the sample with enough confidence X = { xt }t where xt ~ N ( μ, σ2) H 0: μ = μ 0 vs. H 1: μ ≠ μ 0 Accept H 0 with level of significance α if μ 0 is in the 100(1α) confidence interval Two-sided test 21 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

n One-sided test: H 0: μ ≤ μ 0 vs. H 1: μ > μ 0 Accept if n Variance unknown: Use t, instead of z Accept H 0: μ = μ 0 if 22 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

Assessing and Comparing Classification Algorithms • Introduction • Resampling and Cross Validation • Measuring Error • Interval Estimation and Hypothesis Testing • Assessing and Comparing Performance

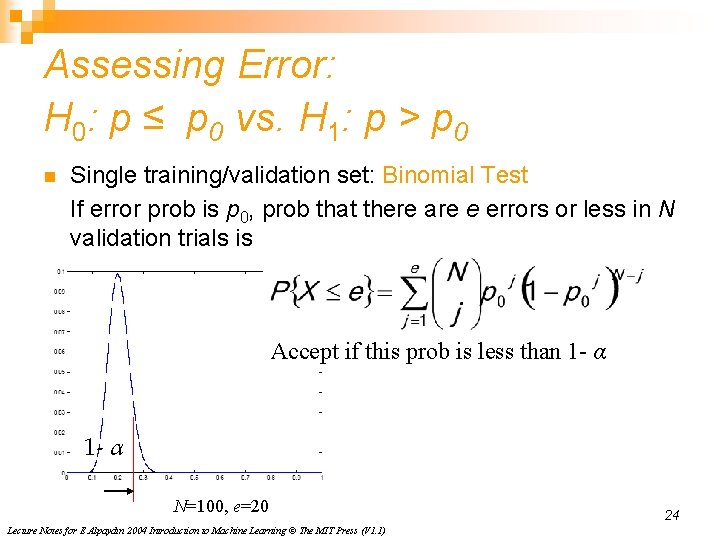
Assessing Error: H 0: p ≤ p 0 vs. H 1: p > p 0 n Single training/validation set: Binomial Test If error prob is p 0, prob that there are e errors or less in N validation trials is Accept if this prob is less than 1 - α N=100, e=20 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1) 24

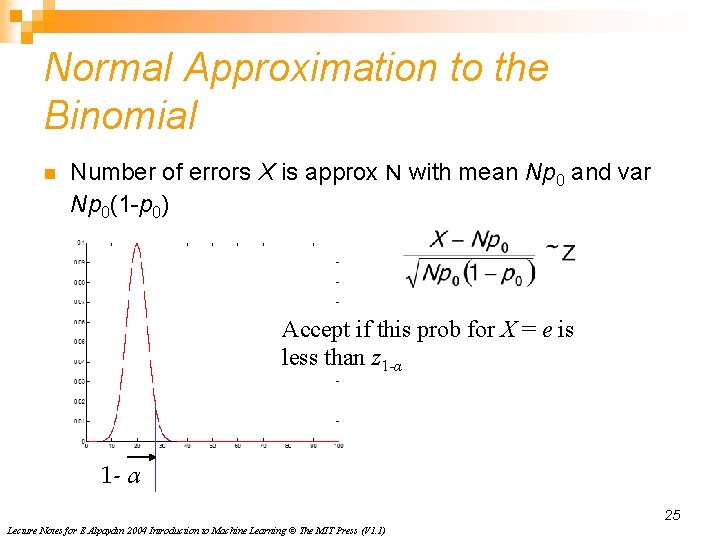
Normal Approximation to the Binomial n Number of errors X is approx N with mean Np 0 and var Np 0(1 -p 0) Accept if this prob for X = e is less than z 1 -α 1 - α 25 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

Paired t Test n n Multiple training/validation sets xti = 1 if instance t misclassified on fold i Error rate of fold i: With m and s 2 average and var of pi we accept p 0 or less error if is less than tα, K-1 26 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)

K-Fold CV Paired t Test n n Use K-fold cv to get K training/validation folds pi 1, pi 2: Errors of classifiers 1 and 2 on fold i pi = pi 1 – pi 2 : Paired difference on fold i The null hypothesis is whether pi has mean 0 27 Lecture Notes for E Alpaydın 2004 Introduction to Machine Learning © The MIT Press (V 1. 1)