Asservissement et rgulation continu Chapitre 3 Etude frquentielle

Asservissement et régulation continu

Chapitre 3 Etude fréquentielle de systèmes Sujets abordés du chapitre 3. 1) Fonction de transfert fréquentielle 3. 1. 1) Réponse harmonique d’un système 3. 1. 2) Représentation graphique de FTF 3. 2) Diagrammes de Bode des systèmes du 1 er ordre 3. 2. 1) Tracés des diagrammes de Bode 3. 2. 2) Exploitation de diagrammes de Bode 3. 3) Diagrammes de Bode des systèmes du 2 ond ordre 3. 3. 1) Fonction de transfert fréquentielle 3. 3. 2) Tracés des diagrammes de Bode

Chapitre 3 Etude fréquentielle de systèmes 3. 1) Fonction de transfert fréquentielle 3. 1. 1) Réponse harmonique d’un système Considérons le système linéaire suivant : Question : Quelle est la sortie si l’entrée est un signal sinusoïdal ?

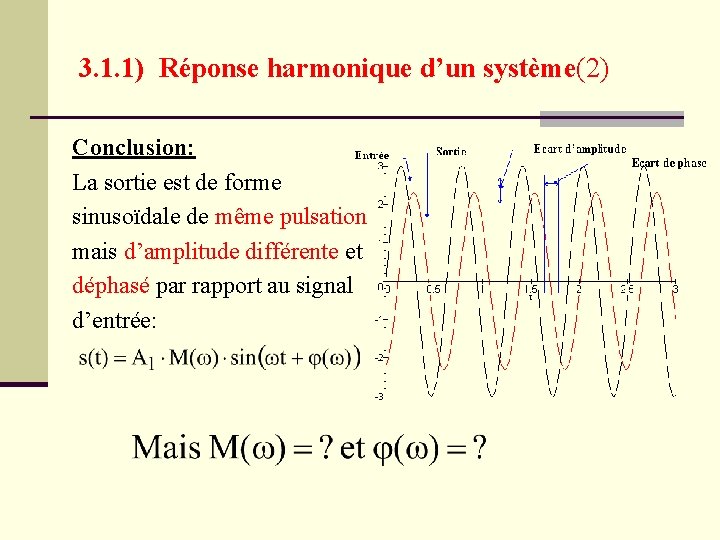
3. 1. 1) Réponse harmonique d’un système(2) Conclusion: La sortie est de forme sinusoïdale de même pulsation mais d’amplitude différente et déphasé par rapport au signal d’entrée:

3. 1. 1) Réponse harmonique d’un système(3)

3. 1. 2) Représentation graphique de H(jw) est une fonction complexe de la variable , l'étude de cette fonction peut se faire de manière graphique. On distingue principalement trois représentations graphiques de H(jw): Les diagrammes de BODE, n la représentation de NYQUIST, n la représentation de BLACK. n

3. 1. 2) Représentation graphique de H(jw) (2) n Diagrammes de Bode Définition Les diagrammes de Bode représentent séparément le module et la phase en fonction de dans le plan semi-logarithmique. n Le module est gradué en décibel noté n La phase est graduée en degré. :

3. 1. 2) Représentation graphique de H(jw) (3) n Lieu de Nyquist Le lieu de Nyquist est la représentation dans le plan complexe de la fonction: n La courbe doit être gradué dans le sens des n Utilité: Etude de la stabilité croissants:

3. 1. 2) Représentation graphique de H(jw) (4) n Lieu de Black On représente la phase comme coordonnée. en abscisse et le gain n Utilité: déterminer le correcteur PID

3. 2) Diagrammes de Bode du système du 1 er ordre 3. 2. 1) Tracé des diagrammes de Bode n Considérons le système suivant : H(p) = n Procédure de tracer les diagrammes de Bode

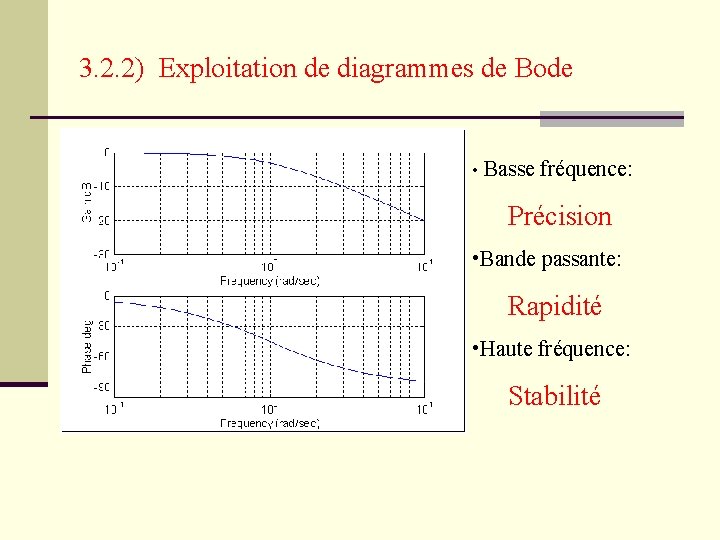
3. 2. 2) Exploitation de diagrammes de Bode • Basse fréquence: Précision • Bande passante: Rapidité • Haute fréquence: Stabilité

3. 3) Diagrammes de Bode du système du 2 ond ordre 3. 3. 1) Fonction de transfert fréquentielle n Considérons le système suivant : n Fonction de transfert fréquentielle

3. 3. 2) Tracé des diagrammes de Bode n Soit fonction de transfert fréquentielle n Procédure de tracer les diagrammes de Bode