ASPfun A Distributed Object Calculus and its Formalization

ASPfun: A Distributed Object Calculus and its Formalization in Isabelle Ludovic HENRIO Work realized in collaboration with Florian Kammüller and Henry Sudhof (Technische Universität Berlin) Montevideo, Nov 2007

Context -calculus: A Theory of Objects (Abadi, Cardelli) - Formalizes objects and typing - Several calculi: a functional and an imperative one ASP: Asynchronous Sequential Processes (Caromel, Henrio) - Based on imp-calculus - Distributed active object calculus - Asynchronous method calls (requests), futures Objective - Properties of confluence/determinism, e. g. execution Provide a framework for (mechanically) proving properties toobject-oriented the order of replies oninsensitive distributed languages and programs typing, confluence, …

Functional -calculus Syntax Each method is a function with a parameter: “self” Semantics (Abadi - Cardelli) Why functional? updating a field creates a new object (copy)

Contribution ASPfun calculus - Based on functional -calculus - Distributed with active objects and futures - Good representation of functional distributed programs (workflows, services) A type system for ASPfun: - Typing active objects and futures ASPfun is simpler - Proof of subject-reduction and progress no dead-lock Easier to formalize in Isabelle/HOL A Formalization in Isabelle/HOL A lot of interesting properties (no dead-lock) - Calculus and semantics - Type-system BUT further from a “real life” complete programming language - Proofs

Agenda 1 - ASPfun: syntax, semantics and properties 2 - A type system for ASPfun 3 - Formalization in Isabelle/HOL

ASPfun Syntax (static) One new construct: Active 1 - ASPfun: syntax, semantics and properties
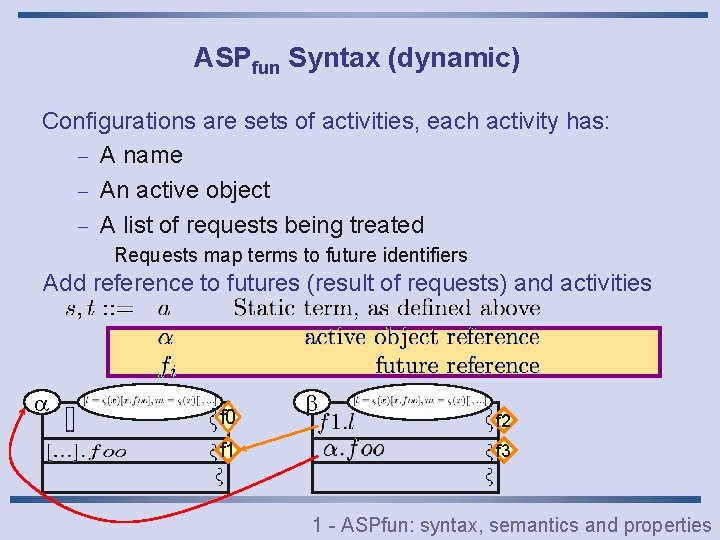
ASPfun Syntax (dynamic) Configurations are sets of activities, each activity has: - A name - An active object - A list of requests being treated Requests map terms to future identifiers Add reference to futures (result of requests) and activities f 0 f 1 f 2 f 3 1 - ASPfun: syntax, semantics and properties
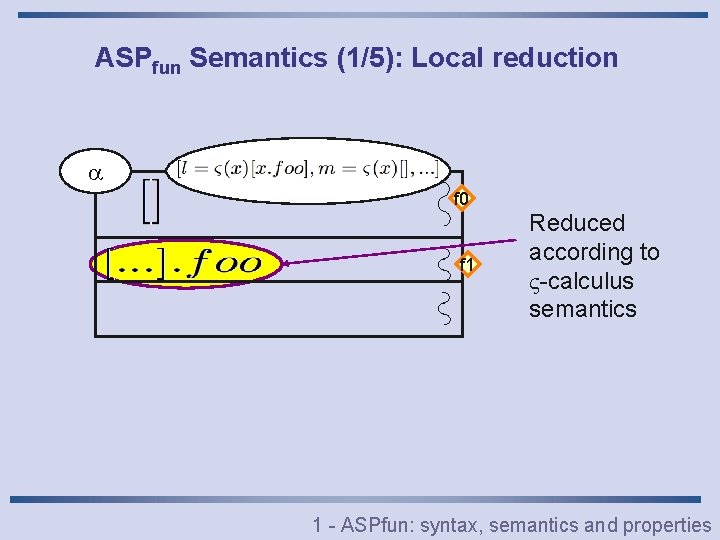
ASPfun Semantics (1/5): Local reduction f 0 f 1 Reduced according to -calculus semantics 1 - ASPfun: syntax, semantics and properties
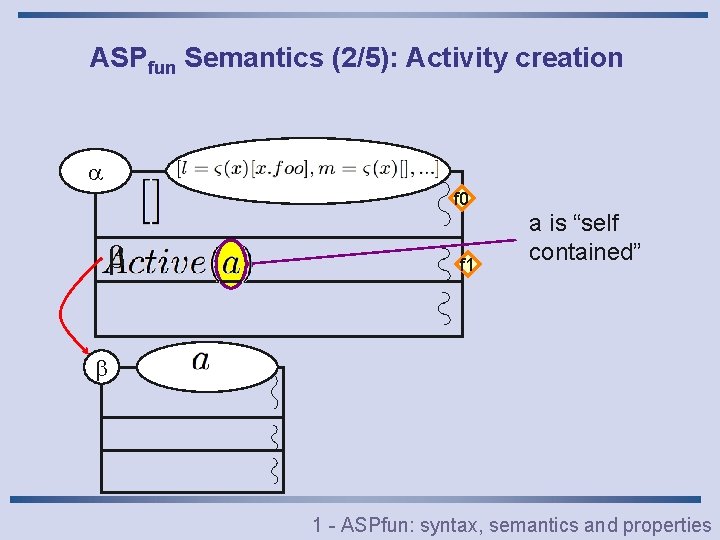
ASPfun Semantics (2/5): Activity creation f 0 f 1 a is “self contained” 1 - ASPfun: syntax, semantics and properties
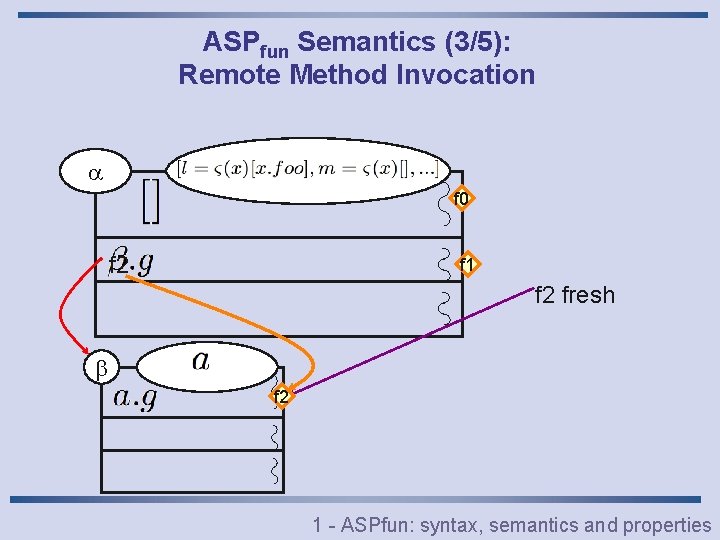
ASPfun Semantics (3/5): Remote Method Invocation f 0 f 2 f 1 f 2 fresh f 2 1 - ASPfun: syntax, semantics and properties
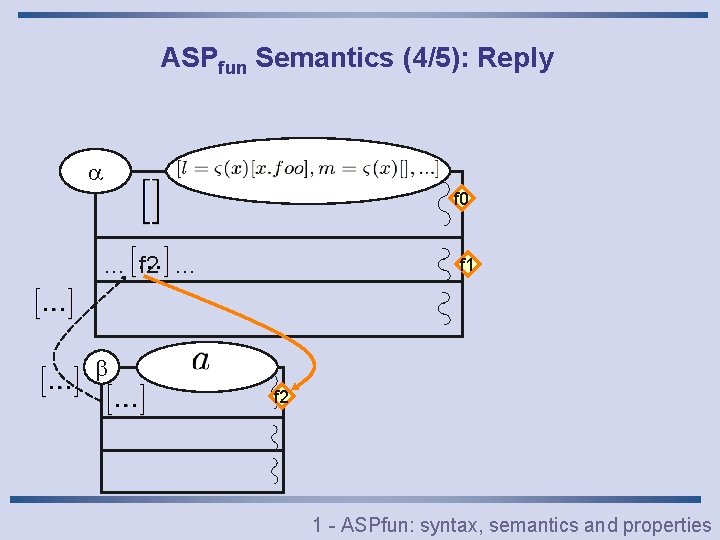
ASPfun Semantics (4/5): Reply f 0 … f 2 … f 1 f 2 1 - ASPfun: syntax, semantics and properties
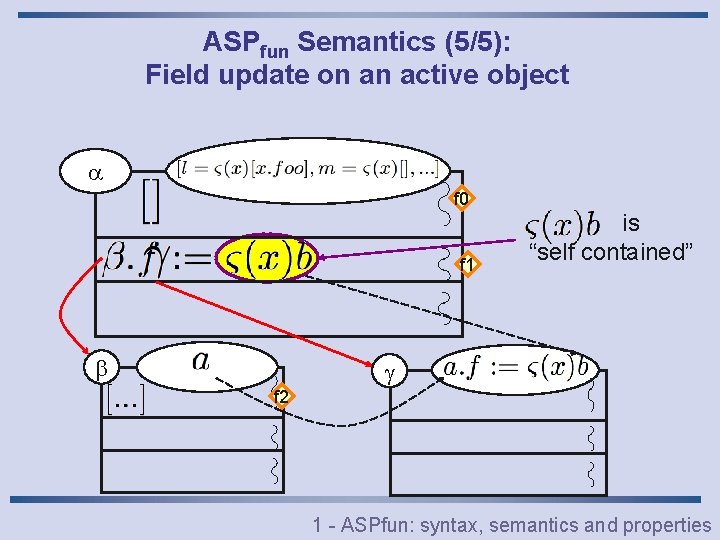
ASPfun Semantics (5/5): Field update on an active object f 0 f 1 is “self contained” f 2 1 - ASPfun: syntax, semantics and properties

A Basic Property A configuration is well-formed if it only refers to existing activities and futures Reduction preserves well-formedness Initial configuration: 1 - ASPfun: syntax, semantics and properties

Agenda 1 - ASPfun: syntax, semantics and properties 2 - A type system for ASPfun 3 - Formalization in Isabelle/HOL

Static Terms Re-uses typing for -calculus - Syntax: - Typing judgement Typing environment (mapping from variables to types) Basic idea: the type of an active object is the type of the contained object How to type active object and future references? 2 - A type system for ASPfun

Typing Configurations The type of a configuration is two mappings: - From activity to types - From futures to types A configuration is well-typed if: - Futures and activities defined in C and are the same - All the active objects of C are well-typed - All the requests of C are well-typed Then, typing terms: - -calculus terms and Active are typed as usual - Future and active object references are typed using the environment f 0 f 1 2 - A type system for ASPfun

Typing Properties Each term has a unique type Subject-reduction (reduction preserves typing) Progress: C is well-typed C can be reduced or all its requests are values Where a value is an object or a reference to an activity Absence of dead-locks 2 - A type system for ASPfun

Agenda 1 - ASPfun: syntax, semantics and properties 2 - A type system for ASPfun 3 - Formalization in Isabelle/HOL

Syntax is mostly trivial, e. g. : Finite mapping Relies on de. Bruijn indices (represent variables by natural numbers -- depth) Configurations are mappings 3 - A Formalization in Isabelle/HOL

Semantics Almost direct translation, e. g. : Like on paper, reduction relies on reduction contexts (expression with a hole: the reduction occurs in the single hole) 3 - A Formalization in Isabelle/HOL

Properties and Proofs de. Bruijn indices induce a lot of (easy) additional lemmas l Reduction preserves well-formedness (long) l Typing relatively easy to define - Proofs (subject-reduction, progress, …) relatively long but not difficult (>1000 lines each) Main difficulties: - Long repetitive proofs - A lot of design choices (e. g. define reduction contexts) - Finite maps, and associated recurrence - Two axioms remaining (fresh futures and activities exist) requires configurations as finite maps of an unbounded length l 3 - A Formalization in Isabelle/HOL

Future Works / Todo list Introduce methods with a parameter: (x, y) / a. l(b) (ongoing) Prove confluence of ASPfun - Define a parallel reduction (reducing severl terms in parallel) - ASPfun as it is specified is not confluent l l Introduce new rules for merging/garbage collecting activities Or reduce the conditions of reduction (!! progress) Remove De Bruijn indices “nominal techniques”?

Conclusion A new distributed calculus and its formalization in Isabelle A Type system: - Progress no dead-lock A base framework for developments on objects, confluence and distribution A lot of possible applications (distribution / typing / AOP …) Experiments on Isabelle (a few months development) -User-friendly, relatively fast development -Finding the right structure/representation is crucial -Proofs are long repetitive and unstructured -Difficulties when modifying / reusing code http: //www. cs. tu-berlin. de/~flokam/isabelle/sigma/

THANK YOU !!! If you prefer the Greek version …

Appendix Typing Rules Configuration ASP
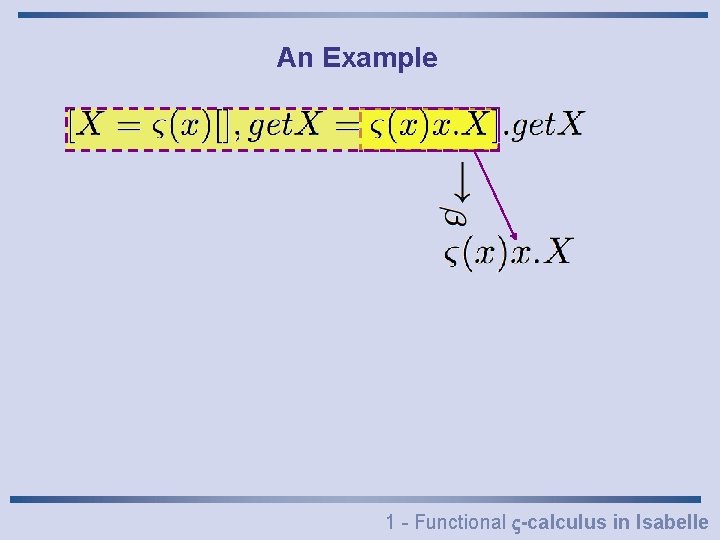
An Example 1 - Functional -calculus in Isabelle

An Example 1 - Functional -calculus in Isabelle

What are De Bruijn Indices? De Bruijn indices avoid having to deal with -conversion Variables are natural numbers depending on the depth of the parameter 1 - Functional -calculus in Isabelle

Why De Bruijn Indices? Drawbacks: l l Terms are “ugly” We are interested in general properties / not for extracting an interpreter … Lot of additional definitions/lemmas are necessary: De Bruijn indices are perhaps not the best solution - Definition subst and lift: implementation semantics more complex butofallowed a fast - Proofs of several additional (easy) lemmas Advantages l Established approach l Reuse Nipkow’s framework for confluence of the -calculus Alternative approaches, e. g. nominal techniques probably better on the long term 1 - Functional -calculus in Isabelle
- Slides: 29