ASLevel Maths Mechanics 1 Kinematics This icon indicates

AS-Level Maths: Mechanics 1 Kinematics This icon indicates the slide contains activities created in Flash. These activities are not editable. For more detailed instructions, see the Getting Started presentation. 1 of 37 © Boardworks Ltd 2005

Contents Motion graphs 2 of 37 © Boardworks Ltd 2005

Kinematics involves the study of how things move. It is only concerned with the motion itself, not the forces that cause motion. The kinematics of an object is described in terms of its distance, displacement, speed, velocity, acceleration. 3 of 37 © Boardworks Ltd 2005

Distance and displacement Distance is a scalar quantity. The distance a body has travelled is the amount of ‘ground’ it has covered during its motion. Displacement is a vector quantity. Displacement describes how far a body is from its starting point and in what direction. Distance and displacement are measured in metres, m. 4 of 37 © Boardworks Ltd 2005

Speed, velocity and acceleration Speed is a scalar quantity. The speed of a body relates to how fast the body is travelling. Velocity is a vector quantity. The velocity of a body relates to how fast the body is travelling and in what direction. It is the rate at which a body changes its position. Speed and velocity are measured in metres per second, m/s. Acceleration is a vector quantity. Acceleration is the rate of change of speed or velocity. It is measured in metres per second, m/s 2. 5 of 37 © Boardworks Ltd 2005

Motion graphs The kinematics of a body can be represented graphically. The most common graphs are position-time, velocity-time and acceleration-time graphs. The slope of a position-time graph gives velocity. The slope of a velocity-time graph gives acceleration. The area under a velocity-time graph gives the change in displacement. The area under an acceleration-time graph gives the change in velocity. The concavity of a position – time graph gives you the acceleration. The y-intercept on a position-time graph gives the initial position. 6 of 37 © Boardworks Ltd 2005

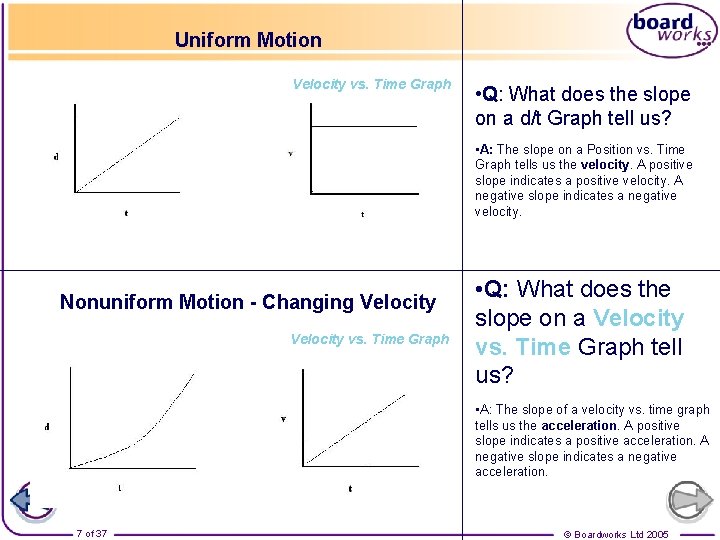
Uniform Motion Position vs. Time Graph Velocity vs. Time Graph • Q: What does the slope on a d/t Graph tell us? • A: The slope on a Position vs. Time Graph tells us the velocity. A positive slope indicates a positive velocity. A negative slope indicates a negative velocity. Nonuniform Motion - Changing Velocity Position vs. Time Graph Velocity vs. Time Graph • Q: What does the slope on a Velocity vs. Time Graph tell us? • A: The slope of a velocity vs. time graph tells us the acceleration. A positive slope indicates a positive acceleration. A negative slope indicates a negative acceleration. 7 of 37 © Boardworks Ltd 2005

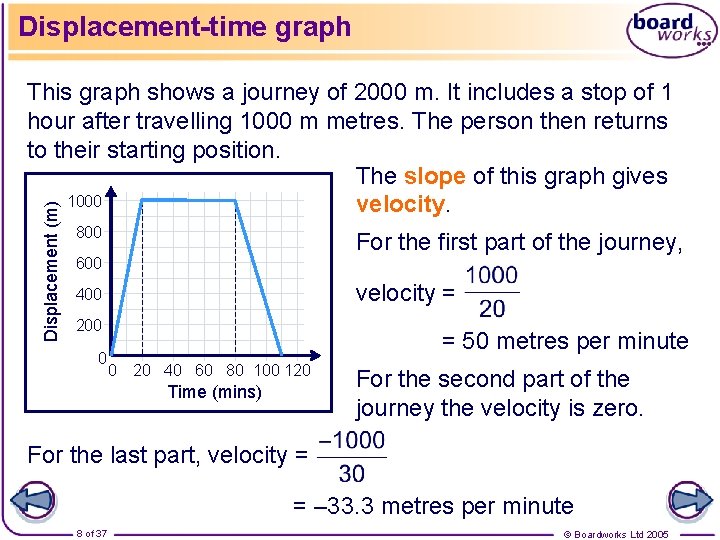
Displacement-time graph Displacement (m) This graph shows a journey of 2000 m. It includes a stop of 1 hour after travelling 1000 m metres. The person then returns to their starting position. The slope of this graph gives 1000 velocity. 800 For the first part of the journey, 600 velocity = 400 200 0 = 50 metres per minute 0 20 40 60 80 100 120 Time (mins) For the second part of the journey the velocity is zero. For the last part, velocity = = – 33. 3 metres per minute 8 of 37 © Boardworks Ltd 2005

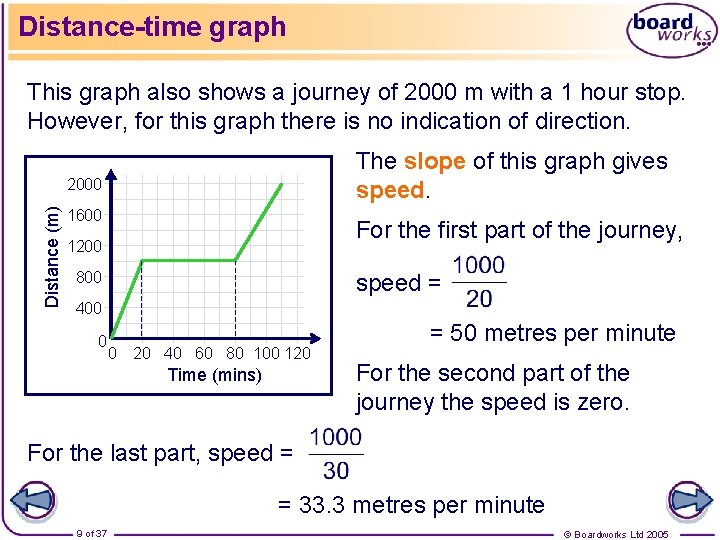
Distance-time graph This graph also shows a journey of 2000 m with a 1 hour stop. However, for this graph there is no indication of direction. The slope of this graph gives speed. Distance (m) 2000 1600 For the first part of the journey, 1200 800 speed = 400 0 0 20 40 60 80 100 120 Time (mins) = 50 metres per minute For the second part of the journey the speed is zero. For the last part, speed = = 33. 3 metres per minute 9 of 37 © Boardworks Ltd 2005

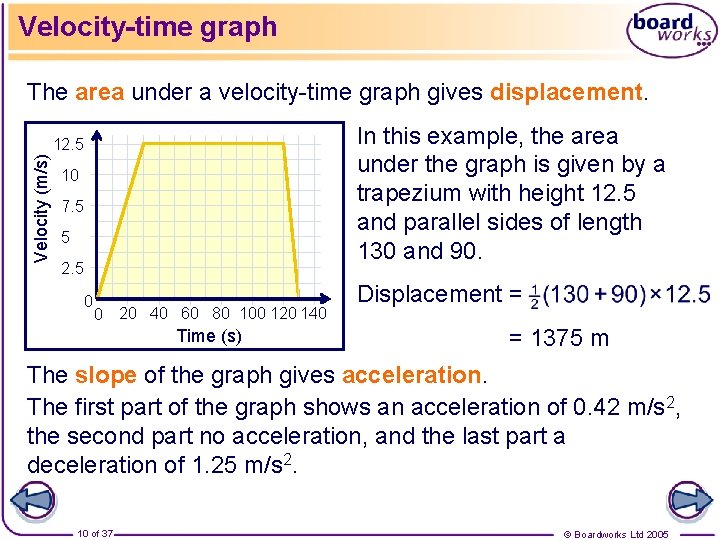
Velocity-time graph The area under a velocity-time graph gives displacement. In this example, the area under the graph is given by a trapezium with height 12. 5 and parallel sides of length 130 and 90. Velocity (m/s) 12. 5 10 7. 5 5 2. 5 0 0 20 40 60 80 100 120 140 Time (s) Displacement = = 1375 m The slope of the graph gives acceleration. The first part of the graph shows an acceleration of 0. 42 m/s 2, the second part no acceleration, and the last part a deceleration of 1. 25 m/s 2. 10 of 37 © Boardworks Ltd 2005

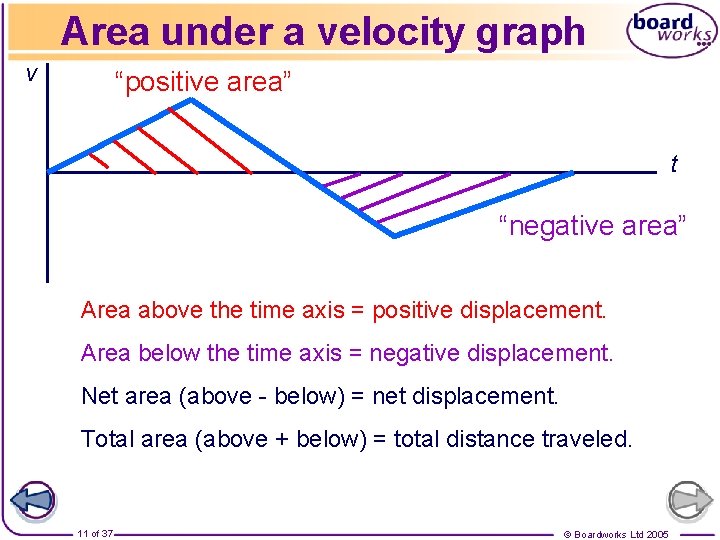
Area under a velocity graph v “positive area” t “negative area” Area above the time axis = positive displacement. Area below the time axis = negative displacement. Net area (above - below) = net displacement. Total area (above + below) = total distance traveled. 11 of 37 © Boardworks Ltd 2005

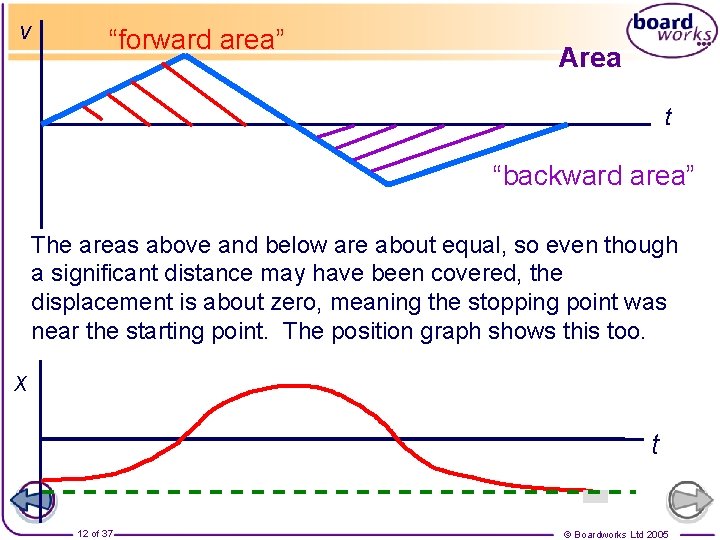
v “forward area” Area t “backward area” The areas above and below are about equal, so even though a significant distance may have been covered, the displacement is about zero, meaning the stopping point was near the starting point. The position graph shows this too. x t 12 of 37 © Boardworks Ltd 2005

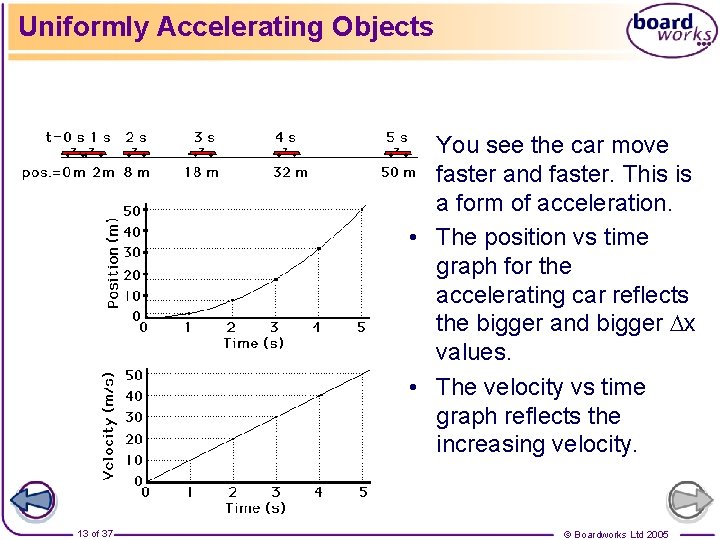
Uniformly Accelerating Objects • You see the car move faster and faster. This is a form of acceleration. • The position vs time graph for the accelerating car reflects the bigger and bigger Dx values. • The velocity vs time graph reflects the increasing velocity. 13 of 37 © Boardworks Ltd 2005

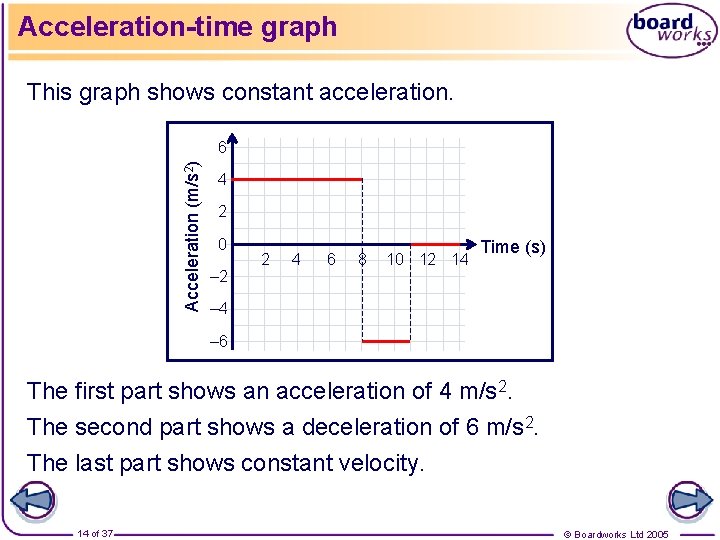
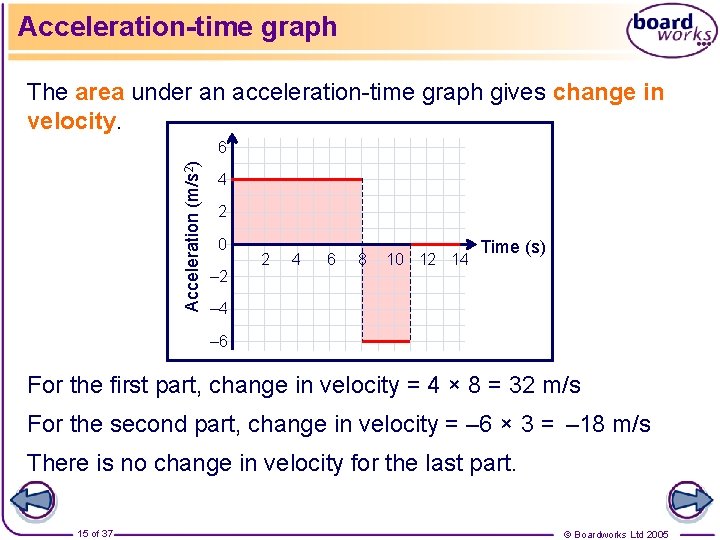
Acceleration-time graph This graph shows constant acceleration. Acceleration (m/s 2) 6 4 2 0 – 2 2 4 6 8 10 12 14 Time (s) – 4 – 6 The first part shows an acceleration of 4 m/s 2. The second part shows a deceleration of 6 m/s 2. The last part shows constant velocity. 14 of 37 © Boardworks Ltd 2005

Acceleration-time graph The area under an acceleration-time graph gives change in velocity. Acceleration (m/s 2) 6 4 2 0 – 2 2 4 6 8 10 12 14 Time (s) – 4 – 6 For the first part, change in velocity = 4 × 8 = 32 m/s For the second part, change in velocity = – 6 × 3 = – 18 m/s There is no change in velocity for the last part. 15 of 37 © Boardworks Ltd 2005

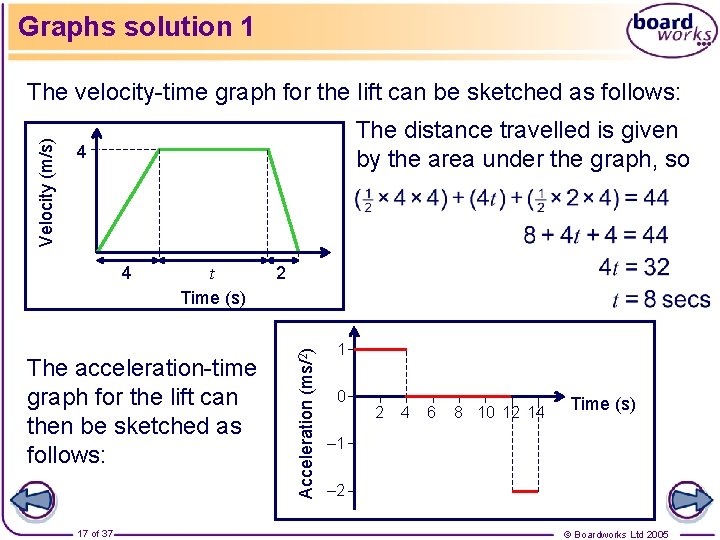
Graphs example 1 A man travels in a lift from the top floor of a hotel to reception on the ground floor. The lift accelerates with a constant acceleration of 1 m/s 2 until it reaches a constant velocity of 4 m/s. It then travels at this constant velocity for t seconds before decelerating with a constant deceleration of 2 m/s 2 until it reaches the ground floor. Given that the man has descended 44 m, a) sketch the velocity-time graph of the lift and use it to find t b) sketch the acceleration-time graph of the lift. 16 of 37 © Boardworks Ltd 2005

Graphs solution 1 The distance travelled is given by the area under the graph, so 4 4 t Time (s) The acceleration-time graph for the lift can then be sketched as follows: 17 of 37 2 Acceleration (ms/2) Velocity (m/s) The velocity-time graph for the lift can be sketched as follows: 1 0 2 4 6 8 10 12 14 Time (s) – 1 – 2 © Boardworks Ltd 2005