ASLevel Maths Mechanics 1 for Edexcel M 1

AS-Level Maths: Mechanics 1 for Edexcel M 1. 2 Vectors in mechanics These icons indicate that teacher’s notes or useful web addresses are available in the Notes Page. This icon indicates the slide contains activities created in Flash. These activities are not editable. For more detailed instructions, see the Getting Started presentation. 1 of 27 © Boardworks Ltd 2005

Definition of a vector Contents Definition of a vector Magnitude of a vector Unit vectors Multiplying vectors Addition and subtraction of vectors Examination-style questions 2 of 27 © Boardworks Ltd 2005

Definition Vectors are quantities that are completely described by a scalar magnitude and a direction. Displacement, velocity, acceleration and force can all be vectors – they can be described fully by their magnitude and direction. Vectors are often represented by a directed line segment. B This vector could be represented as: a, a or AB. A A bold letter is used to represent vectors in text books and on exam papers. When writing by hand, the convention is to underline the letter. 3 of 27 © Boardworks Ltd 2005

Column and component form A vector can be represented in component form as ai + bj in two dimensions, or ai + bj + ck in three dimensions. The vectors i, j and k are unit vectors in the positive directions of the x, y and z axes respectively. A vector can also be represented in column form æa ö ç ÷ æ aö as çç ÷÷ or çç b ÷÷. èbø ç ÷ çc ÷ è ø 4 of 27 © Boardworks Ltd 2005

Position vectors The position vector of a point A is the vector OA where O is the origin. r is often used to denote a position vector. For example, if OA = 3 i + 2 j – k, we might say r = 3 i + 2 j – k. 5 of 27 © Boardworks Ltd 2005

Magnitude of a vector Contents Definition of a vector Magnitude of a vector Unit vectors Multiplying vectors Addition and subtraction of vectors Examination-style questions 6 of 27 © Boardworks Ltd 2005

Magnitude of a vector The magnitude of a vector is the size of the vector. When representing a vector by a directed line segment, the magnitude of the vector is represented by its length. The magnitude of a vector is equal to a. The magnitude of a vector is found using Pythagoras’ Theorem. If x = ai + bj then x = x b Similarly, in three dimensions, if x = ai + bj + ck a then = 7 of 27 © Boardworks Ltd 2005

Magnitude questions Find the magnitude of the following vectors: a) 3 i + 2 j b) 4 i – 6 j + k c) -i + 3 j – 5 k d) æ - 3ö ç ÷ ç ÷ è 5ø e) æ 2ö ç ÷ ç -1÷ ç 3÷ è ø 8 of 27 © Boardworks Ltd 2005

Magnitude solutions a) Magnitude = b) Magnitude = c) Magnitude = d) Magnitude = e) Magnitude = 9 of 27 © Boardworks Ltd 2005

Unit vectors Contents Definition of a vector Magnitude of a vector Unit vectors Multiplying vectors Addition and subtraction of vectors Examination-style questions 10 of 27 © Boardworks Ltd 2005

Unit vectors A unit vector is a vector of magnitude 1. If v is a vector then the corresponding unit vector is represented by v . A unit vector in the direction of a given vector is found by v dividing the vector by the magnitude: vˆ = v 11 of 27 © Boardworks Ltd 2005

Unit vector questions Find a unit vector in the direction of the following vectors: a) 4 i – 2 j b) 3 i – j + 4 k c) – 3 i + 5 j – 2 k d) e) æ 3ö ç ÷ ç 6÷ è ø æ - 4ö ç ÷ ç 0÷ ç 3÷ è ø 12 of 27 © Boardworks Ltd 2005

Unit vector solutions 13 of 27 © Boardworks Ltd 2005

Multiplying vectors Contents Definition of a vector Magnitude of a vector Unit vectors Multiplying vectors Addition and subtraction of vectors Examination-style questions 14 of 27 © Boardworks Ltd 2005

Multiplication of a vector by a scalar To multiply a vector by a scalar, multiply each component of the vector by the scalar. 3(2 i – 5 j + k) = 6 i – 15 j + 3 k If the scalar is greater than 1, the resulting vector is larger than the original vector and parallel to it. If the scalar is less than 1, the resulting vector is smaller than the original vector and parallel to it. 15 of 27 © Boardworks Ltd 2005

Parallel vectors For vectors to be equal, the i, j and k components must be equal. One vector is the negative of another if each of their corresponding components have opposite signs. Two vectors are parallel if one is a scalar multiple of the other: 3 i – 3 j + 4 k and – 9 i + 9 j – 12 k are parallel vectors since – 9 i + 9 j – 12 k = – 3(3 i – 3 j+ 4 k) 16 of 27 © Boardworks Ltd 2005

Addition and subtraction of vectors Contents Definition of a vector Magnitude of a vector Unit vectors Multiplying vectors Addition and subtraction of vectors Examination-style questions 17 of 27 © Boardworks Ltd 2005

Addition and subtraction Adding and subtracting vectors in component form is simply a case of adding and subtracting the i, j and k components separately. Add the following vectors: 3 i + 5 j – k, 2 i + 3 k and – 4 i + 3 j + k. (3 i + 5 j – 2 k) + (2 i + 3 k) + (– 4 i + 3 j + k) = i + 8 j + 2 k 18 of 27 © Boardworks Ltd 2005

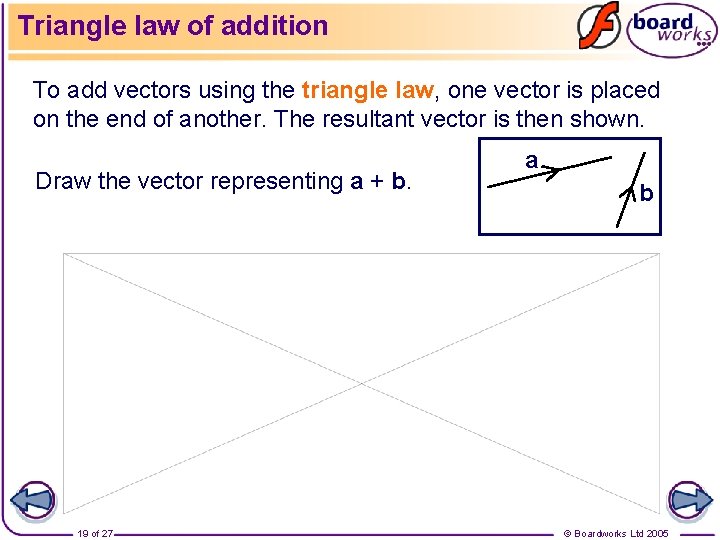
Triangle law of addition To add vectors using the triangle law, one vector is placed on the end of another. The resultant vector is then shown. Draw the vector representing a + b. 19 of 27 a b © Boardworks Ltd 2005

Parallelogram law of addition To add two vectors, a and b, using the parallelogram law, the vectors are first placed so that they both start from the same fixed point. a is then put on the end of b and b is placed at the end of a. A parallelogram is now formed – the diagonal of this is the vector a + b. a Draw the vector representing a + b. 20 of 27 b © Boardworks Ltd 2005

Examination-style questions Contents Definition of a vector Magnitude of a vector Unit vectors Multiplying vectors Addition and subtraction of vectors Examination-style questions 21 of 27 © Boardworks Ltd 2005

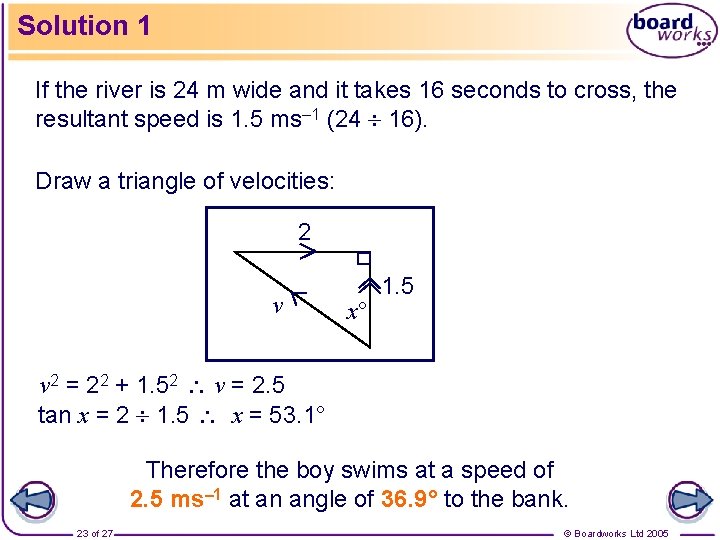
Examination-style question 1 A boy swims across a river from a point A on one bank to a point B on the other. A and B are directly opposite each other and the river is 24 metres wide. The river is flowing at 2 ms– 1 parallel to the banks. If the boy reaches point B after swimming for 16 seconds, at what speed and in what direction did he swim? 22 of 27 © Boardworks Ltd 2005

Solution 1 If the river is 24 m wide and it takes 16 seconds to cross, the resultant speed is 1. 5 ms– 1 (24 16). Draw a triangle of velocities: 2 v x° 1. 5 v 2 = 22 + 1. 52 v = 2. 5 tan x = 2 1. 5 x = 53. 1° Therefore the boy swims at a speed of 2. 5 ms– 1 at an angle of 36. 9° to the bank. 23 of 27 © Boardworks Ltd 2005

Examination-style question 2 a Two boats A and B are travelling with constant velocities. A travels with a velocity of (2 i + 4 j) kmh– 1 and B travels with a velocity of (– 2 i + 5 j) kmh– 1. a) Find the bearings on which A and B are travelling. A is moving in the first quadrant at an angle of tan– 1 2 to the horizontal. This is an angle of 63. 4° (to 3 s. f. ), so A is travelling on a bearing of 027°. B is moving in the second quadrant at an angle of tan– 1 2. 5 to the horizontal. This is an angle of 68. 2° (to 3 s. f. ), so B is travelling on a bearing of 338°. 24 of 27 © Boardworks Ltd 2005

Examination-style question 2 b and c At 2 pm, A is at point O and B is 5 km due east of O. At time t hours after 2 pm, the position vectors of A and B relative to O are a and b respectively. b) Find a and b in terms of t, i and j. a = t(2 i + 4 j) = 2 ti + 4 tj b = 5 i + t(– 2 i + 5 j) = (5 – 2 t)i + 5 tj c) At what time will A be due north of B? When A is due north of B, the i components are equal. Equating i components gives 2 t = 5 – 2 t 4 t = 5 t = 1. 25. Therefore A is due north of B at 3: 15 pm. 25 of 27 © Boardworks Ltd 2005

Examination-style question 2 d At time t hours after 2 pm the distance between the two boats is d km. d) Show that d 2 = 17 t 2 – 40 t + 25 The distance between the two boats is AB. d 2 is therefore equal to AB 2. AB = b – a = (5 – 2 t)i – 2 ti + (5 t – 4 t)j = (5 – 4 t)i + tj AB 2 = (5 – 4 t)2 + t 2 d 2 = 25 – 40 t + 16 t 2 + t 2 = 17 t 2 – 40 t + 25 26 of 27 © Boardworks Ltd 2005

Examination-style question 2 e e) At 2 pm the boats were 5 km apart. Find, correct to the nearest minute, the time when the boats are again 5 km apart. When the boats are 5 km apart, d 2 = 25. Therefore, 25 = 17 t 2 – 40 t + 25 17 t 2 – 40 t = 0 t(17 t – 40) = 0 t = 0 or t = 40 17 = 2. 35 (to 3 s. f. ), which is equivalent to 2 hours 21 minutes (to the nearest minute). Therefore the boats are again 5 km apart at 4: 21 pm. 27 of 27 © Boardworks Ltd 2005