ASD Beam Design Bending lateral stability unbalanced combination

ASD Beam Design • Bending – – lateral stability – unbalanced combination of laminations (gluelam) • Shear – • Deflection – • Bearing (for a rectangular beam)

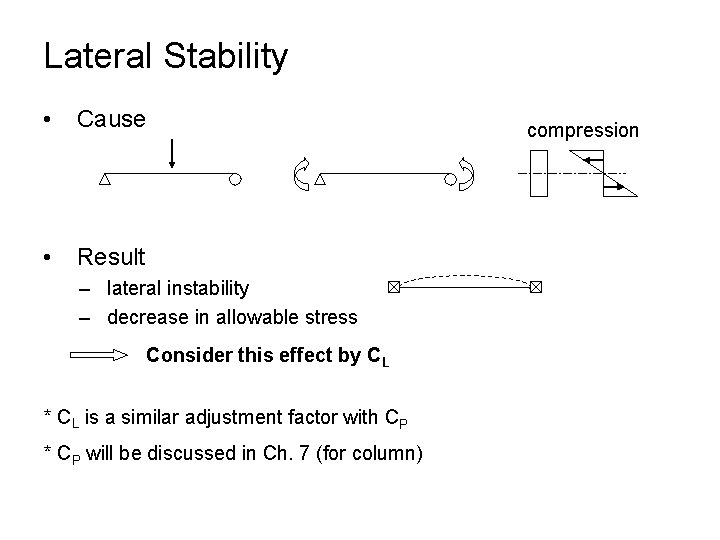
Lateral Stability • Cause • Result – lateral instability – decrease in allowable stress Consider this effect by CL * CL is a similar adjustment factor with CP * CP will be discussed in Ch. 7 (for column) compression

Lateral Stability • full lateral support – appropriate connection of a roof or diaphragm (sheathing) – lu = 0 • Approximate method b – depth-to-thickness ratio (d/b) = 6 bridging or solid blocking required at intervals of 8 ft max. d

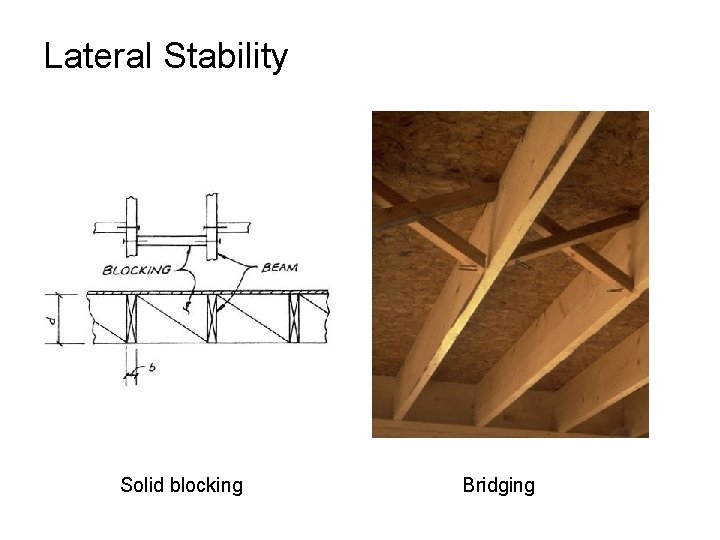
Lateral Stability Solid blocking Bridging

Lateral Stability (using CL) • Concept (Euler Buckling) – Euler critical buckling stress – Euler-based critical buckling stress Kb. E = 0. 439 for visually graded lumber = 0. 561 for MEL (machine evaluated lumber) = 0. 610 for MSR (machine stress rating) or gluelam

Lateral Stability (using CL) • Procedure of computing CL unbraced length of beam Evaluating lu Evaluating le Calculating RB b Calculating Fb. E slenderness ratio d Calculating CL

Lateral Stability (using CL) • Effective unbraced length, le

Lateral Stability (using CL) • Calculate CL - Fbx* = tabulated bending stress for x axis multiplied by adjustment factors (except Cfu, CV, and CL) - Ey’ = modulus of elasticity about y axis multiplied by adjustment factors

Lateral Stability (Example) 48’ w. TL = 1 k / ft, D+S 6. 75*37. 5 24 F-1. 8 E gluelam psi

Lateral Stability (Example) * Note Allowable Bending Stress for Strong Axis: Choose the smaller

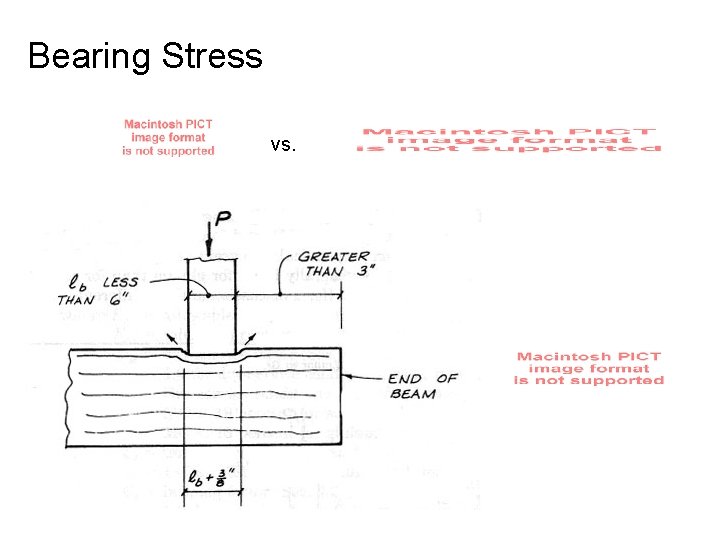
Bearing Stress vs.

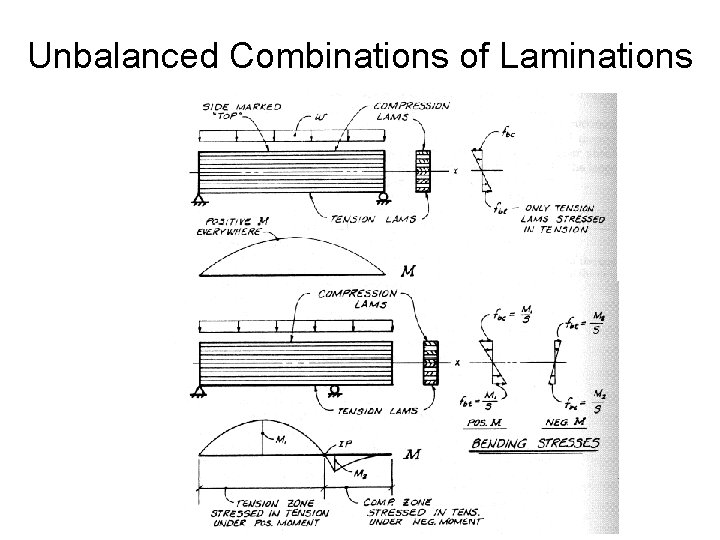
Unbalanced Combinations of Laminations