ASCII Acronym for the American Standard Code for







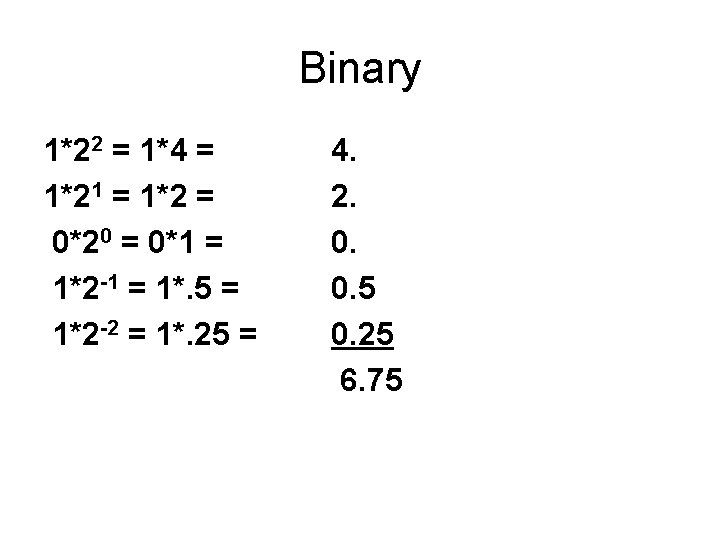





- Slides: 15

ASCII Acronym for the American Standard Code for Information Interchange. Pronounced askee, ASCII is a code for representing English characters as numbers, with each letter assigned a number from 0 to 127. For example, the ASCII code for uppercase M is 77. Most computers use ASCII codes to represent text, which makes it possible to transfer data from one computer to another. Text files stored in ASCII format are sometimes called ASCII files. Text editors and word processors are usually capable of storing data in ASCII format, although ASCII format is not always the default storage format. Most data files, particularly if they contain numeric data, are not stored in ASCII format. Executable programs are never stored in ASCII format. The standard ASCII character set uses just 7 bits for each character. There are several larger character sets that use 8 bits, which gives them 128 additional characters. The extra characters are used to represent non-English characters, graphics symbols, and mathematical symbols. Several companies and organizations have proposed extensions for these 128 characters. The DOS operating system uses a superset of ASCII called extended ASCII or high ASCII. A more universal standard is the ISO Latin 1 set of characters, which is used by many operating systems, as well as Web browsers.

bit & bytes • Short for binary digit, the smallest unit of information on a machine. The term was first used in 1946 • A single bit can hold only one of two values: 0 or 1. More meaningful information is obtained by combining consecutive bits into larger units. For example, a byte is composed of 8 consecutive bits. • Computers are sometimes classified by the number of bits they can process at one time or by the number of bits they use to represent addresses. These two values are not always the same, which leads to confusion. For example, classifying a computer as a 32 -bit machine might mean that its data registers are 32 bits wide or that it uses 32 bits to identify each address in memory. Whereas larger registers make a computer faster, using more bits for addresses enables a machine to support larger programs. • Graphics are also often described by the number of bits used to represent each dot. A 1 -bit image is monochrome; an 8 -bit image supports 256 colors or grayscales; and a 24 - or 32 -bit graphic supports true color.

EBCDIC • Abbreviation of Extended Binary-Coded Decimal Interchange Code. Pronounced eb-sih-dik, EBCDIC is an IBM code for representing characters as numbers. Although it is widely used on large IBM computers, most other computers, including PCs and Macintoshes, use ASCII codes.

Binary • Every computer processor is made of millions of tiny switches that can be turned off or on. Since these switches only have two states, it makes sense for a computer to perform its computations with a number system that only has two digits: the binary number system. These digits (0 and 1) are called bits and correspond to the off/on positions of the switches in the computer processor. With only these two digits, a computer can perform all the arithmetic calculations that the decimal system can. • Every instruction that a computer executes is coded in this binary language.

Binary • The base of any number system is determined by the number of digits in the system. For example, we know that binary is a base-2 number system since it uses two digits and decimal is a base-10 system since it uses ten digits. • A decimal number would be written like 462. 1510 and a typical binary number would be written like 110. 112.

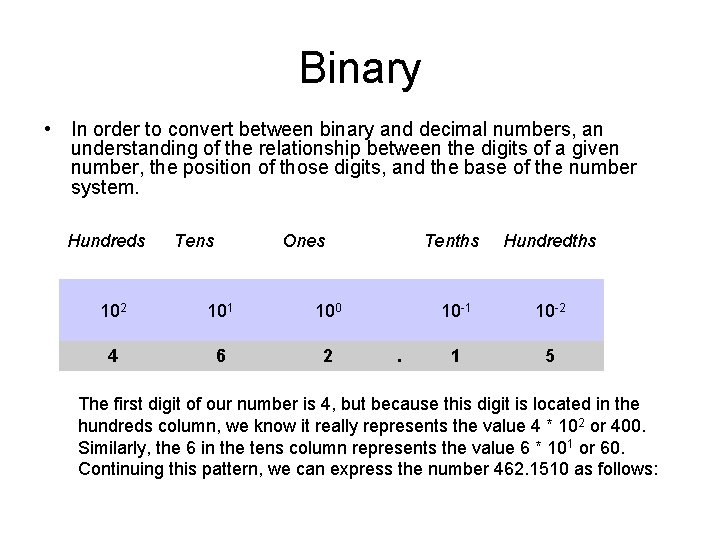
Binary • In order to convert between binary and decimal numbers, an understanding of the relationship between the digits of a given number, the position of those digits, and the base of the number system. Hundreds Tens Ones Tenths Hundredths 102 101 100 10 -1 10 -2 4 6 2 . 1 5 The first digit of our number is 4, but because this digit is located in the hundreds column, we know it really represents the value 4 * 102 or 400. Similarly, the 6 in the tens column represents the value 6 * 101 or 60. Continuing this pattern, we can express the number 462. 1510 as follows:

Number systems • In general, the relationship between a digit, its position, and the base of the number system is expressed by the following formula: • DIGIT * BASE POSITION #

• The binary system is a base-2 number system, we can make this formula more specific: DIGIT * 2 POSITION # The binary number 110. 112 in a table. Halve Fourths s Fours Twos Ones 22 21 20 2 -1 2 -2 1 1 0 . 1 1
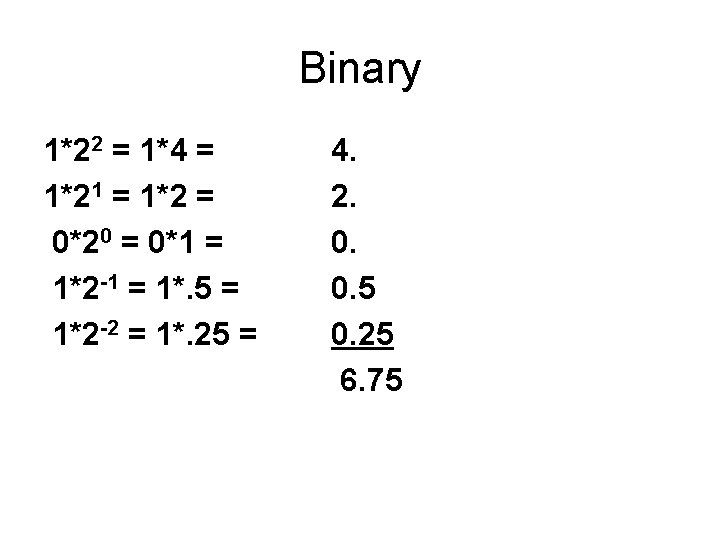
Binary 1*22 = 1*4 = 1*21 = 1*2 = 0*20 = 0*1 = 1*2 -1 = 1*. 5 = 1*2 -2 = 1*. 25 = 4. 2. 0. 0. 5 0. 25 6. 75

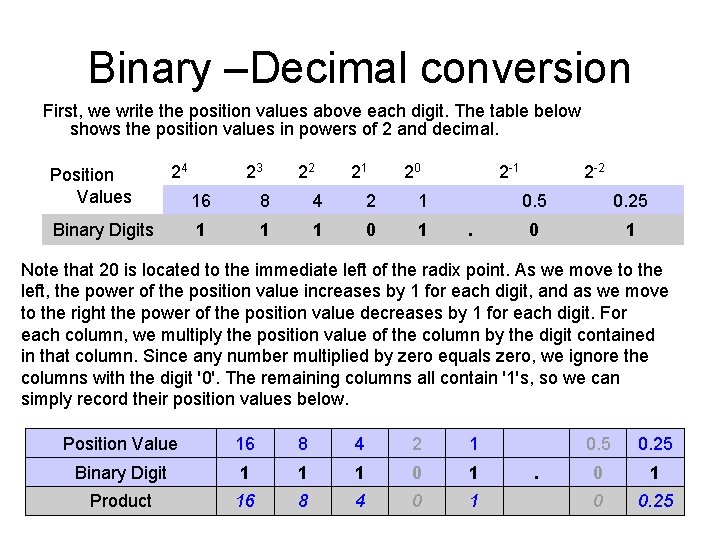
Binary –Decimal conversion First, we write the position values above each digit. The table below shows the position values in powers of 2 and decimal. Position Values 24 Binary Digits 23 22 21 20 2 -1 2 -2 16 8 4 2 1 0. 5 0. 25 1 1 1 0 1 Note that 20 is located to the immediate left of the radix point. As we move to the left, the power of the position value increases by 1 for each digit, and as we move to the right the power of the position value decreases by 1 for each digit. For each column, we multiply the position value of the column by the digit contained in that column. Since any number multiplied by zero equals zero, we ignore the columns with the digit '0'. The remaining columns all contain '1's, so we can simply record their position values below. Position Value 16 8 4 2 1 0. 5 0. 25 Binary Digit 1 1 1 0 1 Product 16 8 4 0 1 0 0. 25

Binary -decimal • Finally, we sum the values we listed to get the decimal answer. • 11101. 012 = 16 + 8 + 4 + 1 + 0. 25 = 29. 25

Binary Addition First, we add the numbers in the rightmost column. One plus zero adds to 1. 01111 + 00110 1 2. Now we add the next column. One plus one adds to 102, so we carry the one to the next column and write the zero under this column. 1 01111 + 00110 01 3. Notice that the third column now contains three ones. Adding the first two ones gives us 102. Adding this sum to the remaining one gives us a total of 112, so we carry a one to the next column and write one under this column. 1. 4. 5. 6. 11 01111 + 00110 101 The two ones in the fourth column add to 102, so we carry a one to the final column, and write zero below this column. 111 01111 + 00110 0101 Finally, the carry from the previous column plus the two zeros from this column add to 1. 111 01111 + 00110 10101 This gives us a final answer of 101012. 111 01111 + 00110 10101 Animated link

Binary Subtraction To do subtraction in the decimal system we normally use the borrow method. Consider the example problem to the right. Here we must borrow a 10 from the tens column in order to complete the subtraction in the ones column. We move 10 to the ones column and subtract 6. Then we copy down the remaining 20 from the tens column to get our answer of 24. 2(10) 30 -6 24 We can also use the borrow method to do binary subtraction. The basic rules for binary subtraction are listed in the table below. Again we see that the first three rules are similar to their decimal counterparts. The fourth rule, however, needs a little more explanation since it defines how we borrow from another column. Let's look at a simple example to see where this rule comes from. Consider the problem of subtracting 12 from 102. Rule 1 0 – 0 0 Rule 2 1 - 1 0 Rule 3 1 – 0 1 Rule 4 0 -1 1

Binary Subtraction Animated 1. To compute the first column, we need to borrow a 1 from the next column. Recall that two 1 s generated a carry in addition. If we reverse this process, we can borrow a 1 from the second column and mark two 1 s in the first column. 2. Once we borrow from the second column, we cross out the 1 and write 0 above it to show this column is now empty. The 1 from the second column is now represented by the two blue 1 s in the first column. 3. To solve our subtraction problem, we take 1 away from our group of two blue 1 s. This leaves us with a single 1 which we write below the first column. 4. After cleaning up our work, we can see that the first column of our answer is identical to Rule 4. Since we must borrow a 1 from the next column, 0 - 1 = 1 10 - 1 1 01 1 1 10 -1 1

Binary So what? GATES