AS Mathematics Algebra Graphical solution of quadratic equations

AS Mathematics Algebra – Graphical solution of quadratic equations

Objectives • Be able to factorise quadratic expressions • Be able to sketch the graph of a quadratic equation • Be able to solve quadratic equations by graphical methods

Quadratic equations When solving a quadratic equation you should always try to factorise it first. Recap: Example 1 3 x 2 - 16 x + 16 = 0 3 x 2 - 12 x - 4 x + 16 = 0 sum = -16 product = 3(16) = 48 } -4 -12 3 x(x - 4) - 4(x - 4) = 0 (x - 4)(3 x - 4) = 0 Either x - 4 = 0 or 3 x - 4 = 0 _____ x=4 or ______ x = 4/ 3 Have you checked your answer? The roots of this equation are x = 4 and x = 4/3

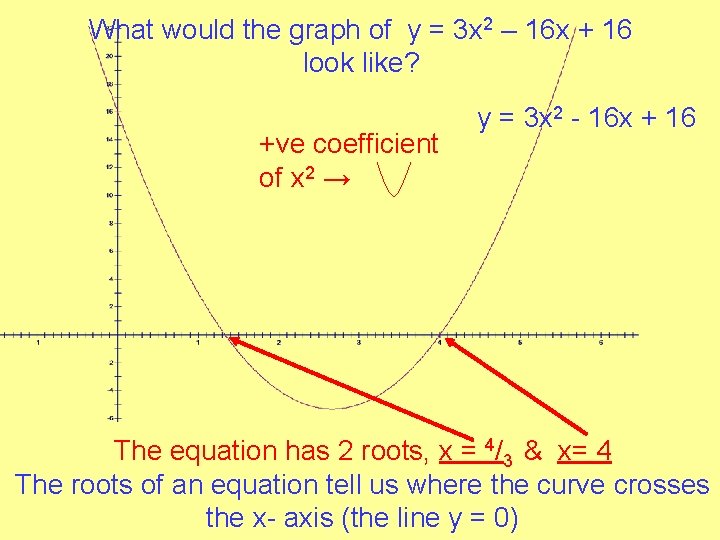
What would the graph of y = 3 x 2 – 16 x + 16 look like? +ve coefficient of x 2 → y = 3 x 2 - 16 x + 16 The equation has 2 roots, x = 4/3 & x= 4 The roots of an equation tell us where the curve crosses the x- axis (the line y = 0)

Example 2 Find the roots of the quadratic equation 3 x 2 - 6 x + 3 = 0 Use this information to draw a sketch graph of the curve y = 3 x 2 - 6 x + 3 Factorise & solve to find the roots 3 x 2 - 6 x + 3 = 0 3(x 2 - 2 x + 1) = 0 3(x - 1)2 = 0 x– 1=0 ____ x=1 The equation has one root What does this tell us about the sketch of the graph?

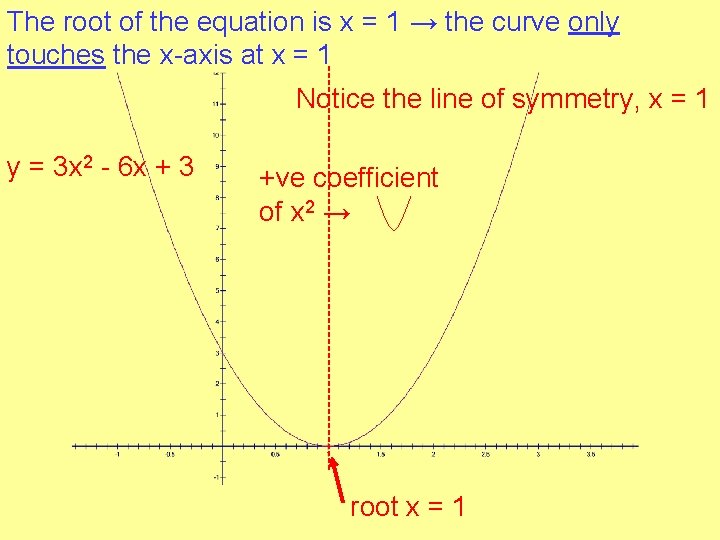
The root of the equation is x = 1 → the curve only touches the x-axis at x = 1 Notice the line of symmetry, x = 1 y = 3 x 2 - 6 x + 3 +ve coefficient of x 2 → root x = 1

Example 3 a) Draw a graph of the curve y = 2 x 2 + 3 x - 2 b) Use your graph to find an approximate solution to the equation 2 x 2 + 3 x - 12 = 0 2 x 2 + 3 x - 2 = 0 2 x 2 - x + 4 x - 2 = 0 x(2 x - 1) + 2(2 x - 1) = 0 (2 x - 1)(x + 2) = 0 2 x - 1 = 0 or x + 2 = 0 x =1/2 or x____ = -2 ____ sum = 3, product = -4 The roots of the equation are x = ½ & x = -2

The roots of the equation are x = -2 & x = ½ → the curve cuts y = 0 at x = -2 & x = ½ y = 2 x 2+ 3 x - 2 +ve coefficient of x 2 → Notice the line of symmetry, x = -11/2 root x = -2 root x = ½

b) Use your graph to find an approximate solution to the equation 2 x 2 + 3 x - 12 = 0 You need a fairly accurate graph to find the solutions of equations. Draw it by hand on graph paper, or use a graphing package / graphical calculator. Compare the quadratic we’ve just drawn, y = 2 x 2 + 3 x - 2 Rearrange with 2 x 2 + 3 x - 12 = 0 so that the LHS reads 2 x 2 + 3 x - 2 = …. . We get 2 x 2 + 3 x - 2 = 10 On the same graph as y = 2 x 2 + 3 x – 2 draw the graph of y = 10.

Where the two lines cross y = 2 x 2 + 3 x - 2 = 0 AND y = 10. In other words 2 x 2 + 3 x - 2 = 10 or 2 x 2 + 3 x - 12 = 0 y = 10 y = 2 x 2 + 3 x - 2 The graph shows 2 roots to the equation x = -3. 3 & x = 1. 8 (approximately)