Artificial Intelligence Lecture 5 Informed Search Dr Muhammad

Artificial Intelligence Lecture 5 – Informed Search Dr. Muhammad Adnan Hashmi 1/25/2022 1

Best-First Search q q Idea: use an evaluation function for each node Ø Estimate of desirability Expand most desirable unexpanded node Implementation: Ø fringe is a queue sorted in decreasing order of desirability Special cases: Ø Uniform Cost Search (uninformed) Ø Greedy (best-first) Search (informed) Ø A* Search (informed) 1/25/2022 2

Evaluation Function q q Evaluation function f(n) = g(n) + h(n) Ø g(n) = exact cost so far to reach n Ø h(n) = estimated cost to goal from n Ø f(n) = estimated total cost of cheapest path through n to goal Special cases: Uniform Cost Search: f(n) = g(n) Ø Greedy (best-first) Search: f(n) = h(n) Ø A* Search: f(n) = g(n) + h(n) Ø

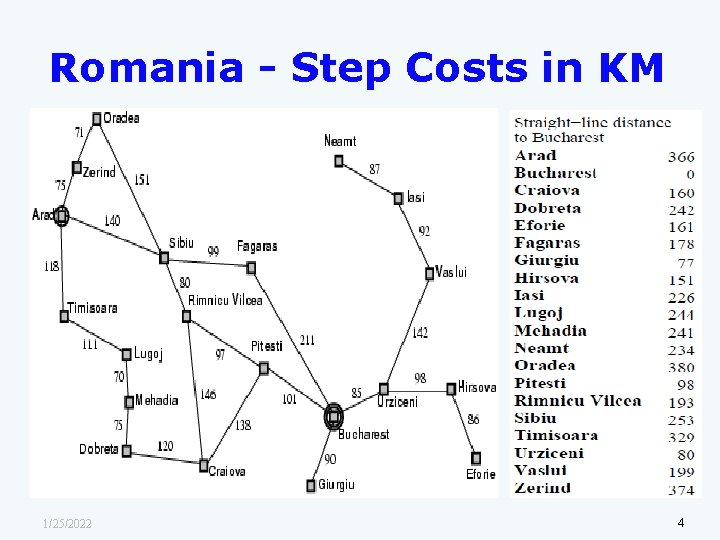
Romania - Step Costs in KM 1/25/2022 4

Greedy Best-First Search q q q Evaluation function h(n) (heuristic) Ø Estimated cost of the cheapest path from n to a goal node E. g. , h. SLD(n) = straight-line distance from n to Bucharest Greedy search expands the node that appears to be closest to goal. 1/25/2022 5

Greedy Best-First search example

Greedy Best-First search example

Greedy Best-First search example

Greedy Best-First search example 1/25/2022 9

Properties of Greedy Best-First search q q Complete? No – can get stuck in loops, e. g. , with Oradea as goal and start from Iasi: Ø Iasi Neamt Ø Complete in finite space with repeated state checking Time? O(bm), but a good heuristic can give dramatic improvement q Space? O(bm) -- keeps all nodes in memory q Optimal? No.

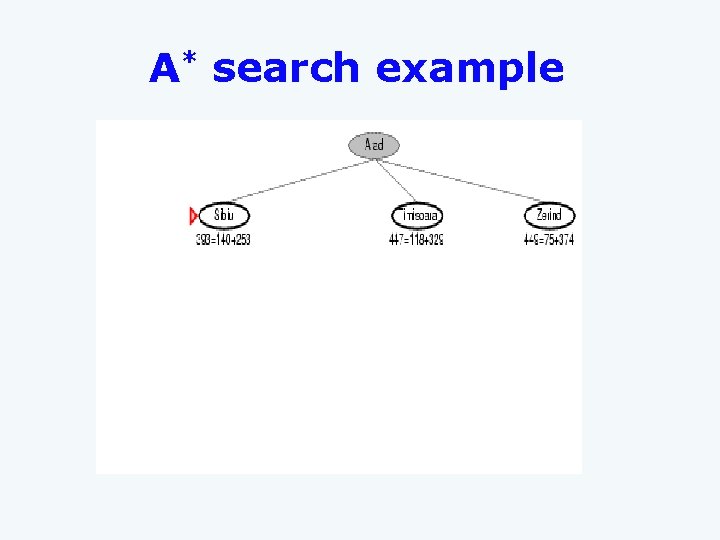
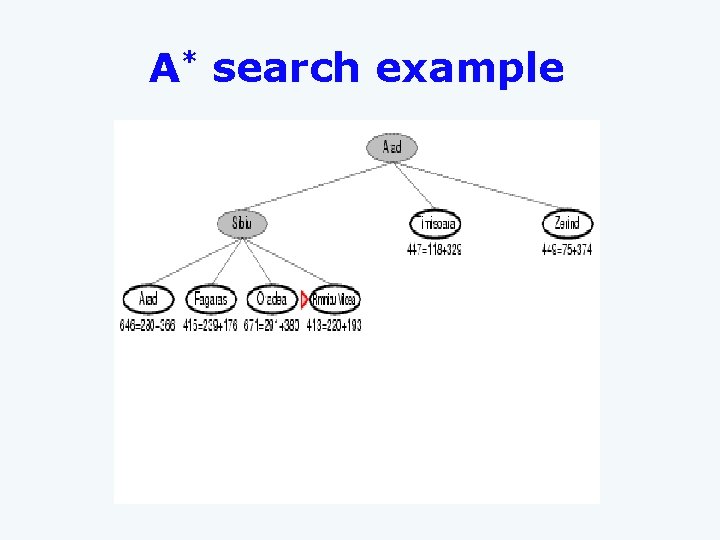
A* Search q q q Idea: Avoid expanding paths that are already expensive Evaluation function f(n) = g(n) + h(n) Ø g(n) = exact cost so far to reach n Ø h(n) = estimated cost to goal from n Ø f(n) = estimated total cost of cheapest path through n to goal A* search uses an admissible heuristic: Ø h(n) ≤ h*(n) where h*(n) is the true cost from n Ø Also h(n) ≥ 0, and h(G)=0 for any goal G Ø E. g. , h. SLD(n) is an admissible heuristic because it doesn’t overestimate the actual road distance. 1/25/2022 11

A* Search q q If we are trying to find the cheapest solution, a reasonable thing to try first is the node with the lowest value of g(n) + h(n) This strategy is more than just reasonable Ø Provided that h(n) satisfies certain conditions, A* using TREE search is both complete and optimal. 1/25/2022 12

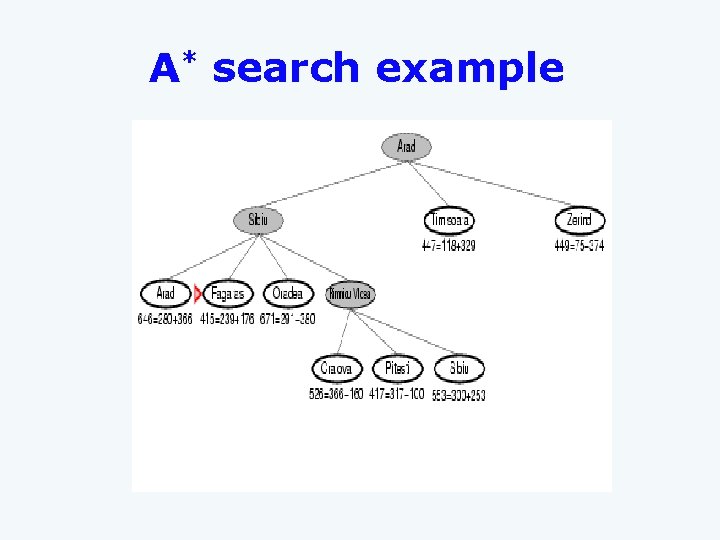
A* search example

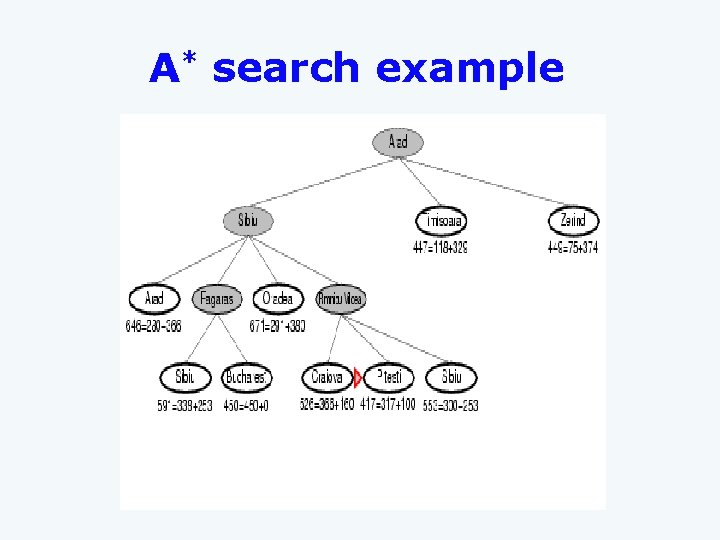
A* search example

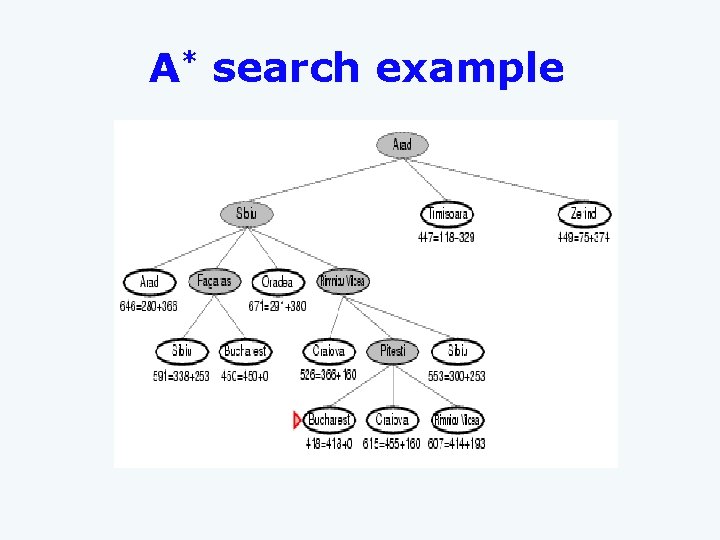
A* search example

A* search example

A* search example

A* search example

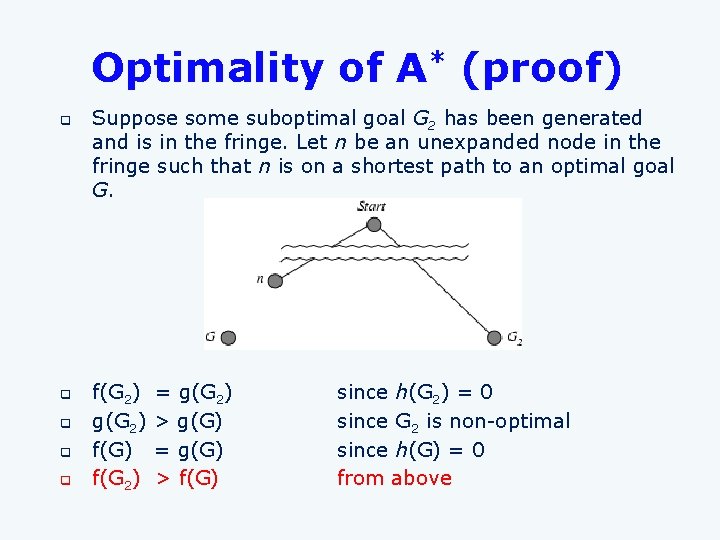
Optimality of A* (proof) q q q Suppose some suboptimal goal G 2 has been generated and is in the fringe. Let n be an unexpanded node in the fringe such that n is on a shortest path to an optimal goal G. f(G 2) g(G 2) f(G 2) = g(G 2) > g(G) = g(G) > f(G) since h(G 2) = 0 since G 2 is non-optimal since h(G) = 0 from above

Optimality of A* (proof) q q q Suppose some suboptimal goal G 2 has been generated and is in the fringe. Let n be an unexpanded node in the fringe such that n is on a shortest path to an optimal goal G. f(G 2) > f(G) from above h(n) ≤ h*(n) since h is admissible g(n) + h(n)≤ g(n) + h*(n) f(n) ≤ f(G) Hence f(G 2) > f(n), and A* will never select G 2 for expansion

Questions 1/25/2022 29