Artificial Intelligence Lecture 13 Constraint Satisfaction Problems Dr

Artificial Intelligence Lecture 13 – Constraint Satisfaction Problems Dr. Muhammad Adnan Hashmi 2/2/2022 1

Outline q q q Constraint Satisfaction Problems (CSP) Backtracking search for CSPs Local search for CSPs 2

Constraint Satisfaction Problems (CSPs) q q Standard search problem: State is a "black box“ – any data structure that supports a successor function, heuristic function, and goal test CSP: state is defined by variables Xi with values from domain Di Ø Goal test is a set of constraints specifying allowable combinations of values for subsets of variables Simple example of a formal representation language Allows useful general-purpose algorithms with more power than standard search algorithms 3

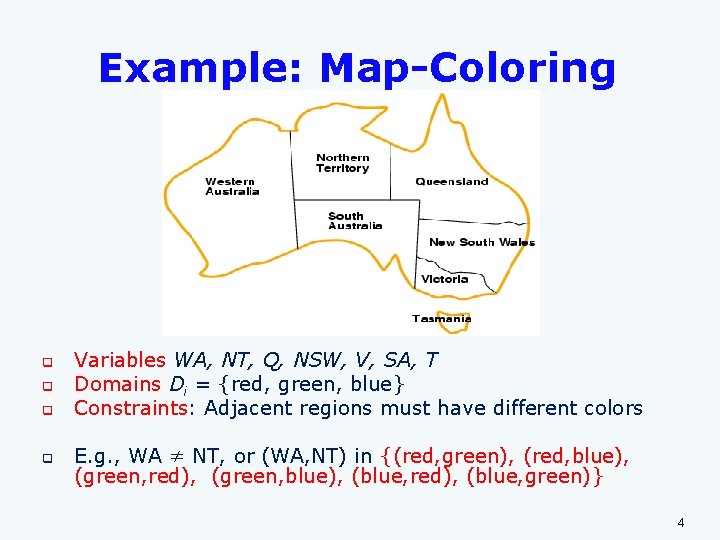
Example: Map-Coloring q q Variables WA, NT, Q, NSW, V, SA, T Domains Di = {red, green, blue} Constraints: Adjacent regions must have different colors E. g. , WA ≠ NT, or (WA, NT) in {(red, green), (red, blue), (green, red), (green, blue), (blue, red), (blue, green)} 4

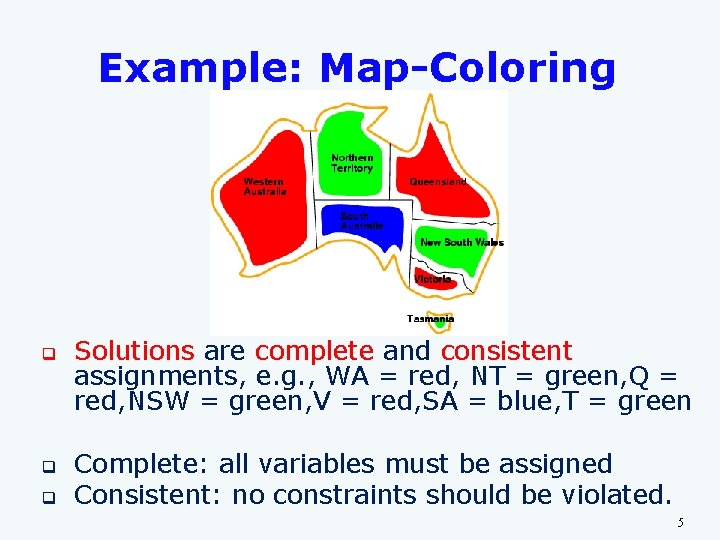
Example: Map-Coloring q q q Solutions are complete and consistent assignments, e. g. , WA = red, NT = green, Q = red, NSW = green, V = red, SA = blue, T = green Complete: all variables must be assigned Consistent: no constraints should be violated. 5

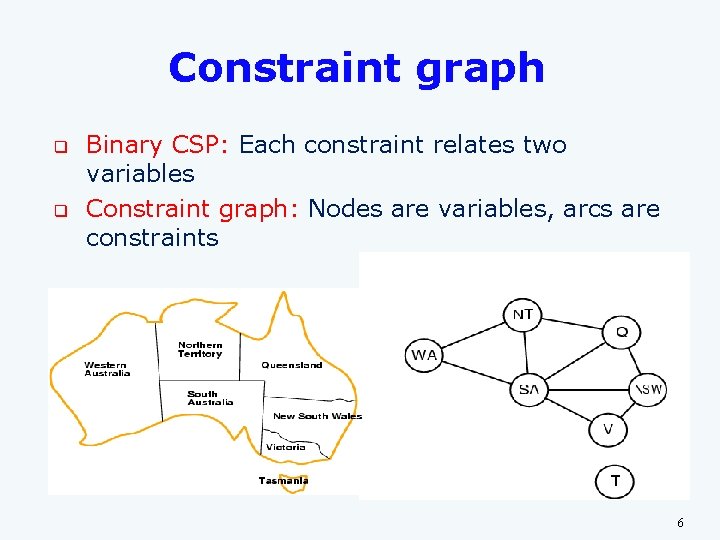
Constraint graph q q Binary CSP: Each constraint relates two variables Constraint graph: Nodes are variables, arcs are constraints 6

Varieties of CSPs q Discrete variables Ø Finite domains: § n variables, domain size d O(dn) complete assignments § e. g. , Boolean CSPs for NP-complete problems Ø Infinite domains: § integers, strings, etc. § E. g. , job scheduling: start/end days for each job § Rather than enumerating all possible variable combination, we need a constraint language, e. g. , Start. Job 1 + 5 ≤ Start. Job 3 q Continuous variables: very common in real-world E. g. , start/end times for Hubble Space Telescope observations Ø Linear constraints (inequalities) are solvable in polynomial time by linear programming Ø 7

Varieties of constraints q Unary constraints involve a single variable, Ø q Binary constraints involve pairs of variables, Ø q E. g. , SA ≠ green E. g. , SA ≠ WA Higher-order constraints involve 3 or more variables Ø E. g. , crypt-arithmetic column constraints 8

Crypt-Arithmetic q A mathematical puzzle in which each letter represents a digit (for example, if X=3, then XX=33) The object is to find the value of each letter Constraints: Ø No two letters represent the same digit (If X=3, Y cannot be 3). Ø And the first letter cannot be 0 (Given the value ZW, Z cannot be 0). q They can be quite challenging, often involving many steps q Solver Program: http: //bach. istc. kobeu. ac. jp/llp/crypt. html q q 2/2/2022 9

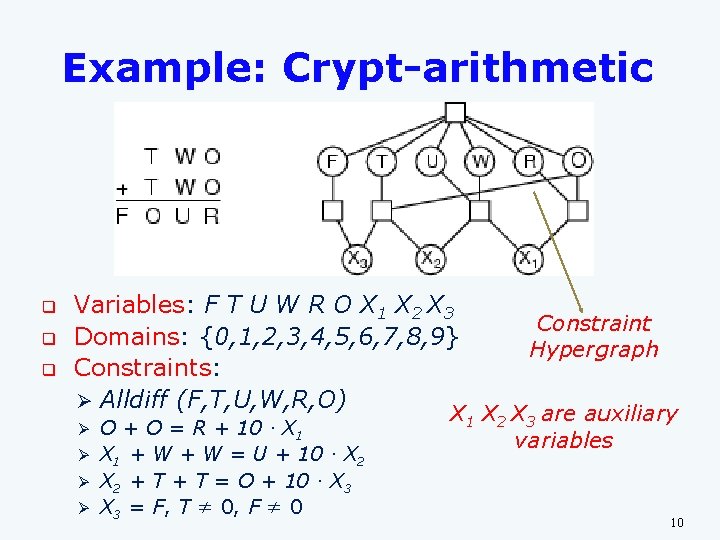
Example: Crypt-arithmetic q q q Variables: F T U W R O X 1 X 2 X 3 Domains: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} Constraints: Ø Alldiff (F, T, U, W, R, O) O + O = R + 10 · X 1 Ø X 1 + W = U + 10 · X 2 Ø X 2 + T = O + 10 · X 3 Ø X 3 = F, T ≠ 0, F ≠ 0 Ø Constraint Hypergraph X 1 X 2 X 3 are auxiliary variables 10

Important Result q q Every higher-order, finite-domain constraint can be broken down into a set of binary constraints, if enough auxiliary variables are introduced E. g. , F ≠ T, F ≠ U etc. 11

Real-world CSPs q Teacher Assignment problems, e. g. , who teaches what class q Timetabling problems, e. g. , which class is offered when and where? q q Transportation scheduling, e. g. , which transport should be scheduled for delivery at a given location Notice that many real-world problems involve real-valued variables 12

Standard Search Formulation (incremental) q States are defined by the values assigned so far: Ø Initial state: the empty assignment { } Ø Successor function: Assign a value to an unassigned variable that does not conflict with current assignment: this fails if there are no legal assignments Ø Goal test: the current assignment is complete and consistent q This is the same for all CSPs q Every solution appears at depth n with n variables use depth-first search q Path is irrelevant, so we can also use complete-state formulation. 13

Backtracking search q q Variable assignments are commutative}, i. e. , [ WA = red then NT = green ] same as [ NT = green then WA = red ] We only need to consider assignments to a single variable at each node Ø Otherwise, we will have n! dn leaves, rather than only dn leaves (which are the total no. of complete assignments) q Depth-first search for CSPs with single-variable assignments is called backtracking search q Backtracking search is the basic uninformed algorithm for CSPs q Can solve n-queens for n ≈ 25 14

Backtracking search 15

Backtracking example 16

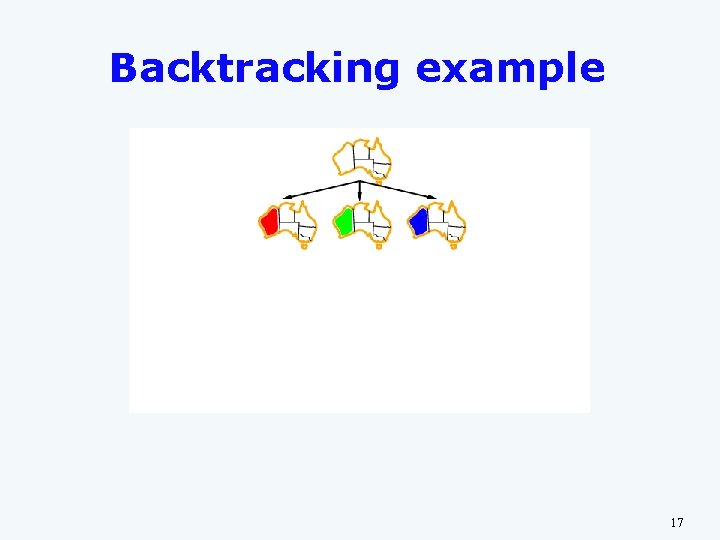
Backtracking example 17

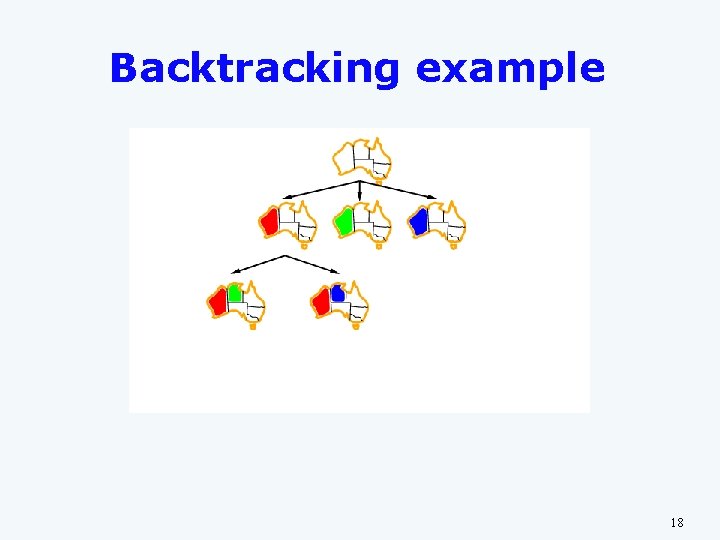
Backtracking example 18

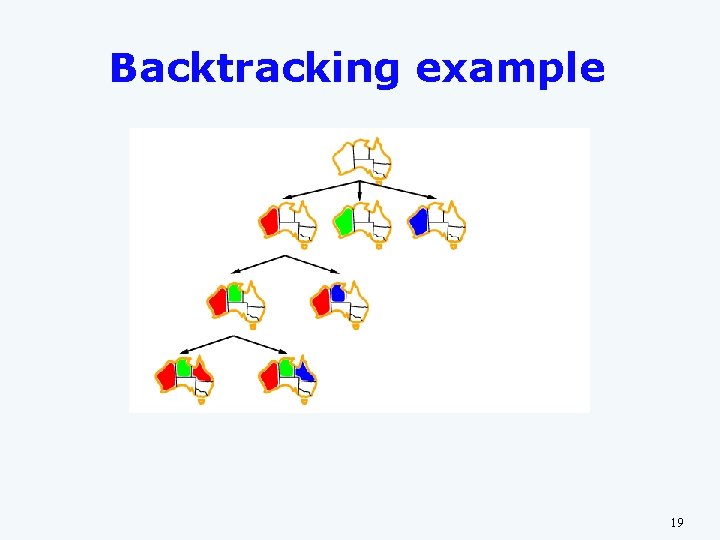
Backtracking example 19

Improving backtracking efficiency q q Pure backtracking is typically inefficient, because it is an uninformed algorithm We can think of heuristics but instead, we use three general-purpose methods: Can give huge gains in speed: Ø Which variable should be assigned next? Ø In what order should its values be tried? Ø Can we detect inevitable failure early? 20

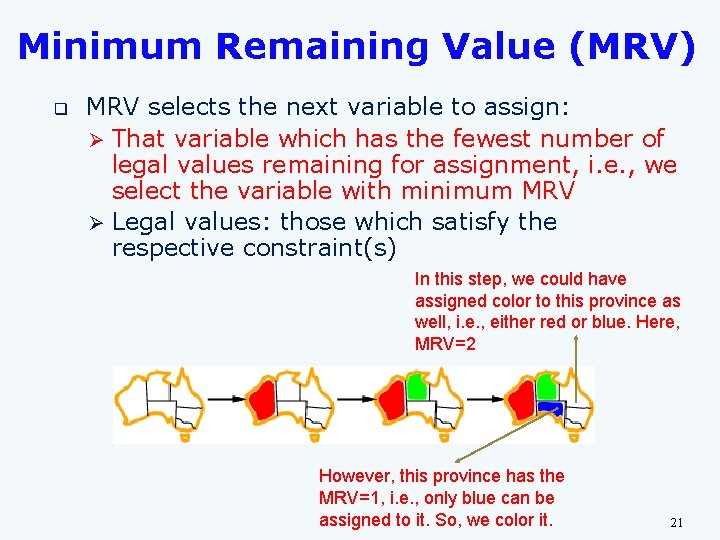
Minimum Remaining Value (MRV) q MRV selects the next variable to assign: Ø That variable which has the fewest number of legal values remaining for assignment, i. e. , we select the variable with minimum MRV Ø Legal values: those which satisfy the respective constraint(s) In this step, we could have assigned color to this province as well, i. e. , either red or blue. Here, MRV=2 However, this province has the MRV=1, i. e. , only blue can be assigned to it. So, we color it. 21

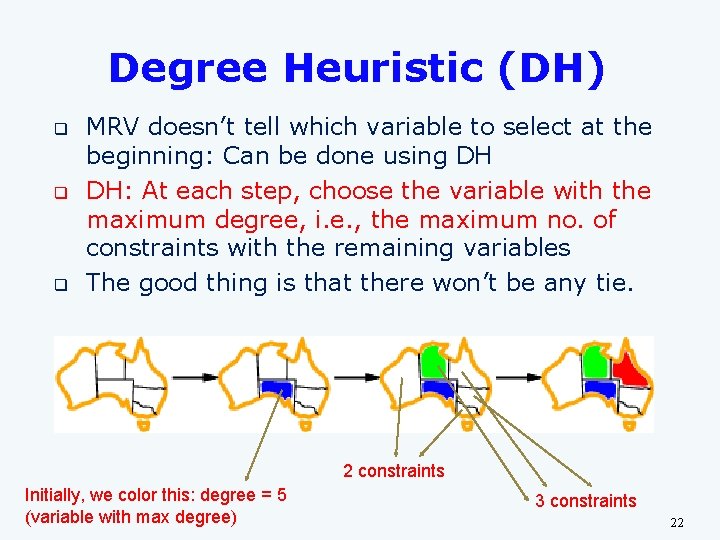
Degree Heuristic (DH) q q q MRV doesn’t tell which variable to select at the beginning: Can be done using DH DH: At each step, choose the variable with the maximum degree, i. e. , the maximum no. of constraints with the remaining variables The good thing is that there won’t be any tie. 2 constraints Initially, we color this: degree = 5 (variable with max degree) 3 constraints 22

Least Constraining Value (LCV) q q q MRV and DH concentrate on choosing variables LCV is concerned with choosing the values of variables Given a variable, choose its LCV: the one that rules out the fewest values in the remaining variables Ø The one that imposes minimum constraints on the remaining variables. SA SA can’t be assigned any color now. 23

Questions 2/2/2022 24