Artificial Intelligence Fuzzy logic Fall 2008 professor Luigi

Artificial Intelligence Fuzzy logic Fall 2008 professor: Luigi Ceccaroni

Uncertainty - Modeling with uncertainty requires more than probability theory. - There are problems where boundaries are gradual. Examples: • What is the boundary of Spain? What is the area of Spain? • When does a tumor begin its formation? • What is the habitat of rabbits? • What is the depth of the sea 30 km east of Barcelona?

Representing vagueness: Fuzzy sets and fuzzy logic • Fuzzy set theory is a means of specifying how well an object satisfies a vague description. • Example: – Consider the proposition “Carla is tall”. – Is this true, if Carla is 1. 70? – Most people would hesitate to answer “true” or “false”, preferring to say “sort of”. • This is not necessarily a question of uncertainty about the external world. – We are sure of Carla’s height.

Representing vagueness: Fuzzy sets and fuzzy logic • The linguistic term “tall” does not refer to a sharp demarcation of objects into two classes. • There are degrees of tallness. • Fuzzy set theory treats Tall as a fuzzy predicate and says that the truth value of Tall(Carla) is a number between 0 and 1, rather than being just true or false.

Representing vagueness: Fuzzy sets and fuzzy logic • The name “fuzzy set” derives from the interpretation of the predicate as implicitly defining a set of its members. • A set that does not have sharp boundaries. • Fuzzy logic is a method for reasoning with logical expressions describing membership in fuzzy sets. • Example: – The complex sentence Tall(Carla) ∧ Heavy(Carla) has a fuzzy truth value that is a function of the truth values of its components.

Examples § In classical sets, either an element belongs or it does not. Examples: § § § Set of integers – a real number is an integer or not. You are either in an airplane or not. Your bank-account balance is 142 € or not. The Bible is either the word of God, or it is not. Either Christ was divine, or he was not. § Fuzzy sets are sets that have gradations of belonging. Examples: BIG Near Tall

Degrees of truth: example • The temperature is pleasant. • Variable: temperature • Universe of values (U) or domain: real • The distribution indicates the degree of truth of the linguistic term pleasant. 1 0 0 20 30 40 ºC

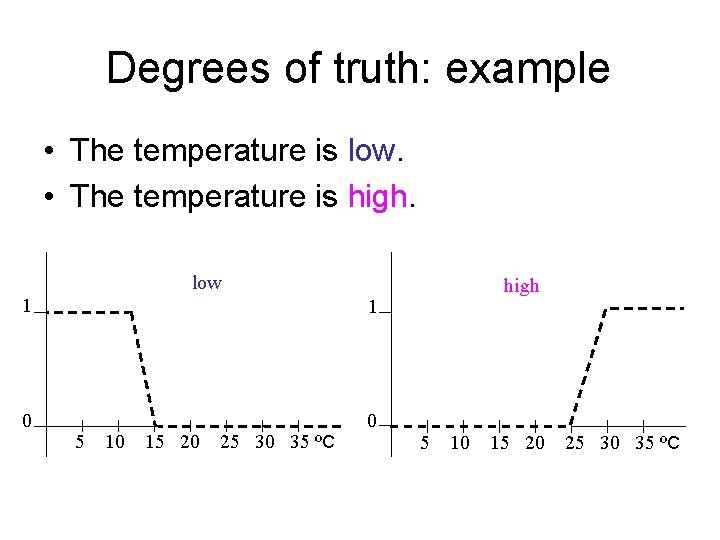
Degrees of truth: example • The temperature is low. • The temperature is high. low 1 1 0 0 5 10 15 20 25 30 35 ºC high 5 10 15 20 25 30 35 ºC

Possibility function πA : U → [0, 1] The possibility function, or characteristic function, is often represented as a trapezoidal or triangular approximation, which can be characterized by the abscises of the vertexes. 1 0 (0, 20, 30, 40) 1 0 20 30 40 0 0 20 30 40

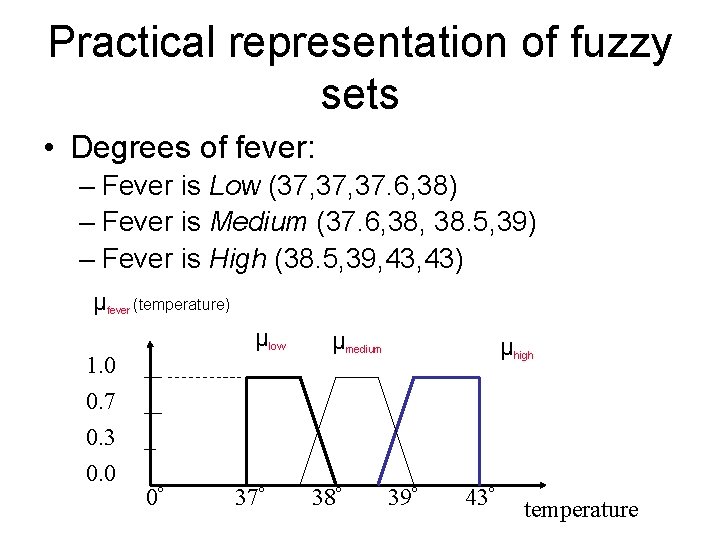
Practical representation of fuzzy sets • Degrees of fever: – Fever is Low (37, 37. 6, 38) – Fever is Medium (37. 6, 38. 5, 39) – Fever is High (38. 5, 39, 43) μfever (temperature) 1. 0 0. 7 0. 3 0. 0 μlow 0º 37º μmedium 38º μhigh 39º 43º temperature

Practical representation of fuzzy sets G 1 0 MF F 0 FS A C MC 5 10 15 20 25 30 35 • [Temperature is Gelada] • [Temperature is Molt Freda] • [Temperature is Fresca] • [Temperature is Agradable] • [Temperature is Calorosa] • [Temperature is Molt Calorosa] Each variable has a domain and a set of labels or linguistic terms. • Each label corresponds to a characteristic function defined over the domain. •

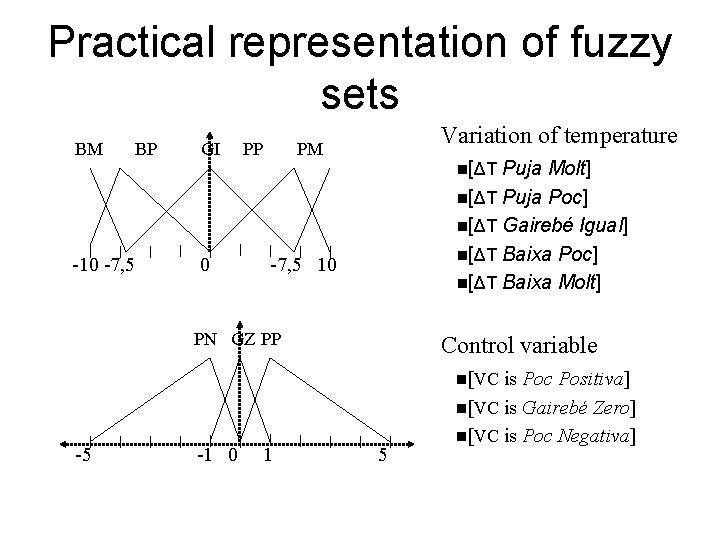
Practical representation of fuzzy sets BM BP -10 -7, 5 GI 0 PP Variation of temperature PM n[ΔT Puja Molt] n[ΔT Puja Poc] n[ΔT Gairebé Igual] n[ΔT Baixa Poc] n[ΔT Baixa Molt] -7, 5 10 PN GZ PP Control variable n[VC is -5 -1 0 1 5 Poc Positiva] n[VC is Gairebé Zero] n[VC is Poc Negativa]

Fuzzy logic: connectives • Fuzzy logical connectives are defined as functions in the [0, 1] interval, which generalize classic connectives: Intersection of sets ≡ P ∧ Q ≡ T-norm (P, Q) Union of sets ≡ P ∨ Q ≡ T-conorm (P, Q) Complement of a set ≡ ¬P ≡ Negation function (P) Inclusion of sets ≡ P → Q ≡ Implication function (P, Q) 13

Fuzzy negation • “Negation function” N : [0, 1] → [0, 1] • • Properties • N(0) = 1 and N(1) = 0 • N(p) ≥ N(q) if p ≤ q • N(N(p)) = p Examples • N(x) = 1 -x • Nw(x) = (1 -xw)1/w • Nt(x) = (1 -x) / (1+t*x) boundary conditions monotony involution ∀ w > 0 Yager family ∀ t > -1 Sugeno family 14

Fuzzy conjunction • “T-Norms” • • Properties • T(p, q) • T(p, T(q, r)) • T(p, q) • T(0, p) • T(1, p) T : [0, 1] x [0, 1] → [0, 1] = = ≤ = = T(q, p) commutability T(T(p, q), r) associativity Τ(r, s) if p ≤ r ∧ q ≤ s monotony T(p, 0) = 0 absorbing element T(p, 1) = p neutral element Examples • T(x, y) = min (x, y) • T(x, y) = x*y • T(x, y) = max (0, x+y-1) • T(x, y) = x*y / (x+y-x*y) minimum algebraic product bounded difference 15

Fuzzy disjunction • “T-Conorms” • • Properties • S(p, q) • S(p, S(q, r)) • S(p, q) • S(0, p) • S(1, p) S : [0, 1] x [0, 1] → [0, 1] = = ≤ = = S(q, p) commutability S(S(p, q), r) associativity S(r, s) if p ≤ r ∧ q ≤ s monotony S(p, 0) = p neutral element S(p, 1) = 1 absorbing element Examples • S(x, y) = max (x, y) • S(x, y) = x+y-x*y • S(x, y) = min (x+y, 1) • S(x, y) = (x+y -2 x*y) / (1 -x*y) maximum algebraic sum bounded sum 16

Relations between T-norms and T-conorms • De Morgan laws: N(T(x, y)) = S(N(x), N(y)) N(S(x, y)) = T(N(x), N(y)) • • T(x, y) = min (x, y) T(x, y) = x*y T(x, y) = max (0, x+y-1) T(x, y) = x*y / (x+y-x*y) S(x, y) = max (x, y) S(x, y) = x+y - x*y S(x, y) = min (x+y, 1) S(x, y) = (x+y -2 x*y) / (1 -x*y) 17

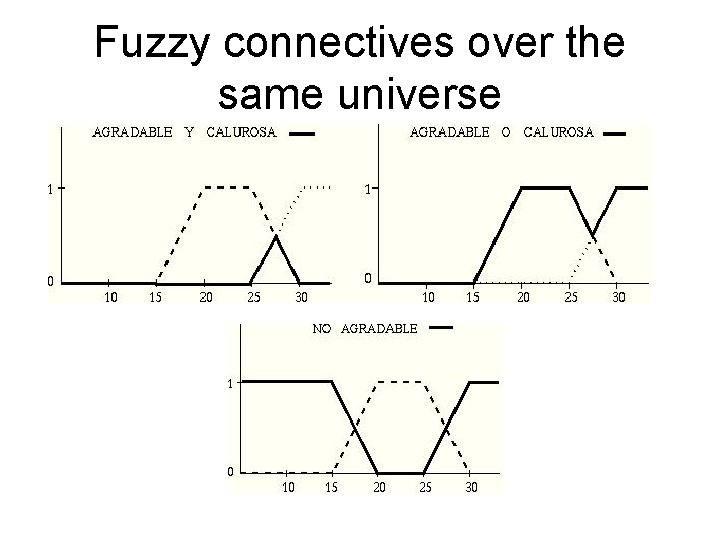
Fuzzy connectives over the same universe • If F ≡ [X is A] and G ≡ [X is B] with possibility distributions ΠA and ΠB defined over the same universe U: F ∧ G ≡ [X is A ∧ B] with ΠA∧B(u) = T(ΠA(u) , ΠB(u)) T-norm F ∨ G ≡ [X is A ∨ B] with ΠA∨ B(u) = S(ΠA(u) , ΠB(u)) T-conorm ¬ F ≡ [X is ¬ A] with Π¬ A(u) = N(ΠA(u)) Negation function 18

Fuzzy connectives over the same universe

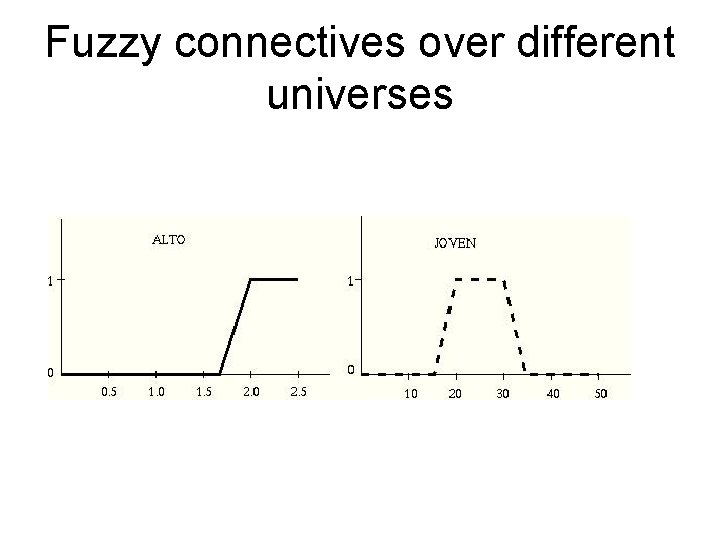
Fuzzy connectives over different universes • If F ≡ [X is A] and G ≡ [Y is B] with possibility distributions ΠA defined over U i ΠB defined over V, U≠V: F ∧ G ≡ [X is A] ∧ [Y is B] with ΠA∧B(u, v) = T(ΠA(u) , ΠB(v)) T-norm F ∨ G ≡ [X is A] ∨ [Y is B] with ΠA∨ B(u, v) = S(ΠA(u) , ΠB(v)) T-conorm Functions are defined in two different dimensions. 20

Fuzzy connectives over different universes

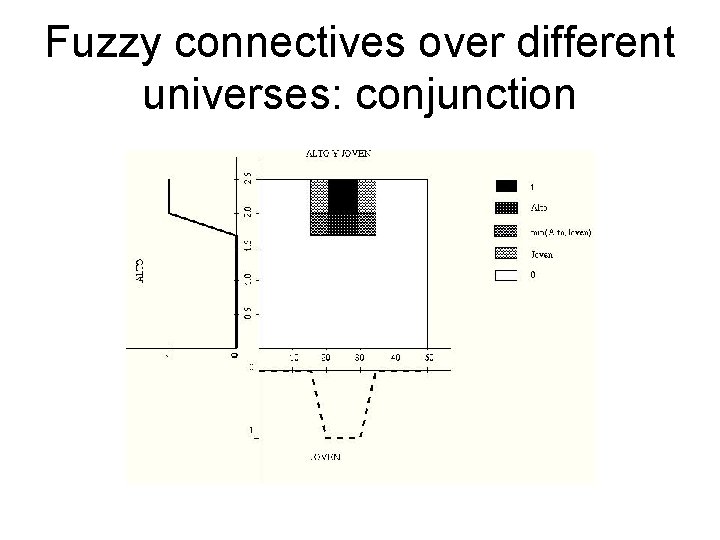
Fuzzy connectives over different universes: conjunction

Fuzzy connectives over different universes: conjunction

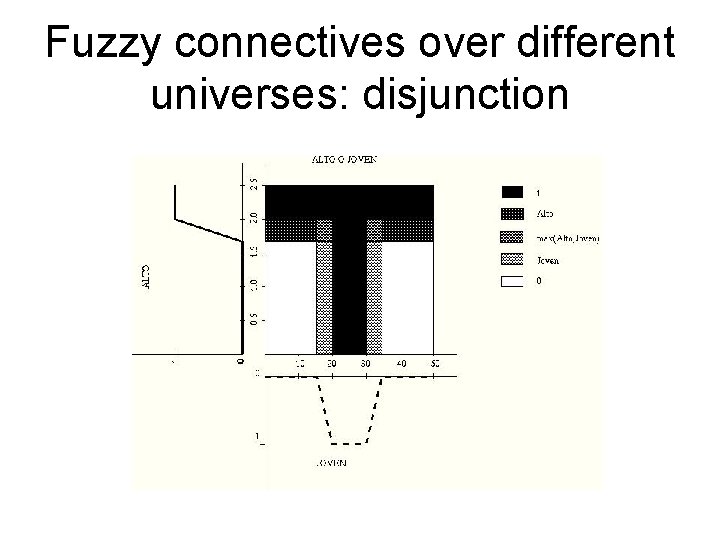
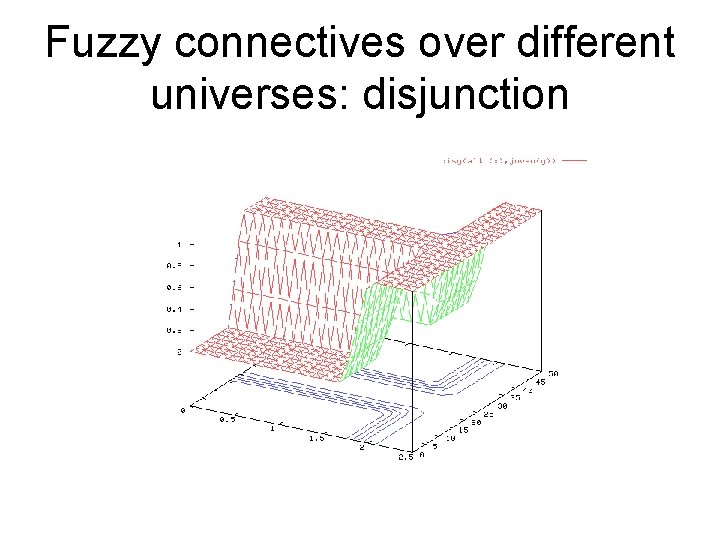
Fuzzy connectives over different universes: disjunction

Fuzzy connectives over different universes: disjunction

Fuzzy inference with crisp data • Rule base where atoms are fuzzy labels [X = A]: R 1: If R 2: If R 3: If R 4: If T = MC and ΔT = PM then VC = PN T = MC and ΔT = PP then VC = PN T = A and ΔT = PP then VC = GZ • How to combine these rules for inference? Temperature • [Gelada] • [Molt Freda] • [Fresca] • [Agradable] • [Calenta] • [Molt Calenta]

Fuzzy inference with crisp data: connectives • Interpretation of connectives: – Negation: N(x) = 1 -x – Conjunction: fuzzy intersection = T-norms (T) – Disjunction: fuzzy union = T-conorms (S) 27

Fuzzy inference with crisp data: phases 1. Evaluation of the antecedent of the rules 2. Evaluation of the conclusions of the rules 3. Combination of the conclusions of the rules 4. Defuzzification

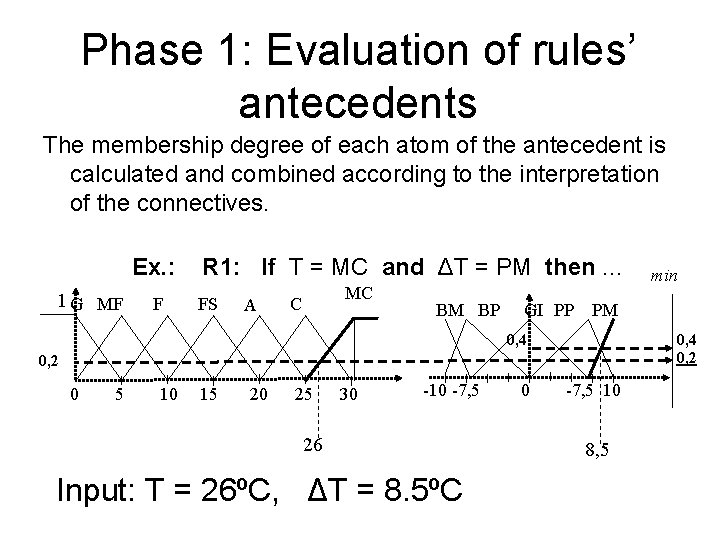
Phase 1: Evaluation of rules’ antecedents The membership degree of each atom of the antecedent is calculated and combined according to the interpretation of the connectives. Ex. : 1 G MF F R 1: If T = MC and ΔT = PM then. . . FS A MC C BM BP GI PP PM 0, 4 0, 2 0 5 10 15 20 25 30 -10 -7, 5 26 Input: T = 26ºC, ΔT = 8. 5ºC min 0 -7, 5 10 8, 5

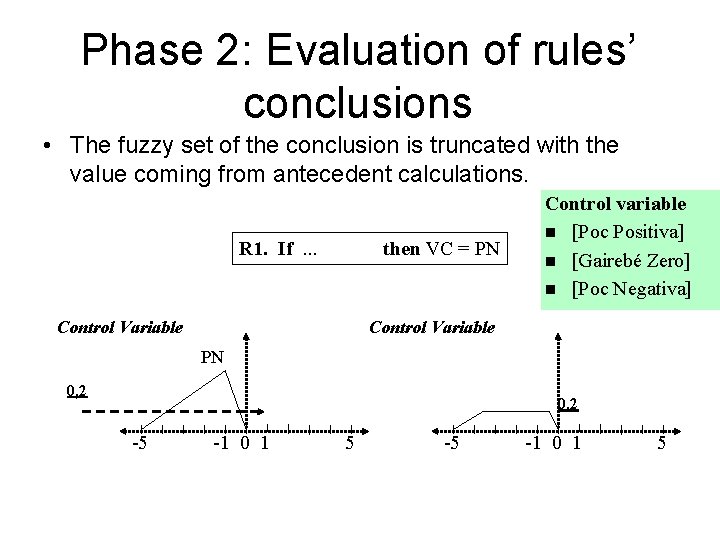
Phase 2: Evaluation of rules’ conclusions • The fuzzy set of the conclusion is truncated with the value coming from antecedent calculations. R 1. If. . . then VC = PN Control Variable Control variable n [Poc Positiva] n [Gairebé Zero] n [Poc Negativa] Control Variable PN 0, 2 -5 -1 0 1 5

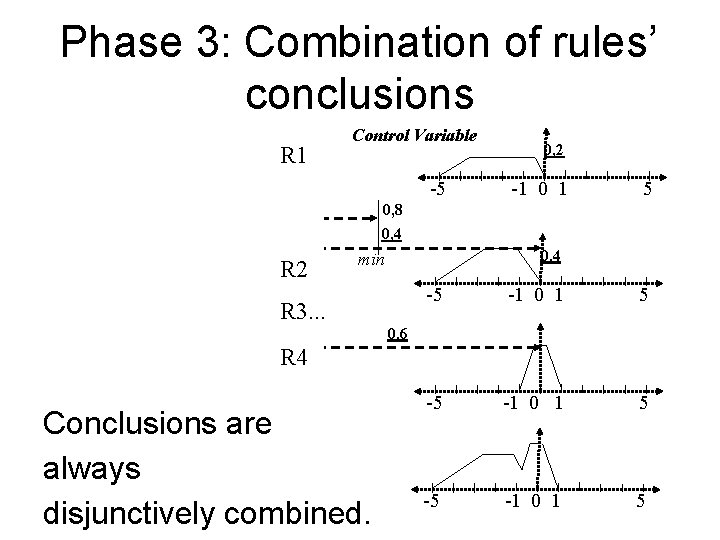
Phase 3: Combination of rules’ conclusions R 1 Control Variable -5 0, 2 -1 0 1 5 0, 8 0, 4 R 2 0, 4 min R 3. . . -5 -1 0 1 5 0, 6 R 4 Conclusions are always disjunctively combined.

Phase 4: defuzzification • Defuzzification Σ x∈D μ(x) · x Σ x∈D μ(x) mass center -5 -1 0 1 5 -5 – 1. 5 0 1 5

33

Inferència difusa amb dades difuses Tenim una base de regles on els àtoms son etiquetes difuses [X = A] Si Temperatura = Agradable … llavors Gir = Una mica a la dreta • Volem fer inferència: – amb encadenament cap endavant; – a partir d’etiquetes difuses per les variables.

Inferència difusa amb dades difuses: Fases 1. Avaluació de la relació expressada en cada regla (grau o funció d’implicació) μI(x, y) 2. Avaluació de la funció de pertinença de l’antecedent μA(x) 3. Composició inferencial (Modus ponens) de la implicació i l’antecedent μCI(x, y) = f(μI(x, y), μA(x))

Inferència difusa amb dades difuses: Implicació Funcions d’implicació, I : [0, 1] x [0, 1] → [0, 1] • Propietats • I(p, q) és creixent respecte a la primera variable i decreixent respecte a la segona variable • I(0, p) = 1 • I(1, p) = p • I(p, I(q, r)) = I(q, I(p, r)) (intercanvi d’antecedents) • R-implicacions / S-implicacions • a → b = ¬ a ∨ b • I(x, y) = S(N(x), y) • Exemples de S-implicacions • I(x, y) = màx (1 -x, y) • I(x, y) = 1 -x+x*y • I(x, y) = mín (1 -x+y, 1)

Inferència difusa amb dades difuses: Modus ponens Les inferències en lògica difusa utilitzen el modus ponens com a regla bàsica: Si [X és A] llavors [Y és B ] [X és A] [Y és B ] La combinació de funcions de possibilitat es realitza mitjançant la funció generadora de modus ponens.

Modus ponens Emprant algunes de les definicions anteriors d’implicació i el modus ponens, és possible definir el procés d’inferència difusa: p ∧ (p → q) → q Donades les certeses d’un antecedent i de la implicació, la determinació de la certesa del conseqüent es realitza en base a una funció generadora del modus ponens que denominem mod(). La funció mod() té una sèrie de propietats, algunes de les quals són les següents: b) a) Aquest La funció és mod() el límitté booleà com adel a) mod(u, imp(u, v)) ≤ v c) antecedent completament d) D’un La funció mod() ha de ser modus cota superior ponens la certesa del fals es pot concloure qualsevol monòtona creixent amb la certesa b) mod(1, 1) = 1 conseqüent. cosa. de l’antecedent. c) mod(0, u) = v d) u ≤ v ⇒ mod(u, w) ≤ mod(v, w)

Modus ponens Funciones generadoras del modus ponens que resultan de las definiciones de la función implicación presentadas anteriormente:

Generalització del modus ponens La lògica difusa gaudeix de l’avantatge de poder fer inferències sense tenir exactament l’antecedent d’una regla: Si [X és A] llavors [Y és B] [X és A’] [Y és B’ ] S’ha de calcular com es modifica la conclusió, ja que no tenim el mateix antecedent de la regla. Això es fa mitjançant la transformació de la funció de possibilitat de A’ en la de A