Artificial Intelligence CS 370 D Prolog programming Syntax

Artificial Intelligence CS 370 D Prolog programming Syntax and meaning of prolog programs 1

Outline: n Data Objects. n Lexical Scope. n Structured Objects. n Examples of Structured Objects. n Matching. n Examples of matching. 2

Data Objects: n In Previous lab: n n Variables start with upper-case letters Atoms start with lower-case letters data objects simple objects constants atoms numbers structures variables 3

Lexical Scope: n The lexical scope of variable names is one clause. n If the name X occurs in two clauses, then it signifies two different variables. hasachild(X) : - parent( X, Y). isapoint(X) : - point( X, Y, Z). n But each occurrence of X with in the same clause means the same variables. hasachild( X) : - parent( X, Y). n The same atom always means the same object in any clause throughout the whole program. 4

Structured Objects: n Structured objects are objects that have several components. n All structured objects can be pictured as trees. n The root of the tree is the functor. n The offsprings of the root are the components. n Components can also be variables or atoms. date( Day, September, 2015) n Example: date( 18, September, 2015) date 18 (functor, root) September 2015 (arguments) n All data objects in Prolog are terms. 5

Structured Objects (cont): n Each functor is defined by two things: n The name, whose syntax of atoms; n The arity—that is, the number of arguments. n For example: point( X 1, Y 1) and point( X, Y, Z) are different. The Prolog system will recognize the difference by the number of arguments, and will interpret this name as two functors. 6

Examples of Structured Objects: n The tree structure corresponding to the arithmetic expression (a + b)*(c - 5). n Using the simples ‘*’, ’+’ and ‘-’ as functors n In fact, Prolog also allows us to use the infix notation. *(+( a, b), -( c, 5)) ? - X = *(+( a, b), -( c, 5)). ? - X is *(+( 3, 4), -( 6, 5)). * ＋ * － ＋ － 7 a b c 5 3 4 6 5

Examples of Structured Objecs: n Choose the following functors: point for points, seg for line segments, and triangle for triangles. n Representation: P 1 = point( 1, 1) P 2=(2, 3) S (4, 2) P 1=(1, 1) (6, 4) T (7, 1) P 2 = point( 2, 3) S = seg( P 1, P 2) = seg( point(1, 1), point(2, 3)) 8 T = triangle( point(4, 2), point(6, 4), point(7, 1))

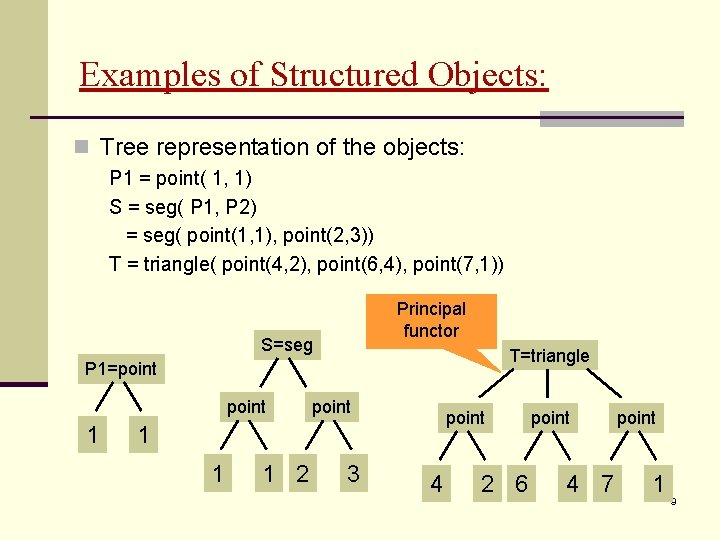
Examples of Structured Objects: n Tree representation of the objects: P 1 = point( 1, 1) S = seg( P 1, P 2) = seg( point(1, 1), point(2, 3)) T = triangle( point(4, 2), point(6, 4), point(7, 1)) Principal functor S=seg T=triangle P 1=point 1 1 1 2 3 4 2 6 point 4 7 point 1 9

Matching: n The most important operation on terms is matching. n Matching is a process that takes as input two terms and checks whether they match. n n Fails: if the terms do not match Succeeds: if the terms do match n Given two terms, we say that they match if: n n n they are identical , or the variable in both terms can be instantiated to objects in such a way that after the substitution of variables by these objects the terms become identical. For example: n n the terms date( D, M, 2001) and date( D 1, may, Y 1) match the terms date( D, M, 2001) and date( D 1, M 1, 1444) do not match 10

Examples of matching: n The request for matching, using the operator ‘=‘: Examples: ? - date( D, M, 2001) = date(D 1, may, Y 1). D = D 1, M = may, Y 1 = 2001. ? - date( D, M, 2015) = date(D 1, may, Y 1), date( D, M, 2015) = date( 15, M, Y). D = D 1, D 1 = 15, M = may, Y 1 = Y, Y = 2015. 11

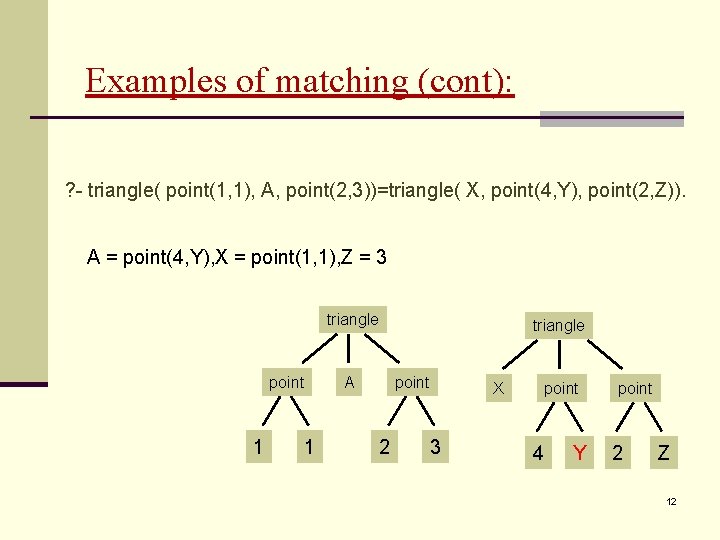
Examples of matching (cont): ? - triangle( point(1, 1), A, point(2, 3))=triangle( X, point(4, Y), point(2, Z)). A = point(4, Y), X = point(1, 1), Z = 3 triangle point 1 A 1 triangle point 2 X 3 point 4 Y point 2 Z 12

Examples of matching (cont): An example: point(1, 1). ? - vertical( seg( point(1, 1), point(1, 2). 1, 2))). point(2, 4). true seg(point(1, 1), point(1, 2)). seg(point(1, 1), point(2, 4)). seg(point(1, 2), point(2, 4)). vertical( seg( point( X, Y), point( X, Y 1))). horizontal( seg( point( X, Y), point( X 1, Y))). ? - vertical( seg( point(1, Y), point(2, Y))). false ? - horizontal( seg( point(1, 1), point(2, Y))). Y=1 13

Examples of matching (cont): ? - horizontal( seg( point(1, 1), P)). P = point(_, 1) P = point(_G 1088, 1). * ? - vertical( seg( point(1, 1), P)). P = point(1, _) P = point(1, _G 1077). * The answer means: Yes, any segment that ends at any point (1, _), which means anywhere on the vertical line x =1. ? - vertical( S), horizontal( S). S = seg( point( A, B), point( A, B)) S = seg(point(_G 1097, _G 1098), point(_G 1097, _G 1098)). * The answer means: Yes, any segment that is degenerated to a point has the property of being vertical and horizontal at the same time. 14