Artificial Intelligence 7 Making Deductive Inferences Course V

Artificial Intelligence 7. Making Deductive Inferences Course V 231 Department of Computing Imperial College, London Jeremy Gow

Automating Deductive Reasoning l Aims of automated deduction – – l Theorem proving – – l Deduce new knowledge from old Prove/disprove some open conjectures Search for a path from axioms to theorem statement Operators are (sound) inference rules Applications: – – Agents that use deductive inference Mechanising and automating mathematics Verifying hardware and software specifications The semantic web

Inference Rules l A entails B iff – – l l B is true when A is true Any model of A is a model of B Then this is a sound inference rule A B Axioms C D … Z Theorem – – Each step is application of inference rule Theorem is entailed by the axioms

Tautologies • S: (X (Y Z)) ((X Y) (X Z)) • Show that no matter what truth values for X, Y and Z • • The statement S is always true X Y Z X Y X Z X (Y Z) ((X Y) (X Z)) S true true true false false true false true false false true true true false true true false true true false true true Columns 7 and 8 are always the same

Inference with Tautologies l P Q Q P is obviously true – – l Regardless of meaning or truth values of P and Q This is content-free and a tautology One way to define a rule of inference: – – – We can replace P Q with Q P, and vice versa They are true for same models Replacing one for other preserves soundness

Equivalence Rules l A and B are logically equivalent (write A B) – – l Formalised as rewrite rule A B – – – l Same models for each Can replace any instance of A with an instance of B without affecting models Also B A Must avoid looping A B . . . Choose one direction, or always loop-check Rewrite rules used for inference – – Showing theorem and axioms are equivalent Preprocessing theorem/axioms into a particular format

Commutativity & Associativity l Commutativity P Q P Q l Q P P (Q R) Q P Associativity (P Q) R P (Q R)

Distributivity of Connectives l ‘and over or’ and ‘or over and’: P (Q R) l (P Q) (P R) Over implication P (Q R) (P Q) (P R)

Double Negation l Have to be careful in English – – l “I’m not hungry” Does not (necessarily) mean: “I’m hungry” But double negations can always be removed ¬¬P l P Humans would not write this – But it may appear in during agent’s inference

De Morgan’s Law & Contraposition l De Morgan’s Law (refers to either) ¬(P Q) l ¬P ¬Q Contraposition: imagine the opposite is true – P Q ¬P Often useful in mathematics proof

Other Equivalences l l Remove implication or equivalence (very useful) – P Q ¬P Q (P Q) (Q P) Reduce to truth value P ¬P False True

An Example Deduction (P Q) (¬P Q) l Show that this sentence is false – – l l Show that this rewrites to False This proves the negation See notes for solution (or do as exercise) Is this easier than a truth table?

Propositional Inference Rules l Rewrite rules are good for bidirectional search – l Classic example – – l All men are mortal, socrates is a man Therefore: Socrates is mortal This is an instance of an inference rule – l But we don’t need equivalence, just entailment Known as Modus Ponens (Aristotle) A B, A B Above line: what we know, below: what we can deduce

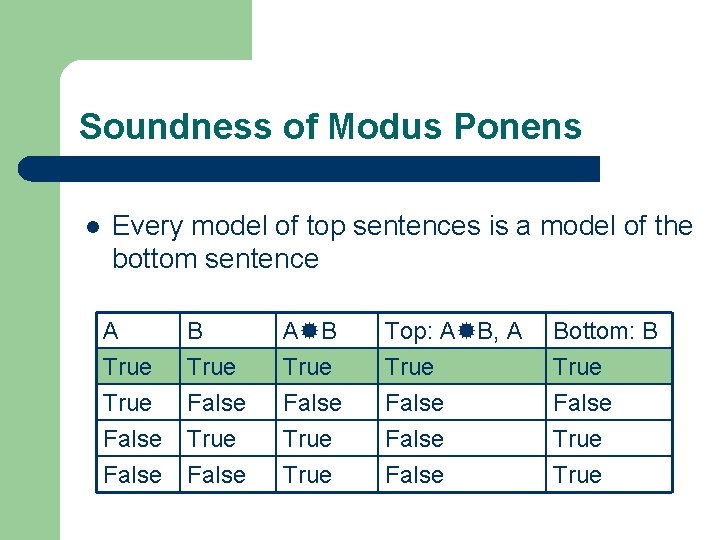
Soundness of Modus Ponens l Every model of top sentences is a model of the bottom sentence A True False B True False True A B Top: A B, A True False Bottom: B True False True

And-Elimination & -Introduction l And-Elimination: A 1 A 2 … A n Ai [1 i n] l And-Introduction: A 1, A 2, …, An A 1 A 2 … A n l The sentences may be from different places – Selected from the database

Or-Introduction & Unit Resolution l Or-introduction Ai A 1 A 2 … A n [1 i n] l Unit resolution (A B) , ¬B A l Basis for resolution theorem proving – See next two lectures

First-Order Inference Rules l Propositional inference rules (inc. equivs) – l l First-order inference more complicated Soundness depends on concept of models – l Can all be used in first-order inference Potentially infinite models, can’t use a truth table Sentences contain quantifiers – Need the notion of ground substitution

Substitution & Instantiation l FOL sentences have quantified variables – – l Instantiation (grounding) is a kind of substitution – l l Substitute into a variable by assigning a particular value Replace with given term, remove quantifier Must substitute a ground term Example: X. Y. likes(X, Y) becomes likes(tony, george) We write: – Subst({X/tony, Y/george}, likes(X, Y)) = likes(tony, george)

Universal Elimination l Given a sentence, A – – Containing a universally quantified variable V Then we can replace V by any ground term g V. A Subst({V/g}, A) l l Remember to remove quantifier Not as complicated as it looks: X likes(X, ice_cream) becomes likes(ben, ice_cream)

Existential Elimination l Given a sentence, A – – – Containing an existentially quantified variable, V Then we can replace V by any constant, k As long as k is not mentioned anywhere else V. A Subst({V/k}, A) l For the sake of argument, let’s call it…

Existential Introduction l Given a sentence, A – – And a variable, V, which is not used in A Then any ground term, g, in A can be substituted by V l As long as g does not appear in A also A V. Subst({g/V}, A) l Exercise: find sentence where V is in A – Such that this inference rule is not sound

Chains of Inference l Remember the problem we’re trying to solve – l Three approaches – – – l Search for a path from axioms, A, to theorem, T Forward chaining Backward chaining Proof by contradiction Specification of a search problem: – – Representation of states (first-order logic sentences) Initial state (depends. . . ) Operators (inference rules, including equivalences) Goal state (depends. . . )

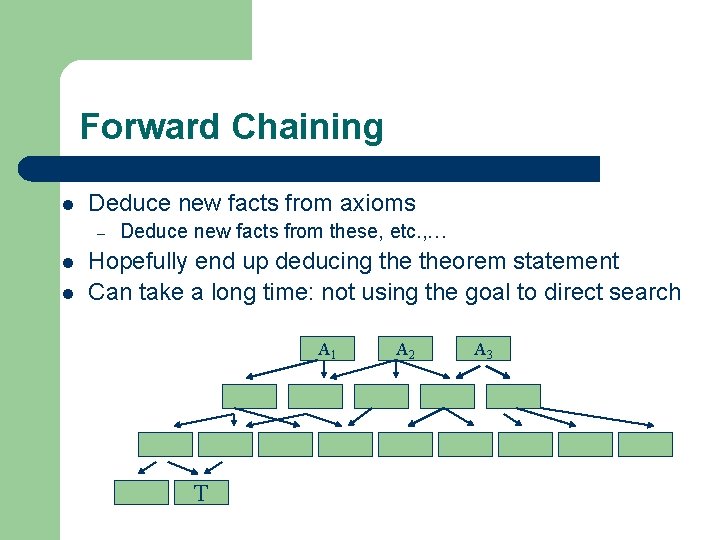
Forward Chaining l Deduce new facts from axioms – l l Deduce new facts from these, etc. , … Hopefully end up deducing theorem statement Can take a long time: not using the goal to direct search A 1 T A 2 A 3

Backward Chaining l Start with theorem state and work backwards – l Each step asks: given the state that I’m at. . . – l Which operator could have been applied to which state to produce the state (sentence) I’m at No problem when using equivalences – l Hope to end up at the axioms Can also use a bidirectional search (from both ends) Difficult when using general inference rules – Many possible ways to invert operators

Proof By Contradiction l l “Reductio ad absurdum” Assume theorem is false – – l Add negated theorem to the set of axioms – l then show that the assumption contradicts the axioms which proves that theorem is true See if we can deduce the ‘False’ sentence Advantage: using theorem statement from start – Can look to see how close we are to the false statement l l Possibilities for a heuristic search! Basis for resolution theorem proving

Example: using the Otter resolution theorem prover Input to Otter: set(auto). formula_list(usable). all x (man(x)->mortal(x)). % For all x, if x is a man then x is mortal man(socrates). % Socrates is a man -mortal(socrates). % Socrates is immortal (note: negated) end_of_list. Output from Otter: -------- PROOF --------1 [] -man(x)|mortal(x). 2 [] -mortal(socrates). 3 [] man(socrates). 4 [hyper, 3, 1] mortal(socrates). 5 [binary, 4. 1, 2. 1] $F. ------ end of proof -------