Articulated Bodies Tracking Eran Sela Articulated Body Every

Articulated Bodies Tracking Eran Sela
Articulated Body • Every general 3 D motion can be perceived by a moving group of joints and links. • An articulated body has only joints and fixed length limbs.
Motivation • Based on input data such as depth map, color, silhouette map – We’ll see today two works about: • How to implement realtime skeleton tracking on the articulated body. • The tracking can be used to move computers graphic models & to capture 3 D motion of human’s body.

Tracking Methods �Supervised or semi-supervised learning trackers: Training sorts of decision trees or other statistical models based on labeled & unlabeled data. �Model based skeleton tracking: Modeling the human body with primitives/surfaces and fitting the model to the data using an optimization scheme. �Image processing based tracking: Generate skeleton based on mathematical condition the data conform to.

Presentation timeline 1. Articulated Soft Objects for Video-based Body Modeling �Modeling the articulated body �Optimization framework to the data (Least squares). �Data constraints �Results 2. A Multiple Hypothesis Approach to Figure Tracking �Introduction �The 2 D Scaled Prismatic Model �Mode-based Multiple-Hypothesis Tracking �Multiple Modes as Piecewise Gaussians �Results

Articulated Soft Objects for Video-based Body Modeling Input: Video sequence containing: �Depth map (using stereo cameras or other method). �Silhouette map (The points where the line of sight from the camera is tangent to the surface). Output: �A set of 3 D ellipsoid primitives with translation, orientation and scale corresponding to the articulated body parts.

Modelling with Primitives vs Soft objects Problem: primitive models such as cylinder and spheres are too crude for precise recovery of both shape and motion Solution: use Soft objects. Each primitive defines a field function and the skin is taken to be a level set of the sum of these fields. Has the following advantages: • Effective use of stereo and silhouette data • Accurate shape description by a small number of parameters. • Explicit modeling of 3–D geometry

Modelling with Primitives vs Soft objects Problem: primitive models such as cylinder and spheres are too crude for precise recovery of both shape and motion Solution: use Soft objects. Each primitive defines a field function and the skin is taken to be a level set of the sum of these fields. Has the following advantages: • Effective use of stereo and silhouette data • Accurate shape description by a small number of parameters. • Explicit modeling of 3–D geometry

Modelling with Primitives vs Soft objects Problem: primitive models such as cylinder and spheres are too crude for precise recovery of both shape and motion Solution: use Soft objects. Each primitive defines a field function and the skin is taken to be a level set of the sum of these fields. Has the following advantages: • Effective use of stereo and silhouette data • Accurate shape description by a small number of parameters. • Explicit modeling of 3–D geometry

Modelling the body parts: State Vector: B – number of body parts N – number of consecutive frames J – number of joints The state vector θ changes on each frame.

Generalized algebraic surfaces �

Generalized algebraic surfaces �
![Metaballs Blinn [2] Metaballs (Generalized algebraic surfaces), are defined by a summation over n Metaballs Blinn [2] Metaballs (Generalized algebraic surfaces), are defined by a summation over n](http://slidetodoc.com/presentation_image_h/87f4b06b6ee97440cb6691624f321ad5/image-13.jpg)
Metaballs Blinn [2] Metaballs (Generalized algebraic surfaces), are defined by a summation over n 3 -dimensional Gaussian density distributions, each called a source or primitive. The final surface S is found where the density function F equals some threshold amount, in our case:

Ellipsoids as sources Why choosing ellipsoids as sources for metaballs? �They are simple �Allow accurate modeling of human limbs with relatively few primitives �Their shape is controlled by higher level width and length parameters And thus problems like over-fitting to high-curvature regions do not occur. Next we define the 3 D quadratic distance Function d() from the (x, y, z) point to each ellipsoid source.

3 D Quadratic distance For a specific metaball and a state vector θ we define 4 x 4 matrix: Is the scaling and translation along the major axis of the ellipsoid is the radii of the ellipsoid (half the axis length along the principal directions. is the primitive’s center. are the coefficients from the state vector.

3 D Quadratic distance
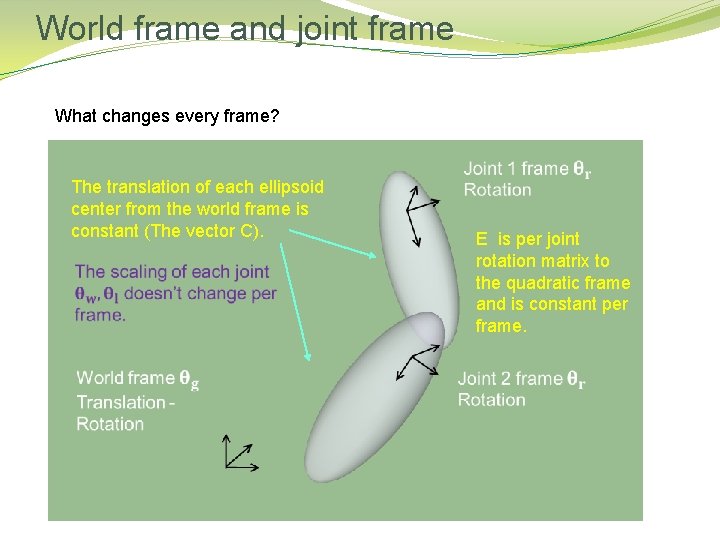
World frame and joint frame What changes every frame? The translation of each ellipsoid center from the world frame is constant (The vector C). E is per joint rotation matrix to the quadratic frame and is constant per frame.

3 D Quadratic distance is the skeleton induced transformation. A 4 x 4 rotation-translation matrix From the world frame to the frame to which the metaball is attached. Given the rotation of a joint J, we write: Is homogenous 4 x 4 transformation from the joint frame to the quadric frame. Is transformation from the world frame to joint frame. Is the ellipsoidal quadratic distance field.

Least Square Framework

Least Square Framework Least squares optimization framework is used to estimate the state vector parameters:

Least Square Framework Solution to the optimization problem is based on Levenberg-Marquardt algorithm For solving the least squares problem, and find the new state vector θ. The Jacobian matrix is calculated for any point x:
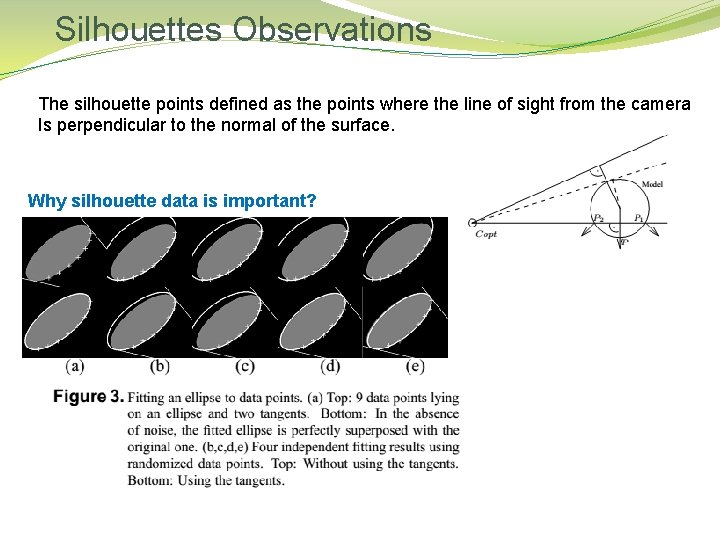
Silhouettes Observations The silhouette points defined as the points where the line of sight from the camera Is perpendicular to the normal of the surface. Why silhouette data is important?

Integrate silhouette constraint

Integrate silhouette constraint • We integrate silhouette observations into our framework by performing an initial search (using Brent’s line minimization) along the line of sight to find the point that is closest to the model at its current configuration. • Then we find the closest silhouette point to the model we give it a higher weight in the P weight matrix, so the silhouette points are more significant for the fitting.

Fitting Result Sensor configuration: • Depth is acquired by 3 cameras in an L configuration taking non-interlaced images at 30 frames/sec, with an effective resolution of 640 x 400. • stereo algorithm produced very dense point clouds which are then filtered yielding about 4000 evenly distributed 3–D points on the surface of the subject • In the top row are the original sequences of upper body motions of different persons. Results of the tracking and fitting are shown in the bottom row. Although the two persons have very different body sizes the system adjusts the generic model accordingly.

Fitting Result First person: Second person:

End of topic 1

Presentation timeline 1. Articulated Soft Objects for Video-based Body Modeling �Modeling the articulated body �Optimization framework to the data (Least squares). �Data constraints �Results 2. A Multiple Hypothesis Approach to Figure Tracking �Introduction �The 2 D Scaled Prismatic Model �Mode-based Multiple-Hypothesis Tracking �Multiple Modes as Piecewise Gaussians �Results
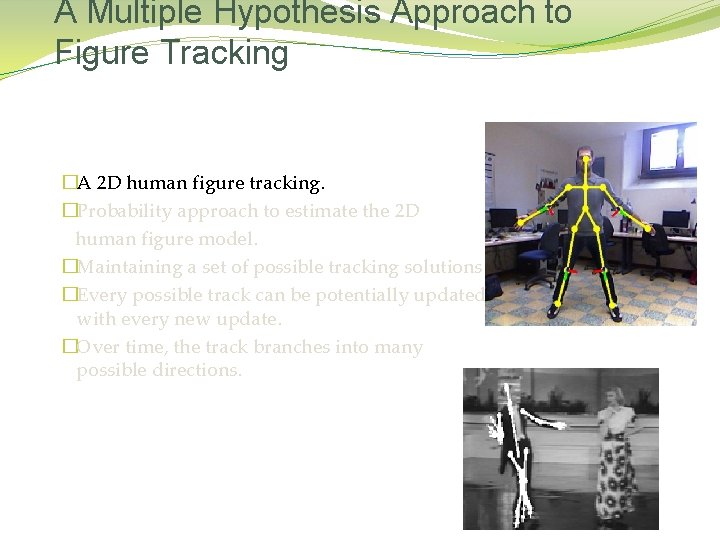
A Multiple Hypothesis Approach to Figure Tracking �A 2 D human figure tracking. �Probability approach to estimate the 2 D human figure model. �Maintaining a set of possible tracking solutions. �Every possible track can be potentially updated with every new update. �Over time, the track branches into many possible directions.
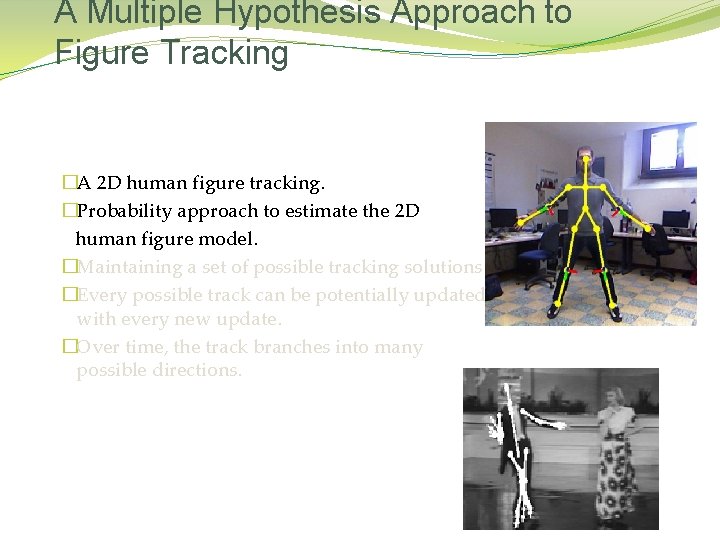
A Multiple Hypothesis Approach to Figure Tracking �A 2 D human figure tracking. �Probability approach to estimate the 2 D human figure model. �Maintaining a set of possible tracking solutions. �Every possible track can be potentially updated with every new update. �Over time, the track branches into many possible directions.
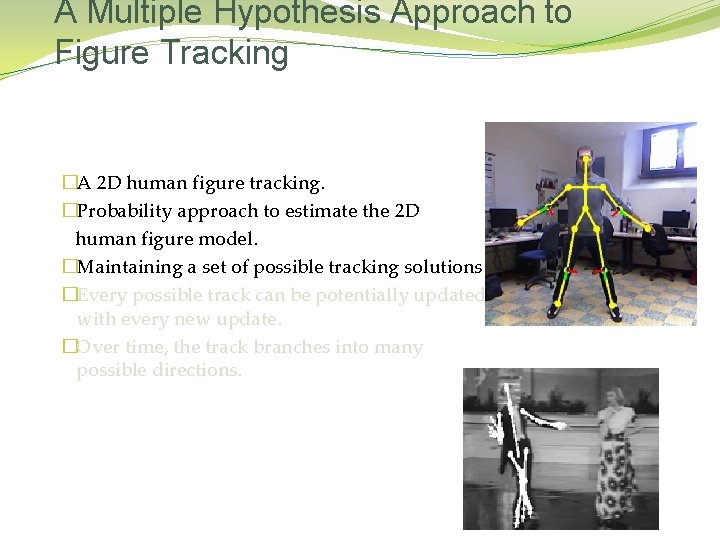
A Multiple Hypothesis Approach to Figure Tracking �A 2 D human figure tracking. �Probability approach to estimate the 2 D human figure model. �Maintaining a set of possible tracking solutions. �Every possible track can be potentially updated with every new update. �Over time, the track branches into many possible directions.
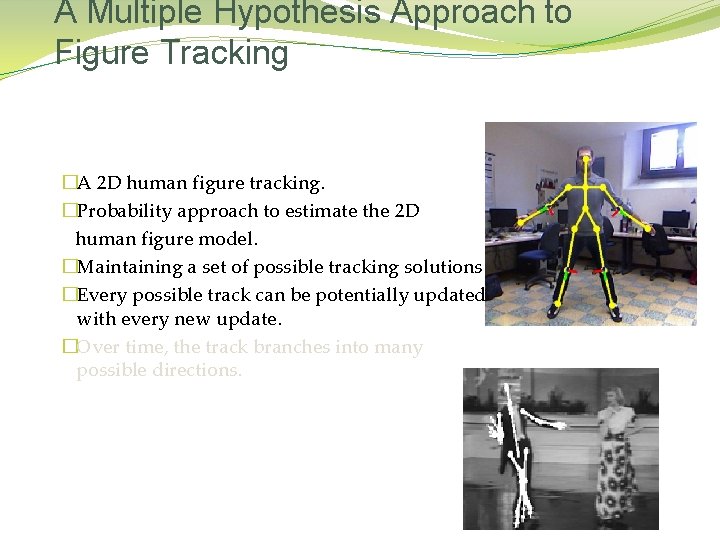
A Multiple Hypothesis Approach to Figure Tracking �A 2 D human figure tracking. �Probability approach to estimate the 2 D human figure model. �Maintaining a set of possible tracking solutions. �Every possible track can be potentially updated with every new update. �Over time, the track branches into many possible directions.

A Multiple Hypothesis Approach to Figure Tracking �A 2 D human figure tracking. �Probability approach to estimate the 2 D human figure model. �Maintaining a set of possible tracking solutions. �Every possible track can be potentially updated with every new update. �Over time, the track branches into many possible directions.

Used in radars • The MHT is designed for situations in which the target motion model is very unpredictable, as all potential track updates are considered. • As each radar update is received every possible track can be potentially updated with every new update. Over time, the track branches into many possible directions.

The 2 D Scaled Prismatic Model How we can enforce 3 D kinematic constraints of the model that conform to the 2 D monocular image data? Scaled Prismatic Models (SPM): • Each link in a scaled prismatic model describes the image plane projection of an associated rigid link in an underlying 3 D kinematic chain. • Each link has 2 DOF: the distance between the joint centers of adjacent links, and the rotation angle at its joint center around an axis which is perpendicular to the image plane. • It captures the foreshortening that occurs when 3 D links rotate into and out of the image plane.

The 2 D Scaled Prismatic Model How we can enforce 3 D kinematic constraints of the model that conform to the 2 D monocular image data? Scaled Prismatic Models (SPM): • Each link in a scaled prismatic model describes the image plane projection of an associated rigid link in an underlying 3 D kinematic chain. • Each link has 2 DOF: the distance between the joint centers of adjacent links, and the rotation angle at its joint center around an axis which is perpendicular to the image plane. • It captures the foreshortening that occurs when 3 D links rotate into and out of the image plane.

The 2 D Scaled Prismatic Model How we can enforce 3 D kinematic constraints of the model that conform to the 2 D monocular image data? Scaled Prismatic Models (SPM): • Each link in a scaled prismatic model describes the image plane projection of an associated rigid link in an underlying 3 D kinematic chain. • Each link has 2 DOF: the distance between the joint centers of adjacent links, and the rotation angle at its joint center around an axis which is perpendicular to the image plane. • It captures the foreshortening that occurs when 3 D links rotate into and out of the image plane.

Tracking problem representation �We model the human 2 D figure as a branched SPM chain. �Each link in the arms, legs, and head is modeled as an SPM link. �Each link 2 DOF, leading to a total body model with 18 DOF’s. �The tracking problem consists of estimating a vector of SPM parameters for the figure in each frame of a video sequence, given some initial state.

Probability Density Representation �The choice of representation for the probability density of a tracker state is largely dominated by two concerns: � The unimodality constraint imposed when using a Gaussian-based parametric representation such as the Kalman Filter is inaccurate when tracking in a cluttered environment. �Sample-based representation (such as used in the CONDENSATION algorithm) requires a prohibitive number of samples for encoding the probability distribution of a high-DOF SPM model.

Condensation Algorithm �Condensation algorithm is an application of particle filtering in which: �Observations and hidden states are represented by hand contours. �Contours can be represented as splines, list of angles between phalanxes, etc. �There is a model for P(next state|previous state). �Can be set manually by studying the anatomy of a hand. �Can be learned by gathering lots of examples of sequences of hand movement. �Learning can be done using special gloves which report exact hand location and shape. �P(state|observation) is estimated using visual features (SIFT, Harris, etc. )

Probability Density Representation A hybrid approach: �Supports a multimodal description but requires fewer samples for modeling. �The representation is based on retaining only the modes (or peaks) of the probability density and modeling the local neighborhood surrounding each mode with a Gaussian.

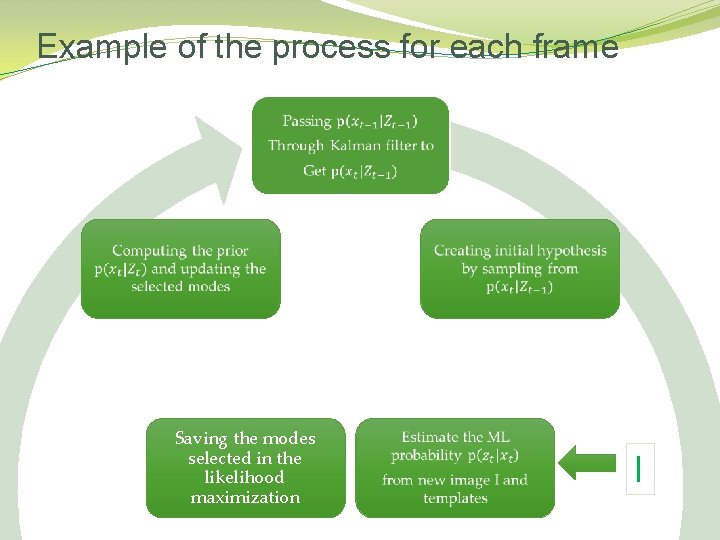
MHT Algorithm � Input: �Video sequence containing 1 or more humans � Output: � A state vector per each frame of values for all the DOF of the SPM chains assembling the model.

Mode-based Multiple-Hypothesis Tracking (Bayes rule)

The algorithm �

The algorithm �

The algorithm �

The algorithm �

The algorithm �

Generating Prior Distributions � Kalman Filter

Kalman Filter State Prediction: Measurement Prediction:

Kalman Filter • Two groups of the equations for the Kalman filter: o Time update equations (Prediction) o Measurement update equations. (Correction) • The time update equations are responsible for projecting forward (in time) the current state and error covariance estimates to obtain the a priori estimates for the next time step. • The measurement update equations are responsible for the feedback—i. e. for incorporating a new measurement into the a priori estimate to obtain an improved a posteriori estimate.

Kalman Filter Update Predict 1. Predict the state ahead: 2. Predict the error covariance ahead: 1. Update the state estimate: 2. Update the error covariance: where Kalman gain Kt is: 52

Multiple Modes as Piecewise Gaussians �

Multiple Modes as Piecewise Gaussians �

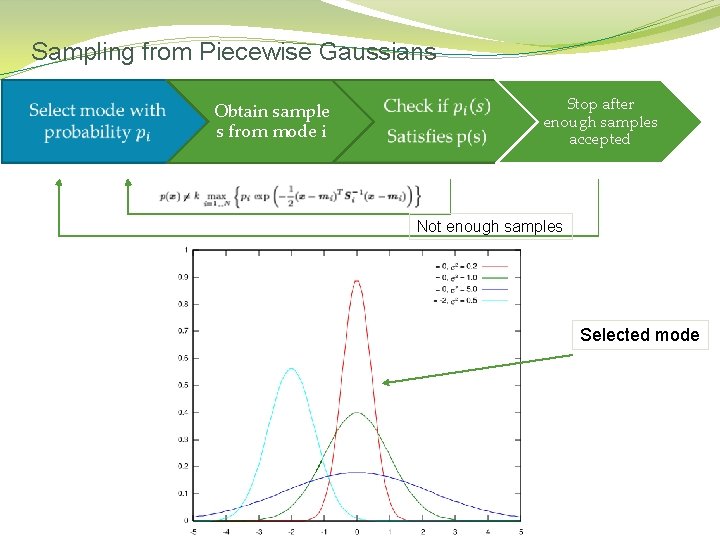
Sampling from Piecewise Gaussians �
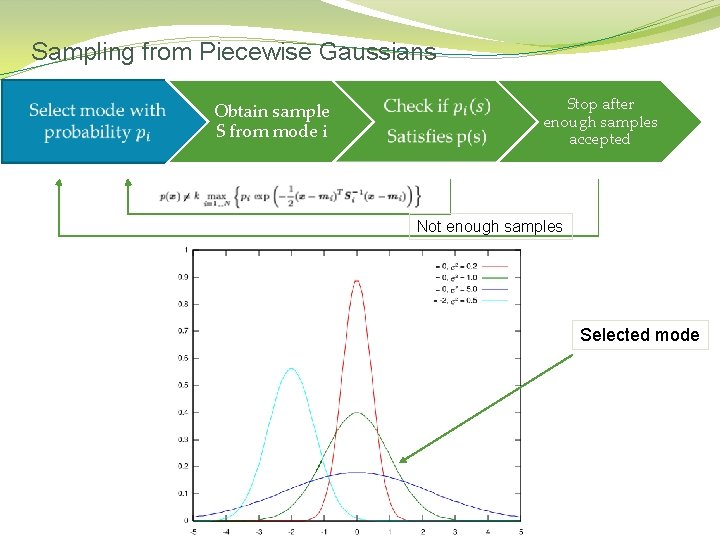
Sampling from Piecewise Gaussians Obtain sample S from mode i Stop after enough samples accepted Not enough samples Selected mode
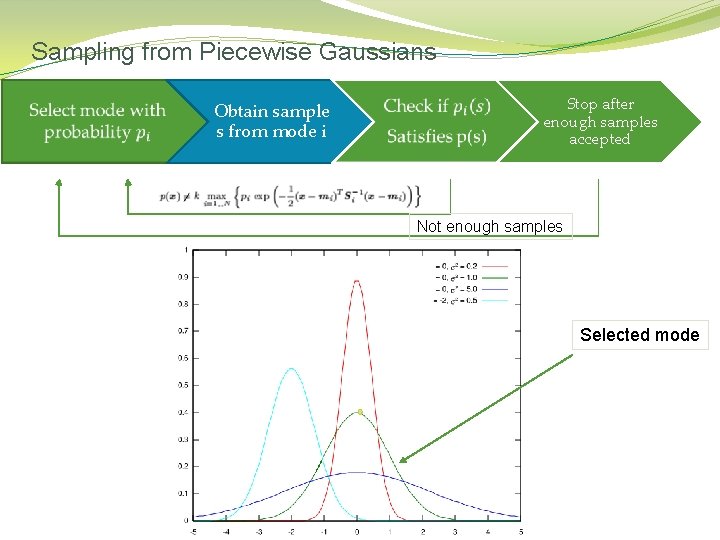
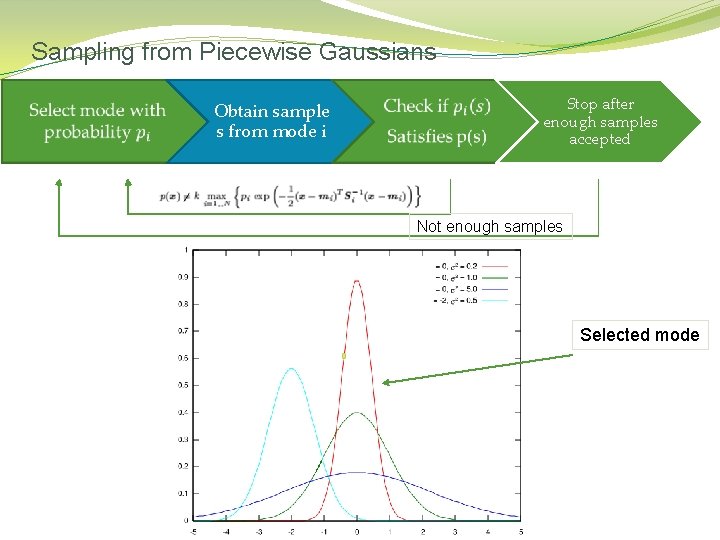
Sampling from Piecewise Gaussians Obtain sample s from mode i Stop after enough samples accepted Not enough samples Selected mode
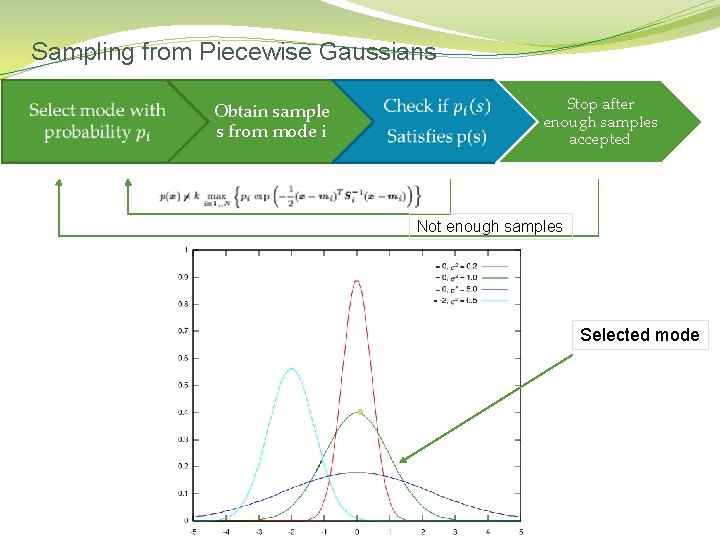
Sampling from Piecewise Gaussians Obtain sample s from mode i Stop after enough samples accepted Not enough samples Selected mode
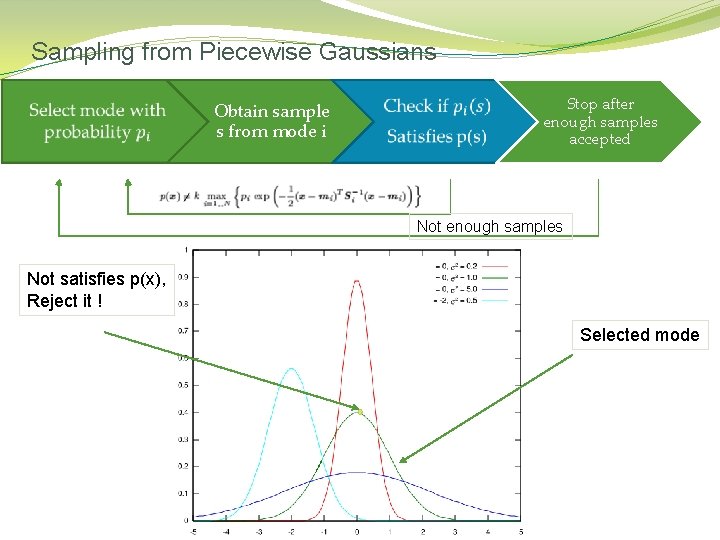
Sampling from Piecewise Gaussians Obtain sample s from mode i Stop after enough samples accepted Not enough samples Not satisfies p(x), Reject it ! Selected mode
Sampling from Piecewise Gaussians Obtain sample s from mode i Stop after enough samples accepted Not enough samples Selected mode
Sampling from Piecewise Gaussians Obtain sample s from mode i Stop after enough samples accepted Not enough samples Selected mode
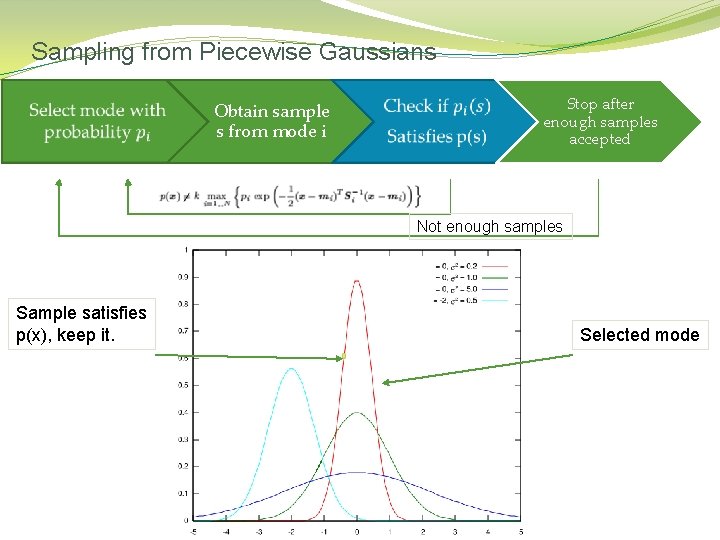
Sampling from Piecewise Gaussians Obtain sample s from mode i Stop after enough samples accepted Not enough samples Sample satisfies p(x), keep it. Selected mode
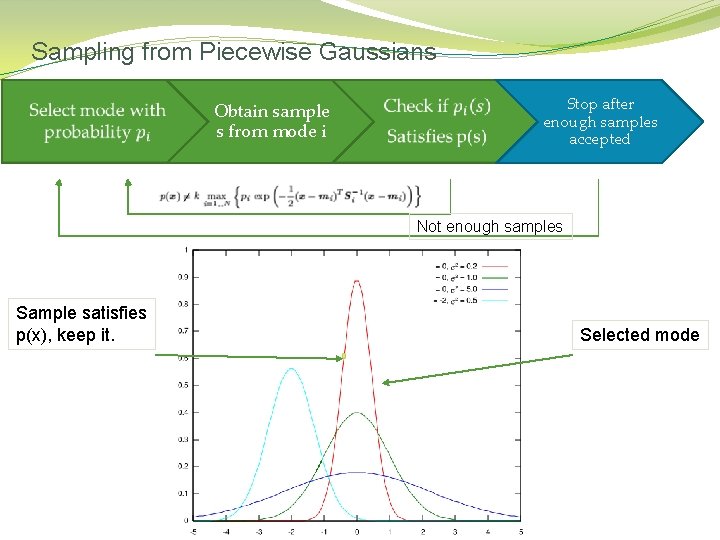
Sampling from Piecewise Gaussians Obtain sample s from mode i Stop after enough samples accepted Not enough samples Sample satisfies p(x), keep it. Selected mode

Template Registration �In order to estimate the likelihood distribution template images of the model should be registered. �This can be done for example by randomizing values for the SPM model chains and rendering a 3 D graphic model of a person then his joints conforms to the model state.

Likelihood Computation We maximize it minimizing the log likelihood: Using Iterative Gauss-Newton method.

Deriving Posterior Distributions �
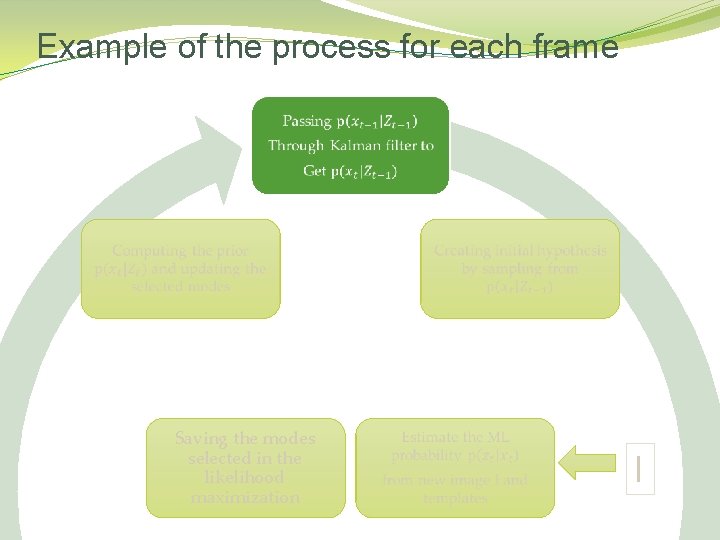
Example of the process for each frame Saving the modes selected in the likelihood maximization I
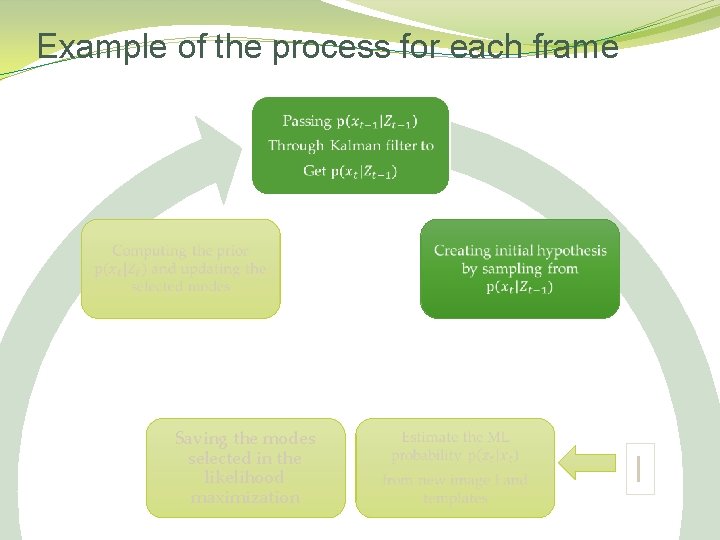
Example of the process for each frame Saving the modes selected in the likelihood maximization I
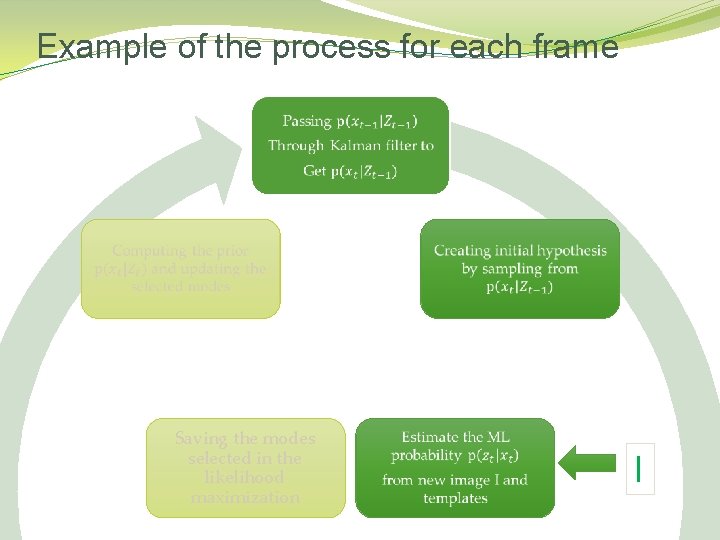
Example of the process for each frame Saving the modes selected in the likelihood maximization I
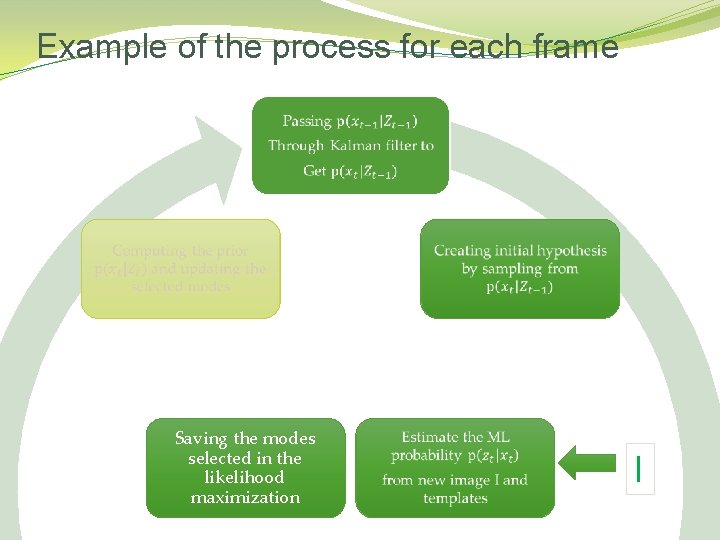
Example of the process for each frame Saving the modes selected in the likelihood maximization I
Example of the process for each frame Saving the modes selected in the likelihood maximization I

Experimental Results �The algorithm was tested on three sequences involving Fred Astaire from the movie ‘Shall We Dance’. A 2 D 19 -DOF SPM model is manually initialized in the first image frame, after which tracking is fully automatic. �First experiment: �Each joint probability distribution in the state-space is described via only 1 mode (unimodal). �Second experiment: �Typically each joint probability distribution in the state-space is described via 10 modes in a PWG representation

Experimental Results �Single hypothesis (tracker initialized with single mode) tracker: The single hypothesis tracker fails to handle the self-occlusion caused by Fred Astaire’s legs crossing

Experimental Results �Multi hypothesis (tracker initialized with 10 modes) tracker: • Top row: the multiple modes of the tracker are shown. • Bottom row: the dominant mode is shown, which demonstrate the ability of the tracker to handle ambiguous situations and thus survive the occlusion event.

References �Plankers and Fua, “Articulated Soft Objects for Video-based Body Modeling”, ICCV 2001 �Cham, T. J. and Rehg, J. M. “A Multiple Hypothesis Approach to Figure Tracking”, CVPR 1999 (II: 239 -245)

The End
- Slides: 76