Arrays Programming The Big Picture n Three fundamental

Arrays

Programming: The Big Picture n Three fundamental ideas to understand use effectively: q flow of control n q modular design n q iteration/conditionals subroutines/recursion data representation n data types/data structures

Data Structures n A data structure is a way of storing data in a computer so that it can be used efficiently q n typically data that is more complex than just a number or a truth value The choice of data structure used to store data can impact the performance of your program

Data Structures n Given a collection of data: q n How do we want to store this? q q q n 1, 1, 5, 3, 1, 5, 4, 1, 1 [4*1, 0*2, 1*3, 1*4, 2*5] {1, 3, 4, 5} [1, 1, 5, 3, 1, 5, 4, 1, 1] Depends on the application q e. g. voting vs. scheduling (bag) (set) (list)

Data Structures n Given a collection of data: q n Do we expect more data? q q n 1, 1, 5, 3, 1, 5, 4, 1, 1 more data arriving at the tail? more data arriving in the middle? All of these factors together should be considered in choosing a data representation

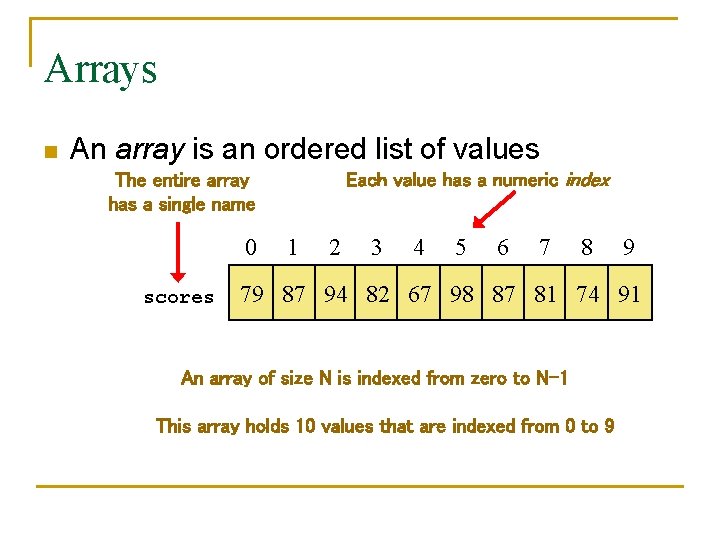
Arrays n An array is an ordered list of values Each value has a numeric index The entire array has a single name 0 scores 1 2 3 4 5 6 7 8 9 79 87 94 82 67 98 87 81 74 91 An array of size N is indexed from zero to N-1 This array holds 10 values that are indexed from 0 to 9

Arrays n A particular value in an array is referenced using the array name followed by the index in brackets n For example, the expression scores[2] refers to the value 94 (the 3 rd value in the array) n That expression represents a place to store a single integer and can be used wherever an integer variable can be used

Arrays n For example, an array element can be assigned a value, printed, or used in a calculation: scores[2] = 89; scores[first] = scores[first] + 2; mean = (scores[0] + scores[1])/2; System. out. println ("Top = " + scores[5]);

Arrays n Limitations: q q n Array length is fixed when the array is created Can only hold a single type so… q q Can’t lengthen an array mid-program Can’t store an int and a String in the same array

Arrays n The values held in an array are called array elements n An array stores multiple values of the same type – the element type n The element type can be a primitive type or an object reference q n arrays of integers, arrays of Strings, arrays of Bank. Accounts In Java, the array itself is an object that must be instantiated

Declaring Arrays n Use the new syntax n To create a pointer to an array, append a [] to the element type q q n String[] names; int[] scores; Like other object types, this creates a reference – not an object

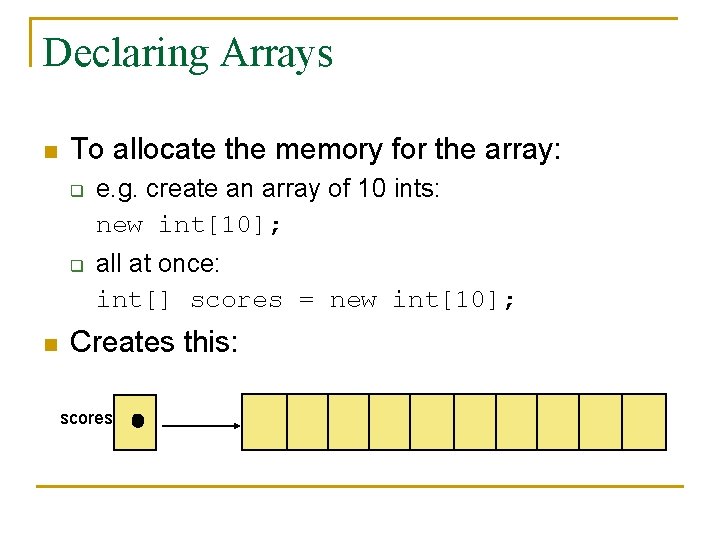
Declaring Arrays n To allocate the memory for the array: q q n e. g. create an array of 10 ints: new int[10]; all at once: int[] scores = new int[10]; Creates this: scores

Declaring Arrays n Note that the type of the variable scores is int[] q n The array type does not specify its size q n An array of integers The type is not an “array of size 10” However, every object of type array has a specified size

Declaring Arrays n Some other examples of array declarations: float[] prices = new float[500]; boolean[] flags; flags = new boolean[20]; char[] codes = new char[1750];

Manipulating Array Elements n Some sample array commands: int[] my. Array = new int[100]; my. Array[0] = 2; my. Array[4] = my. Array[0] + 1; System. out. println(my. Array[4]); \ prints 3 my. Array[99] = 2; \ ok my. Array[100] = 2; \ error

Bound Checking n Array of size N has indices 0, …, N-1 Referencing an element with an index larger than N-1 results in an “Array. Index. Out. Of. Bounds. Exception” n This is called automatic bounds checking n

Bounds Checking n It’s common to produce one-off errors: int[] codes = new int[100]; for (int index=0; index <= 100; index++) codes[index] = index*50 + epsilon; n Solution: use the public length constant and the strictly less than relation

The length Constant n Each array object has a public constant called length that holds the number of elements q n note: not the highest index It is referenced with the array name: e. g. codes. length n So this is a safer loop: for (int index=0; index < codes. length; index++) codes[index] = index*50 + epsilon;

The Iterator for Loop n Can also use the “iterator version” of the for loop: for (int score : scores) System. out. println (score); n This is only appropriate when processing all array elements from top (lowest index) to bottom (highest index)

Alternate Array Syntax n The brackets of the array type can be associated with the element type or with the name of the array n Therefore the following two declarations are equivalent: float[] prices; float prices[]; n The first format generally is more readable and should be used

Initializer Lists n An initializer list can be used to instantiate and fill an array in one step n The values are delimited by braces and separated by commas: int[] units = {147, 323, 89, 933, 540, 269, 97, 114, 298, 476}; char[] letter. Grades = {'A', 'B', 'C', 'D', ’F'};

Initializer Lists n Note that when an initializer list is used: q the new operator is not used q no size value is specified n The size of the array is determined by the number of items in the initializer list n An initializer list can be used only in the array declaration

Arrays as Parameters n n n An entire array can be passed as a parameter Example: the main method takes an argument of type String[] This array is obtained from command-line arguments

Command Line Arguments public class Command. Line. Test { public static void main (String[] args) { System. out. println(“First parameter: “ + args[0]); System. out. println(“Second parameter: + args[1]); } }

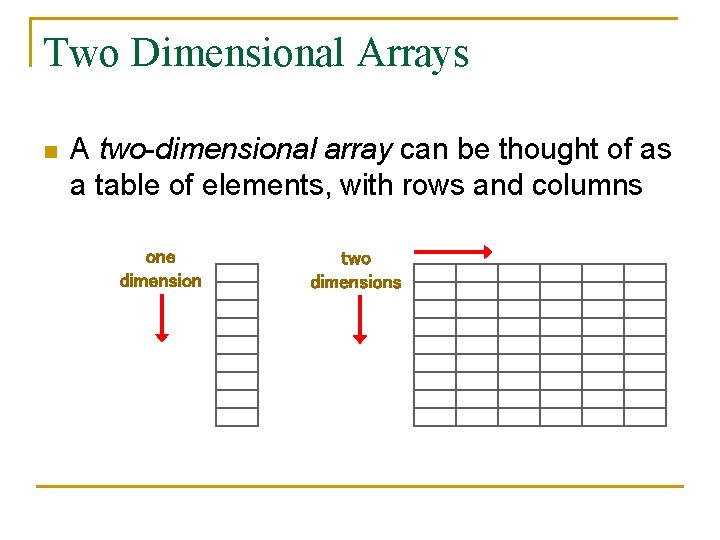
Two Dimensional Arrays n A two-dimensional array can be thought of as a table of elements, with rows and columns one dimension two dimensions

Two Dimensional Arrays n Declared as follows: int[][] scores = int[12][10]; n Elements referenced by pairs: value = scores[4][8]; n n \two bounds to check To be accurate… this is just an array of arrays… not a new type An entire row can be referenced with a single index arrayvariable = scores[4];

The Array. List Class n Included in the java. util package n Essentially, it is an array that can grow and shrink q n add elements and remove elements Another advantage: can store multiple types

The Array. List Class n Example: Array. List lunch = new Array. List(); lunch. add(“apple”); lunch. add(“peanut butter sandwich”); System. out. println(lunch); n n n Creates a new array list Adds two string elements Prints both out (using hidden to. String() )

The Array. List Class n Elements can be inserted or removed with a single method invocation n When an element is inserted, the other elements "move aside" to make room n Likewise, when an element is removed, the list "collapses" to close the gap n The indexes of the elements adjust accordingly

Array. List Efficiency n The Array. List class is implemented using an underlying array n The array is manipulated so that indexes remain continuous as elements are added or removed n If elements are added to and removed from the end of the list, this processing is fairly efficient n But as elements are inserted and removed from the front or middle of the list, the remaining elements are shifted

Searching

Searching n A common problem: find an item in an array q q find exact match find item that contains… return position return element

Linear Search n n In general, we need to go through every element in the array Pseudocode: for i from 0 to length – 1 if array[i]=target : return i return -1 \ indicates target not in array n Java implementation in text

Properties n Will work on any array q q n searches every element will find target if it’s there Problem: it is slow q q searches every element might not be necessary in some arrays

Binary Search n Suppose we have a sorted array q then we can avoid looking at every element -2 q n -1 8 14 17 23 29 37 74 75 81 87 95 We are looking for 17 in this array Half the array can quickly be eliminated q q Look in the middle: 29 Can ignore second half of the array

Details n Keep track of the “candidate” part of the array q q q Look at the middle of the candidate part Found it? DONE! Not found? Throw away one half -2 -1 8 14 17 23 29 37 74 75 81 87 95

Pseudocode first = 0 \ start of candidate array last = length -1 \ end of candidate array while first <= last mid = (first+last)/2 if (array[mid]=target): return mid else if (array[mid] < target): first = mid+1 else if (array[mid] > target): last = mid-1 return -1 \ not in array

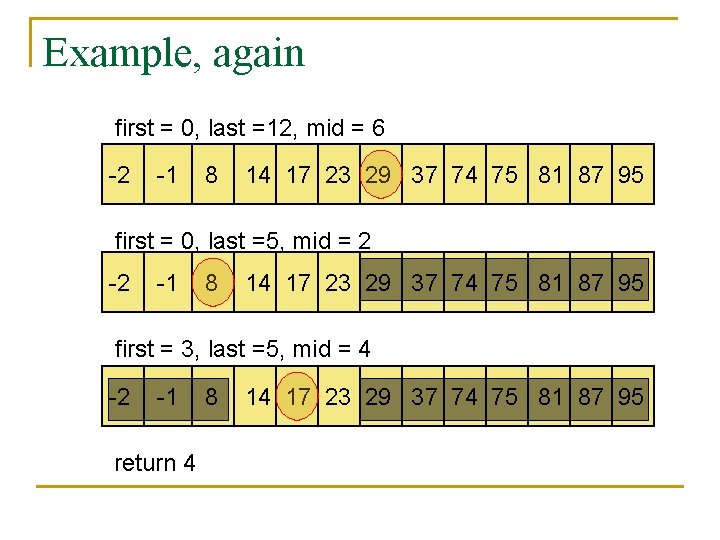
Example, again first = 0, last =12, mid = 6 -2 -1 8 14 17 23 29 37 74 75 81 87 95 first = 0, last =5, mid = 2 -2 -1 8 14 17 23 29 37 74 75 81 87 95 first = 3, last =5, mid = 4 -2 -1 return 4 8 14 17 23 29 37 74 75 81 87 95

Speed n binary search q q n linear search q n example took 3 steps worst case: 4 ( approx. log 2(n) ) worst case: 13 (=n) binary search is much faster for large arrays q q but we need the array to be sorted… how much work does that require…