Array Variable PlaceholderStructure to store a basic unit

Array • Variable: –Placeholder/Structure to store a basic unit of data. –Example: • 1 integer variable stores single integer data. • 1 float variable stores single float data. –Question is: • In a computer, where is that value assigned to a variable stored? –In memory, possibly Random Access Memory (RAM) • But where exactly in memory? –On some physical address in memory because, » Memory is divided in physical locations and, » Each location has a particular address associated with it.

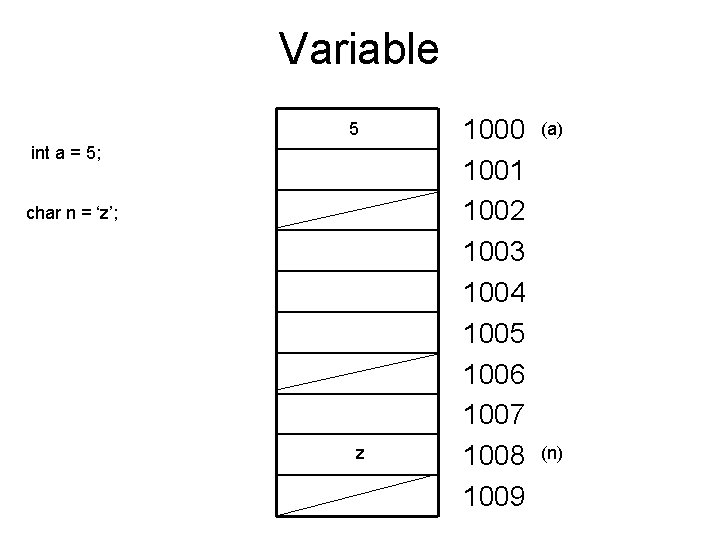
Variable 5 int a = 5; char n = ‘z’; z 1000 1001 1002 1003 1004 1005 1006 1007 1008 1009 (a) (n)

Array • Variable: –Sometimes in our program, • There might be a need to store multiple data of similar type. –Example: • Roll numbers of 10 students. • Marks of DFS of 10 students. – 2 solutions: • Create different variables each having a different name. –int num 1, num 2, num 3 etc. • Create a collection of variables referred by a common name. –int num[3] –This looks much better solution.

Array 5 int a = 5; char n = ‘z’; int num[3] = {11, 10, 20}; 11 10 20 Finite Same data type / Homogeneous z 1000 1001 1002 1003 1004 1005 1006 1007 1008 1009 (a) (num) Ordered (n)

Array • Array: –Finite, Ordered collection of Homogeneous data elements where, • Ordering is maintained by storing all elements in, • Continuous / Contiguous locations of memory. –Properties: • Finite: –Contains only a limited (finite) number of elements. • Ordered: –All elements are stored one by one in continuous / contiguous locations of computer memory. • Homogeneous: –All the elements of an array are of the same data type. –Example: • An array of integers to store the roll numbers of all students in a class. • An array of strings to store the names of all villagers in a village.

Array (Terminologies) Size / Length / Dimension Lower Bound (L) int A[5] = {50, 25, 40, 10, 35} Upper Bound (U) Position (P) Pascal Fortran C Index (i) Ap Base Address (M) Values Address A[i] 1 -3 1 0 50 1000 2 -2 2 1 25 1001 3 -1 3 2 40 1002 4 0 4 3 10 1003 5 1 5 4 35 1004 C Language: int A[5] C Language: int A[0. . . 4] Fortran Language: int A[5] Fortran Language: int A[1. . . 5] Pascal Language: int A[-3. . . 1] (A)

Array (Terminologies) float A[0. . . 5] = {50. 50, 25. 50, 40. 50, 10. 00, 35. 00} Values 50. 50 25. 50 40. 50 10. 00 35. 00 Address Values Address 50. 50 1003 25. 50 1002 1004 40. 50 1004 10. 00 1006 35. 00 1008 1000 2 address locations 1001 2 bytes 1002 1005 1006 1007 1008 1009 Word Size (W)

Array • Terminology: –Size: • Number of elements in an array. • Also called: –Length, Dimension. • Example: –int A[5] » Size is 5. –Type: • Kind of data type it is meant for. • Example: –int A[5] » Type is int. –Base / Base Address (M): • Address of the memory location where the first element of the array is located. • Denoted by symbol M.

Array • Terminology: –Index (i): • Subscript by which the elements in an array can be referenced / accessed. • Always an integer value. • Lower Bound (L): –Starting index of an array. –Denoted by symbol L. • Upper Bound (U): –Ending index of an array. –Denoted by symbol U. • Example: –A[1]: Element located on index 1. –A[-3]: Element located at index -3.

Array • Terminology: –Range of Indices: • Depends on the programming language in which the array is created. –In C, » Index always starts from 0 upto Size-1. –In Fortran, » Index always starts from 1 to Size. –In Pascal, » Index can have user-defined integer values. –Position (P): • Relative rank of an element in the array. • Does not depend on the programming language. • Example: –A 1: First element in the array. –A 5: Fifth element in the array. –Word Size (W): • Size of one element in the array. • Denoted by symbol W.

Array (Answer the Questions) Data: Array A[0. . . 8] Questions: What is the size of A? 9 What is the position of A[4]? 5 What is the index of A 8? 7 What is the address of A[4]? What is the address of A 2? 1016 1004 M = 1000 Position Index 1 0 1000 2 1 1004 3 2 1008 4 3 1012 5 4 1016 6 5 1020 7 6 1024 8 7 1028 9 8 1032 Total memory occupied by A? 9*4 = 36 B Which element is on address 1028? W = 4 B A 8 or A[7] Array A Address

Array (Answer the Questions) Data: Array A[-5. . . 1] Questions: What is the size of A? 7 What is the position of A[-4]? 2 What is the index of A 6? 0 What is the address of A[-1]? 2008 What is the address of A 8? M = 2000 W = 2 B Position Index Array A Address 1 -5 2000 2 -4 2002 3 -3 2004 4 -2 2006 5 -1 2008 6 0 2010 7 1 2012 Incorrect What is the address of A[2]? Incorrect Which element is on address 2004? Element with position 3 / Element with index -3.

Array (Answer the Questions) Data: Array A[-53. . . 101] M = 1517 W = 4 B Questions: What is the size of A? Wait a minute. I’m calculating on fingers. What is the position of A[-4]? One second. What is the index of A 61? You’re confusing me. What is the address of A[-1]? Stop it please. What is the address of A[-54]? Incorrect. Atleast, got 1 right answer. Very difficult to answer because the array seems to be very big. It is difficult to represent the array on paper. Equations are needed to answer these questions.

Array (Formula to calculate Size) Size = U – L + 1 Array A[0. . . 4] L=0 U=4 Array A[1. . . 5] L=1 U=5 Index Array A[-3. . . 2] L = -3 U=2 Index 1 -3 1 2 -2 2 3 -1 3 4 0 5 1 0 4 L U 2 Size(A) = 5 Size(A) = U + 1 - 0 Size(A) = U + 1 -1 Size = 2 – (-3) + 1 Size(A) = U + 1 - L Size = 2 + 3 + 1 = 6 Size = U – L + 1

Array (Formula to calculate Index from Position & vice-versa) Index = i = L + P - 1 Array A[0. . . 4] L = 0, U = 4 Position Index (P) (i) Array A[1. . . 5] L = 1, U = 5 Position Index (P) (i) Array A[-31. . . 20] L = -31, U = 20 Position Index (P) (i) 1 0 1 1 1 -31 2 2 2 -30 3 2 3 3 3 -29 4 3 4 4 4 -28 5 4 5 5 Index(A 1) = 0 Index(A 2) = 1 = 2 - 1 Index(A 3) = 2 = 3 - 1 Index(Ap) = P – 1 + 0 Index(A 1) = 1 Index(A 2) = 2 Index(A 3) = 3 Index(Ap) = P -1 + 1 Index(Ap) = P – 1 + L Find index of 4 th element. Find index of element located at position 4. Find index of A 4. Index = i = L + P - 1 Index = i = -31 + 4 - 1 Index = i = -28

Array (Formula to calculate Address from Index / Position) Address = M + ( i – L ) * W Array A[0. . . 4] L = 0, U = 4, M=1000 Index Address (i) 0 1000 1 1001 2 1002 3 4 Array A[1. . . 5] L = 1, U = 5, M=1000 Index Address (i) 1 1000 Will Word Size (W) matter? 2 1001 Yes 3 1002 1003 4 1003 1004 5 1004 Address(A[0]) = 1000 Address(A[1]) = 1001 = 1000 + 1 Address(A[2]) = 1002 = 1000 + 2 Address(A[i]) = 1000 + i = M + i Address(A[i]) = M + (i - 0) Address(A[i]) = M + ( i – L ) * W Address(A[1]) = 1000 Address(A[2]) = 1001 = 1000 + 1 Address(A[3]) = 1002 = 1000 + 2 Address(A[i]) = 1000 + (i – 1) Address(A[i]) = M + ( i – L ) * W

Array (Formula to calculate Address from Index) Address = M + ( i – L ) * W Array A[-5. . . 1], L = -5, U = 1, M = 1000, W = 4 Index (i) Address -5 1000 Address = M + (i - L) * W -4 1004 Address = 1000 + (-1 – (-5)) * 4 -3 1008 Address = 1000 + (-1 + 5) * 4 -2 1012 -1 1016 0 1020 1 1024 What is the address of element located at index -1? What is the address of A[-1]? Address = 1000 + (4) * 4 Address = 1000 + 16 Address = 1016

Array • Formulas / Equations: –Size = U – L + 1 • U: Upper Bound of the array. • L: Lower Bound of the array. –Index or i = L + P – 1 • L: Lower Bound of the array. • P: Position of element in the array. –Address = M + (i – L) * W • M: Base address of the array. • i: Index of the element. • L: Lower bound of the array. • W: Word size of the array. • Also called: –Indexing Formula • Could also be expressed in the form of Position ‘P’ as: –Address = M + (P – 1) * W » Because (i – L) = (P – 1)

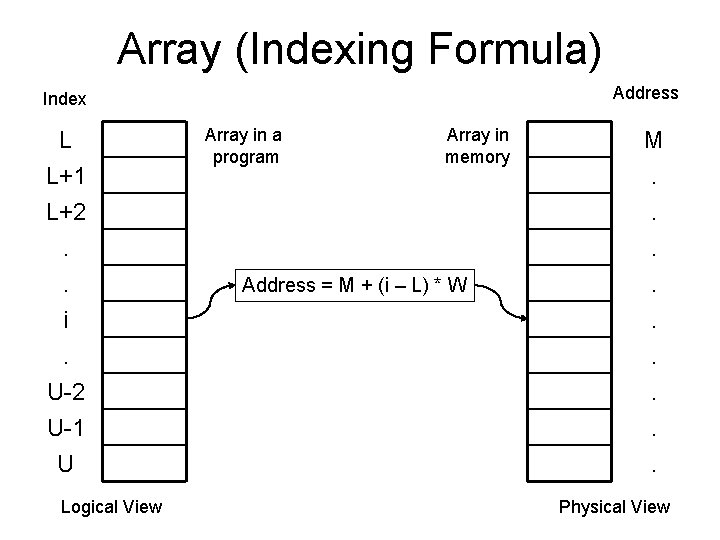
Array (Indexing Formula) Address Index L L+1 L+2. . i. U-2 U-1 U Logical View Array in a program Array in memory Address = M + (i – L) * W M. . Physical View

Array • Question-1: –Suppose, an array A[-15. . . 64] is stored in a memory whose starting address is 459. Assume that the word size for each element is 2. Then obtain the following: • (a) How many number of elements are there in the array A? • (b) How much memory is required to store the entire array? • (c) What is the address location for A[50]? • (d) What is the address location of 10 th element? • (e) Which element is located at address 599?

Array Size = U – L + 1 i=L+P– 1 Address = M + (i – L) * W • Answer-1: Data: L = -15 U = 64 M = 459 W= 2 (a) How many number of elements are there in the array A? Size = U – L + 1 Size = 64 – (-15) + 1 Size = 64 + 15 + 1 Size = 80 80 elements are there in the array A.

Array Size = U – L + 1 i=L+P– 1 Address = M + (i – L) * W • Answer-1: (b) How much memory is required to store the entire array? Total memory required = Size * W Total memory required = 80 * 2 Total memory required = 160 (c) What is the address location for A[50]? i = 50 Address = M + (i – L) * W Address = 459 + (50 – (-15)) * 2 Address = 459 + (50 + 15) * 2 Address = 459 + (65) * 2 Address = 459 + 130 Address = 589 Data: L = -15, U = 64, M = 459, W=2

Array • Answer-1: (d) What is the address location of 10 th element? P = 10 Index or i = L + P - 1 i = -15 + 10 - 1 i = -16 + 10 i = -6 Address = M + (i – L) * W Address = 459 + (-6 – (-15)) * 2 Address = 459 + (-6 + 15) * 2 Address = 459 + (9) * 2 Address = 459 + 18 Address = 477 Size = U – L + 1 i=L+P– 1 Address = M + (i – L) * W Data: L = -15, U = 64, M = 459, W=2

Array Size = U – L + 1 i=L+P– 1 Address = M + (i – L) * W • Answer-1: (e) Which element is located at address 599? Address = 599 Address = M + (i – L) * W 599 = 459 + (i – (-15)) * 2 599 = 459 + (i + 15) * 2 599 = 459 + 2 i + 30 Index or i = L + P - 1 55 = -15 + P - 1 55 + 1 = P P = 71 599 – 459 – 30 = 2 i 2 i = 110 / 2 i = 55 71 st element with index 55 is located on address 599. / A 71 is on address 599. / A[55] is on address 599. Data: L = -15, U = 64, M = 459, W=2

Array Size = U – L + 1 i=L+P– 1 Address = M + (i – L) * W • Question-2: –Suppose, an array A[-51. . . 48] is stored in a memory whose starting address is 1000. Assume that the word size for each element is 4. Then obtain the following: • (a) How many number of elements are there in the array A? • (b) How much memory is required to store the entire array? • (c) What is the address location for A[1]? • (d) What is the address location of 53 rd element? • (e) Which element is located at address 1076?

Array Index Array A 0 1 2 3 4 11 20 9 18 15 Values (Marks of DFS of 5 students) Question: Increment all the values by 1. Some Process/Procedure/Function needs to be done on the array. What is a ‘Process’ then? ‘Process’ is a sequence of steps that is executed to get the work done. Example: Process of making Tea. In Computer terminology, such process is called: ‘ALGORITHM’ / ‘PSEUDOCODE’. When an Algorithm is implemented in a programming language, it is called a: ‘PROGRAM’

Array • Algorithm v/s Program: –Algorithm: • It is not dependent on the programming language. • It does not have to follow the syntax of any programming language. • Should be easily understandable. –Program: • It is dependent on the programming language. • It has to follow the syntax of the programming language in which it is implemented. • Might not be easily understandable.

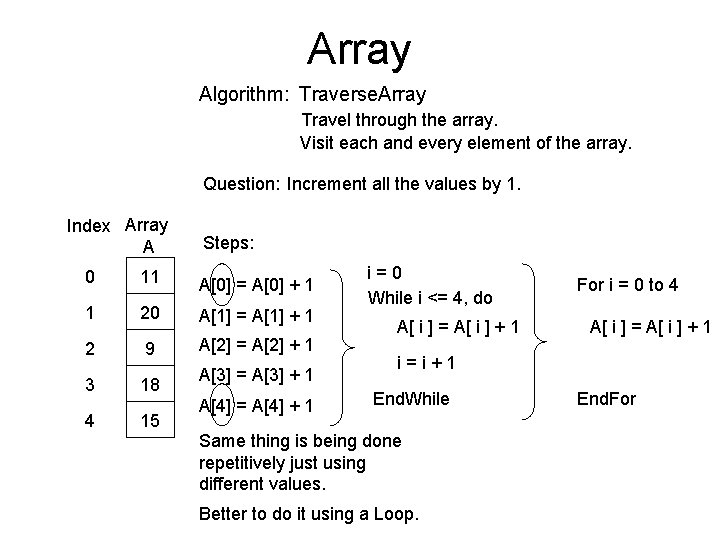
Array Algorithm: Traverse. Array Travel through the array. Visit each and every element of the array. Question: Increment all the values by 1. Index Array A Steps: 0 11 A[0] = A[0] + 1 1 20 A[1] = A[1] + 1 2 9 A[2] = A[2] + 1 3 4 18 15 A[3] = A[3] + 1 A[4] = A[4] + 1 i=0 While i <= 4, do A[ i ] = A[ i ] + 1 For i = 0 to 4 A[ i ] = A[ i ] + 1 i=i+1 End. While Same thing is being done repetitively just using different values. Better to do it using a Loop. End. For

Array Algorithm: Traverse. Array i=0 Iteration-1: Condition 0 <= 4 A[0] = 11+1 = 12 i=0+1=1 Condition 1 <= 4 A[1] = 20+1 = 21 i=1+1=2 True Condition 2 <= 4 A[2] = 9+1 = 10 i=2+1=3 True Condition 3 <= 4 A[3] = 18+1 = 19 i=3+1=4 Iteration-5: Condition 4 <= 4 A[4] = 15+1 = 16 i=4+1=5 Iteration-6: Condition 5 <= 4 True Question: Increment all the values by 1. Index Array A Steps: 0 11 i=0 1 20 While i <= 4, do 2 9 A[ i ] = A[ i ] + 1 3 18 i=i+1 4 15 End. While Check whether this algorithm is working for this array or not. How to check whether an algorithm is working or not? TRACING Iteration-2: Iteration-3: Iteration-4: True False

Array Algorithm: Traverse. Array Index Array A -2 0 11 -1 1 20 0 2 9 1 3 18 2 4 15 Steps: i=0 i=L While i <= 4, do While i <= U, do A[ i ] = A[ i ] + 1 Process( A[ i ] ) i=i+1 End. While Question: Will this algorithm work for any kind of array? Whether C, Fortran, Pascal? Whether Small array, Large array etc? Question: Will this algorithm be able to do any kind of processing?

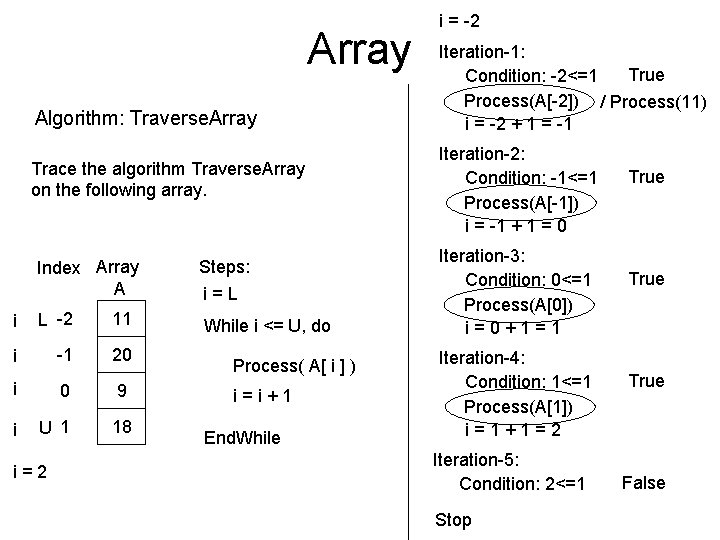
Array Algorithm: Traverse. Array Trace the algorithm Traverse. Array on the following array. Index Array A Steps: i L -2 11 While i <= U, do i -1 20 i 0 9 i U 1 18 i=2 i=L Process( A[ i ] ) i=i+1 End. While i = -2 Iteration-1: True Condition: -2<=1 Process(A[-2]) / Process(11) i = -2 + 1 = -1 Iteration-2: Condition: -1<=1 Process(A[-1]) i = -1 + 1 = 0 Iteration-3: Condition: 0<=1 Process(A[0]) i=0+1=1 Iteration-4: Condition: 1<=1 Process(A[1]) i=1+1=2 Iteration-5: Condition: 2<=1 Stop True False

Array • Algorithm: –Traverse. Array. • Input: –Array A with elements. • Output: –According to Process(). • Data Structure: –Array A[L. . . U]

Array Algorithm: Traverse. Array Steps: i=L While i <= U, do Process( A[ i ] ) i=i+1 End. While Stop

Array Algorithm: Search. Array Question: Search for an element and tell whether it is present in the array or not. Index Array A 0 11 9 1 20 22 2 9 3 18 4 15 Search is successful. Return 2 (Index of 9). Search is unsuccessful. Return NULL. Question: Will Traverse. Array algorithm be used here?

Algorithm: Search. Array KEY = 9 Index Array A i=L Steps: i = 0 , found = 0 , location = NULL While (i <= 4) && (found == 0), do Process If( A[ i ] == (A[ 9 i ])), then 0 11 found = 1 1 20 location = i 2 9 3 18 4 15 (i <= U) End. If i=i+1 End. While If (found == 0), then Question: Is it the most optimized / efficient? Question: Will it work for any array? Question: Will it work for any search value? print “Search is unsuccessful. ” Else print “Search is successful. ” End. If Return(location) If (A[ i ] == KEY)

Trace Algorithm: Search. Array Index Array A Steps: KEY = 20 i = L, found = 0, location = NULL While (i <= U) && (found == 0), do i = -1, found = 0 , location = NULL If( A[ i ] == KEY ), then found = 1 -1 11 0 20 End. If 1 9 i=i+1 2 18 location = i End. While If (found == 0), then print “Search is unsuccessful. ” Else print “Search is successful. ” End. If Return(location) Iteration-1: Condition: -1<=2 && 0==0 True If (11 == 20) False i = -1 + 1 = 0 Iteration-2: Condition: 0<=2 && 0==0 True If (20 == 20) True found = 1 location = 0 i=0+1=1 Iteration-3: Condition: 1<=2 && 1==0 Search is successful Return (0) False

Array • Algorithm: –Search. Array. • Input: –Array A with elements. –KEY: Element to be searched. • Output: –On Success, appropriate message and return Index/Location of KEY in array A. –On Failure, appropriate message and return NULL. • Data Structure: –Array A[L. . . U]

Algorithm: Search. Array Steps: i = L, found = 0, location = NULL While (i <= U) && (found == 0), do If( A[ i ] == KEY ), then found = 1 location = i End. If i=i+1 End. While If (found == 0), then print “Search is unsuccessful. ” Else print “Search is successful. ” End. If Return(location) Stop

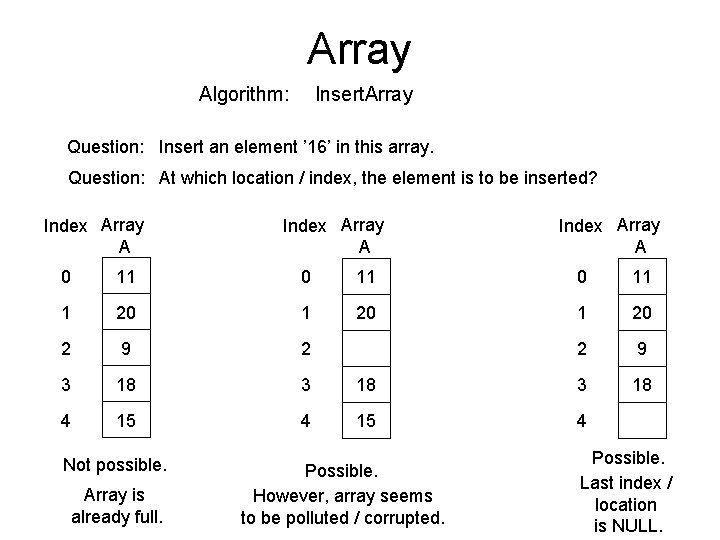
Array Algorithm: Insert. Array Question: Insert an element ’ 16’ in this array. Question: At which location / index, the element is to be inserted? Index Array A 0 11 1 20 2 9 2 2 9 3 18 4 15 4 Not possible. Array is already full. Possible. However, array seems to be polluted / corrupted. Possible. Last index / location is NULL.

Array Algorithm: Insert. Array Question: Insert an element ’ 16’ in this array. Question: At which location / index, the element is to be inserted? 1 Index Array A Solution-1: Index Array A Solution-2: 0 11 Steps: 1 20 16 A[1] = 16 1 20 16 A[4] = A[1] 2 9 3 18 4 20 Stop 4 Does not work. It should be insertion, not updation. A[1] = 16 Stop Does not work. Original sequence is changed, hence polluted.

Array Algorithm: Insert. Array Question: Insert an element ’ 16’ in this array. Question: At which location / index, the element is to be inserted? 1 Index Array A 0 11 1 20 2 20 9 3 9 18 4 18 It seems that the only solution is: Shifting down of elements to make place for the new element. Question: Will downward shifting start from Top or Bottom? i. e. Will 20 be shifted down first or 18 will be shifted down first?

Array Algorithm: Insert. Array Question: Insert an element ’ 16’ in this array. Question: At which location / index, the element is to be inserted? 1 Index Array A 0 11 1 20 2 3 4 Downward Shifting starting from Top. Index Array A 0 11 1 20 9 20 2 9 20 18 3 9 18 4 18 Elements will be lost. So it cannot work. Downward Shifting starting from Bottom. All elements are preserved. So it can work.

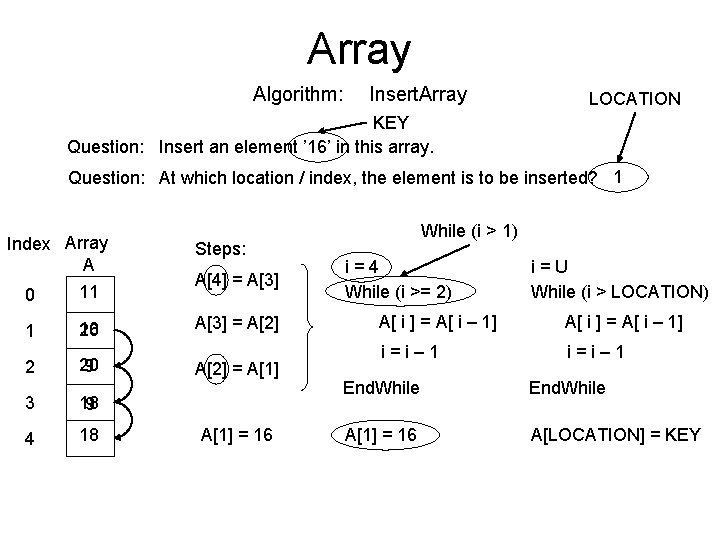
Array Algorithm: Insert. Array LOCATION KEY Question: Insert an element ’ 16’ in this array. Question: At which location / index, the element is to be inserted? 1 Index Array A 0 11 1 16 20 2 20 9 3 18 9 4 18 Steps: A[4] = A[3] = A[2] = A[1] = 16 While (i > 1) i=4 While (i >= 2) i=U While (i > LOCATION) A[ i ] = A[ i – 1] i=i– 1 End. While A[1] = 16 A[LOCATION] = KEY

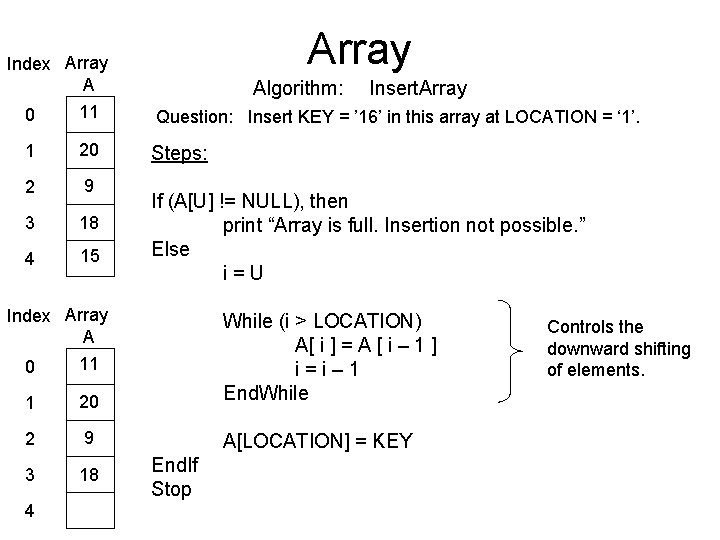
Array Index Array A Algorithm: Insert. Array 0 11 Question: Insert KEY = ’ 16’ in this array at LOCATION = ‘ 1’. 1 20 Steps: 2 9 3 18 4 15 If (A[U] != NULL), then print “Array is full. Insertion not possible. ” Else i=U Index Array A 0 11 1 20 While (i > LOCATION) A[ i ] = A [ i – 1 ] i=i– 1 End. While 2 9 A[LOCATION] = KEY 3 18 4 End. If Stop Controls the downward shifting of elements.

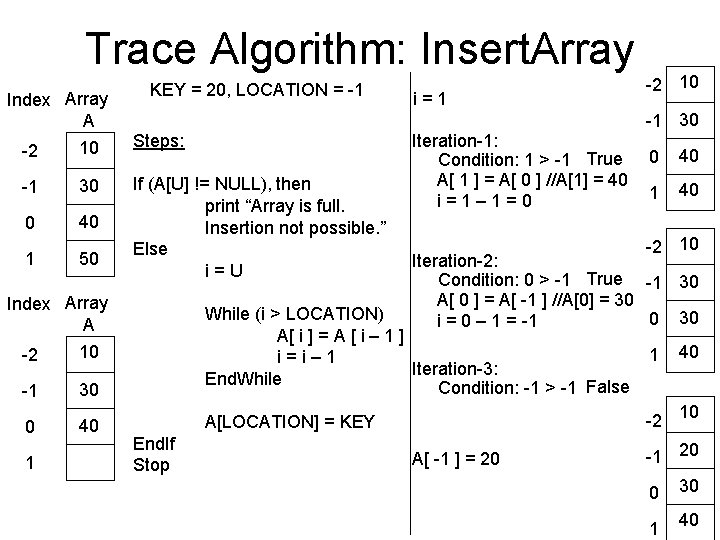
Trace Algorithm: Insert. Array Index Array A KEY = 20, LOCATION = -1 -1 30 -2 10 Steps: -1 30 0 40 If (A[U] != NULL), then print “Array is full. Insertion not possible. ” Else i=U 1 50 i=1 Index Array A Iteration-1: Condition: 1 > -1 True A[ 1 ] = A[ 0 ] //A[1] = 40 i=1– 1=0 10 -1 30 40 A[LOCATION] = KEY 1 40 Iteration-2: Condition: 0 > -1 True -1 30 A[ 0 ] = A[ -1 ] //A[0] = 30 0 30 i = 0 – 1 = -1 -2 End. If Stop 0 -2 10 While (i > LOCATION) A[ i ] = A [ i – 1 ] i=i– 1 Iteration-3: End. While Condition: -1 > -1 False 0 -2 10 A[ -1 ] = 20 40 1 -2 10 -1 20 0 30 1 40

Array • Algorithm: –Insert. Array. • Input: –Array A with elements. –KEY: Element to be inserted. –LOCATION: Index where KEY is to be inserted. • Output: –On Success, Element with value KEY inserted at index LOCATION. –On Failure, appropriate message to be displayed. • Data Structure: –Array A[L. . . U]

Algorithm: Insert. Array Steps: If (A[U] != NULL), then print “Array is full. Insertion not possible. ” Else i=U While(i > LOCATION) A[ i ] = A[ i – 1 ] i=i– 1 End. While A[LOCATION] = KEY End. If Stop

Array • How to convert any algorithm into a ‘C’ program?

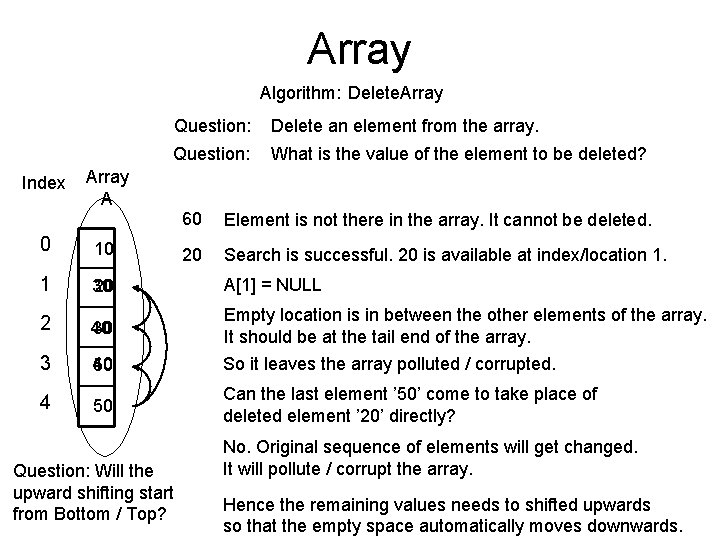
Array Algorithm: Delete. Array Index Question: Delete an element from the array. Question: What is the value of the element to be deleted? Array A 60 Element is not there in the array. It cannot be deleted. 20 Search is successful. 20 is available at index/location 1. 0 10 1 30 20 A[1] = NULL 2 40 30 Empty location is in between the other elements of the array. It should be at the tail end of the array. 3 40 50 So it leaves the array polluted / corrupted. 4 50 Can the last element ’ 50’ come to take place of deleted element ’ 20’ directly? Question: Will the upward shifting start from Bottom / Top? No. Original sequence of elements will get changed. It will pollute / corrupt the array. Hence the remaining values needs to shifted upwards so that the empty space automatically moves downwards.

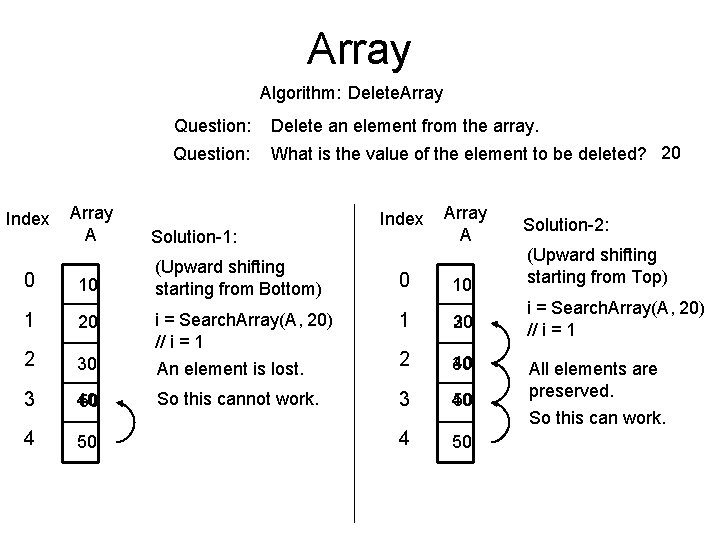
Array Algorithm: Delete. Array Index Array A Question: Delete an element from the array. Question: What is the value of the element to be deleted? 20 Solution-1: Array A Solution-2: 10 (Upward shifting starting from Top) 1 20 30 i = Search. Array(A, 20) // i = 1 An element is lost. 2 40 30 So this cannot work. 3 40 50 4 50 10 (Upward shifting starting from Bottom) 1 20 2 i = Search. Array(A, 20) // i = 1 30 3 40 50 4 50 0 Index 0 All elements are preserved. So this can work.

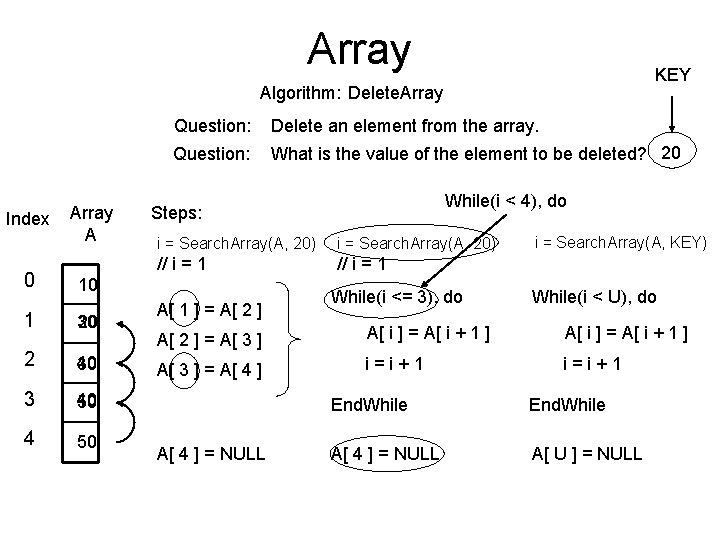
Array KEY Algorithm: Delete. Array Index Array A 0 10 1 30 20 2 40 30 3 40 50 4 50 Question: Delete an element from the array. Question: What is the value of the element to be deleted? 20 While(i < 4), do Steps: i = Search. Array(A, 20) // i = 1 A[ 1 ] = A[ 2 ] While(i <= 3), do i = Search. Array(A, KEY) While(i < U), do A[ 2 ] = A[ 3 ] A[ i ] = A[ i + 1 ] A[ 3 ] = A[ 4 ] i=i+1 A[ 4 ] = NULL End. While A[ 4 ] = NULL A[ U ] = NULL

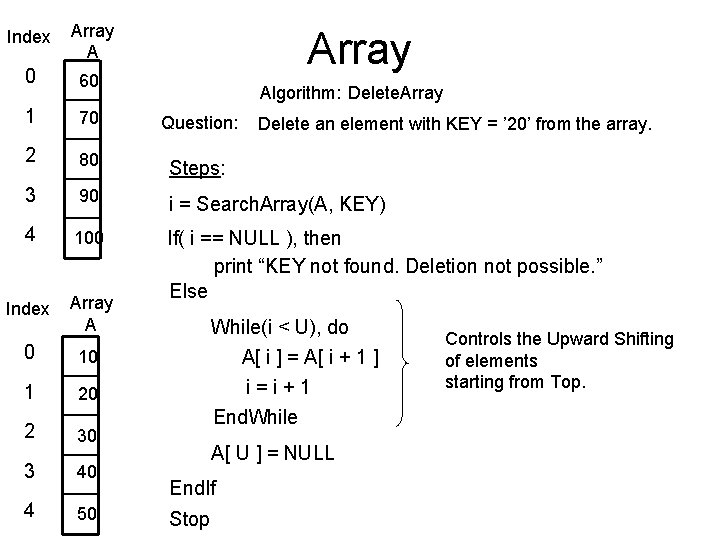
Index Array A 0 60 1 70 Question: 2 80 Steps: 3 90 i = Search. Array(A, KEY) 4 100 Index Array A If( i == NULL ), then print “KEY not found. Deletion not possible. ” Else 0 10 1 20 2 30 3 40 4 50 Array Algorithm: Delete. Array Delete an element with KEY = ’ 20’ from the array. While(i < U), do A[ i ] = A[ i + 1 ] i=i+1 End. While A[ U ] = NULL End. If Stop Controls the Upward Shifting of elements starting from Top.

Trace Algorithm: Delete. Array Index KEY = ’ 22’ Array A Condition: -1 == NULL False -2 44 Steps: -1 55 i = Search. Array(A, KEY) 66 If( i == NULL ), then 77 print “KEY not found. Else Deletion not possible. ” 0 1 While(i < U), do Index -2 -1 i = -1 Array A A[ i ] = A[ i + 1 ] i=i+1 11 End. While 22 A[ U ] = NULL 0 33 End. If 1 44 Stop Iteration-1: Condition: -1 < 1 True A[ -1 ] = A[ 0 ] //A[-1] = 33 -2 11 -1 33 0 33 1 44 -2 11 -1 33 0 44 i = -1 + 1 = 0 Iteration-2: Condition: 0 < 1 True A[ 0 ] = A[ 1 ] //A[0] = 44 i=0+1=1 Iteration-3: Condition: 1 < 1 A[1] = NULL False 1

Array • Algorithm: –Delete. Array. • Input: –Array A with elements. –KEY: Element to be deleted. • Output: –On Success, Element with value KEY deleted from the array. –On Failure, appropriate message to be displayed. • Data Structure: –Array A[L. . . U]

Algorithm: Delete. Array Steps: i = Search. Array(A, KEY) If( i == NULL), then print “KEY not found Deletion not possible. ” Else While(i < U) A[ i ] = A[ i +1 ] i=i+1 End. While A[U] = NULL End. If Stop