Array Store marks of 1 subject DFS for

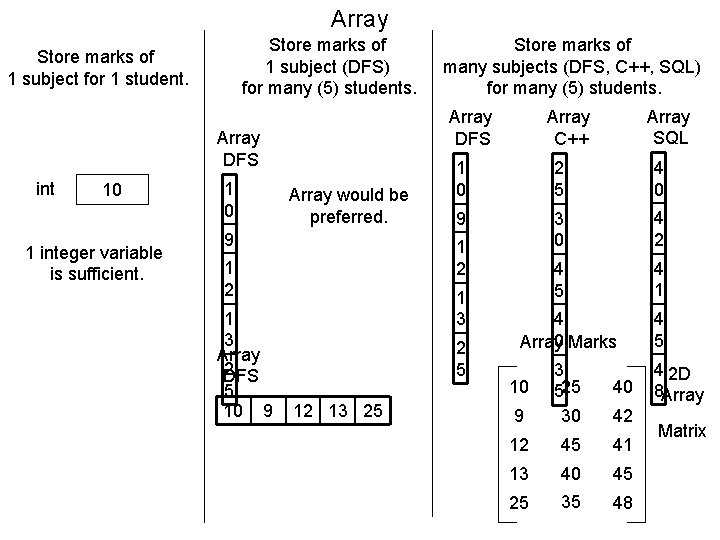
Array Store marks of 1 subject (DFS) for many (5) students. Store marks of 1 subject for 1 student. Array DFS int 10 1 integer variable is sufficient. 1 0 Array would be preferred. 9 1 0 2 5 4 0 9 3 0 4 2 4 5 4 1 1 3 2 5 12 13 25 Array SQL Array C++ 1 2 1 3 Array 2 DFS 5 10 9 Store marks of many subjects (DFS, C++, SQL) for many (5) students. 4 Array 0 Marks 40 9 3 525 30 12 45 41 13 40 45 25 35 48 10 42 4 5 4 2 D 8 Array Matrix

Array • Array: –To store marks of 1 subject for 1 student: • 1 Integer variable is sufficient. –To store marks of 1 subject for many students: • Array would be preferred. – 1 dimensional array is sufficient. –To store marks of many subjects of many students: • Array would be preferred. – 2 -dimensional array / Matrix is required.

Index: A[ i ][ j ] Position: APr. Pc Position Row (Pr) 2 -D Array Col (Pc) 1 2 3 C Col (j) Index 0 Row (i) 1 2 1 0 10 A[0][0] A 11 12 A[0][1] A 12 9 A[0][2] A 13 2 1 11 A[1][0] A 21 5 A[1][1] A 22 2 A[1][2] A 23 10 A[2][0] A 31 3 A[2][1] A 32 15 A[2][2] A 33 3 Array A C: int A[3][3] Fortran: int A[3][3] Pascal: int A[-1. . . 1][1. . . 3] 2 Cols Rows Size 3 x 3 mxn

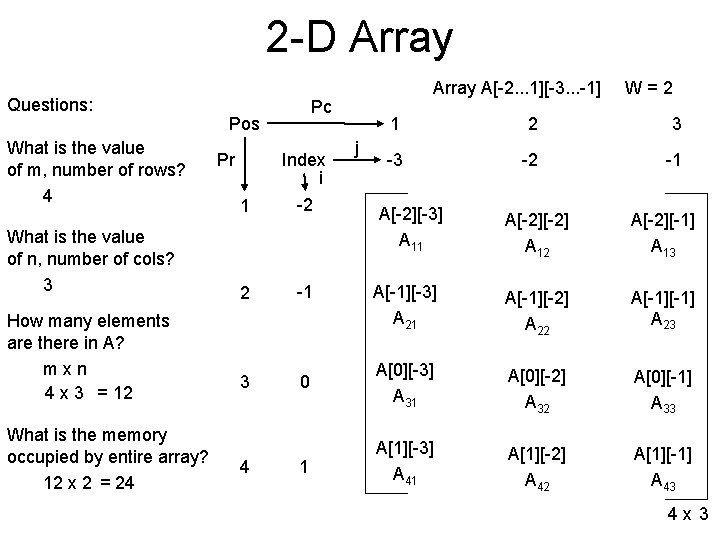
2 -D Array Questions: What is the value of m, number of rows? 4 What is the value of n, number of cols? 3 How many elements are there in A? mxn 4 x 3 = 12 What is the memory occupied by entire array? 12 x 2 = 24 Pc Pos Pr 1 Index i -2 2 -1 3 4 Array A[-2. . . 1][-3. . . -1] j W=2 1 2 3 -3 -2 -1 A[-2][-3] A 11 A[-2] A 12 A[-2][-1] A 13 A[-1][-3] A 21 A[-1][-2] A 22 A[-1] A 23 0 A[0][-3] A 31 A[0][-2] A 32 A[0][-1] A 33 1 A[1][-3] A 41 A[1][-2] A 42 A[1][-1] A 43 4 x 3

2 -D Array A[-23. . . 17][-37. . . 11] Pos Questions: How many elements are there in A? mxn Pr Pc 1 Index i -23 2 -22 3 -21 . . . What is the memory occupied by entire array? Difficult because the array is large. Equations/Formulas are needed again. j W=4 1 2 . . . -37 -36 . . .

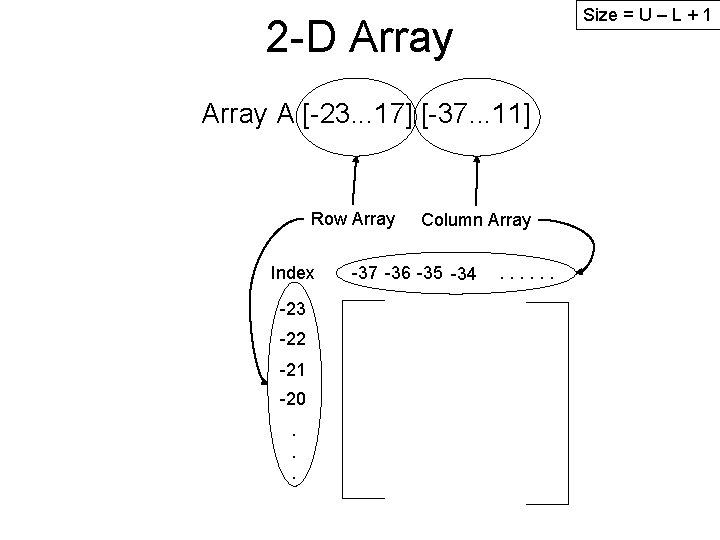
Size = U – L + 1 2 -D Array A [-23. . . 17] [-37. . . 11] Row Array Index -23 -22 -21 -20. . . Column Array -37 -36 -35 -34 . . .

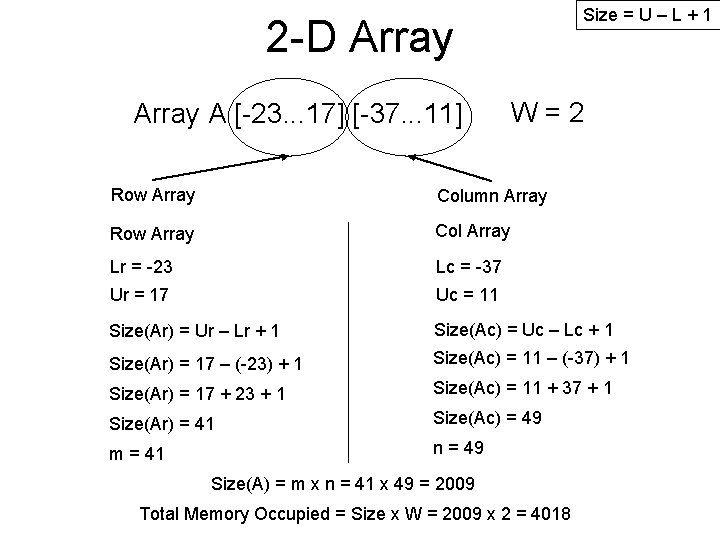
Size = U – L + 1 2 -D Array A [-23. . . 17] [-37. . . 11] W=2 Row Array Column Array Row Array Col Array Lr = -23 Lc = -37 Ur = 17 Uc = 11 Size(Ar) = Ur – Lr + 1 Size(Ac) = Uc – Lc + 1 Size(Ar) = 17 – (-23) + 1 Size(Ac) = 11 – (-37) + 1 Size(Ar) = 17 + 23 + 1 Size(Ac) = 11 + 37 + 1 Size(Ar) = 41 Size(Ac) = 49 m = 41 n = 49 Size(A) = m x n = 41 x 49 = 2009 Total Memory Occupied = Size x W = 2009 x 2 = 4018

Size = U – L + 1 2 -D Array Question: Find out the size and total memory occupied by the array A[-100. . . 99][-5. . . -1] having word size of 4. W=4 Array A [-100. . . 99] [-5. . . -1] Row Array Column Array Lr = -100 Lc = -5 Ur = 99 Uc = -1 Size(Ar) = Ur – Lr + 1 Size(Ac) = Uc – Lc + 1 Size(Ar) = 99 – (-100) + 1 Size(Ac) = -1 – (-5) + 1 Size(Ar) = 99 + 100 + 1 Size(Ac) = -1 + 5 + 1 Size(Ar) = 200 Size(Ac) = 5 m = 200 n=5 Size(A) = m x n = 200 x 5 = 1000 Total Memory Occupied = Size x W = 1000 x 4 = 4000

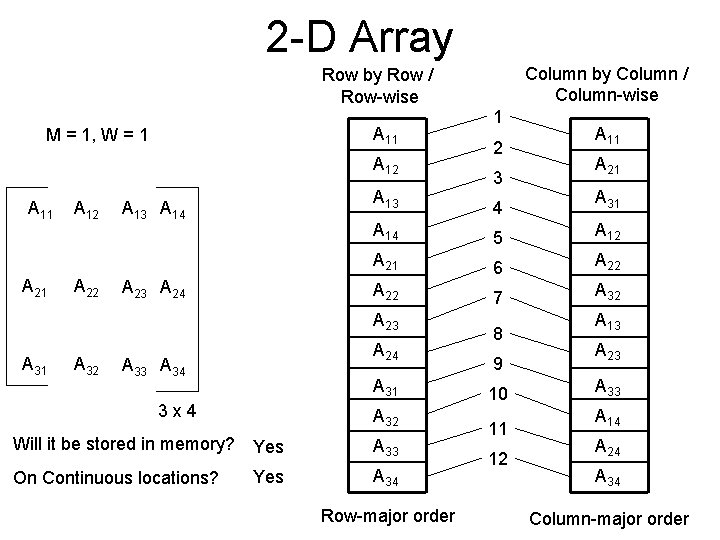
2 -D Array Column by Column / Column-wise Row by Row / Row-wise A 11 M = 1, W = 1 A 12 A 11 A 21 A 12 A 22 A 13 A 14 A 23 A 24 A 32 A 14 5 A 12 A 21 6 A 22 7 A 32 A 31 3 x 4 3 A 21 A 31 A 24 A 33 A 34 2 A 11 4 A 23 A 31 1 A 32 Will it be stored in memory? Yes A 33 On Continuous locations? Yes A 34 Row-major order 8 9 10 11 12 A 13 A 23 A 33 A 14 A 24 A 34 Column-major order

2 -D Array • Memory representation of Matrix / • Storage mechanism of 2 D array: – 2 ways to store a 2 D array / Matrix in memory: • Row-major order: –All elements are stored row by row / row-wise. –Example: » First row, Second row and so on. • Column-major order: –All elements are stored column by column / columnwise. –Example: » First column, Second column and so on.

2 -D Array A[-2. . . 1][-1. . . 1] M = 1000 W = 2 Row Major Order Questions: What is the address location of A[0][0]? 1014 What is the address location of A 33? 1016 What is the address location of A 32? A[-2][-1] A 11 A[-2][0] A 12 A[-2][1] A 13 A[-1] A 21 A[-1][0] A 22 A[-1][1] A 23 A[0][-1] A 31 A[0][0] A 32 A[0][1] A 33 1014 A[1][-1] A 41 A[1][0] A 42 A[1][1] A 43 4 x 3 A 11 1000 A 12 1002 A 13 1004 A 21 1006 A 22 1008 A 23 1010 A 31 1012 A 32 1014 A 33 1016 A 41 1018 A 42 1020 A 43 1022

2 -D Array SPARSE MATRIX Sparse means ‘Not Dense’ / ‘Not Thick’ 10 - - - - - 9 - - - 2 - - - 1 12 - - - 11 Majority of the elements are NULL in this matrix. Storing of NULL elements is a wastage of memory. We need a technique by which only non-null elements are stored.

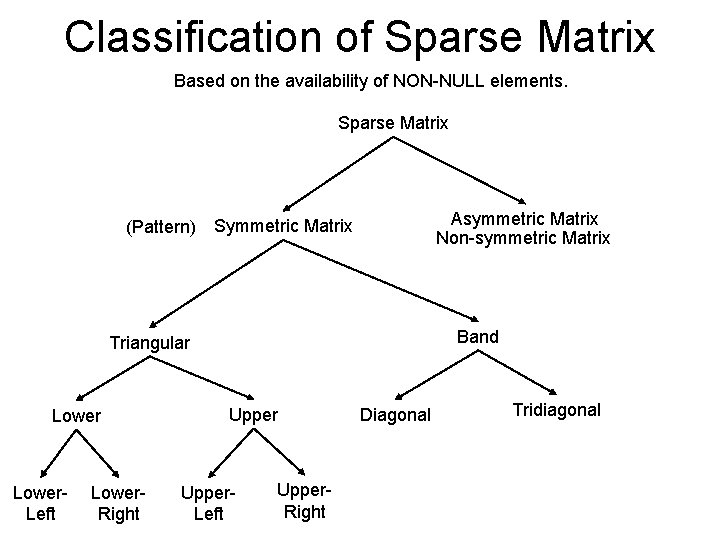
Classification of Sparse Matrix Based on the availability of NON-NULL elements. Sparse Matrix Asymmetric Matrix Non-symmetric Matrix (Pattern) Symmetric Matrix Band Triangular Lower. Left Lower. Right Upper. Left Upper. Right Diagonal Tridiagonal

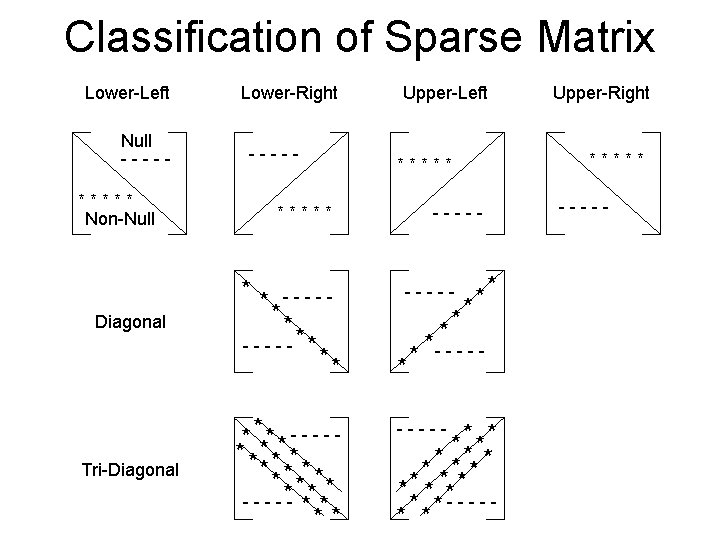
Classification of Sparse Matrix Lower-Left Null ----***** Non-Null Diagonal Tri-Diagonal Lower-Right ----- Upper-Left * * ----** - - -** *** * - - ** * * ----- * * ** ***** ----- ** * * * ----- Upper-Right * ** * *- - * * ** -----

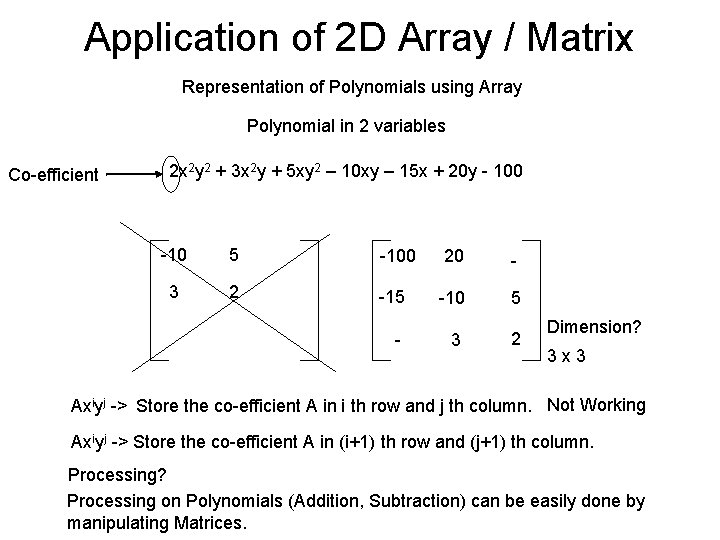
Application of 2 D Array / Matrix Representation of Polynomials using Array Polynomial in 2 variables Co-efficient 2 x 2 y 2 + 3 x 2 y + 5 xy 2 – 10 xy – 15 x + 20 y - 100 -10 5 -100 20 - 3 2 -15 -10 5 - 3 2 Dimension? 3 x 3 Axiyj -> Store the co-efficient A in i th row and j th column. Not Working Axiyj -> Store the co-efficient A in (i+1) th row and (j+1) th column. Processing? Processing on Polynomials (Addition, Subtraction) can be easily done by manipulating Matrices.

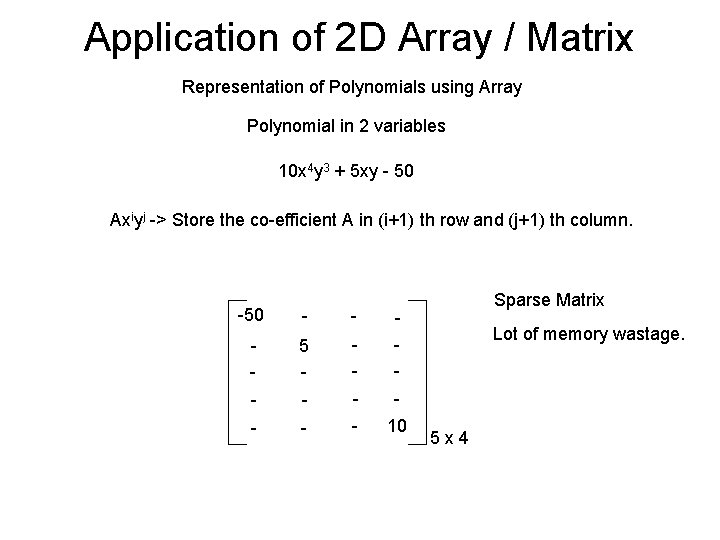
Application of 2 D Array / Matrix Representation of Polynomials using Array Polynomial in 2 variables 10 x 4 y 3 + 5 xy - 50 Axiyj -> Store the co-efficient A in (i+1) th row and (j+1) th column. -50 - - 5 - - - - - 10 Sparse Matrix Lot of memory wastage. 5 x 4