Array Data Structures Algorithms OneDimensional and MultiDimensional Arrays

Array Data Structures & Algorithms One-Dimensional and Multi-Dimensional Arrays, Searching & Sorting, Parameter passing to Functions

Array Data Structures & Algorithms Concepts of Data Collections Arrays in C Syntax Usage Array based algorithms

Concepts of Data Collections Sets, Lists, Vectors, Matrices and beyond

Sets & Lists � The human language concept of a collection of items is expressed mathematically using Sets �Sets are not specifically structured, but structure may be imposed on them �Sets may be very expressive but not always easily represented � Example: The set of all human emotions. � Lists are representations of sets that simply list all of the items in the set �Lists may be ordered or unordered. �Some useful lists include data values and the concept of position within the list. �Example representations: { 0, 5, -2, 4 } { TOM, DICK } First Second

Vectors, Matrices and beyond Many examples of lists arise in mathematics and they provide a natural basis for developing programming syntax and grammar Vectors are objects that express the notion of direction and size (magnitude) The 3 -dimensional distance vector D has components { Dx, Dy, Dz } along the respective x, y and z axes, with magnitude D = sqrt(Dx 2+Dy 2+Dz 2) We use descriptive language terminology such as The x’th component of D . . . Or, D-sub-x

Vectors, Matrices and beyond �Higher dimensional objects are often needed to represent lists of lists. �Matrices are one example that sometimes can be represented in tabular form � 2 -dimensional tables (row, column) � 3 - and higher are hard to visualize, but are meaningful �Beyond this, mathematics works with objects called tensors and groups (and other entities), and expresses the access to object members (data values) using properties and indices based on topologies (loosely put, shape structures)

Vectors, Matrices and beyond �In this course we focus on an introduction to the basic properties and algorithms associated with vectors and matrices, and lists (later) �These objects are mathematically defined as ordered, structured lists �The ordering derives from the property that each element of the list exists at a specific position �Enumerated starting at 0 and incrementing by 1 to a maximum value �The structure determines the mechanism and method of access to the list and its member elements

Arrays in C Syntax Memory structure Usage Functions

Arrays in C Syntax How to declare and reference 1 D arrays using subscript notation Memory structure How is RAM allocated – the meaning of direct access through subscripting Usage Some simple illustrative examples Functions How to deal with arrays as function arguments

Arrays in C - Syntax �Consider the array declarations � int Student. ID [ 1000 ] ; float Mark [ 1000 ] ; char Name [ 30 ] ; �Each of the declarations defines a storage container for a specific maximum number of elements �Up to 1000 Student (integer) ID values �Up to 1000 (real) Marks �A Name of up to 30 characters

Arrays in C - Syntax Each array is referred to by its declared name float A [ 100 ] ; . . . where A refers to the entire collection of 100 storages On the other hand, each separate element of A is Note: referenced the subscript notation Although using a bit clumsy in human natural language, we can change our use of language so that A[K] always refers to the K’th element (not K+1), always A[0] = 12. 34 ; /* assign 12. 34 to the first element */ starting from 0 as the 0’th element. /* NOTE: subscripts always start from 0 */ A[K] = 0. 0 ; /* assign 0 to the (K+1)’th element */

Arrays in C - Syntax It is not necessary to initialize or reference all elements of an array in a program Unlike scalar variables declared as primitive data types, these uninitialized, non-referenced array elements are not flagged as warnings by the compiler There are good reasons to declare arrays of larger size than might be required in a particular execution run of a program At the outset, design the program to accommodate various sizes of data sets (usually acquired as input), up to a declared maximum size This avoids the need to modify and recompile the program each time it is used.

Arrays in C Syntax #define directives are normally located at the beginning of the program This is asource good time introduce another compiler code, toafter #include directives, and prebefore processor directive, #define: function prototypes and the main function. In the example, definedexpression symbol MAX_SIZE, #define is usedby to using definethe constant symbols in C changes to SIDThe andvalue Markof array sizes can be by programs. such symbols is accomplished that they localize simply changing the modification. value assigned to MAX_SIZE and positions of program recompiling. Example: #define MAX_SIZE 1000 int main ( ) { } int SID [ MAX_SIZE ] ; float Mark [ MAX_SIZE ] ; . . .

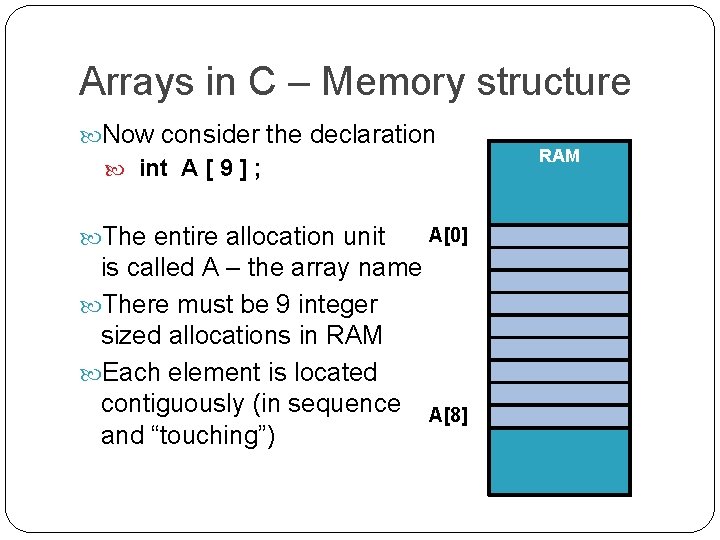
Arrays in C – Memory structure Now consider the declaration int A [ 9 ] ; The entire allocation unit A[0] is called A – the array name There must be 9 integer sized allocations in RAM Each element is located contiguously (in sequence A[8] and “touching”) RAM

The sizeof, operator is a compile-time operator (not an executable instruction or operator) that determines the RAM storage size allocated to a data structure. � Arrays often called When sizeofare is applied to a primitive data type, it provides the direct access size of storage allocated storage, in bytes. RAM containers Try running a program with statements such as: int sizeof � The reference to A[K] is printf( translated “The by sizethe of int is %d bytesn”, A[0] sizeof int ) ; Arrays in C – Memory structure compiler to �First, calculate the RAO relative address offset K * sizeof int �Second, add RAO to A[ K ] base address of A, or simply &A[0] � &A[K] == &A[0] + K*sizeof int Direct Access : : Since the cost of the address computation is always the same (constant) and it provides the actual RAM address location where the data is stored. 0 1 K

Arrays in C – Usage Referencing arrays is straightforward using the subscript notation B = A[ 5 ] ; /* assign 6 th element of A to B */ A [ J ] < A [ K ] /* relational expression */ B = 0. 5*( A[J] – A[J-1] ); /* finite difference */ printf( “%d %d %dn”, A[0], A[mid], A[N-1] ) ; scanf ( “%d%lf%lf”, &N, &R[K], R ) ; /* Note */

Arrays in C – Average vs Median Problem: Input N real numbers and find their average and median. Assume the values are already sorted from lowest to highest Assume no more than 1000 values will be inputted Solution: Declarations float X [1000], Sum, Ave, Median ; int N, Mid ;

Arrays in C – Average vs Median Declarations float A [1000], Sum = 0. 0, Ave, Median ; int N, Mid, K ; Input Data printf( “Enter number of values in list “ ) ; scanf( “%d”, &N ) ; /* Enter all real values into array X */ for( K=0; K < N; K++ ) { scanf( “%f”, &A[K] ) ; /* NOTE: & must be used */ Sum += A[K] ; }

Arrays in C – Average vs Median Compute Average and Median Ave = Sum / (float) N ; /* real division */ Mid = N / 2 ; /* (integer) midpoint of list */ Median = A [ Mid ] ; Report results printf( “Average = %”, Ave ); printf( “Median = %fn”, Median );

Arrays in C – Related arrays Problem: Obtain student marks from testing and store the marks along with ID numbers Assume marks are float and IDs are int data types Solution – Related arrays Define two arrays, one for IDs and one for marks int SID [ 100 ] ; float Mark [ 100 ] ; Coordinate input of data (maintain relationships) for( K = 0 ; K < N ; K++ ) scanf( “%d%f”, &SID[K], &Mark[K] ) ;

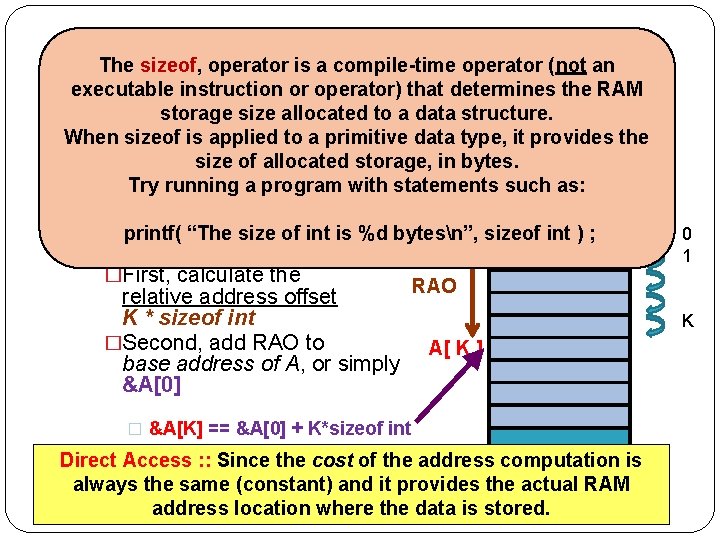
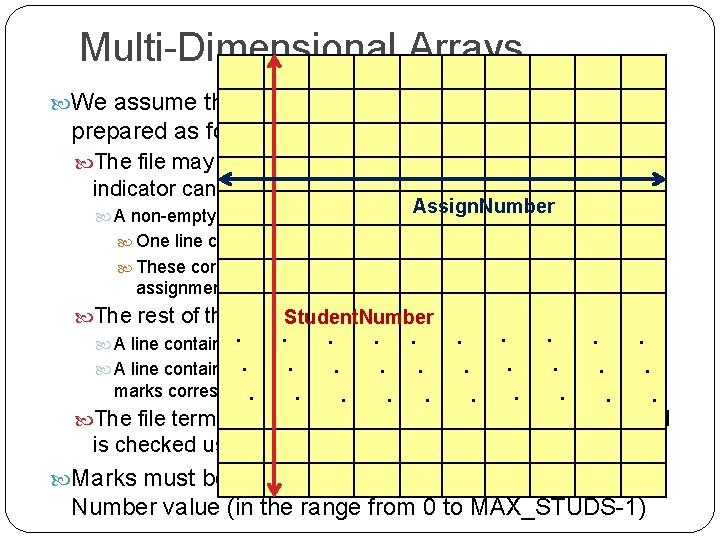
U Arrays in C – Functions Passing arrays as parameters in functions requires some V care and some understanding. We begin with an example. U. V Calculate the dot product of two 3 -vectors U and V. Components: U[0], U[1], U[2] V[0], V[1], V[2] Mathematics: The dot product is defined as Dot. Prod( U, V ) : : = U[0]*V[0] + U[1]*V[1] + U[2]*V[2] Since the dot product operation is required often, it would make a useful function.

Arrays in C – Functions Solution function: double Dot. Prod 3 ( double U[3], double V[3] ) { return U[0] * V[0] + U[1] * V[1] + U[2] * V[2] ; } Note the arguments which specify that arrays of type double with exactly three (3) elements will be passed. Note that the limitation to 3 elements is reflected in the design of the function name: Dot. Prod 3

Arrays in C – Functions Extend this to dot product of N-dimensional vectors: double Dot. Prod. N ( double U[ ], double V[ ], int N ) { double DPN = 0. 0 ; int K ; for( K = 0 ; K < N ; K++ ) DPN += U[K] * V[K] ; return DPN ; } Note the array arguments do not specify a maximum array size. This provides flexibility of design since now the function can handle any value of N. It is up to the programmer to ensure that the actual input arrays and N conform to the assumptions.

Arrays in C – Functions An alternative to the same code is to use pointer references: double Dot. Prod. N ( double * U, double * V, int N ) { double DPN = 0. 0 ; int K ; for( K = 0 ; K < N ; K++ ) DPN += U[K] * V[K] ; return DPN ; } Note the array arguments are now expressed as pointer references. This maintains the same flexibility as previously.

Pointers are not the same as int’s ! Arrays in C – Functions If A is an int (say, 5), then A++ always evaluates to the next A final alternative to the same is to use(ie. pointer (or successor) valuecode in sequence 6). references altogether: On the other hand, if P is a pointer (say, int *, with value &A[K]), then P++ evaluates next (or *successor) double Dot. Prod. N ( doubleto*the U, double V, int N ) {value in sequence, which is usually the next element of an array (ie. double DPN = 0. 0 ; &A[K=1]). int K ; for( K = 0 ; K < N ; K++, U++, V++ ) DPN += *U * *V ; return DPN ; } The U and V variables are address pointers to the array components. U++ and V++ perform the action of updating the pointers by an amount equal to the size of the array data type (in this case double is usually 8 bytes), thus pointing to the next array component in sequence.

Arrays in C – Functions The previous examples have illustrated the various ways that are used to pass array arguments to functions. double Dot. Prod 3 ( double U[3], double V[3] ); double Dot. Prod. N ( double U[ ], double V[ ], int N ); double Dot. Prod. N ( double * U, double * V, int N ); There are important differences When the size of the array is specified explicitly (eg. double U[3]) , some C compilers will allocate storage space for all array elements within the function stack frame If arrays are declared within the function body, they are almost always allocated within the stack frame When the array size is not stated explicitly, a pointer to the array is allocated (much smaller in size than the entire array)

Arrays in C – Functions C compilers may perform code and storage optimization Th Create the most efficient executable code e or within stack frames, a By allocating array storage significant amount of wasted space occurs due to e tic allocations avoidable duplication of storage It also follows that a wastage of a time occurs since it is necessary to copy data from arrays declared in the l calling point code to arrays declared in the called point. Create the most efficient use of RAM storage Pointers solve most of these problems (with a small, but acceptable, increase in processing time) Optimization is a difficult problem and is still the subject of much research

Array Based Algorithms Searching Sorting Very practical !

Array Based Algorithms Searching How to locate items in a list Simplicity versus speed and list properties Sorting Putting list elements in order by relative value Promoting efficient search

Search Algorithms Searching is a fundamentally important part of working with arrays Example: Given a student ID number, what is the Mark they obtained on the test? Do this for all students who enquire. Constructing a good, efficient algorithm to perform the search is dependent on whether the IDs are in random order or sorted. Random order – use sequential search Sorted order – use divide-and-conquer approach

Search Algorithms - Random PROBLEM If a list is 1: stored in random order a possible No guarantee that rand() produce a result and exit thein search technique is will to look at the list elements for loop, especially if the item does not exist. random order search PROBLEM 2: int srch. ID, K an ; array element position will be It is possible that accessed has your not had printf(that “Enter SIDdata “ ) ; stored (will stop the program as “%d”, an error – uninitialized data access violation). scanf( &srch. ID ); for( K=rand() % N ; srch. ID != SID[ K ] ; K=rand() % N ) ; printf( “SID = %d, Mark = %fn”, SID[K], Mark[K] );

Search Algorithms Linear The Linear Search algorithm starts at the beginning of Note that the loop is controlled by two conditions: proceeds sequence: Ifthe a listand is stored in in random order a better search (1) K<N • technique This demands that K beatinitialized at the beginning of is to look the list elements in order, K =0 ; (K=0) /* start at beginning of list */ the list from beginning of the of listtheuntil the element is { the /* ensures search the list */ • do It also that traversal list stops at the end ( srch. ID ==list SID[ Kelements ] ) the break ; are /* array exit loop found –logical or the list exhausted ofifthe (since actual sizeifmay be */ K++ ; /* move to next position */ larger) }srch. ID while (!=KSID[K] < N ) ; /* stop at end of list */ (2) int srch. ID, K, N = 100 ; /* Assume 100 elements */ • This ensures that as soon as the value is found, the loop printf( “Enter your SID “ ) ; These canimmediately, be combinedthereby in a single for structure as is exited avoiding unnecessary scanf( “%d”, &srch. ID ) ; shown below. work /* Perform the search */ for( K=0; K<N && srch. ID != SID[ K ] ; K++ ) ; if( K<N ) printf( “SID = %d, Mark = %fn”, SID[K], Mark[K] );

Search Algorithms - Linear Since this search approach considers each element of the list in sequence, it is called Sequential, or Linear, search. In any situation where the list being searched does not contain the value being searched for, all N elements must be considered This is called the “worst case” scenario However, element willthe beactual foundruntime. . . The term Linear when derivesthe from the fact that performance of the algorithm, in terms numbers distinct The “best case” occurs when weof actually findofthe value CPU operations, is the expressed as a formula like: looked for in first position considered The “average case” refers to the statistical average T = A*N + B obtained over many searches of the list Thisthe is clearly justfor N/2 aelements considered This is just equation line (recall: y = mx + c)

To appreciate the improvement, consider cases where srch. ID will not be located in SID. Search Algorithms - Linear For a statistical spread of srch. ID values (some big, some small) on In cases where the list is sorted, the search algorithm average, only N/2 comparisons are required to eliminate the need to can be improved upon. . further. search Assume that SID is sorted in ascending order The previous algorithm always requires N comparisons to ensure srch. ID NOT in the This is /* Perform the list. search */ version algorithm, on average, only needs N/2 for( comparisons. The complexity algorithms is still K=0; K<N && srch. ID > SID[ of K ]both ; K++ ); O(N), however, because we ignore the coefficient of N. if( K<N && srch. ID == SID[ K ] ) printf( “SID = %d, Mark = %fn”, SID[K], Mark[K] ); Always examine code carefully to ensure that the logic properly accounts for all circumstances that can arise, both positive and negative.

Search Algorithms - Efficiency The time complexity (efficiency, or cost) of an algorithm is important in programming design Algorithmic efficiencies can be divided into several categories, depending on various properties of the problem under consideration NP-complete (computable in finite time) NP-hard (computable in principle, but requires special care and may not actually execute in reasonable time) NP-incomplete (not guaranteed to execute in finite time, contains unknowable aspects) “NP” refers to the way that an algorithm performs and is expressed as a polynomial which may also include functions (such as exponential or logarithm)

Search Algorithms - Efficiency Many problems are characterized by parameters that describe the nature of the data set, or the number of operations that must be performed to complete the algorithm Search problems assume a data set of size N For the Sequential Search algorithm (over N values) K = 0 ; 1 store do { if ( Value == Search. Value ) break ; 2 fetch, 1 compare, 1 branch K++ ; 1 fetch, 1 increment, 1 store } while ( K < N ) ; 2 fetch, 1 compare, 1 branch /* Report result */ R (constant) operations /* In the worst case, all N loops are completed */ Cost : : N * ( 5 fetch + 1 store + 1 increment + 2 compare + 2 branch ) + R + 1 store

The Big O notation in this case is expressed as Search Algorithms Efficiency Time Complexity : : = O( N ) for F(N) K Assume that the behaviour of an algorithm (ie. how long it takes to execute)we is described a function F(N)is that Alternatively, say – theby. Order of F(N) NK counts the number of operations required to complete the algorithm. Note that we ignore the leading coefficient (a. K) of NK, Consider the polynomialof in its N: magnitude. regardless F(N) = a. K NK + a. K-1 NK-1 +. . . + a 1 N + a 0. . . As N increases to very large values, the smallest terms, those with smaller powers (exponent) of N become less relevant (regardless of the size of coefficient a. K) Rather than using complicated polynomial formulas to describe algorithmic time cost, a more convenient notation has been developed – the BIG “O” (Order) notation.

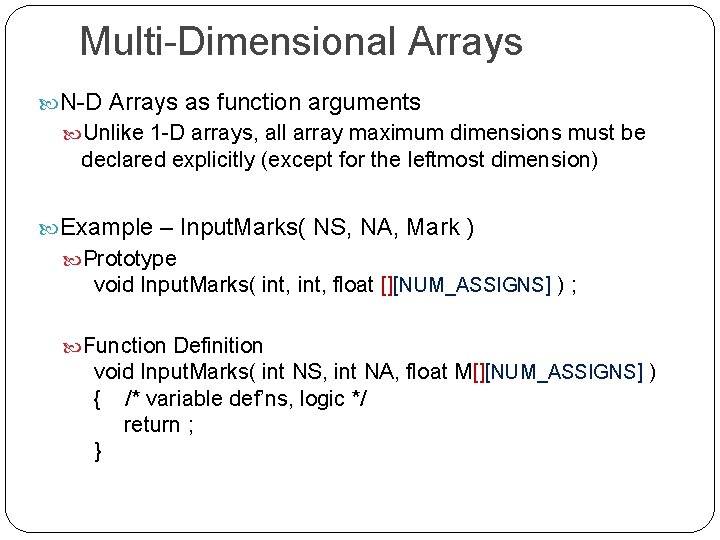
Search Algorithms - Binary Let us now consider a list V of N values where the elements V[K] are sorted in ascending order (from smallest to largest) V[0] < V[1] <. . . < V[N-2] < V[N-1] Problem: Find if/where the search value VS is in V We develop the Binary Search algorithm Our design technique is based on the principle of Divide and Conquer Also called Binary Subdivision

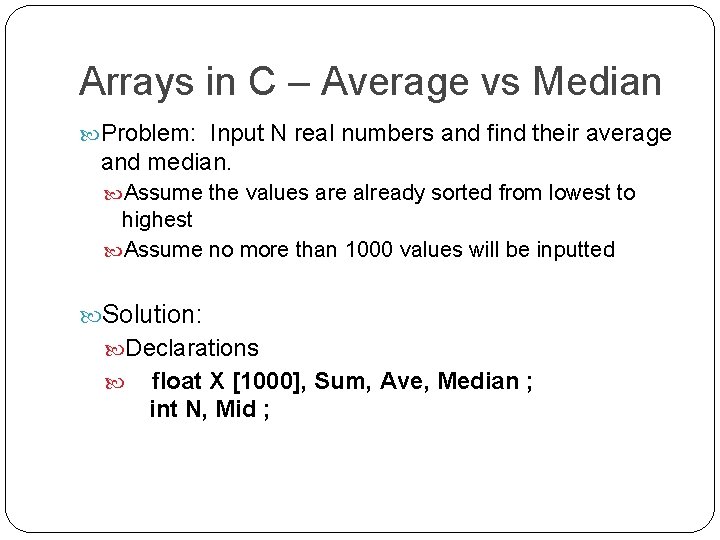
Search Algorithms – Binary A[0] Our strategy involves the idea of sub- list. A sub-list is simply a smaller part of a list. By dividing a list into two sub-lists (where each sub-list contains contiguous values that are sorted) it is possible to quickly eliminate one of the sub-lists with a single comparison. A[Mid] A[Mid+1] Thereafter, we focus attention on the remaining sub-list – but, we reapply the same divide and conquer technique. A[N-1] S U B L I S T

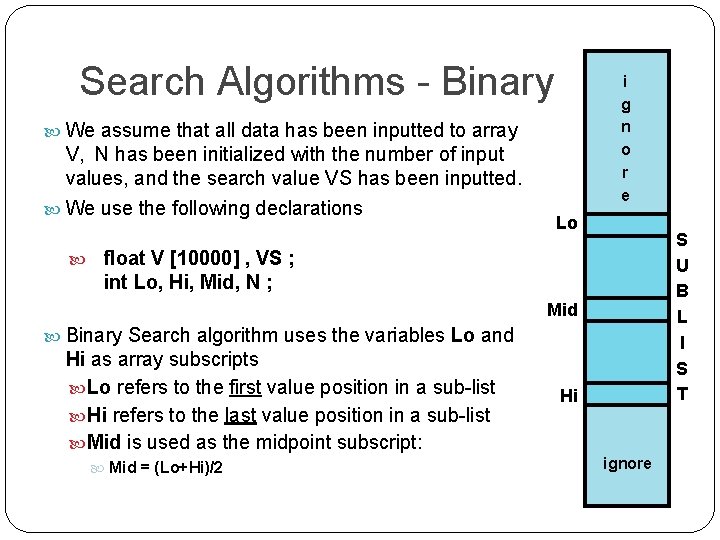
Search Algorithms - Binary i g n o r e We assume that all data has been inputted to array V, N has been initialized with the number of input values, and the search value VS has been inputted. We use the following declarations Lo S U B L I S T float V [10000] , VS ; int Lo, Hi, Mid, N ; Mid Binary Search algorithm uses the variables Lo and Hi as array subscripts Lo refers to the first value position in a sub-list Hi refers to the last value position in a sub-list Mid is used as the midpoint subscript: Mid = (Lo+Hi)/2 Hi ignore

Search Algorithms - Binary Search algorithm: Lo = 0; Hi = N-1 ; /* Use full list as sub-list */ do { Mid = ( Lo + Hi ) / 2 ; /* int division */ if( VS == V[Mid] ) break ; if( VS > V[Mid] ) Lo = Mid + 1 ; Mid else Hi = Mid – 1 ; } while ( Lo <= Hi ) ; ? ? ? printf( “Search value %f “, VS ) ; Hi if ( VS == V[Mid] ) printf( “found at position %dn”, Mid ); else printf( “not foundn” ) ; Lo VS VS VS S U B L I S T

Search Algorithms - Binary To understand the complexity assume a data set of 256 values. We consider the worst case scenario. Size of data set 256 128 64 32 16 8 4 2 1 Step # 1 N = 256 = 28, 2 so it has taken 8+1 = 9 3 steps to prove that VS 4 does not exist in V. 5 6 In general, for a list of 7 size N = 2 K, it takes K+1 8 steps, or O( log 2 N ) 9 Once we split the sub-list to size 1 we clearly determine that the list cannot contain the search value.

Search Algorithms - Binary In general, for a list of size N = 2 K, it takes K+1 steps, or O( log 2 N ) time complexity K is just the logarithm (base-2) of N The efficiency of the Binary Search algorithm is logarithmic, or O( log N ). Some people prefer to say O ( log 2 N), but they are mathematically identical

Search Algorithms The relative efficiencies, or complexities, of the various search algorithms is clearly established when N is large, and for the worst case scenarios. Random Sequential (Linear) Divide & Conquer (Binary) O( >N ? ) O( N ) O( log N ) In the best case, any search algorithm may be T successful after only one (1) probe i m Usually, e one is interested in worst case and average case in choosing an algorithm. N

Sorting Algorithms . . order Puttingthings. Putting in order in. .

Sorting Algorithms From our discussion of binary search we understand the need for the data to be ordered within lists in order to promote fast searching using Binary Search It is also important to understand that not every list should be sorted – study each case carefully Sorting algorithms are designed to perform the ordering required There are literally hundreds of specialized sorting algorithms, with varying efficiencies We will focus on a sorting algorithm called Selection Sort

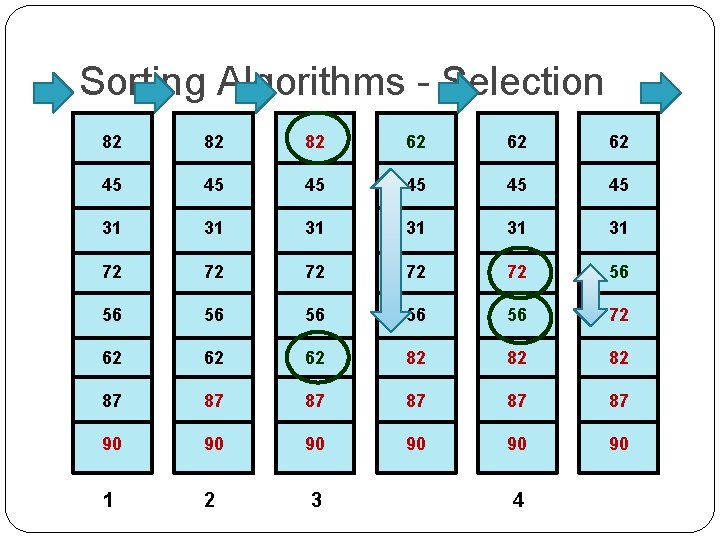
Sorting Algorithms - Selection Sort relies on being able to find the largest 82 (or smallest) element in a sublist Each time the proper value is found, it 45 is exchanged with the element at the end of the sublist 31 We re-apply this technique by shrinking the size of the 72 sublist, until there is no remaining sublist (or a sublist of size 1 element – which is already sorted). 56 We consider the example. . 62 87 90

Sorting Algorithms - Selection 82 82 82 62 62 62 45 45 45 31 31 31 72 72 72 56 56 56 72 62 62 62 82 87 87 90 90 90 1 2 3 4

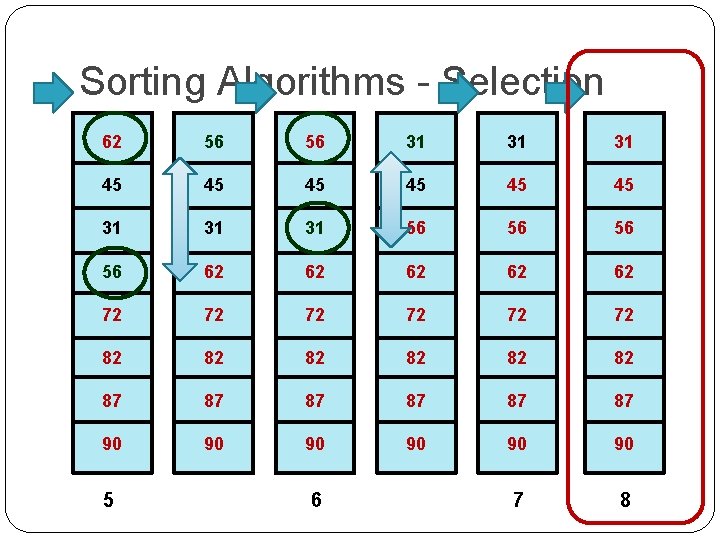
Sorting Algorithms - Selection 62 56 56 31 31 31 45 45 45 31 31 31 56 56 62 62 62 72 72 72 82 82 82 87 87 87 90 90 90 7 8 5 6

Sorting Algorithms - Selection From the example we note that the final step 8 is not actually required, since a sub-list of one (1) element is automatically sorted (by definition). Hence, it took 7 steps to complete the sort. In general, for a list of size N elements, it takes N-1 steps. Each step consists of two parts: First, search an unordered sub-list for the largest element The size of the sub-list is N-K for step K (starting from K=0) Second, exchange (swap) the largest element with the last element in the sub-list Upon completion of each step it should be noted that the sorted sub-list grows by one element while the unsorted sub-list shrinks by one element.

Sorting Algorithms - Selection Start with a sub-list of N unsorted values, and a sub-list 0 31 of 0 sorted values. 45 The unsorted sub-list has subscripts in the subrange [0. . N-1] The sorted sub-list has subscripts in the subrange [N. . N] which 56 is not occupied physically (hence, it does not exist, it is the empty set) 62 72 For K from 0 to N-1, in increments of 1, perform Search the unordered sub-list [0. . N-1 -K] for the largest value 82 and store its position P Exchange the largest element with the last element in the 87 sublist using positions P and N-1 -K. N-1 90 /* The exchange adds the largest element to the beginning of (N-1 -K) the sorted sub-list, while removing it from the end of the unsorted sub-list */

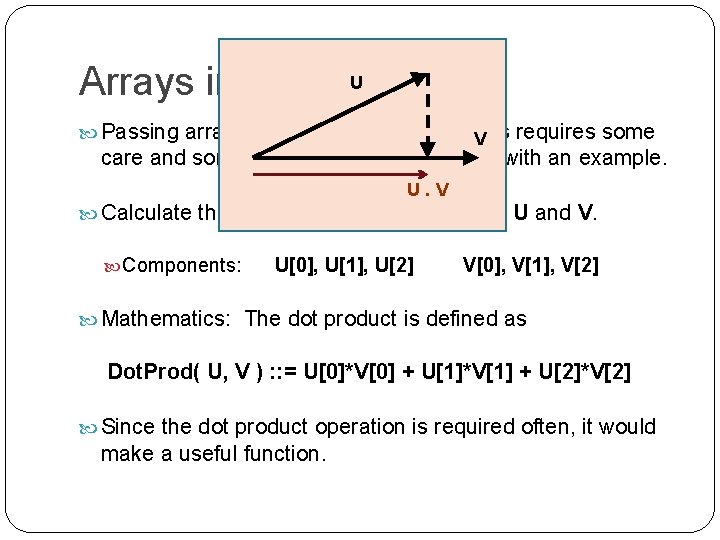
Sorting Algorithms - Selection void Selection. Sort ( double List[ ], int of N array ) { elements Swapping } must be done with some care int J, K, P ; and thought. Three statements double Temp ; are required, and a temporary for( J = 0 ; J < N-1 ; J++ ) { storage variable must be used. P=0; Temp 62 for( K = 0 ; K < N - J ; K++ ) if( List[P] < List[K] ) P = K ; 1 Temp = List[P] ; 62 56 List[P] = List[N-1 -J] ; 3 List[N-1 -J] = Temp ; 2 } List[N-1 -J] 56 62

/* Define a dswap function */ void dswap ( double * A, double * B ) { double T ; T = *A ; *A = *B ; *B = T ; void Selection. Sort ( double List[ ], int N ) { return ; int J, K, P ; } Sorting Algorithms - Selection } double Temp ; for( J = 0 ; J < N-1 ; J++ ) { P=0; for( K = 0 ; K < N - J ; K++ ) if( List[P] < List[K] ) P = K ; Temp = List[P] ; List[P] (=&List[P], List[N-1 -J] ; dswap &List[N-1 -J] ); List[N-1 -J] = Temp ; }

Sorting Algorithms - Selection void Selection. Sort ( double List[ ], int N ) { } int J, K, P ; How many operations must be double Temp ; performed? for( J = 0 ; J < N-1 ; J++ ) { Sum from J = 0 to N-2 P=0; Sum from K = 0 to N-1 -J for( K = 0 ; K < N - J ; K++ ) Core loop logic (Core. Ops) if( List[P] < List[K] ) P = K ; Gauss dealt with this problem Temp = List[P] ; and developed several formulae which bear his name. List[P] = List[N-1 -J] ; List[N-1 -J] = Temp ; In this case the answer is: } ½ N ( N – 1 ) Core. Ops

Sorting Algorithms - Selection The maximum number of operations required to sort a list of N elements in ascending order is ½ N ( N – 1 ) Core. Ops The Core. Ops consist of several fetches, one comparison and either 1 or 2 assignments (stores) This is, essentially, a constant value Thus, the time complexity of the Selection Sort algorithm is O( N 2 )

Sorting Algorithms There are many other sorting algorithms Bubble. Sort Insertion. Sort Quick. Sort Merge. Sort Some of these are iterative, while others are recursive. A number of sorting algorithms exhibit time complexities of O( N 2 ), but some achieve better efficiencies (eg. O( N log N ) ) under certain circumstances. Additional algorithms will be discussed later in 60 -141 and other computer science courses

Bubble Sort The name “Bubble” sort is taken from the rising of the elements at the bottom of the list towards the top of the list, just like bubbles in a boiling pot. void Bubble. Sort ( double List[ ], int N ) { int J, K ; for( J = 0 ; J < N-1 ; J++ ) for( K=0; K<N-J-1; K++ ) if( List[K] < List[K+1] ) dswap( &List[K], &List[K+1] ) ; return ; } J=0 K=0 5 1 1 1 1 5 5 5 3 3 6 6 6 3 3 3 5 5 3 3 3 6 6 6 K=1 K=2 J=1 K=0 J=2 Done!

Other Array Applications One-dimensional arrays are used in many fields of science, Recommendation mathematics, engineering for Learningand almost any subject for which computational simulation is involved Some students experience difficulties learning mathematical concepts, from Computer Graphics and Gaming algebra to statistics. Physics and Chemistry Programming the techniques will Financial modeling greatly improve understanding and help accounting to cement the concepts with a Business foundation based on application and In all cases it is important to understand practice. the role that vectors play (conceptually and theoretically) in addition to simply using arrays as storage containers Typically, mathematical properties are used to develop algorithms and also to determine which algorithms are the best (optimal) choice in particular circumstances.

Example usage for calling: Recursive Binary Search P = Bin. Search( VS, V, 0, N-1 ) ; if( P ==Search -1 ) Binary can be expressed very elegantly using printf( “Value %lf not found”, VS ) ; recursion else printf( “Value %lf found at position %dn”, VS, P ) ; int Bin. Search ( float VS, float V[ ], int Lo, int Hi ) { } int Mid ; if( Lo > Hi ) return -1 ; Mid = ( Lo + Hi ) / 2 ; if( VS == V[Mid] ) return Mid ; if( VS < V[Mid] ) return Bin. Search( VS, V, Lo, Mid-1 ); else return Bin. Search( VS, V, Mid+1, Hi );

Recursive Functions Many algorithms are beautifully and elegantly expressed using recursion Programming recursion requires some experience to perfect, however it is considered a more natural way of thinking to most humans It is true, in general, that any iterative algorithm can be expressed as a recursive algorithm – and vice versa. In practice, it is not so obvious ! Students will be tested on recursion.

Towers of Hanoi Problem: Move all plates from A to either B or C, such that at all times smaller plates are on top of larger plates. A B C

Towers of Hanoi Problem: Move all plates from A to either B or C, such that at all times smaller plates are on top of larger plates. A B C

Towers of Hanoi Problem: Move all plates from A to either B or C, such that at all times smaller plates are on top of larger plates. A B C

Towers of Hanoi Problem: Move all plates from A to either B or C, such that at all times smaller plates are on top of larger plates. A B C

Towers of Hanoi Problem: Move all plates from A to either B or C, such that at all times smaller plates are on top of larger plates. A B C

Towers of Hanoi Problem: Move all plates from A to either B or C, such that at all times smaller plates are on top of larger plates. A B C

Towers of Hanoi Problem: Move all plates from A to either B or C, such that at all times smaller plates are on top of larger plates. A B C

Towers of Hanoi Problem: Move all plates from A to either B or C, such that at all times smaller plates are on top of larger plates. A B C

Towers of Hanoi Problem: Move all plates from A to either B or C, such that at all times smaller plates are on top of larger plates. A B C

Towers of Hanoi Problem: Move all plates from A to either B or C, such that at all times smaller plates are on top of larger plates. A B C

Towers of Hanoi Problem: Move all plates from A to either B or C, such that at all times smaller plates are on top of larger plates. A B C

Towers of Hanoi Problem: Move all plates from A to either B or C, such that at all times smaller plates are on top of larger plates. A B C

Towers of Hanoi Problem: Move all plates from A to either B or C, such that at all times smaller plates are on top of larger plates. A B C

Towers of Hanoi Problem: Move all plates from A to either B or C, such that at all times smaller plates are on top of larger plates. A B C

Towers of Hanoi Problem: Move all plates from A to either B or C, such that at all times smaller plates are on top of larger plates. A B C

Towers of Hanoi Problem: Move all plates from A to either B or C, such that at all times smaller plates are on top of larger plates. A B C

Towers of Hanoi Problem: Move all plates from A to either B or C, such that at all times smaller plates are on top of larger plates. A B C

Towers of Hanoi Problem: Move all plates from A to either B or C, such that at all times smaller plates are on top of larger plates. A B C

Towers of Hanoi Problem: Move all plates from A to either B or C, such that at all times smaller plates are on top of larger plates. A B C

Towers of Hanoi Problem: Move all plates from A to either B or C, such that at all times smaller plates are on top of larger plates. A B C

Towers of Hanoi Problem: Move all plates from A to either B or C, such that at all times smaller plates are on top of larger plates. A B C

Towers of Hanoi Problem: Move all plates from A to either B or C, such that at all times smaller plates are on top of larger plates. A B C

Towers of Hanoi Problem: Move all plates from A to either B or C, such that at all times smaller plates are on top of larger plates. A B C

Towers of Hanoi Problem: Move all plates from A to either B or C, such that at all times smaller plates are on top of larger plates. A B C

Towers of Hanoi Problem: Move all plates from A to either B or C, such that at all times smaller plates are on top of larger plates. A B C

Towers of Hanoi Problem: Move all plates from A to either B or C, such that at all times smaller plates are on top of larger plates. A B C

Towers of Hanoi Problem: Move all plates from A to either B or C, such that at all times smaller plates are on top of larger plates. A B C

Towers of Hanoi Problem: Move all plates from A to either B or C, such that at all times smaller plates are on top of larger plates. A B C

Towers of Hanoi Problem: Move all plates from A to either B or C, such that at all times smaller plates are on top of larger plates. A B C

Towers of Hanoi Problem: Move all plates from A to either B or C, such that at all times smaller plates are on top of larger plates. A B C

Towers of Hanoi Problem: Move all plates from A to either B or C, such that at all times smaller plates are on top of larger plates. A B C

Towers of Hanoi Problem: Move all plates from A to either B or C, such that at all times smaller plates are on top of larger plates. !! DONE !! A B C

Towers of Hanoi Base Case 1 : : Move plate from A to B A B C

Towers of Hanoi Base Case 1 : : Move plate from A to B Hanoi ( A, B, C, 1 ) ; /* Move from A to B, C not used */ A B C

Towers of Hanoi Base Case 2 : : A B C

Towers of Hanoi Base Case 2 : : Move top plate from A to C A B C

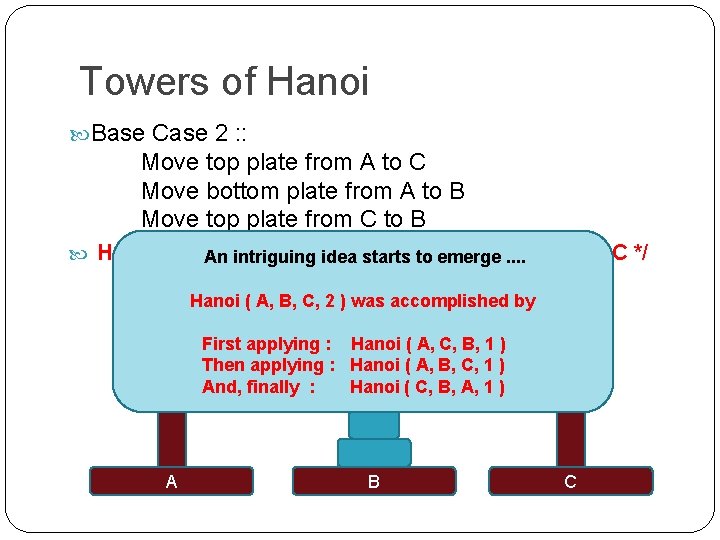
Towers of Hanoi Base Case 2 : : Move top plate from A to C Move bottom plate from A to B A B C

Towers of Hanoi Base Case 2 : : Move top plate from A to C Move bottom plate from A to B Move top plate from C to B Hanoi ( A, An B, intriguing C, 2 ) ; /*idea Move from A to B, starts to emerge. . but use C */ Hanoi ( A, B, C, 2 ) was accomplished by First applying : Hanoi ( A, C, B, 1 ) Then applying : Hanoi ( A, B, C, 1 ) And, finally : Hanoi ( C, B, A, 1 ) A B C

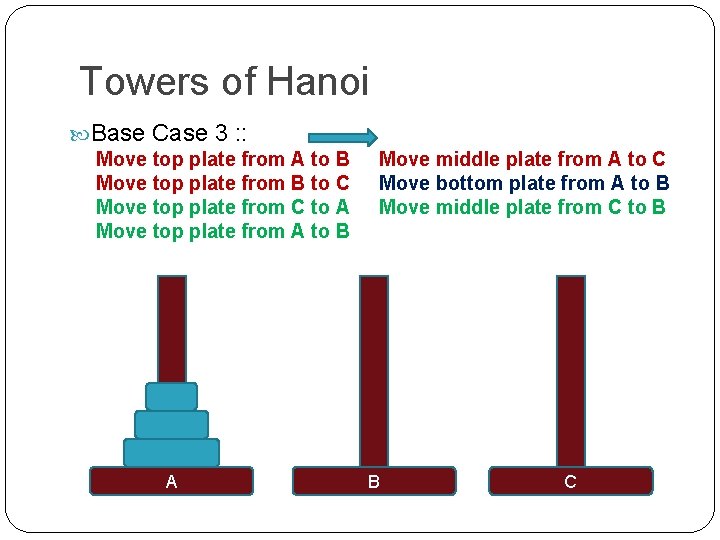
Towers of Hanoi Base Case 3 : : Move top plate from A to B Move top plate from B to C Move top plate from C to A Move top plate from A to B A Move middle plate from A to C Move bottom plate from A to B Move middle plate from C to B B C

Towers of Hanoi Base Case 3 : : Move top plate from A to B Move top plate from B to C Move top plate from C to A Move top plate from A to B A Move middle plate from A to C Move bottom plate from A to B Move middle plate from C to B B C

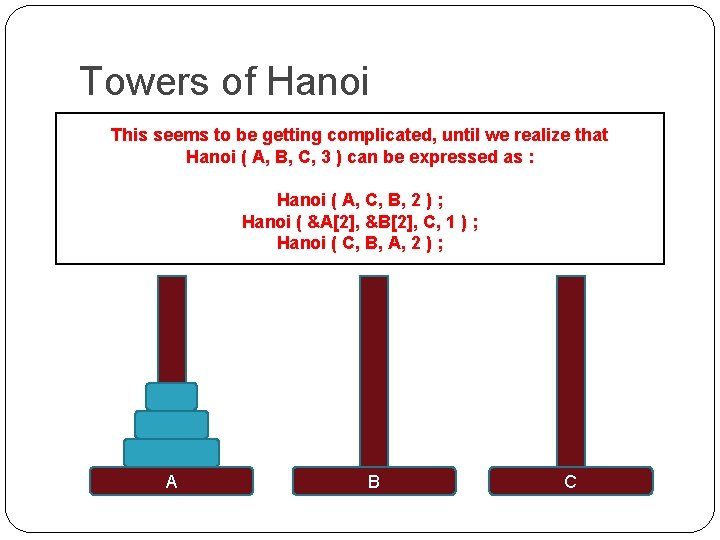
Towers of Hanoi Base 3 : : be getting complicated, until we realize that This Case seems to Hanoifrom ( A, B, C, B 3 ) can be expressed as from : Move top plate A to Move middle plate A to C Move top plate from B to C Move bottom plate from A to B C, B, 2 ); Move top plate from Hanoi C to A( A, Move middle plate from C to B Hanoi ( &A[2], &B[2], C, 1 ) ; Move top plate from A to B Hanoi ( C, B, A, 2 ) ; A B C

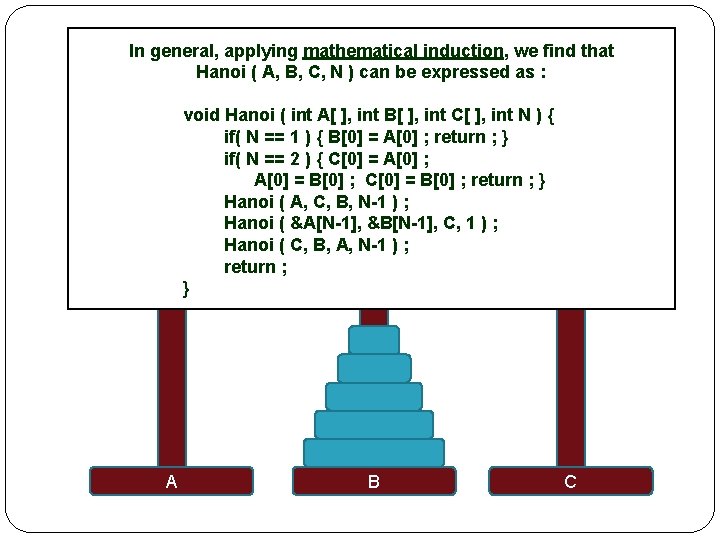
In general, applying mathematical induction, we find that Hanoi ( A, B, C, N ) can be expressed as : Towers of Hanoi void Hanoi ( int A[ ], int B[ ], int C[ ], int N ) { Problem: Move all 1 plates to either B or C, if( N == ) { B[0] from = A[0] A ; return ; } if( Ntimes == 2 ) {smaller C[0] = A[0] ; such that at all plates are on top of A[0] = B[0] ; C[0] = B[0] ; return ; } larger plates. Hanoi ( A, C, B, N-1 ) ; Hanoi ( &A[N-1], &B[N-1], C, 1 ) ; Hanoi ( C, B, A, N-1 ) ; return ; } A B C

Most people are able to grasp the sequence of movements to solve the Towers of Hanoi problem. Towers of Hanoi Problem: all plates from to eitherbase B orcases C, of The solution is. Move recursive, built up from. Ahandling such that at all times plates are on topit of N=1, 2 and 3 plates. Once smaller the pattern is understood, is then larger plates. reapplied to arbitrary N. DONEis much !! harder, however. Programming an iterative!!algorithm ( Try it – but in your spare time : ) A B C

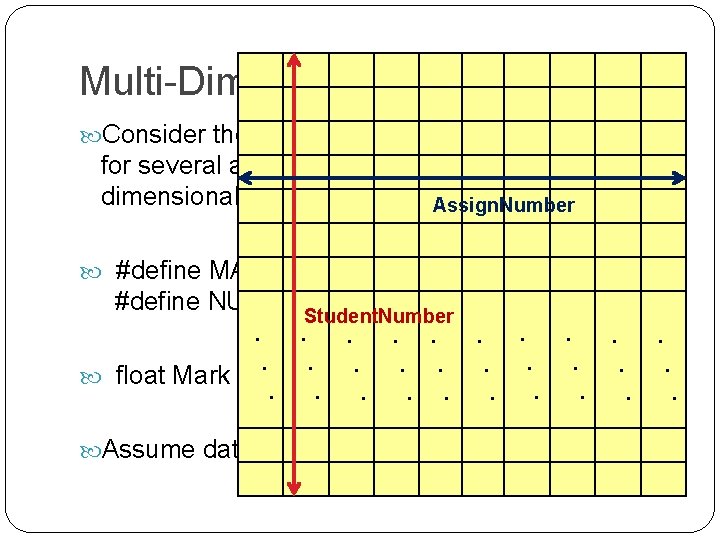
Multi-Dimensional Arrays Consider the case of student marks (0. 0 to 10. 0) for several assignments, all stored in a 2 dimensional array of float values Assign. Number #define MAX_STUDS 120 #define NUM_ASSIGNS 10 Student. Number. . . float Mark [ MAX_STUDS ] [ NUM_ASSIGNS ] ; . . . . Assume data is in a file called In. Data. dat

Multi-Dimensional Arrays We assume that the input file In. Data. dat has been prepared as follows: The file may be empty, in which case the end-of-file indicator can be checked using EOF Assign. Number A non-empty file contains (at the least) One line containing two integer values greater or equal to zero These correspond to the number of students and number of assignments, respectively The rest of the file contains Student. Number . by. . . followed. an integer, . . Number, . the Student. A line containing . . . The. number. . point. values. . of. . as floating A line containing. the marks corresponds. . number. specified. . to the. of assignments. . . The file terminates when the end-of-file indicator arises and is checked using EOF. Marks must be inserted according to the Student Number value (in the range from 0 to MAX_STUDS-1)

Multi-Dimensional Arrays /* Input from In. Data. dat using input redirection cmdprompt: >a. out < In. Data. dat */ #define MAX_STUDS 120 #define NUM_ASSIGNS 10 float Mark [ MAX_STUDS ] [ NUM_ASSIGNS ] ; int Number. Students, Number. Assignments, Stud. Num ; int S, A ; /* Utility integers */ /* Test input file for data */ if( (A=scanf( “%d%d”, &Number. Students, &Number. Assignments )) == EOF ) return 0 ; /* Data exists, so input data until EOF is encountered */ for( S=0 ; S < Number. Students ; S++ ) { if ( (A=scanf( “%d”, &Stud. Num )) == EOF ) break; /* A record exists so input assignment marks */ for( A=0 ; A < Number. Assignments ; A++ ) scanf( “%f”, &Mark[ Stud. Num ][A] ) ; }

Multi-Dimensional Arrays N-D Arrays as function arguments Unlike 1 -D arrays, all array maximum dimensions must be declared explicitly (except for the leftmost dimension) Example – Input. Marks( NS, NA, Mark ) Prototype void Input. Marks( int, float [][NUM_ASSIGNS] ) ; Function Definition void Input. Marks( int NS, int NA, float M[][NUM_ASSIGNS] ) { /* variable def’ns, logic */ return ; }

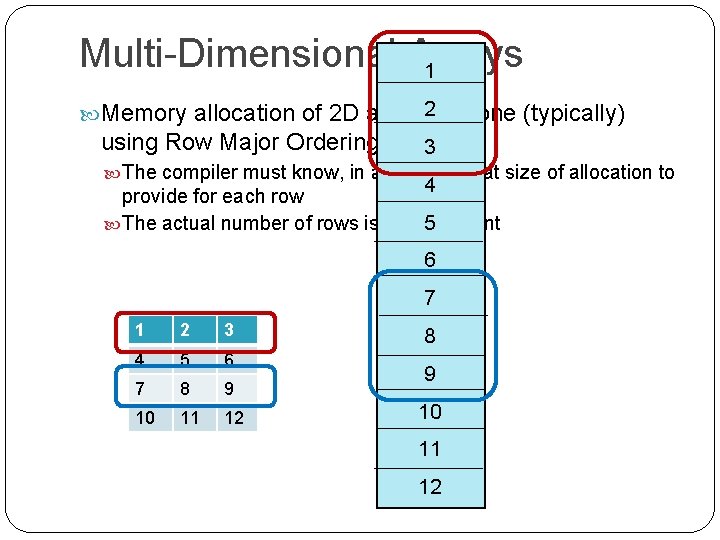
Multi-Dimensional Arrays 1 Memory allocation of 2 D arrays 2 is done (typically) using Row Major Ordering. 3 The compiler must know, in advance, what size of allocation to 4 provide for each row 5 The actual number of rows is not important 6 7 1 2 3 4 5 6 7 8 9 10 11 12

Multi-Dimensional Arrays Memory allocation of 2 D arrays is done (typically) Row Major Ordering. Higherusing dimensional arrays must specify all lower dimensions The compiler must know, inonly advance, what sizedimension of allocation to maximum values, leaving the highest provide for each row unspecified. The actual number of rows is not important void Input. Marks( int, float [] [NUM_ASSIGNS] ) ; Example prototype statement for a 3 D array: The compiler replaces subscript references by Base address pointer plus relative offset int Func( int Array [ ] [ MAX_ROW ] [ MAX_COL ], The Base address is just the address of the first element in the int&A[0][0] Page, int Row, int Col ) ; 2 D array, or The relative offset is given by The allocation is understood in terms+of Page* sizeof Major Rowsub * ( #Columns * sizeof elementtype) Colsub elementtype Rowsub * ( which #Columns * sizeof that elementtype) + Colsub * sizeof elementtype Ordering requires the compiler know MAX_ROW and MAX_COL in advance. To compute this expression requires the #Columns

Multi-Dimensional Arrays Working with 2 -D arrays necessitates thought and care about the operations to be performed on them and how they are defined and referenced Matrix Transpose - Transpose( A, AT, NR, NC ) Interchange rows and columns Prototype: void Transpose( float [ ] [MC], float [ ] [MR], int ) ; The result array must be defined to be of suitable size If we define: then we must define: float A [MR] [MC]; float AT [MC] [MR]; Key statement for( r=0; r<NR ; r++ ) for( c=0; c<NC ; c++ ) AT[ c ][ r ] = A[ r ][ c ] ;

Multi-Dimensional Arrays Working with 2 -D arrays necessitates thought and care about the operations to be performed on them and how they are defined and referenced Sorting - Sort( A, NR, NC ) When swapping rows, make sure to swap every element in corresponding columns Assume sorting on the first column, in ascending order Key statement (assume r 1 < r 2) if( A[ r 1 ][ 0 ] > A[ r 2 ][ 0 ] ) for( c=0 ; c<NC ; c++) fswap( &A[ r 1 ][ c ] , &A[ r 2 ][ c ] );

2 D Arrays and Graphics The layout of most computer monitors (ie. screens) is pixel based, with chemical “dots” at fixed locations on a 2 D grid, with rows and columns. Images can be broken down into 2 D array sections (eg. rectangles, circles) and colours assigned to each position PIXEL These correspond to pixel locations Drawing of images involves algorithms that work with data in 2 D arrays. Lines, Rectangles, Ellipses Lighting and Shading Projection of 3 D structures onto a 2 D plane Software libraries are very useful, but programmers must understand the basic mathematical operations underlying the algorithms Linear algebra, Calculus

Summary Concepts & Mechanisms Searching Sorting

Topic Summary Concepts & Mechanisms Algorithms Searching Sorting Reading – Chapter 6 , 7. 1 – 7. 4 One- and multi-dimensional arrays Pointers, call-by-value and call-by-reference