Aritmetic Index Page 2 Page 4 Page 6




























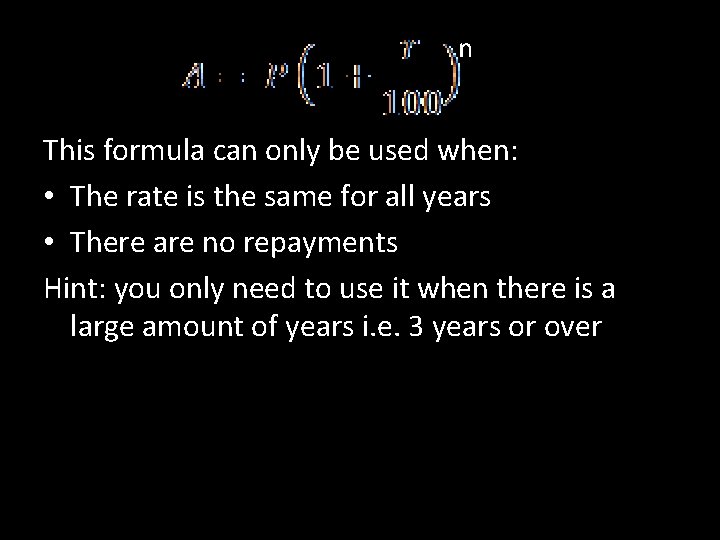








- Slides: 42

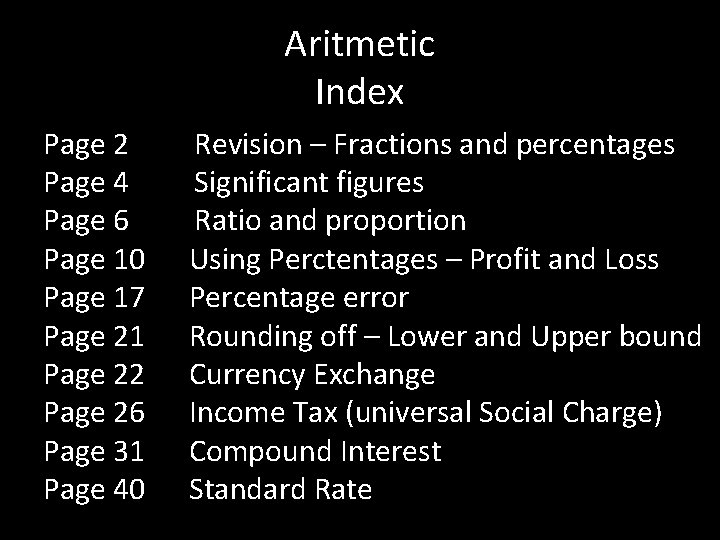
Aritmetic Index Page 2 Page 4 Page 6 Page 10 Page 17 Page 21 Page 22 Page 26 Page 31 Page 40 Revision – Fractions and percentages Significant figures Ratio and proportion Using Perctentages – Profit and Loss Percentage error Rounding off – Lower and Upper bound Currency Exchange Income Tax (universal Social Charge) Compound Interest Standard Rate

Arithmetic Revision from 1 st year Fractions and Decimals – Rounding off Express the following as a fraction in its simplest form: (i) 12 as a fraction of 75 ¹²⁄₇₅ = ⁴⁄₂₅ (ii) 55 c as a fraction of € 3. 20 = ⁵⁵⁄₃₂₀ = ¹¹⁄₆₄ (iii) 1/2 km as a fraction of 4. 5 km = ⁵⁰⁰⁄₄₅₀₀ = ¹⁄₉ (iv) The boys in the class as a fraction of the whole class. . .

Percentages Express the following as a percentages (i) 12 as a fraction of 75 ¹²⁄₇₅ = ⁴⁄₂₅ x ¹⁰⁰⁄₁= 16% (ii) 55 c as a fraction of € 3. 20 = ⁵⁵⁄₃₂₀ = ¹¹⁄₆₄x ¹⁰⁰⁄₁ = 17. 19% (iii) 1/2 km as a fraction of 4. 5 km = ⁵⁰⁰⁄₄₅₀₀ = ¹⁄₉x ¹⁰⁰⁄₁= 17. 19% (iv) The boys in the class as a fraction of the whole class. . .

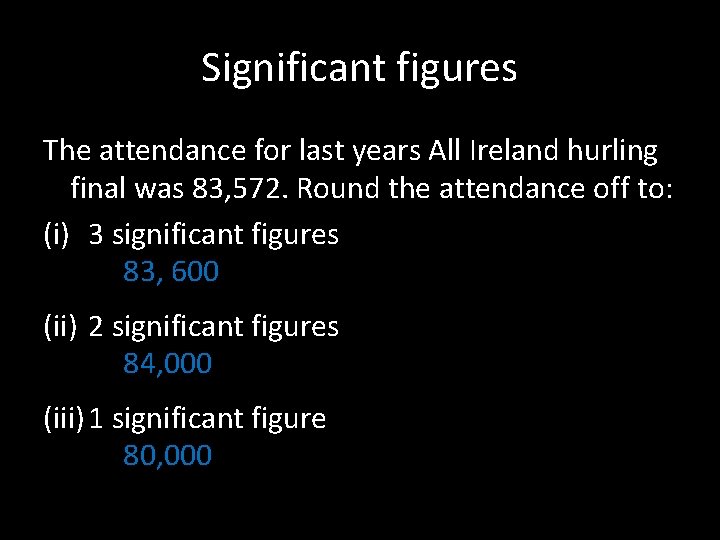
Significant figures The attendance for last years All Ireland hurling final was 83, 572. Round the attendance off to: (i) 3 significant figures 83, 600 (ii) 2 significant figures 84, 000 (iii) 1 significant figure 80, 000

Significant Figures Decimals A grain of salt measured on an extremely sensitive scale came out as 0. 0079381 milligrams Round this off to: (i) 3 signficant figures 0. 00794 mg (ii) 2 significant figures 0. 0079 mg (iii) 1 significant figure 0. 008 mg

Ratio and Proportion 1. A sum of € 420 is divided between 3 people in a ratio of 1: 2: 4. Find how much each person gets. 2. sum of money is divided between Daniel, Michael and Elaine in the ratio 2: 4: 5. If Michael got € 36, find the sum of money and how much Daniel and Elaine received.

A sum of € 420 is divided between 3 people in a ratio of 1: 2: 4. Find how much each person gets. Divide 420 in a ratio of 1: 2: 4 Add 1 + 2 + 4 = 7 There are seven shares altogether. 420 ÷ 7 = 60 60 x 1 = 60 60 x 2 = 120 60: 120: 240 60 x 4 = 240

A sum of money is divided between Daniel, Michael and Elaine in the ratio 2: 4: 5. If Michael got € 56, find the total sum of money and how much Daniel and Elaine received. If Michael got 4 out of 11 shares, we see how much 1 share is: 56 ÷ 4 = `€ 14 (1 share) There are 11 shares altogether. . . 1 share = € 14 11 shares = € 154 (14 x 11) Elaine received 14 x 5 = € 70 Daniel received 14 x 2 = € 28

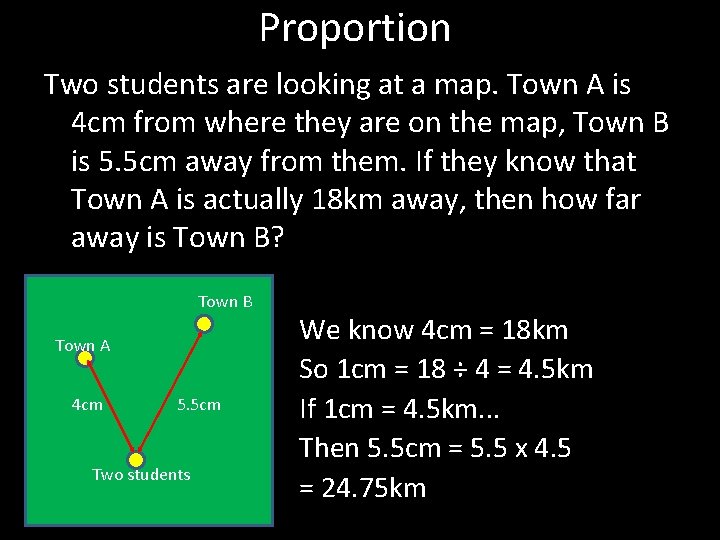
Proportion Two students are looking at a map. Town A is 4 cm from where they are on the map, Town B is 5. 5 cm away from them. If they know that Town A is actually 18 km away, then how far away is Town B? Town B Town A 4 cm 5. 5 cm Two students We know 4 cm = 18 km So 1 cm = 18 ÷ 4 = 4. 5 km If 1 cm = 4. 5 km. . . Then 5. 5 cm = 5. 5 x 4. 5 = 24. 75 km

Using Percentages Find 21. 4% of € 530 3 ways of doing it: 1. Multiply 530 x 21. 4 then divide by 100 2. Multiply 530 x 0. 214 3. Multiply 530 x 21. 4% using calculator Answer: € 113. 42

Other uses (i) 23% of a certain amount of money works out as € 248. 40. Find the original sum? (ii) VAT of 21% is added to the cost of a bag. If the price after VAT is € 107. 69, find the original cost

23% of a certain amount of money works out as € 248. 40. Find the original sum? We approach this by first finding 1% If 23% = 248. 40 then 1% = 248. 40 ÷ 23 1% = € 10. 80 100% = € 1080

VAT of 21% is added to the cost of a bag. If the price after VAT is € 107. 69, find the original cost We always take the original sum as 100% When we add 21% onto the original price, the new price is the same as 121% = € 107. 69 1% = 0. 89 100% = € 89

Profit and Loss % Profit = profit Cost Price X 100 1 A company buys shares at a € 3. 20 per share. They then sell it at a price of € 3. 90 per share. What was their % profit? John loses his phone so buys a new one for € 79. He then finds his old phone so he sells the new one for € 60. What is the % loss he makes on the phone?

A company buys shares at a € 3. 20 per share. They then sell it at a price of € 3. 90 per share. What was their % profit? % Profit = = profit Cost Price X 0. 7 3. 20 x = 21. 875% 100 1

John buys a loses his phone so buys a new one for € 79. He then finds his old phone so he sells the new one for € 60. What is the % loss he makes on the phone? % Profit = 100 In this case John makes a loss. The formula is the same. loss X Cost Price = 19 60 1 X 100 1 = 31. 67% (Loss)

% Error Estimate the area of the garden. Answer using Trapezoidal Rule: 180 cm³ It was calculated that the actual are was 183. 57 cm³. Calculate the % error to two decimal places % error = error x 100 true value 1 = 3. 57/183. 57 x 100/1 = 1. 94%

Question 7 and 8 (page 112) Estimate: 150 cm² Actual Area = πr² = (²²⁄₇)(7)² = 154 cm² Error: 4 cm² % error = error x 100 true value 1 % error = 4 x 100 154 1 % Error = 2. 6%

Q 8 To change Celcius to Farenheit we use the formula F = ⁹⁄₅C + 32 (i) if it’s 20⁰ then: F = ⁹⁄₅(20) + 32 Correct value for F = 68⁰F (ii) Estimate = 2(15 + 20) % error = error true value = 70⁰F % error = 2 68 Error = 2⁰F x % Error = 2. 9% 100 1 x 100 1

Exercise Q 9, 10, 11

Rounding Off A man measures the length of a hallway and rounds it off to the nearest metre. He deduced that the hall was 8 metres long. What is the maximum and minimum length the hall could have been to the nearest centimetre? If he measured the hall to be 8. 49 metres, then he would have rounded it to 8 metres. If he measured the hall to be 7. 50 metres he would have rounded up to 8 metres also. 7. 50 is called the LOWER BOUND and 77. 49 is called the UPPER BOUND

Currency Transactions (i) A tourist is travelling from America to Ireland. He calculates he will need about € 1300 spending money. If the exchange rate is € 1 : $1. 15, calculate how many dollars he needs to exchange. (ii) He returns home after the holiday and changed his left over euro back into dollars. If he had $160 left over, calculate in euros how much he spent on his holiday. (Round off to the nearest euro)

A tourist is travelling from America to Ireland. He calculates he will need about € 1300 spending money. If the exchange rate is € 1 : $1. 15, calculate how many dollars he needs to exchange. € 1300 to dollars: Exchange rate € 1 : $1. 15 1300 x 1. 15 = $1495

He returns home after the holiday and changed his left over euro back into dollars. If he had $160 left over, calculate in euros how much he spent on his holiday How much euro had he left over? Exchange rate € 1 : $1. 15 $160 ÷ 1. 15 = € 139 Total spent = 1300 – 139 = € 1161

Recap It’s either going to be multiply or divide by exchange rate € 1 : $1. 15 Dollars are bigger than euro therefore the answer will be the same € 1300 = $1495

Q 4 page 114 € 1 = $1. 4 € 1 = Y 112 (i) Euro to Dollars are bigger, so multiply € 1200 = 1200 x 1. 4 = $1680 (ii) € 2400 x 112 = Y 268, 800 (iii) Euro to Franc Euro is smaller so divide 4500 ÷ 1. 32 = 3409 € 1 = F 1. 32

Ctd. . . € 1 = $1. 4 € 1 = Y 112 € 1 = F 1. 32 (iv) $1350 = 1350 ÷ 1. 4 = € 964. 29 (v) Ratio is $1. 4 = Y 112 $1 = Y 80 Y 36000 = 36000 ÷ 80 = € 450 (vi) Ratio Y 112 = F 1. 32 = Y 84. 84 = F 1 F 7500 = 7500 x 84. 84 = Y 636363. 64

Q 5 Annual Salary € 45, 000 Standard Rate (€ 31, 000 x 20%) Higher Rate (€ 14, 000 x 45%) Gross Tax Less Tax Credits Total Tax Payable € 6, 200 € 6, 300 € 12, 500 € 4, 650 € 7850

Q 6 Annual Salary € 43, 000 Standard Rate (€ 43, 000 x r%) Gross Tax payable Less Tax Credits Tax Payable Gross Tax = 5960 + 3500 = 9460 as a % of 43, 000 ⁹⁴⁶⁰⁄₄₃₀₀₀ x ¹⁰⁰⁄₁ =22% ? ? € 3, 500 € 5, 960

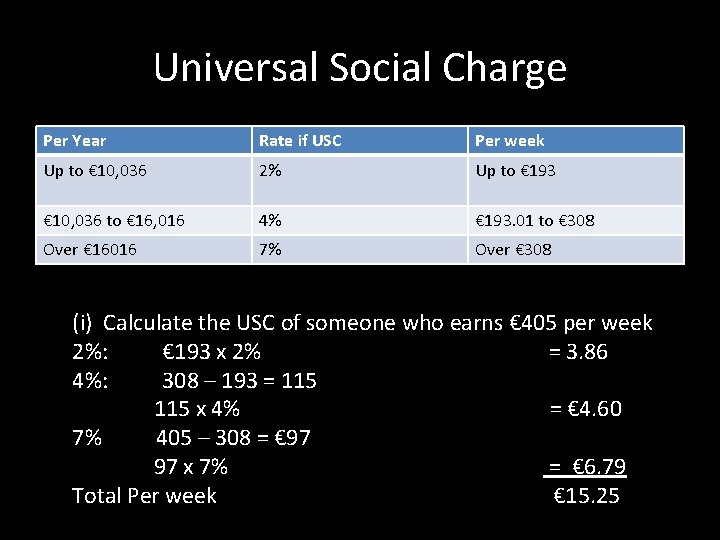
Universal Social Charge Per Year Rate if USC Per week Up to € 10, 036 2% Up to € 193 € 10, 036 to € 16, 016 4% € 193. 01 to € 308 Over € 16016 7% Over € 308 (i) Calculate the USC of someone who earns € 405 per week 2%: € 193 x 2% = 3. 86 4%: 308 – 193 = 115 x 4% = € 4. 60 7% 405 – 308 = € 97 97 x 7% = € 6. 79 Total Per week € 15. 25

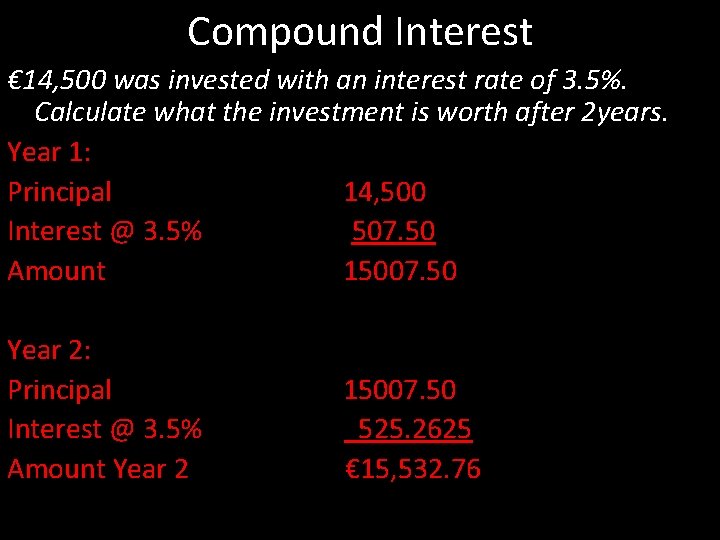
Compound Interest € 14, 500 was invested with an interest rate of 3. 5%. Calculate what the investment is worth after 2 years. Year 1: Principal 14, 500 Interest @ 3. 5% 507. 50 Amount 15007. 50 Year 2: Principal Interest @ 3. 5% Amount Year 2 15007. 50 525. 2625 € 15, 532. 76

Formula Principal (P) – Money invested/borrowed Amount (A) – Money at end of investment Rate (r) – percentage interest Formula: n Example: (i) Find the amount 11, 200 increases to after being invested for 5 years at a rate of 4% (ii) How much interest did it gain? (i)A = 11, 200(1 + ⁴⁄₁₀₀)⁵ A = 11, 200(1¹⁄₂₅)⁵ A = 11, 200(1. 21665) A = € 13, 626. 51

n Example: (i) Find the amount 11, 200 increases to after being invested for 5 years at a rate of 4% (ii) How much interest did it gain? (i)A = 11, 200(1 + ⁴⁄₁₀₀)⁵ A = 11, 200(1¹⁄₂₅)⁵ A = 11, 200(1. 21665) A = € 13, 626. 51 (ii) Principal = € 11, 200 Amount = € 13, 626. 51 Interest gained = 13, 626. 51 - 11, 200 = € 2, 426. 51
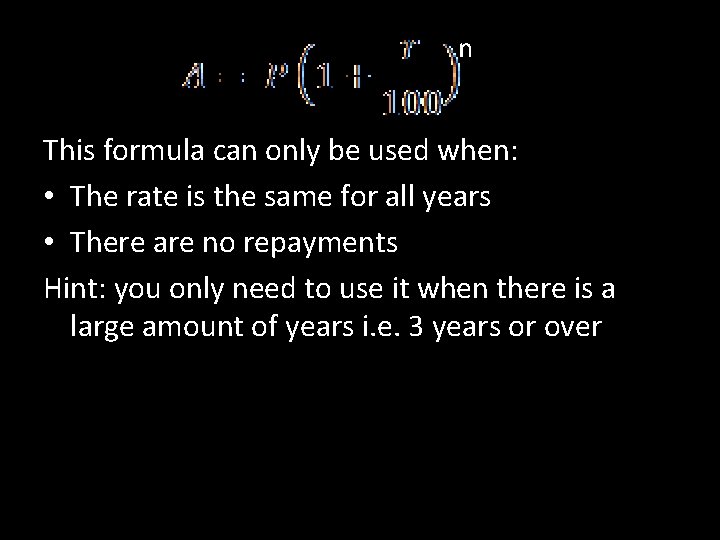
n This formula can only be used when: • The rate is the same for all years • There are no repayments Hint: you only need to use it when there is a large amount of years i. e. 3 years or over

Q 15 page 124 A sum of money is invested at r% amounts to € 5175 after one year and € 5951. 25 after 2 years. Find (i) the value of r (ii)the sum invested General Structure Year 1 Principal Interest @ 15% Amount Y 1 Year 2 Principal Y 2 Interest @15% Amount Y 2 ⁷⁷⁶∙²⁵⁄₅₁₇₅ x ¹⁰⁰⁄₁ = 15% € 4, 500 € 5175 € 776. 25 € 5951. 25 € 5175 = 115% 1% = 45 100% = € 4, 500

Overall Equivelance Rate A bank offers 5% annual interest on investments if they invest for 8 years. Calculate the overall % rate of interest for the 8 years. We want to calculate what % interest the investment earns after 8 years n A = 100(1+⁵⁄₁₀₀)⁸ A = 147. 75 Interest = 147. 75 – 100 =47. 75 Overall % Rate = 47. 75%

A bank charges 30% from a loan after 6 years. Calculate the annual equivalence rate i. e. What is the interest rate per year. Make the PRINCIPAL € 100. After 6 years, the AMOUNT will be € 130 n 130 = 100(1+ r/100)⁶ (1 + r/100)⁶ = 1. 3 1 + r/100 = ⁶√ 1. 3 1 + r/100 = 1. 044 r = 4. 47%

Q 16 An investment bond gives 25% after 5 years Calculate the AER for the bond. Principal = € 100 Amount = € 125 r=? n 125 = 100(1 + r/100)⁵ 1. 25 = (1 + r/100)⁵ ⁵√ 1. 25 = 1 + r/100 1. 0456 = 1 + r/100 = 0. 0456 r = 4. 6%

Q 17 A credit card charges a rate of 2. 5% per month, calculate the AER P = 100 A=? r = 2. 5% n = 12 n A = 100(1 + ²˙⁵⁄₁₀₀)¹² A = 134. 49 Interest Earned in 1 year = 34. 49 AER = € 34. 5%

Standard Form Distance from Earth to the moon is 357, 000 km Distance from Earth to the Sun is 149, 597, 881. 5 km The nearest star to Earth is approx. 42, 000, 000 km To turn that into standard form: 4. 2 x 10¹⁶ Has to be a number between 1 -10

Other way around If we take the number 0. 000000054 How many steps do we move the decimal place? 5. 4 x 10⁸ 1. Change the following to standard form (i) 4, 500, 000 (ii) 60, 000 (iii)0. 00083 (iv) 0. 0032 -4 -3 6 x 10⁴ 8. 3 x 10 3. 2 x 10 4. 5 x 10⁶ 2. Change the following to a decimal number (i) 3. 5 x 10⁵ (ii) 3. 9 x 10 -⁶ (iii) 4. 89 x 10⁷ (iv) 3. 5 x 10² 350, 000 48, 900, 000 0. 0000039 350
